Direct and Inverse Problems for Models with Uncertain Data Modelling real-world physical systems always includes uncertainties (at least implicitly) regarding the measurement and determination of the data of the model. This for instance involves material properties, loading and also domains. We are concerned with infinite dimensional space dependent systems which are described by PDEs. Typical applications are the simulation of mechanical systems and of groundwater flow in porous media. Since the solutions directly depend on the data, the measurement of this dependence in probabilistic terms is required in order to asses the reliability of the calculated solution. By this, it becomes feasible to deduce and quantify the solution statistics depending on data uncertainties.
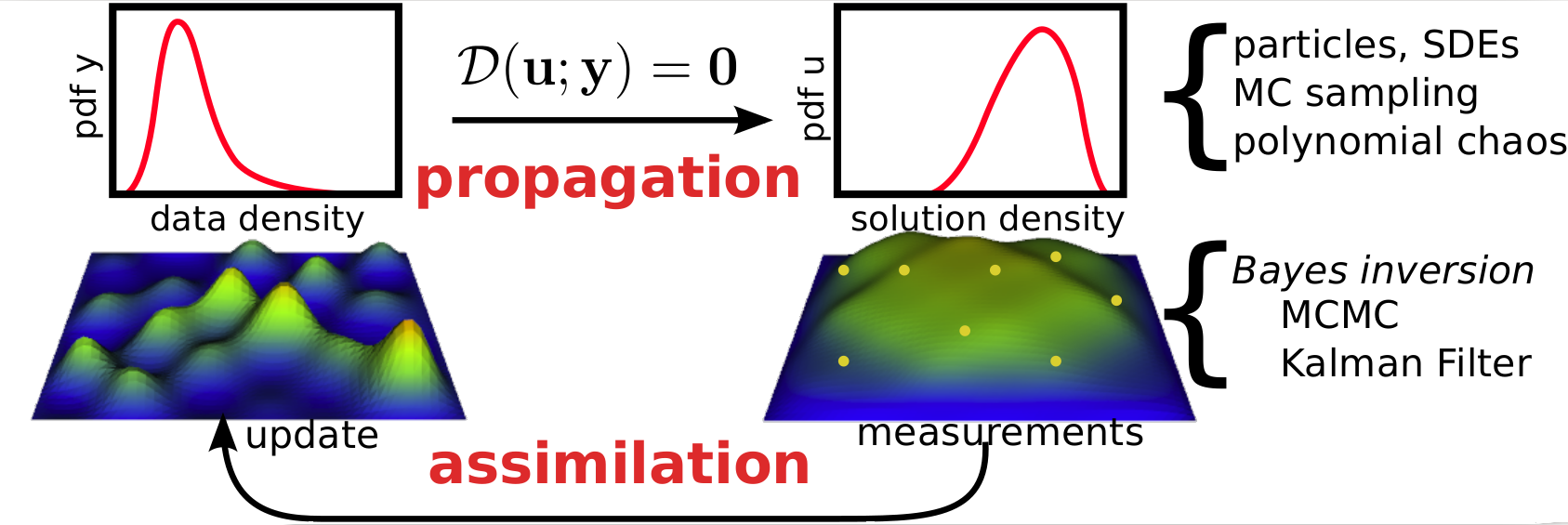
Illustration of forward propagation of uncertainties and inverse parameter identification.
The numerical treatment of these problems usually requires a computational effort which is significantly larger than for deterministic problems and which may easily become intractable computationally. Thus, the development and analysis of efficient model reduction techniques for the numerical evaluation is important to enable the treatment of relevant applications. Depending on the data model, we employ modern sampling methods (multilevel Monte-Carlo) as well as projection methods based on the polynomial chaos (stochastic collocation and stochastic FEM). Depending on the chosen problem and data model, different methods are employed which either perform a discretization of the function space or determine statistics of functionals based on samples. In particular, these are - projection methods based on polynomial chaos (stochastic Galerkin FEM and sparse regression)
- modern sampling methods (multilevel and Quasi Monte Carlo)
- methods based on stochastic differential equations (SDEs)
Adaptive Functional Representations and Modern Compression Techniques

Illustration of forward propagation of uncertainties and inverse parameter identification.
The evaluation of forward or inverse stochastic problems often can be accellerated significantly (in terms of convergence rates) by employing functional representations. Moreover, such a representation allows for a numerical analysis, which resembles and extends concepts known from deterministic PDEs. With discretizations in generalized polynomial chaos as e.g. used for stochastic Galerkin methods, (reliable) a posteriori error estimates can be computed. These iteratively lead to problem-adapted solution spaces with optimal convergence.
Since the discrete algebraic systems exhibit a high dimensionality, model reduction techniques are often inevitable. Apart from the adaptation of the discrete space, we employ modern hierarchical tensor methods for the compression of the operators and the parametric solutions. This is tightly related to a possible representation as low-rank manifold. The tensor train (TT) format has proven advantageous for this.Applications for the developed methods can e.g. be found with sampling-free Bayesian inversion, topology optimization under uncertainties, and the determination of effective material models in case of media with multiscale properties.
Mesh adaptivity with oscillating coefficient field.
SDE- and Sampling-based Methods for Random PDEs
As an alternative to Monte Carlo methods, we investigate methods which exploit the equivalence of PDEs with random data and stochastic differential equations (Feynman-Kac). Such highly parallelizable approaches typically require the reconstruction of a global solution representation. However, they allow for a complete separate and local control of all discretization parameters. To be more specific, pointwise solution realizations in the physical domain are determined by some appropriate numerical method (Euler-Maruyama). Subsequently these are either used for a global or local polynomial regression or an interpolation on a mesh.
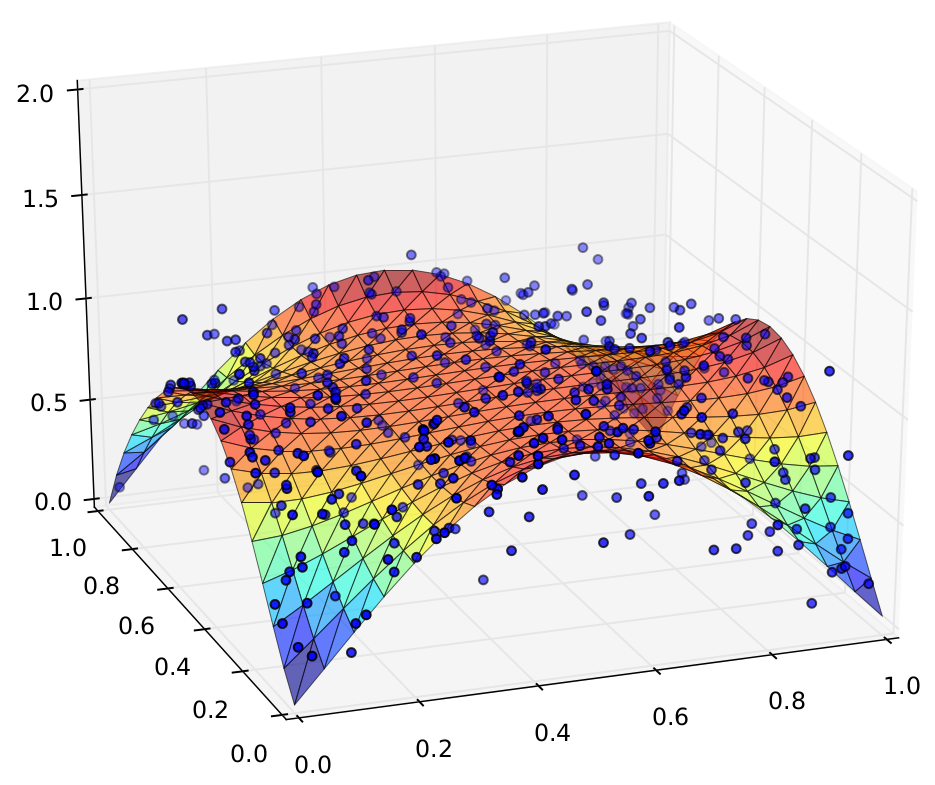
Regression approach for the pointwise solution of an SDE equivalent to the random PDE.
Publications
 Monographs
Monographs
-
M. Eigel, Ch. Merdon, Chapter Eight --- A posteriori error control for stochastic Galerkin FEM with high-dimensional random parametric PDEs, F. Chouly, S.P.A. Bordas, R. Becker, P. Omnes, eds., 60 of Advances in Applied Mechanics, Elsevier, 2025, pp. 347--397, (Chapter Published), DOI 10.1016/bs.aams.2025.02.008 .
-
P. Deuflhard, M. Grötschel, D. Hömberg, U. Horst, J. Kramer, V. Mehrmann, K. Polthier, F. Schmidt, Ch. Schütte, M. Skutella, J. Sprekels, eds., MATHEON -- Mathematics for Key Technologies, 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, 453 pages, (Collection Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
M. Bachmayr, M. Eigel, H. Eisenmann, I. Voulis, A convergent adaptive finite element stochastic Galerkin method based on multilevel expansions of random fields, SIAM Journal on Numerical Analysis, 63 (2025), pp. 1776--1807, DOI 10.1137/24M1649253 .
Abstract
The subject of this work is an adaptive stochastic Galerkin finite element method for parametric or random elliptic partial differential equations, which generates sparse product polynomial expansions with respect to the parametric variables of solutions. For the corresponding spatial approximations, an independently refined finite element mesh is used for each polynomial coefficient. The method relies on multilevel expansions of input random fields and achieves error reduction with uniform rate. In particular, the saturation property for the refinement process is ensured by the algorithm. The results are illustrated by numerical experiments, including cases with random fields of low regularity. -
M. Drieschner, R. Gruhlke, Y. Petryna, M. Eigel, D. Hömberg, Local surrogate responses in the Schwarz alternating method for elastic problems on random voided domains, Computer Methods in Applied Mechanics and Engineering, 405 (2023), pp. 115858/1--115858/18, DOI 10.1016/j.cma.2022.115858 .
Abstract
Imperfections and inaccuracies in real technical products often influence the mechanical behavior and the overall structural reliability. The prediction of real stress states and possibly resulting failure mechanisms is essential and a real challenge, e.g. in the design process. In this contribution, imperfections in elastic materials such as air voids in adhesive bonds between fiber-reinforced composites are investigated. They are modeled as arbitrarily shaped and positioned. The focus is on local displacement values as well as on associated stress concentrations caused by the imperfections. For this purpose, the resulting complex random one-scale finite element model is numerically solved by a new developed surrogate model using an overlapping domain decomposition scheme based on Schwarz alternating method. Here, the actual response of local subproblems associated with isolated material imperfections is determined by a single appropriate surrogate model, that allows for an accelerated propagation of randomness. The efficiency of the method is demonstrated for imperfections with elliptical and ellipsoidal shape in 2D and 3D and extended to arbitrarily shaped voids. For the latter one, a local surrogate model based on artificial neural networks (ANN) is constructed. Finally, a comparison to experimental results validates the numerical predictions for a real engineering problem. -
C. Heiss, I. Gühring, M. Eigel, Multilevel CNNs for parametric PDEs, Journal of Machine Learning Research (JMLR). MIT Press, Cambridge, MA. English, English abstracts., 24 (2023), pp. 373/1--373/42.
Abstract
We combine concepts from multilevel solvers for partial differential equations (PDEs) with neural network based deep learning and propose a new methodology for the efficient numerical solution of high-dimensional parametric PDEs. An in-depth theoretical analysis shows that the proposed architecture is able to approximate multigrid V-cycles to arbitrary precision with the number of weights only depending logarithmically on the resolution of the finest mesh. As a consequence, approximation bounds for the solution of parametric PDEs by neural networks that are independent on the (stochastic) parameter dimension can be derived.The performance of the proposed method is illustrated on high-dimensional parametric linear elliptic PDEs that are common benchmark problems in uncertainty quantification. We find substantial improvements over state-of-the-art deep learning-based solvers. As particularly challenging examples, random conductivity with high-dimensional non-affine Gaussian fields in 100 parameter dimensions and a random cookie problem are examined. Due to the multilevel structure of our method, the amount of training samples can be reduced on finer levels, hence significantly lowering the generation time for training data and the training time of our method.
-
M. Eigel, N. Farchmin, S. Heidenreich, P. Trunschke, Adaptive nonintrusive reconstruction of solutions to high-dimensional parametric PDEs, SIAM Journal on Scientific Computing, 45 (2023), pp. A457--A479, DOI 10.1137/21M1461988 .
Abstract
Numerical methods for random parametric PDEs can greatly benefit from adaptive refinement schemes, in particular when functional approximations are computed as in stochastic Galerkin and stochastic collocations methods. This work is concerned with a non-intrusive generalization of the adaptive Galerkin FEM with residual based error estimation. It combines the non-intrusive character of a randomized least-squares method with the a posteriori error analysis of stochastic Galerkin methods. The proposed approach uses the Variational Monte Carlo method to obtain a quasi-optimal low-rank approximation of the Galerkin projection in a highly efficient hierarchical tensor format. We derive an adaptive refinement algorithm which is steered by a reliable error estimator. Opposite to stochastic Galerkin methods, the approach is easily applicable to a wide range of problems, enabling a fully automated adjustment of all discretization parameters. Benchmark examples with affine and (unbounded) lognormal coefficient fields illustrate the performance of the non-intrusive adaptive algorithm, showing best-in-class performance. -
M. Eigel, N. Farchmin, S. Heidenreich, P. Trunschke, Efficient approximation of high-dimensional exponentials by tensor networks, International Journal for Uncertainty Quantification, 13 (2023), pp. 25--51, DOI 10.1615/Int.J.UncertaintyQuantification.2022039164 .
Abstract
In this work a general approach to compute a compressed representation of the exponential exp(h) of a high-dimensional function h is presented. Such exponential functions play an important role in several problems in Uncertainty Quantification, e.g. the approximation of log-normal random fields or the evaluation of Bayesian posterior measures. Usually, these high-dimensional objects are intractable numerically and can only be accessed pointwise in sampling methods. In contrast, the proposed method constructs a functional representation of the exponential by exploiting its nature as a solution of an ordinary differential equation. The application of a Petrov--Galerkin scheme to this equation provides a tensor train representation of the solution for which we derive an efficient and reliable a posteriori error estimator. Numerical experiments with a log-normal random field and a Bayesian likelihood illustrate the performance of the approach in comparison to other recent low-rank representations for the respective applications. Although the present work considers only a specific differential equation, the presented method can be applied in a more general setting. We show that the composition of a generic holonomic function and a high-dimensional function corresponds to a differential equation that can be used in our method. Moreover, the differential equation can be modified to adapt the norm in the a posteriori error estimates to the problem at hand. -
M. Eigel, R. Gruhlke, D. Moser, Numerical upscaling of parametric microstructures in a possibilistic uncertainty framework with tensor trains, Computational Mechanics, 71 (2023), pp. 615--636 (published online on 27.12.2022), DOI 10.1007/s00466-022-02261-z .
Abstract
We develop a new fuzzy arithmetic framework for efficient possibilistic uncertainty quantification. The considered application is an edge detection task with the goal to identify interfaces of blurred images. In our case, these represent realisations of composite materials with possibly very many inclusions. The proposed algorithm can be seen as computational homogenisation and results in a parameter dependent representation of composite structures. For this, many samples for a linear elasticity problem have to be computed, which is significantly sped up by a highly accurate low-rank tensor surrogate. To ensure the continuity of the underlying effective material tensor map, an appropriate diffeomorphism is constructed to generate a family of meshes reflecting the possible material realisations. In the application, the uncertainty model is propagated through distance maps with respect to consecutive symmetry class tensors. Additionally, the efficacy of the best/worst estimate analysis of the homogenisation map as a bound to the average displacement for chessboard like matrix composites with arbitrary star-shaped inclusions is demonstrated. -
M. Eigel, R. Gruhlke, M. Marschall, Low-rank tensor reconstruction of concentrated densities with application to Bayesian inversion, Statistics and Computing, 32 (2022), pp. 27/1--27/27, DOI 10.1007/s11222-022-10087-1 .
Abstract
A novel method for the accurate functional approximation of possibly highly concentrated probability densities is developed. It is based on the combination of several modern techniques such as transport maps and nonintrusive reconstructions of low-rank tensor representations. The central idea is to carry out computations for statistical quantities of interest such as moments with a convenient reference measure which is approximated by an numerical transport, leading to a perturbed prior. Subsequently, a coordinate transformation leads to a beneficial setting for the further function approximation. An efficient layer based transport construction is realized by using the Variational Monte Carlo (VMC) method. The convergence analysis covers all terms introduced by the different (deterministic and statistical) approximations in the Hellinger distance and the Kullback-Leibler divergence. Important applications are presented and in particular the context of Bayesian inverse problems is illuminated which is a central motivation for the developed approach. Several numerical examples illustrate the efficacy with densities of different complexity. -
M. Eigel, O. Ernst, B. Sprungk, L. Tamellini, On the convergence of adaptive stochastic collocation for elliptic partial differential equations with affine diffusion, SIAM Journal on Numerical Analysis, 60 (2022), pp. 659--687, DOI 10.1137/20M1364722 .
Abstract
Convergence of an adaptive collocation method for the stationary parametric diffusion equation with finite-dimensional affine coefficient is shown. The adaptive algorithm relies on a recently introduced residual-based reliable a posteriori error estimator. For the convergence proof, a strategy recently used for a stochastic Galerkin method with an hierarchical error estimator is transferred to the collocation setting. -
M. Eigel, M. Haase, J. Neumann, Topology optimisation under uncertainties with neural networks, Algorithms, 15 (2022), pp. 241/1--241/34, DOI https://doi.org/10.3390/a15070241 .
-
M. Hintermüller, S.-M. Stengl, Th.M. Surowiec, Uncertainty quantification in image segmentation using the Ambrosio--Tortorelli approximation of the Mumford--Shah energy, Journal of Mathematical Imaging and Vision, 63 (2021), pp. 1095--1117, DOI 10.1007/s10851-021-01034-2 .
Abstract
The quantification of uncertainties in image segmentation based on the Mumford-Shah model is studied. The aim is to address the error propagation of noise and other error types in the original image to the restoration result and especially the reconstructed edges (sharp image contrasts). Analytically, we rely on the Ambrosio-Tortorelli approximation and discuss the existence of measurable selections of its solutions as well as sampling-based methods and the limitations of other popular methods. Numerical examples illustrate the theoretical findings. -
M. Drieschner, M. Eigel, R. Gruhlke, D. Hömberg, Y. Petryna, Comparison of various uncertainty models with experimental investigations regarding the failure of plates with holes, Reliability Engineering and System Safety, 203 (2020), pp. 107106/1--107106/12, DOI 10.1016/j.ress.2020.107106 .
Abstract
Unavoidable uncertainties due to natural variability, inaccuracies, imperfections or lack of knowledge are always present in real world problems. To take them into account within a numerical simulation, the probability, possibility or fuzzy set theory as well as a combination of these are potentially usable for the description and quantification of uncertainties. In this work, different monomorphic and polymorphic uncertainty models are applied on linear elastic structures with non-periodic perforations in order to analyze the individual usefulness and expressiveness. The first principal stress is used as an indicator for structural failure which is evaluated and classified. In addition to classical sampling methods, a surrogate model based on artificial neural networks is presented. With regard to accuracy, efficiency and resulting numerical predictions, all methods are compared and assessed with respect to the added value. Real experiments of perforated plates under uniaxial tension are validated with the help of the different uncertainty models. -
CH. Bayer, D. Belomestny, M. Redmann, S. Riedel, J.G.M. Schoenmakers, Solving linear parabolic rough partial differential equations, Journal of Mathematical Analysis and Applications, 490 (2020), pp. 124236/1--124236/45, DOI 10.1016/j.jmaa.2020.124236 .
Abstract
We study linear rough partial differential equations in the setting of [Friz and Hairer, Springer, 2014, Chapter 12]. More precisely, we consider a linear parabolic partial differential equation driven by a deterministic rough path W of Hölder regularity α with ⅓ < α ≤ ½ . Based on a stochastic representation of the solution of the rough partial differential equation, we propose a regression Monte Carlo algorithm for spatio-temporal approximation of the solution. We provide a full convergence analysis of the proposed approximation method which essentially relies on the new bounds for the higher order derivatives of the solution in space. Finally, a comprehensive simulation study showing the applicability of the proposed algorithm is presented. -
G. Dong, H. Guo, Parametric polynomial preserving recovery on manifolds, SIAM Journal on Scientific Computing, 42 (2020), pp. A1885--A1912, DOI 10.1137/18M1191336 .
-
M. Eigel, M. Marschall, M. Multerer, An adaptive stochastic Galerkin tensor train discretization for randomly perturbed domains, SIAM/ASA Journal on Uncertainty Quantification, 8 (2020), pp. 1189--1214, DOI 10.1137/19M1246080 .
Abstract
A linear PDE problem for randomly perturbed domains is considered in an adaptive Galerkin framework. The perturbation of the domain's boundary is described by a vector valued random field depending on a countable number of random variables in an affine way. The corresponding Karhunen-Loeve expansion is approximated by the pivoted Cholesky decomposition based on a prescribed covariance function. The examined high-dimensional Galerkin system follows from the domain mapping approach, transferring the randomness from the domain to the diffusion coefficient and the forcing. In order to make this computationally feasible, the representation makes use of the modern tensor train format for the implicit compression of the problem. Moreover, an a posteriori error estimator is presented, which allows for the problem-dependent iterative refinement of all discretization parameters and the assessment of the achieved error reduction. The proposed approach is demonstrated in numerical benchmark problems. -
M. Eigel, M. Marschall, M. Pfeffer, R. Schneider, Adaptive stochastic Galerkin FEM for lognormal coefficients in hierarchical tensor representations, Numerische Mathematik, 145 (2020), pp. 655--692, DOI 10.1007/s00211-020-01123-1 .
Abstract
Stochastic Galerkin methods for non-affine coefficient representations are known to cause major difficulties from theoretical and numerical points of view. In this work, an adaptive Galerkin FE method for linear parametric PDEs with log-normal coefficients discretized in Hermite chaos polynomials is derived. It employs problem-adapted function spaces to ensure solvability of the variational formulation. The inherently high computational complexity of the parametric operator is made tractable by using hierarchical tensor representations. For this, a new tensor train format of the lognormal coefficient is derived and verified numerically. The central novelty is the derivation of a reliable residual-based a posteriori error estimator. This can be regarded as a unique feature of stochastic Galerkin methods. It allows for an adaptive algorithm to steer the refinements of the physical mesh and the anisotropic Wiener chaos polynomial degrees. For the evaluation of the error estimator to become feasible, a numerically efficient tensor format discretization is developed. Benchmark examples with unbounded lognormal coefficient fields illustrate the performance of the proposed Galerkin discretization and the fully adaptive algorithm. -
M. Eigel, R. Gruhlke, A local hybrid surrogate-based finite element tearing interconnecting dual-primal method for non-smooth random partial differential equations, International Journal for Numerical Methods in Engineering, 122 (2021), pp. 1001--1030 (published online on 03.11.2020), DOI 10.1002/nme.6571 .
Abstract
A domain decomposition approach exploiting the localization of random parameters in high-dimensional random PDEs is presented. For high efficiency, surrogate models in multi-element representations are computed locally when possible. This makes use of a stochastic Galerkin FETI-DP formulation of the underlying problem with localized representations of involved input random fields. The local parameter space associated to a subdomain is explored by a subdivision into regions where the parametric surrogate accuracy can be trusted and where instead Monte Carlo sampling has to be employed. A heuristic adaptive algorithm carries out a problem-dependent hp refinement in a stochastic multi-element sense, enlarging the trusted surrogate region in local parametric space as far as possible. This results in an efficient global parameter to solution sampling scheme making use of local parametric smoothness exploration in the involved surrogate construction. Adequately structured problems for this scheme occur naturally when uncertainties are defined on sub-domains, e.g. in a multi-physics setting, or when the Karhunen-Loeve expansion of a random field can be localized. The efficiency of this hybrid technique is demonstrated with numerical benchmark problems illustrating the identification of trusted (possibly higher order) surrogate regions and non-trusted sampling regions. -
I. Papaioannou, M. Daub, M. Drieschner, F. Duddeck, M. Ehre, L. Eichner, M. Eigel, M. Götz, W. Graf, L. Grasedyck, R. Gruhlke, D. Hömberg, M. Kaliske, D. Moser, Y. Petryna, D. Straub, Assessment and design of an engineering structure with polymorphic uncertainty quantification, GAMM-Mitteilungen, 42 (2019), pp. e201900009/1--e201900009/22, DOI 10.1002/gamm.201900009 .
-
D. Pivovarov, K. Willner, P. Steinmann, S. Brumme, M. Müller, T. Srisupattarawanit, G.-P. Ostermeyer, C. Henning, T. Ricken, S. Kastian, S. Reese, D. Moser, L. Grasedyck, J. Biehler, M. Pfaller, W. Wall, Th. Kolsche, O. VON Estorff, R. Gruhlke, M. Eigel, M. Ehre, I. Papaioannou, D. Straub, S. Leyendecker, Challenges of order reduction techniques for problems involving polymorphic uncertainty, GAMM-Mitteilungen, 42 (2019), pp. e201900011/1--e201900011/24.
-
M. Eigel, R. Schneider, P. Trunschke, S. Wolf, Variational Monte Carlo---Bridging concepts of machine learning and high dimensional partial differential equations, Advances in Computational Mathematics, 45 (2019), pp. 2503--2532, DOI 10.1007/s10444-019-09723-8 .
Abstract
A statistical learning approach for parametric PDEs related to Uncertainty Quantification is derived. The method is based on the minimization of an empirical risk on a selected model class and it is shown to be applicable to a broad range of problems. A general unified convergence analysis is derived, which takes into account the approximation and the statistical errors. By this, a combination of theoretical results from numerical analysis and statistics is obtained. Numerical experiments illustrate the performance of the method with the model class of hierarchical tensors. -
M. Eigel, M. Marschall, R. Schneider, Sampling-free Bayesian inversion with adaptive hierarchical tensor representations, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 34 (2018), pp. 035010/1--035010/29, DOI 10.1088/1361-6420/aaa998 .
Abstract
The statistical Bayesian approach is a natural setting to resolve the ill-posedness of inverse problems by assigning probability densities to the considered calibration parameters. Based on a parametric deterministic representation of the forward model, a sampling-free approach to Bayesian inversion with an explicit representation of the parameter densities is developed. The approximation of the involved randomness inevitably leads to several high dimensional expressions, which are often tackled with classical sampling methods such as MCMC. To speed up these methods, the use of a surrogate model is beneficial since it allows for faster evaluation with respect to calibration parameters. However, the inherently slow convergence can not be remedied by this. As an alternative, a complete functional treatment of the inverse problem is feasible as demonstrated in this work, with functional representations of the parametric forward solution as well as the probability densities of the calibration parameters, determined by Bayesian inversion. The proposed sampling-free approach is discussed in the context of hierarchical tensor representations, which are employed for the adaptive evaluation of a random PDE (the forward problem) in generalized chaos polynomials and the subsequent high-dimensional quadrature of the log-likelihood. This modern compression technique alleviates the curse of dimensionality by hierarchical subspace approximations of the involved low rank (solution) manifolds. All required computations can be carried out efficiently in the low-rank format. A priori convergence is examined, considering all approximations that occur in the method. Numerical experiments demonstrate the performance and verify the theoretical results. -
M. Eigel, J. Neumann, R. Schneider, S. Wolf, Risk averse stochastic structural topology optimization, Computer Methods in Applied Mechanics and Engineering, 334 (2018), pp. 470--482, DOI 10.1016/j.cma.2018.02.003 .
Abstract
A novel approach for risk-averse structural topology optimization under uncertainties is presented which takes into account random material properties and random forces. For the distribution of material, a phase field approach is employed which allows for arbitrary topological changes during optimization. The state equation is assumed to be a high-dimensional PDE parametrized in a (finite) set of random variables. For the examined case, linearized elasticity with a parametric elasticity tensor is used. Instead of an optimization with respect to the expectation of the involved random fields, for practical purposes it is important to design structures which are also robust in case of events that are not the most frequent. As a common risk-aware measure, the Conditional Value at Risk (CVaR) is used in the cost functional during the minimization procedure. Since the treatment of such high-dimensional problems is a numerically challenging task, a representation in the modern hierarchical tensor train format is proposed. In order to obtain this highly efficient representation of the solution of the random state equation, a tensor completion algorithm is employed which only required the pointwise evaluation of solution realizations. The new method is illustrated with numerical examples and compared with a classical Monte Carlo sampling approach. -
L. Donati, M. Heida, M. Weber, B. Keller, Estimation of the infinitesimal generator by square-root approximation, Journal of Physics: Condensed Matter, 30 (2018), pp. 425201/1--425201/14, DOI 10.1088/1361-648X/aadfc8 .
Abstract
For the analysis of molecular processes, the estimation of time-scales, i.e., transition rates, is very important. Estimating the transition rates between molecular conformations is -- from a mathematical point of view -- an invariant subspace projection problem. A certain infinitesimal generator acting on function space is projected to a low-dimensional rate matrix. This projection can be performed in two steps. First, the infinitesimal generator is discretized, then the invariant subspace is approximated and used for the subspace projection. In our approach, the discretization will be based on a Voronoi tessellation of the conformational space. We will show that the discretized infinitesimal generator can simply be approximated by the geometric average of the Boltzmann weights of the Voronoi cells. Thus, there is a direct correlation between the potential energy surface of molecular structures and the transition rates of conformational changes. We present results for a 2d-diffusion process and Alanine dipeptide. -
M. Eigel, J. Neumann, R. Schneider, S. Wolf, Non-intrusive tensor reconstruction for high dimensional random PDEs, Computational Methods in Applied Mathematics, 19 (2019), pp. 39--53 (published online on 25.07.2018), DOI 10.1515/cmam-2018-0028 .
Abstract
This paper examines a completely non-intrusive, sample-based method for the computation of functional low-rank solutions of high dimensional parametric random PDEs which have become an area of intensive research in Uncertainty Quantification (UQ). In order to obtain a generalized polynomial chaos representation of the approximate stochastic solution, a novel black-box rank-adapted tensor reconstruction procedure is proposed. The performance of the described approach is illustrated with several numerical examples and compared to Monte Carlo sampling. -
F. Anker, Ch. Bayer, M. Eigel, M. Ladkau, J. Neumann, J.G.M. Schoenmakers, SDE based regression for random PDEs, SIAM Journal on Scientific Computing, 39 (2017), pp. A1168--A1200.
Abstract
A simulation based method for the numerical solution of PDE with random coefficients is presented. By the Feynman-Kac formula, the solution can be represented as conditional expectation of a functional of a corresponding stochastic differential equation driven by independent noise. A time discretization of the SDE for a set of points in the domain and a subsequent Monte Carlo regression lead to an approximation of the global solution of the random PDE. We provide an initial error and complexity analysis of the proposed method along with numerical examples illustrating its behaviour. -
F. Anker, Ch. Bayer, M. Eigel, J. Neumann, J.G.M. Schoenmakers, A fully adaptive interpolated stochastic sampling method for linear random PDEs, International Journal for Uncertainty Quantification, 7 (2017), pp. 189--205, DOI 10.1615/Int.J.UncertaintyQuantification.2017019428 .
Abstract
A numerical method for the fully adaptive sampling and interpolation of PDE with random data is presented. It is based on the idea that the solution of the PDE with stochastic data can be represented as conditional expectation of a functional of a corresponding stochastic differential equation (SDE). The physical domain is decomposed subject to a non-uniform grid and a classical Euler scheme is employed to approximately solve the SDE at grid vertices. Interpolation with a conforming finite element basis is employed to reconstruct a global solution of the problem. An a posteriori error estimator is introduced which provides a measure of the different error contributions. This facilitates the formulation of an adaptive algorithm to control the overall error by either reducing the stochastic error by locally evaluating more samples, or the approximation error by locally refining the underlying mesh. Numerical examples illustrate the performance of the presented novel method. -
M. Eigel, M. Pfeffer, R. Schneider, Adaptive stochastic Galerkin FEM with hierarchical tensor representations, Numerische Mathematik, 136 (2017), pp. 765--803.
Abstract
The solution of PDE with stochastic data commonly leads to very high-dimensional algebraic problems, e.g. when multiplicative noise is present. The Stochastic Galerkin FEM considered in this paper then suffers from the curse of dimensionality. This is directly related to the number of random variables required for an adequate representation of the random fields included in the PDE. With the presented new approach, we circumvent this major complexity obstacle by combining two highly efficient model reduction strategies, namely a modern low-rank tensor representation in the tensor train format of the problem and a refinement algorithm on the basis of a posteriori error estimates to adaptively adjust the different employed discretizations. The adaptive adjustment includes the refinement of the FE mesh based on a residual estimator, the problem-adapted stochastic discretization in anisotropic Legendre Wiener chaos and the successive increase of the tensor rank. Computable a posteriori error estimators are derived for all error terms emanating from the discretizations and the iterative solution with a preconditioned ALS scheme of the problem. Strikingly, it is possible to exploit the tensor structure of the problem to evaluate all error terms very efficiently. A set of benchmark problems illustrates the performance of the adaptive algorithm with higher-order FE. Moreover, the influence of the tensor rank on the approximation quality is investigated. -
F. Lanzara, V. Maz'ya, G. Schmidt, A fast solution method for time dependent multidimensional Schrödinger equations, Applicable Analysis. An International Journal, published online on 08.08.2017, urlhttps://doi.org/10.1080/00036811.2017.1359571, DOI 10.1080/00036811.2017.1359571 .
Abstract
In this paper we propose fast solution methods for the Cauchy problem for the multidimensional Schrödinger equation. Our approach is based on the approximation of the data by the basis functions introduced in the theory of approximate approximations. We obtain high order approximations also in higher dimensions up to a small saturation error, which is negligible in computations, and we prove error estimates in mixed Lebesgue spaces for the inhomogeneous equation. The proposed method is very efficient in high dimensions if the densities allow separated representations. We illustrate the efficiency of the procedure on different examples, up to approximation order 6 and space dimension 200. -
M.H. Farshbaf Shaker, R. Henrion, D. Hömberg, Properties of chance constraints in infinite dimensions with an application to PDE constrained optimization, Set-Valued and Variational Analysis. Theory and Applications. Springer, Dordrecht. English., 26 (2018), pp. 821--841 (published online on 11.10.2017), DOI 10.1007/s11228-017-0452-5 .
Abstract
Chance constraints represent a popular tool for finding decisions that enforce a robust satisfaction of random inequality systems in terms of probability. They are widely used in optimization problems subject to uncertain parameters as they arise in many engineering applications. Most structural results of chance constraints (e.g., closedness, convexity, Lipschitz continuity, differentiability etc.) have been formulated in a finite-dimensional setting. The aim of this paper is to generalize some of these well-known semi-continuity and convexity properties to a setting of control problems subject to (uniform) state chance constraints. -
M. Eigel, Ch. Merdon, J. Neumann, An adaptive multilevel Monte--Carlo method with stochastic bounds for quantities of interest in groundwater flow with uncertain data, SIAMASA J. Uncertain. Quantif., 4 (2016), pp. 1219--1245.
Abstract
The focus of this work is the introduction of some computable a posteriori error control to the popular multilevel Monte Carlo sampling for PDE with stochastic data. We are especially interested in applications in the geosciences such as groundwater flow with rather rough stochastic fields for the conductive permeability. With a spatial discretisation based on finite elements, a goal functional is defined which encodes the quantity of interest. The devised goal-oriented error estimator enables to determine guaranteed a posteriori error bounds for this quantity. In particular, it allows for the adaptive refinement of the mesh hierarchy used in the multilevel Monte Carlo simulation. In addition to controlling the deterministic error, we also suggest how to treat the stochastic error in probability. Numerical experiments illustrate the performance of the presented adaptive algorithm for a posteriori error control in multilevel Monte Carlo methods. These include a localised goal with problem-adapted meshes and a slit domain example. The latter demonstrates the refinement of regions with low solution regularity based on an inexpensive explicit error estimator in the multilevel algorithm. -
M. Eigel, Ch. Merdon, Local equilibration error estimators for guaranteed error control in adaptive stochastic higher-order Galerkin finite element methods, SIAM/ASA Journal on Uncertainty Quantification, 4 (2016), pp. 1372--1397.
Abstract
Equilibration error estimators have been shown to commonly lead to very accurate guaranteed error bounds in the a posteriori error control of finite element methods for second order elliptic equations. Here, we extend previous results by the design of equilibrated fluxes for higher-order finite element methods with nonconstant coefficients and illustrate the favourable performance of different variants of the error estimator within two deterministic benchmark settings. After the introduction of the respective parametric problem with stochastic coefficients and the stochastic Galerkin FEM discretisation, a novel a posteriori error estimator for the stochastic error in the energy norm is devised. The error estimation is based on the stochastic residual and its decomposition into approximation residuals and a truncation error of the stochastic discretisation. Importantly, by using the derived deterministic equilibration techniques for the approximation residuals, the computable error bound is guaranteed for the considered class of problems. An adaptive algorithm allows the simultaneous refinement of the deterministic mesh and the stochastic discretisation in anisotropic Legendre polynomial chaos. Several stochastic benchmark problems illustrate the efficiency of the adaptive process. -
F. Lanzara, V. Maz'ya, G. Schmidt, Approximation of solutions to multidimensional parabolic equations by approximate approximations, Applied and Computational Harmonic Analysis. Time-Frequency and Time-Scale Analysis, Wavelets, Numerical Algorithms, and Applications, 41 (2016), pp. 749--767.
-
M. Eigel, C.J. Gittelson, Ch. Schwab, E. Zander, A convergent adaptive stochastic Galerkin finite element method with quasi-optimal spatial meshes, ESAIM: Mathematical Modelling and Numerical Analysis, 49 (2015), pp. 1367--1398.
Abstract
We analyze a-posteriori error estimation and adaptive refinement algorithms for stochastic Galerkin Finite Element methods for countably-parametric elliptic boundary value problems. A residual error estimator which separates the effects of gpc-Galerkin discretization in parameter space and of the Finite Element discretization in physical space in energy norm is established. It is proved that the adaptive algorithm converges, and to this end we establish a contraction property satisfied by its iterates. It is shown that the sequences of triangulations which are produced by the algorithm in the FE discretization of the active gpc coefficients are asymptotically optimal. Numerical experiments illustrate the theoretical results. -
F. Lanzara, G. Schmidt, On the computation of high-dimensional potentials of advection-diffusion operators, Mathematika. A Journal of Pure and Applied Mathematics, 61 (2015), pp. 309--327.
-
W. Giese, M. Eigel, S. Westerheide, Ch. Engwer, E. Klipp, Influence of cell shape, inhomogeneities and diffusion barriers in cell polarization models, Physical Biology, 12 (2015), pp. 066014/1--066014/18.
Abstract
In silico experiments bear the potential to further the understanding of biological transport processes by allowing a systematic modification of any spatial property and providing immediate simulation results for the chosen models. We consider cell polarization and spatial reorganization of membrane proteins which are fundamental for cell division, chemotaxis and morphogenesis. Our computational study is motivated by mating and budding processes of S. cerevisiae. In these processes a key player during the initial phase of polarization is the GTPase Cdc42 which occurs in an active membrane-bound form and an inactive cytosolic form. We use partial differential equations to describe the membrane-cytosol shuttling of Cdc42 during budding as well as mating of yeast. The membrane is modeled as a thin layer that only allows lateral diffusion and the cytosol is modeled as a volume. We investigate how cell shape and diffusion barriers like septin structures or bud scars influence Cdc42 cluster formation and subsequent polarization of the yeast cell. Since the details of the binding kinetics of cytosolic proteins to the membrane are still controversial, we employ two conceptual models which assume different binding kinetics. An extensive set of in silico experiments with different modeling hypotheses illustrate the qualitative dependence of cell polarization on local membrane curvature, cell size and inhomogeneities on the membrane and in the cytosol. We examine that spatial inhomogenities essentially determine the location of Cdc42 cluster formation and spatial properties are crucial for the realistic description of the polarization process in cells. In particular, our computer simulations suggest that diffusion barriers are essential for the yeast cell to grow a protrusion. -
TH. Arnold, A. Rathsfeld, Reflection of plane waves by rough surfaces in the sense of Born approximation, Mathematical Methods in the Applied Sciences, 37 (2014), pp. 2091--2111.
Abstract
The topic of the present paper is the reflection of electromagnetic plane waves by rough surfaces, i.e., by smooth and bounded perturbations of planar faces. Moreover, the contrast between the cover material and the substrate beneath the rough surface is supposed to be low. In this case, a modification of Stearns' formula based on Born approximation and Fourier techniques is derived for a special class of surfaces. This class contains the graphs of functions if the interface function is a radially modulated almost periodic function. For the Born formula to converge, a sufficient and almost necessary condition is given. A further technical condition is defined, which guarantees the existence of the corresponding far field of the Born approximation. This far field contains plane waves, far-field terms like those for bounded scatterers, and, additionally, a new type of terms. The derived formulas can be used for the fast numerical computations of far fields and for the statistics of random rough surfaces. -
M. Eigel, C. Gittelson, Ch. Schwab, E. Zander, Adaptive stochastic Galerkin FEM, Computer Methods in Applied Mechanics and Engineering, 270 (2014), pp. 247--269.
-
F. Lanzara, V. Maz'ya, G. Schmidt, Fast cubature of volume potentials over rectangular domains by approximate approximations, Applied and Computational Harmonic Analysis. Time-Frequency and Time-Scale Analysis, Wavelets, Numerical Algorithms, and Applications, 36 (2014), pp. 167--182.
Abstract
In the present paper we study high-order cubature formulas for the computation of advection-diffusion potentials over boxes. By using the basis functions introduced in the theory of approximate approximations, the cubature of a potential is reduced to the quadrature of one dimensional integrals. For densities with separated approximation, we derive a tensor product representation of the integral operator which admits efficient cubature procedures in very high dimensions. Numerical tests show that these formulas are accurate and provide approximation of order O(h6) up to dimension 108.
 Contributions to Collected Editions
Contributions to Collected Editions
-
CH. Bayer, H. Oberhauser, Splitting methods for SPDEs: From robustness to financial engineering, optimal control and nonlinear filtering, in: Splitting Methods in Communication, Imaging, Science, and Engineering, R. Glowinski, S.J. Osher, W. Yin, eds., Scientific Computation, Springer International Publishing Switzerland, Cham, 2016, pp. 499--539.
Abstract
In this survey chapter we give an overview of recent applications of the splitting method to stochastic (partial) differential equations, that is, differential equations that evolve under the influence of noise. We discuss weak and strong approximations schemes. The applications range from the management of risk, financial engineering, optimal control and nonlinear filtering to the viscosity theory of nonlinear SPDEs.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
M. Eigel, Ch. Miranda, A. Nouy, D. Sommer, Approximation and learning with compositional tensor trains, Preprint no. 3253, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3253 .
Abstract, PDF (1203 kByte)
We introduce compositional tensor trains (CTTs) for the approximation of multivariate functions, a class of models obtained by composing low-rank functions in the tensor-train format. This format can encode standard approximation tools, such as (sparse) polynomials, deep neural networks (DNNs) with fixed width, or tensor networks with arbitrary permutation of the inputs, or more general affine coordinate transformations, with similar complexities. This format can be viewed as a DNN with width exponential in the input dimension and structured weights matrices. Compared to DNNs, this format enables controlled compression at the layer level using efficient tensor algebra. par On the optimization side, we derive a layerwise algorithm inspired by natural gradient descent, allowing to exploit efficient low-rank tensor algebra. This relies on low-rank estimations of Gram matrices, and tensor structured random sketching. Viewing the format as a discrete dynamical system, we also derive an optimization algorithm inspired by numerical methods in optimal control. Numerical experiments on regression tasks demonstrate the expressivity of the new format and the relevance of the proposed optimization algorithms. par Overall, CTTs combine the expressivity of compositional models with the algorithmic efficiency of tensor algebra, offering a scalable alternative to standard deep neural networks. -
M. Eigel, L. Grasedyck, Th. Le, J. Schütte, Neural and tensor networks for high-dimensional parametric PDEs and sampling, Preprint no. 3223, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3223 .
Abstract, PDF (16 MByte)
In this chapter, we present various methods based on neural network architectures and tensor decompositions for addressing parametric partial differential equations (PDEs) and sampling from unnormalized densities in high-dimensional settings. Parametric PDEs arise in many areas of science and engineering, where one seeks to solve a PDE efficiently for a wide range of parameter values or where the data is inherently uncertain. Such problems have been analysed extensively in Uncertainty Quantification in recent years. Directly related and also highly relevant for practical applications is a class of statistical inverse problems. It can be approached in a Bayesian framework through sampling techniques. par Two main strategies are central to this chapter: deconstructing complex problems into manageable, simpler subproblems in a sensible way and designing problem-specific model architectures that suit the specific properties and requirements of the problem at hand. The developed methods are supported by theoretical convergence guarantees and demonstrate state-of-the-art performance in numerical experiments. -
M. Eigel, C. Heiss, J. Schütte, Multi-level neural networks for high-dimensional parametric obstacle problems, Preprint no. 3193, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3193 .
Abstract, PDF (766 kByte)
A new method to solve computationally challenging (random) parametric obstacle problems is developed and analyzed, where the parameters can influence the related partial differential equation (PDE) and determine the position and surface structure of the obstacle. As governing equation, a stationary elliptic diffusion problem is assumed. The high-dimensional solution of the obstacle problem is approximated by a specifically constructed convolutional neural network (CNN). This novel algorithm is inspired by a finite element constrained multigrid algorithm to represent the parameter to solution map. This has two benefits: First, it allows for efficient practical computations since multi-level data is used as an explicit output of the NN thanks to an appropriate data preprocessing. This improves the efficacy of the training process and subsequently leads to small errors in the natural energy norm. Second, the comparison of the CNN to a multigrid algorithm provides means to carry out a complete a priori convergence and complexity analysis of the proposed NN architecture. Numerical experiments illustrate a state-of-the-art performance for this challenging problem. -
M. Eigel, Ch. Merdon, A posteriori error control for stochastic Galerkin FEM with high-dimensional random parametric PDEs, Preprint no. 3174, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3174 .
Abstract, PDF (5084 kByte)
PDEs with random data are investigated and simulated in the field of Uncertainty Quantification (UQ), where uncertainties or (planned) variations of coefficients, forces, domains and boundary con- ditions in differential equations formally depend on random events with respect to a pre-determined probability distribution. The discretization of these PDEs typically leads to high-dimensional (determin- istic) systems, where in addition to the physical space also the (often much larger) parameter space has to be considered. A proven technique for this task is the Stochastic Galerkin Finite Element Method (SGFEM), for which a review of the state of the art is provided. Moreover, important concepts and results are summarized. A special focus lies on the a posteriori error estimation and the derivation of an adaptive algorithm that controls all discretization parameters. In addition to an explicit residual based error estimator, also an equilibration estimator with guaranteed bounds is discussed. Under cer- tain mild assumptions it can be shown that the successive refinement produced by such an adaptive algorithm leads to a sequence of approximations with guaranteed convergence to the true solution. Nu- merical examples illustrate the practical behavior for some common benchmark problems. Additionally, an adaptive algorithm for a problem with a non-affine coefficient is shown. By transforming the original PDE a convection-diffusion problem is obtained, which can be treated similarly to the standard affine case. -
M. Eigel, J. Schütte, Multilevel CNNs for parametric PDEs based on adaptive finite elements, Preprint no. 3124, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3124 .
Abstract, PDF (2442 kByte)
A neural network architecture is presented that exploits the multilevel properties of high-dimensional parameter-dependent partial differential equations, enabling an efficient approximation of parameter-to-solution maps, rivaling best-in-class methods such as low-rank tensor regression in terms of accuracy and complexity. The neural network is trained with data on adaptively refined finite element meshes, thus reducing data complexity significantly. Error control is achieved by using a reliable finite element a posteriori error estimator, which is also provided as input to the neural network. par The proposed U-Net architecture with CNN layers mimics a classical finite element multigrid algorithm. It can be shown that the CNN efficiently approximates all operations required by the solver, including the evaluation of the residual-based error estimator. In the CNN, a culling mask set-up according to the local corrections due to refinement on each mesh level reduces the overall complexity, allowing the network optimization with localized fine-scale finite element data. par A complete convergence and complexity analysis is carried out for the adaptive multilevel scheme, which differs in several aspects from previous non-adaptive multilevel CNN. Moreover, numerical experiments with common benchmark problems from Uncertainty Quantification illustrate the practical performance of the architecture. -
M. Dambrine, C. Geiersbach, H. Harbrecht, Two-norm discrepancy and convergence of the stochastic gradient method with application to shape optimization, Preprint no. 3121, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3121 .
Abstract, PDF (447 kByte)
The present article is dedicated to proving convergence of the stochastic gradient method in case of random shape optimization problems. To that end, we consider Bernoulli's exterior free boundary problem with a random interior boundary. We recast this problem into a shape optimization problem by means of the minimization of the expected Dirichlet energy. By restricting ourselves to the class of convex, sufficiently smooth domains of bounded curvature, the shape optimization problem becomes strongly convex with respect to an appropriate norm. Since this norm is weaker than the differentiability norm, we are confronted with the so-called two-norm discrepancy, a well-known phenomenon from optimal control. We therefore need to adapt the convergence theory of the stochastic gradient method to this specific setting correspondingly. The theoretical findings are supported and validated by numerical experiments. -
D. Sommer, R. Gruhlke, M. Kirstein, M. Eigel, C. Schillings, Generative modelling with tensor train approximations of Hamilton--Jacobi--Bellman equations, Preprint no. 3078, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3078 .
Abstract, PDF (2117 kByte)
Sampling from probability densities is a common challenge in fields such as Uncertainty Quantification (UQ) and Generative Modelling (GM). In GM in particular, the use of reverse-time diffusion processes depending on the log-densities of Ornstein-Uhlenbeck forward processes are a popular sampling tool. In [5] the authors point out that these log-densities can be obtained by solution of a Hamilton-Jacobi-Bellman (HJB) equation known from stochastic optimal control. While this HJB equation is usually treated with indirect methods such as policy iteration and unsuper-vised training of black-box architectures like Neural Networks, we propose instead to solve the HJB equation by direct time integration, using compressed polynomials represented in the Tensor Train (TT) format for spatial discretization. Crucially, this method is sample-free, agnostic to normalization constants and can avoid the curse of dimensionality due to the TT compression. We provide a complete derivation of the HJB equation?s action on Tensor Train polynomials and demonstrate the performance of the proposed time-step-, rank- and degree-adaptive integration method on a nonlinear sampling task in 20 dimensions. -
M. Eigel, Ch. Miranda, J. Schütte, D. Sommer, Approximating Langevin Monte Carlo with ResNet-like neural network architectures, Preprint no. 3077, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3077 .
Abstract, PDF (795 kByte)
We sample from a given target distribution by constructing a neural network which maps samples from a simple reference, e.g. the standard normal distribution, to samples from the target. To that end, we propose using a neural network architecture inspired by the Langevin Monte Carlo (LMC) algorithm. Based on LMC perturbation results, we show approximation rates of the proposed architecture for smooth, log-concave target distributions measured in the Wasserstein-2 distance. The analysis heavily relies on the notion of sub-Gaussianity of the intermediate measures of the perturbed LMC process. In particular, we derive bounds on the growth of the intermediate variance proxies under different assumptions on the perturbations. Moreover, we propose an architecture similar to deep residual neural networks and derive expressivity results for approximating the sample to target distribution map. -
P. Trunschke, M. Eigel, A. Nouy, Weighted sparsity and sparse tensor networks for least squares approximation, Preprint no. 3049, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3049 .
Abstract, PDF (954 kByte)
The approximation of high-dimensional functions is a ubiquitous problem in many scientific fields that is only feasible practically if advantageous structural properties can be exploited. One prominent structure is sparsity relatively to some basis. For the analysis of these best n-term approximations a relevant tool is the Stechkin's lemma. In its standard form, however, this lemma does not allow to explain convergence rates for a wide range of relevant function classes. This work presents a new weighted version of Stechkin's lemma that improves the best n-term rates for weighted ℓp-spaces and associated function classes such as Sobolev or Besov spaces. For the class of holomorphic functions, which for example occur as solutions of common high-dimensional parameter dependent PDEs, we recover exponential rates that are not directly obtainable with Stechkin's lemma. This sparsity can be used to devise weighted sparse least squares approximation algorithms as known from compressed sensing. However, in high-dimensional settings, classical algorithms for sparse approximation suffer the curse of dimensionality. We demonstrate that sparse approximations can be encoded efficiently using tensor networks with sparse component tensors. This representation gives rise to a new alternating algorithm for best n-term approximation with a complexity scaling polynomially in n and the dimension. We also demonstrate that weighted ℓpsummability not only induces sparsity of the tensor but also low ranks. This is not exploited by the previous format. We thus propose a new low-rank tensor train format with a single weighted sparse core tensor and an ad-hoc algorithm for approximation in this format. To analyse the sample complexity for this new model class we derive a novel result of independent interest that allows to transfer the restricted isometry property from one set to another sufficiently close set. We then prove that the new model class is close enough to the set of weighted sparse vectors such that the restricted isometry property transfers. Numerical examples illustrate the theoretical results for a benchmark problem from uncertainty quantification. Although they lead up to the analysis of our final model class, our contributions on weighted Stechkin and the restricted isometry property are of independent interest and can be read independently. -
M. Heida, On the computation of high dimensional Voronoi diagrams, Preprint no. 3041, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3041 .
Abstract, PDF (553 kByte)
We investigate a recently implemented new algorithm for the computation of a Voronoi diagram in high dimensions and generalize it to N nodes in general or non-general position using a geometric characterization of edges merging in a given vertex. We provide a mathematical proof that the algorithm is exact, convergent and has computational costs of O(E*nn(N)), where E is the number of edges and nn(N) is the computational cost to calculate the nearest neighbor among N points. We also provide data from performance tests in the recently developed Julia package ,,HighVoronoi.jl”. -
M. Eigel, N. Hegemann, Guaranteed quasi-error reduction of adaptive Galerkin FEM for parametric PDEs with lognormal coefficients, Preprint no. 3036, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3036 .
Abstract, PDF (394 kByte)
Solving high-dimensional random parametric PDEs poses a challenging computational problem. It is well-known that numerical methods can greatly benefit from adaptive refinement algorithms, in particular when functional approximations in polynomials are computed as in stochastic Galerkin and stochastic collocations methods. This work investigates a residual based adaptive algorithm used to approximate the solution of the stationary diffusion equation with lognormal coefficients. It is known that the refinement procedure is reliable, but the theoretical convergence of the scheme for this class of unbounded coefficients remains a challenging open question. This paper advances the theoretical results by providing a quasi-error reduction results for the adaptive solution of the lognormal stationary diffusion problem. A computational example supports the theoretical statement. -
R. Gruhlke, M. Eigel, Low-rank Wasserstein polynomial chaos expansions in the framework of optimal transport, Preprint no. 2927, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2927 .
Abstract, PDF (10 MByte)
A unsupervised learning approach for the computation of an explicit functional representation of a random vector Y is presented, which only relies on a finite set of samples with unknown distribution. Motivated by recent advances with computational optimal transport for estimating Wasserstein distances, we develop a new Wasserstein multi-element polynomial chaos expansion (WPCE). It relies on the minimization of a regularized empirical Wasserstein metric known as debiased Sinkhorn divergence.As a requirement for an efficient polynomial basis expansion, a suitable (minimal) stochastic coordinate system X has to be determined with the aim to identify ideally independent random variables. This approach generalizes representations through diffeomorphic transport maps to the case of non-continuous and non-injective model classes M with different input and output dimension, yielding the relation Y=M(X) in distribution. Moreover, since the used PCE grows exponentially in the number of random coordinates of X, we introduce an appropriate low-rank format given as stacks of tensor trains, which alleviates the curse of dimensionality, leading to only linear dependence on the input dimension. By the choice of the model class M and the smooth loss function, higher order optimization schemes become possible. It is shown that the relaxation to a discontinuous model class is necessary to explain multimodal distributions. Moreover, the proposed framework is applied to a numerical upscaling task, considering a computationally challenging microscopic random non-periodic composite material. This leads to tractable effective macroscopic random field in adopted stochastic coordinates.
-
S. Riedel, Semi-implicit Taylor schemes for stiff rough differential equations, Preprint no. 2734, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2734 .
Abstract, PDF (538 kByte)
We study a class of semi-implicit Taylor-type numerical methods that are easy to implement and designed to solve multidimensional stochastic differential equations driven by a general rough noise, e.g. a fractional Brownian motion. In the multiplicative noise case, the equation is understood as a rough differential equation in the sense of T. Lyons. We focus on equations for which the drift coefficient may be unbounded and satisfies a one-sided Lipschitz condition only. We prove well-posedness of the methods, provide a full analysis, and deduce their convergence rate. Numerical experiments show that our schemes are particularly useful in the case of stiff rough stochastic differential equations driven by a fractional Brownian motion. -
M. Redmann, S. Riedel, Runge--Kutta methods for rough differential equations, Preprint no. 2708, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2708 .
Abstract, PDF (393 kByte)
We study Runge-Kutta methods for rough differential equations which can be used to calculate solutions to stochastic differential equations driven by processes that are rougher than a Brownian motion. We use a Taylor series representation (B-series) for both the numerical scheme and the solution of the rough differential equation in order to determine conditions that guarantee the desired order of the local error for the underlying Runge-Kutta method. Subsequently, we prove the order of the global error given the local rate. In addition, we simplify the numerical approximation by introducing a Runge-Kutta scheme that is based on the increments of the driver of the rough differential equation. This simplified method can be easily implemented and is computational cheap since it is derivative-free. We provide a full characterization of this implementable Runge-Kutta method meaning that we provide necessary and sufficient algebraic conditions for an optimal order of convergence in case that the driver, e.g., is a fractional Brownian motion with Hurst index 1/4 < H ≤ 1/2. We conclude this paper by conducting numerical experiments verifying the theoretical rate of convergence. -
M. Eigel, L. Grasedyck, R. Gruhlke, D. Moser, Low rank surrogates for polymorphic fields with application to fuzzy-stochastic partial differential equations, Preprint no. 2580, WIAS, Berlin, 2019, DOI 10.20347/WIAS.PREPRINT.2580 .
Abstract, PDF (1235 kByte)
We consider a general form of fuzzy-stochastic PDEs depending on the interaction of probabilistic and non-probabilistic ("possibilistic") influences. Such a combined modelling of aleatoric and epistemic uncertainties for instance can be applied beneficially in an engineering context for real-world applications, where probabilistic modelling and expert knowledge has to be accounted for. We examine existence and well-definedness of polymorphic PDEs in appropriate function spaces. The fuzzy-stochastic dependence is described in a high-dimensional parameter space, thus easily leading to an exponential complexity in practical computations. To aleviate this severe obstacle in practise, a compressed low-rank approximation of the problem formulation and the solution is derived. This is based on the Hierarchical Tucker format which is constructed with solution samples by a non-intrusive tensor reconstruction algorithm. The performance of the proposed model order reduction approach is demonstrated with two examples. One of these is the ubiquitous groundwater flow model with Karhunen-Loeve coefficient field which is generalized by a fuzzy correlation length.
 Talks, Poster
Talks, Poster
-
J. Schütte, Multilevel neural networks for high-dimensional parametric obstacle problems, The European Conference on Numerical Mathematics and Advanced Applications (ENUMATH) , Minisymposium ``MS55 Advancements and Applications of Solvers for PDE Systems with Nonsmooth Structures'', September 1 - 5, 2025, Universität Heidelberg, September 3, 2025.
-
M. Eigel, High-dimensional distribution sampling with applications in Bayesian inversion, Colloquium on Applied Mathematics, Universität Göttingen, Institut für Numerische Mathematik, February 4, 2025.
-
J. Schütte, Bayes for parametric PDEs with normalizing flows, SIAM Conference on Uncertainty Quantification (UQ24), Minisymposium MS37 ``Forward and Inverse Uncertainty Quantification for Nonlinear Problems'', February 27 - March 1, 2024, Savoia Excelsior Palace Trieste and Stazione Marittima, Italy, February 27, 2024.
-
M. Eigel, Adaptive multilevel neural networks for parametric PDEs with error control, 94th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2024), Session 15.05 ``Methodologies for Forward UQ'', March 18 - 22, 2024, Otto-von-Guericke-Universität Magdeburg, March 20, 2024.
-
M. Eigel, An operator network architecture for functional SDE representations, SIAM Conference on Uncertainty Quantification (UQ24), Minisymposium MS6 ``Operator Learning in Uncertainty Quantification'', February 27 - March 1, 2024, Savoia Excelsior Palace Trieste and Stazione Marittima, Italy, February 27, 2024.
-
M. Eigel, Sparse and compositional tensor formats for high-dimensional function approximation, Workshop ``High-dimensional Methods in Stochastic and Multiscale PDEs'', September 30 - October 2, 2024, Technische Universität Wien, Austria, October 2, 2024.
-
M. Eigel, Topology optimisation under uncertainties, modern tensor compression & empirical SFEM, UQ Colloquium, Bosch Research Campus, Renningen, October 11, 2024.
-
M. Heida, Voronoi diagrams and finite volume methods in any dimension, 94th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2024), Session 18.01 ``Discontinuous Galerkin and Software'', March 18 - 22, 2024, Otto-von-Guericke-Universität Magdeburg, March 19, 2024.
-
J. Schütte, Adaptive neural networks for parametric PDEs, Mini-Workshop ``Nonlinear Approximation of High-dimensional Functions in Scientific Computing, October 15 - 20, 2023, Mathematisches Forschungsinstitut Oberwolfach, October 20, 2023.
-
J. Schütte, Neural and tensor networks for parametric PDEs and inverse problems, Annual Meeting of SPP 2298, November 5 - 8, 2023, Evangelische Akademie, Tutzing, November 8, 2023.
-
M. Eigel, Accelerated interacting particle systems with low-rank tensor compression for Bayesian inversion, 5th International Conference on Uncertainty Quantification in Computational Science and Engineering (UNCECOMP 2023), MS9 ``UQ and Data Assimilation with Sparse, Low-rank Tensor, and Machine Learning Methods'', June 12 - 14, 2023, Athens, Greece, June 14, 2023.
-
M. Eigel, Accelerated interacting particle transport for Bayesian inversion, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Minisymposium 00966 ``Theoretical and Computational Advances in Measure Transport'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 21, 2023.
-
M. Eigel, Convergence of adaptive empirical stochastic Galerkin FEM, ECCOMAS Young Investigators Conference (YIC2023), Minisymposium CAM01 ``Uncertainty Quantification of Differential Equations with Random Parameters: Methods and Applications'', June 19 - 21, 2023, University of Porto, June 19, 2023.
-
M. Eigel, Convergence of an empirical Galerkin method for parametric PDEs, SIAM Conference on Computational Science and Engineering (CSE23), Minisymposium MS100 ``Randomized Solvers in Large-Scale Scientific Computing'', February 26 - March 3, 2023, Amsterdam, Netherlands, February 28, 2023.
-
M. Eigel, Functional SDE approximation inspired by a deep operator network architecture, Mini-Workshop ``Nonlinear Approximation of High-dimensional Functions in Scientific Computing'', October 15 - 20, 2023, Mathematisches Forschungsinstitut Oberwolfach, October 18, 2023.
-
J. Schütte, Adaptive neural networks for parametric PDE, 92th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2022), PP04: ``Theoretical Foundations of Deep Learning'', August 15 - 19, 2022, Rheinisch-Westfälische Technische Hochschule Aachen, August 16, 2022.
-
J. Schütte, Adaptive neural networks for parametric PDEs, Annual Meeting of SPP 2298, November 20 - 23, 2022, Evangelische Akademie, Tutzing, November 21, 2022.
-
J. Schütte, Adaptive neural tensor networks for parametric PDEs, Workshop on the Approximation of Solutions of High-Dimensional PDEs with Deep Neural Networks within the DFG Priority Programme 2298 ``Theoretical Foundations of Deep Learning'', May 30 - 31, 2022, Universität Bayreuth, May 31, 2022.
-
C. Geiersbach, Shape optimization under uncertainty: Challenges and algorithms, Helmut Schmidt Universität Hamburg, Mathematik im Bauingenieurwesen, April 26, 2022.
-
P.-É. Druet, Global existence and weak-strong uniqueness for isothermal ideal multicomponent flows, Against the Flow, October 18 - 22, 2022, Polish Academy of Sciences, Będlewo, Poland, October 19, 2022.
-
M. Eigel, Adaptive Galerkin FEM for non-affine linear parametric PDEs, Computational Methods in Applied Mathematics (CMAM 2022), MS06: ``Computational Stochastic PDEs'', August 29 - September 2, 2022, Technische Universität Wien, Austria, August 29, 2022.
-
M. Eigel, An empirical adaptive Galerkin method for parametric PDEs, Workshop ``Adaptivity, High Dimensionality and Randomness'' (Hybrid Event), April 4 - 8, 2022, Erwin Schrödinger International Institute for Mathematics and Physics, Vienna, Austria, April 6, 2022.
-
M. Eigel, Introduction to machine learning: Neural networks, Leibniz MMS Summer School 2021 ``Mathematical Methods for Machine Learning'', August 23 - 27, 2021, Schloss Dagstuhl, Leibniz-Zentrum für Informatik GmbH, Wadern, August 23, 2021.
-
S. Riedel, Runge--Kutta methods for rough differential equations (online talk), The DNA Seminar (spring 2020), Norwegian University of Science and Technology, Department of Mathematical Sciences, Trondheim, Norway, June 24, 2020.
-
S.-M. Stengl, Uncertainty quantification of the Ambrosio--Tortorelli approximation in image segmentation, Workshop on PDE Constrained Optimization under Uncertainty and Mean Field Games, January 28 - 30, 2020, WIAS, Berlin, January 30, 2020.
-
R. Gruhlke, Bayesian upscaling with application to failure analysis of adhesive bonds in rotor blades, 3rd International Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2019), Minisymposium 6--II ``Uncertainty Computations with Reduced Order Models and Low-Rank Representations'', June 24 - 26, 2019, Crete, Greece, June 24, 2019.
-
M. Eigel, A machine learning approach for explicit Bayesian inversion, Workshop 3 within the Special Semester on Optimization ``Optimization and Inversion under Uncertainty'', November 11 - 15, 2019, Johann Radon Institute for Computational and Applied Mathematics (RICAM), Linz, Austria, November 12, 2019.
-
M. Eigel, A statistical learning approach for high-dimensional PDEs, 3rd International Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2019), Minisymposium 6--IV ``Uncertainty Computations with Reduced Order Models and Low-Rank Representations'', June 24 - 26, 2019, Crete, Greece, June 25, 2019.
-
M. Eigel, A statistical learning approach for parametric PDEs, Workshop ``Scientific Computation using Machine-Learning Algorithms'', April 25 - 26, 2019, University of Nottingham, UK, April 26, 2019.
-
M. Eigel, A statistical learning approach for parametric PDEs, École Polytechnique Fédérale de Lausanne (EPFL), Scientific Computing and Uncertainty Quantification, Lausanne, Switzerland, May 14, 2019.
-
M. Eigel, Some thoughts on adaptive stochastic Galerkin FEM, Sixteenth Conference on the Mathematics of Finite Elements and Applications (MAFELAP 2019), Minisymposium 17 ``Finite Element Methods for Efficient Uncertainty Quantification'', June 18 - 21, 2019, Brunel University London, Uxbridge, UK, June 18, 2019.
-
M. Marschall, Adaptive low-rank approximation in Bayesian inverse problems, 3rd International Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2019), Minisymposium 6--IV ``Uncertainty Computations with Reduced Order Models and Low-Rank Representations'', June 24 - 26, 2019, Crete, Greece, June 25, 2019.
-
M. Marschall, Low-rank surrogates in Bayesian inverse problems, 19th French-German-Swiss Conference on Optimization (FGS'2019), Minisymposium 1 ``Recent Trends in Nonlinear Optimization 1'', September 17 - 20, 2019, Nice, France, September 17, 2019.
-
M. Marschall, Random domains in PDE problems with low-rank surrogates. Forward and backward, Physikalisch-Technische Bundesanstalt, Arbeitsgruppe 8.41 ``Mathematische Modellierung und Datenanalyse'', Berlin, April 10, 2019.
-
M. Eigel, Aspects of adaptive Galerkin FE for stochastic direct and inverse problems, Workshop ``Surrogate Models for UQ in Complex Systems'' (UNQW02), February 5 - 9, 2018, Isaac Newton Institute for Mathematical Sciences, Cambridge, UK, February 7, 2018.
-
S.-M. Stengl, Uncertainty quantification of the Ambrosio--Tortorelli approximation in image segmentation, MIA 2018 -- Mathematics and Image Analysis, Humboldt-Universität zu Berlin, January 15 - 17, 2018.
-
M. Eigel, R. Gruhlke, Domain decomposition for random high-dimensional PDEs, Workshop ``Reducing Dimensions and Cost for UQ in Complex Systems'', Cambridge, UK, March 5 - 9, 2018.
-
M. Eigel, Adaptive Galerkin FEM for stochastic forward and inverse problems, Optimisation and Numerical Analysis Seminars, University of Birmingham, School of Mathematics, UK, February 15, 2018.
-
M. Eigel, Adaptive tensor methods for forward and inverse problems, SIAM Conference on Uncertainty Quantification (UQ18), Minisymposium 122 ``Low-Rank Approximations for the Forward- and the Inverse Problems III'', April 16 - 19, 2018, Garden Grove, USA, April 19, 2018.
-
M. Marschall, Bayesian inversion with adaptive low-rank approximation, Analysis, Control and Inverse Problems for PDEs -- Workshop of the French-German-Italian LIA (Laboratoire International Associe) COPDESC on Applied Analysis, November 26 - 30, 2018, University of Naples Federico II and Accademia Pontaniana, Italy, November 29, 2018.
-
M. Eigel, A sampling-free adaptive Bayesian inversion with hierarchical tensor representations, European Conference on Numerical Mathematics and Advanced Applications (ENUMATH 2017), Minisymposium 15 ``Uncertainty Propagation'', September 25 - 29, 2017, Voss, Norway, September 27, 2017.
-
M. Eigel, Adaptive stochastic FE for explicit Bayesian inversion with hierarchical tensor representations, Institut National de Recherche en Informatique et en Automatique (INRIA), SERENA (Simulation for the Environment: Reliable and Efficient Numerical Algorithms) research team, Paris, France, June 1, 2017.
-
M. Eigel, Adaptive stochastic Galerkin FE and tensor compression for random PDEs, sc Matheon Workshop ``Reliable Methods of Mathematical Modeling'' (RMMM8), July 31 - August 4, 2017, Humboldt-Universität zu Berlin, August 3, 2017.
-
M. Eigel, Aspects of stochastic Galerkin FEM, Universität Basel, Mathematisches Institut, Switzerland, November 10, 2017.
-
M. Eigel, Efficient Bayesian inversion with hierarchical tensor representation, 2nd International Conference on Uncertainty Quantification in Computational Sciences and Engineering (UNCECOMP 2017), June 15 - 17, 2017, Rhodos, Greece, June 16, 2017.
-
M. Eigel, Explicit Bayesian inversion in hierarchical tensor representations, 4th GAMM Junior's and 1st GRK2075 Summer School 2017 ``Bayesian Inference: Probabilistic Way of Learning from Data'', July 10 - 14, 2017, Braunschweig, July 14, 2017.
-
M. Eigel, Stochastic topology optimization with hierarchical tensor reconstruction, Frontiers of Uncertainty Quantification in Engineering (FrontUQ 2017), September 6 - 8, 2017, München, September 7, 2017.
-
R. Gruhlke, Multi-scale failure analysis with polymorphic uncertainties for optimal design of rotor blades, Frontiers of Uncertainty Quantification in Engineering (FrontUQ 2017), September 6 - 8, 2017, München, September 6, 2017.
-
M. Marschall, Bayesian inversion using hierarchical tensors, 88th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2017), Section S15 ``Uncertainty Quantification'', March 6 - 10, 2017, Bauhaus Universität Weimar/Technische Universität Ilmenau, Weimar, March 8, 2017.
-
M. Marschall, Sampling-free Bayesian inversion with adaptive hierarchical tensor representation, Frontiers of Uncertainty Quantification in Engineering (FrontUQ 2017), September 6 - 8, 2017, München, September 7, 2017.
-
M. Marschall, Sampling-free Bayesian inversion with adaptive hierarchical tensor representation, International Conference on Scientific Computation and Differential Equations (SciCADE2017), MS21 ``Tensor Approximations of Multi-Dimensional PDEs'', September 11 - 15, 2017, University of Bath, UK, September 14, 2017.
-
M. Eigel, Adaptive stochastic Galerkin FEM with hierarchical tensor representations, Advances in Uncertainty Quantification Methods, Algorithms and Applications (UQAW 2016), January 5 - 10, 2016, King Abdullah University of Science and Technology (KAUST), Thuwal, Saudi Arabia, January 8, 2016.
-
M. Eigel, Adaptive stochastic Galerkin FEM with hierarchical tensor representations, 15th Conference on the Mathematics of Finite Elements and Applications (Brunel MAFELAP 2016), Minisymposium ``Uncertainty Quantification Using Stochastic PDEs and Finite Elements'', June 14 - 17, 2016, Brunel University London, Uxbridge, UK, June 14, 2016.
-
M. Eigel, Adaptive stochastic Galerkin FEM with hierarchical tensor representations, Joint Annual Meeting of DMV and GAMM, Section 18 ``Numerical Methods of Differential Equations'', March 7 - 11, 2016, Technische Universität Braunschweig, March 10, 2016.
-
M. Eigel, Bayesian inversion using hierarchical tensor approximations, SIAM Conference on Uncertainty Quantification, Minisymposium 67 ``Bayesian Inversion and Low-rank Approximation (Part II)'', April 5 - 8, 2016, Lausanne, Switzerland, April 6, 2016.
-
M. Eigel, Some aspects of adaptive random PDEs, Oberseminar, Rheinisch-Westfälische Technische Hochschule Aachen, Institut für Geometrie und Praktische Mathematik, July 21, 2016.
-
J. Neumann, Adaptive SDE based sampling for random PDE, SIAM Conference on Uncertainty Quantification, Minisymposium 142 ``Error Estimation and Adaptive Methods for Uncertainty Quantification in Computational Sciences -- Part II'', April 5 - 8, 2016, Lausanne, Switzerland, April 8, 2016.
-
J. Neumann, The phase field approach for topology optimization under uncertainties, ZIB Computational Medicine and Numerical Mathematics Seminar, Konrad-Zuse-Zentrum für Informationstechnik Berlin, August 25, 2016.
-
J. Pellerin, RINGMesh: A programming library for geological model meshes, The 17th annual conference of the International Association for Mathematical Geosciences, September 5 - 13, 2015, Freiberg, September 8, 2015.
-
M. Eigel, Adaptive stochastic Galerkin FEM with hierarchical tensor representations, 2nd GAMM AGUQ Workshop on Uncertainty Quantification, September 10 - 11, 2015, Chemnitz, September 10, 2015.
-
M. Eigel, Fully adaptive higher-order stochastic Galerkin FEM in low-rank tensor representation, International Conference on Scientific Computation And Differential Equations (SciCADE 2015), September 14 - 18, 2015, Universität Potsdam, September 15, 2015.
-
M. Eigel, Guaranteed error bounds for adaptive stochastic Galerkin FEM, Technische Universität Braunschweig, Institut für Wissenschaftliches Rechnen, April 1, 2015.
-
M. Eigel, Stochastic adaptive FEM, Forschungsseminar Numerische Mathematik, Humboldt-Universität zu Berlin, Institut für Mathematik, January 28, 2015.
-
CH. Bayer, SDE based regression for random PDEs, Direct and Inverse Problems for PDEs with Random Coefficients, WIAS Berlin, November 13, 2015.
-
M. Eigel, A posteriori error control in stochastic FEM and MLMC, 27th Chemnitz FEM Symposium 2014, September 22 - 24, 2014, September 24, 2014.
-
M. Eigel, Adaptive spectral methods for stochastic optimisation problems, Technische Universität Berlin, Institut für Mathematik, May 22, 2014.
-
M. Eigel, Adaptive stochastic FEM, Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen (IWR), June 5, 2014.
-
M. Eigel, Guaranteed a posteriori error control with adaptive stochastic Galerkin FEM, SIAM Conference on Uncertainty Quantification (UQ14), March 31 - April 3, 2014, Savannah, USA, April 1, 2014.
-
M. Ladkau, Brownian motion approach for spatial PDEs with stochastic data, International Workshop ``Advances in Optimization and Statistics'', May 15 - 16, 2014, Russian Academy of Sciences, Institute of Information Transmission Problems (Kharkevich Institute), Moscow, May 16, 2014.
-
J. Neumann, A posteriori error estimators for problems with uncertain data, Norddeutsches Kolloquium über Angewandte Analysis und Numerische Mathematik (NoKo), Christian-Albrechts-Universität zu Kiel, May 10, 2014.
-
J. Neumann, Stochastic bounds for quantities of interest in groundwater flow with uncertain data, Université Paris-Sud, Laboratoire d'Analyse Numérique, Orsay, France, October 9, 2014.
 External Preprints
External Preprints
-
M. Eigel, J. Schütte, Adaptive multilevel neural networks for parametric PDEs with error estimation, Preprint no. arXiv:2403.12650, Cornell University, 2024, DOI 10.48550/arXiv.2403.12650 .
-
P. Trunschke, A. Nouy, M. Eigel, Weighted sparsity and sparse tensor networks for least squares approximation, Preprint no. arXiv:2310.08942, Cornell University, 2023, DOI 10.48550/arXiv.2310.08942 .


