Modern semiconductor devices and optoelectronic devices such as semiconductor lasers or solar cells are based on semiconductor structures, which e.g. can be given by doping profiles, hetero- or nanostructures. For the qualitative and quantitative understanding of the properties of these devices, mathematical modeling and simulation of the most relevant and, respectively, of the limiting carrier transport processes is necessary.
Current research also focuses on the improvement of energy efficiency of new devices and the development of novel technologies for applications in renewable energies, communication, and lighting. This topic, which is also called Green Photonics, is one of the essential technological challenges for the coming years. The Weierstrass Institute actively contributes to the fundamental and application-driven research and development of novel solutions.
Drift-diffusion models are well established for the description of carrier transport in semiconductor devices. The van Roosbroeck system is the basic model. It describes the motion of negatively and positively charged carriers (electrons and holes) in a self-consistent electrical field by drift and diffusion.
On the one hand, the research in this application area is focused on the development and investigation of mathematical modeling approaches for taking into account additional important physical effects. On the other hand, the emphasis is on the development of fast and robust numerical methods for the solution of the coupled model equations. The particular research goals often arise from challenging problems of collaborators.
The Weierstrass Institute has a long tradition in mathematical modeling and numerical simulation of semiconductor materials. Many analytical results for the systems of partial differential equations that describe the behavior of complex semiconductor structures have been published in the past and also several software packages have been developed: WIAS-TeSCA, WIAS-QW, ddfermi.
However, new technologies are changing fast and they require new methodologies. At WIAS different aspects are nowadays under consideration:
- New tools for the mathematical analysis such as gradient structures
- Further analytical results for coupled models like for example transport equations coupled with quantum mechanical system
- New mathematical models for innovative materials: organic semiconductors (see Matheon project SE2, ECMath project SE18, MATH+ project AA2-1)
- Study of different numerical schemes which can deal with specific physical situations for example cryogenic temperature
- Development of a new simulation software: ddfermi
- Doping and topology optimization (see Matheon project OT1)
Highlights
Organic semiconductor devices
In close cooperation with our partners from the Dresden Integrated Center for Applied Physics and Photonic Materials (IAPP, TU Dresden) we model and simulate organic semiconductor devices such as organic transistors (OPBTs, VOFETs) as well as organic light-emitting diodes (OLEDs). One crucial feature of organic devices is the temperature-activated hopping transport of charge carriers. In connection with Joule self-heating this leads to a complex interplay that eventually results in S-shaped current-voltage characteristics and can lead to brightness inhomogeneities in large-area OLEDs.
Together with the IAPP we derived an empirical PDE thermistor model. It is based on a p(x)-Laplace operator that takes the non-Ohmic behavior of the organic layers into account and an Arrhenius law whose activation energy describes the energetic disorder in organic materials. The model was implemented in a simulation tool capable of simulating the electrothermal interplay in large-area OLEDs including S-shaped characteristics with regions of negative differential resistance.
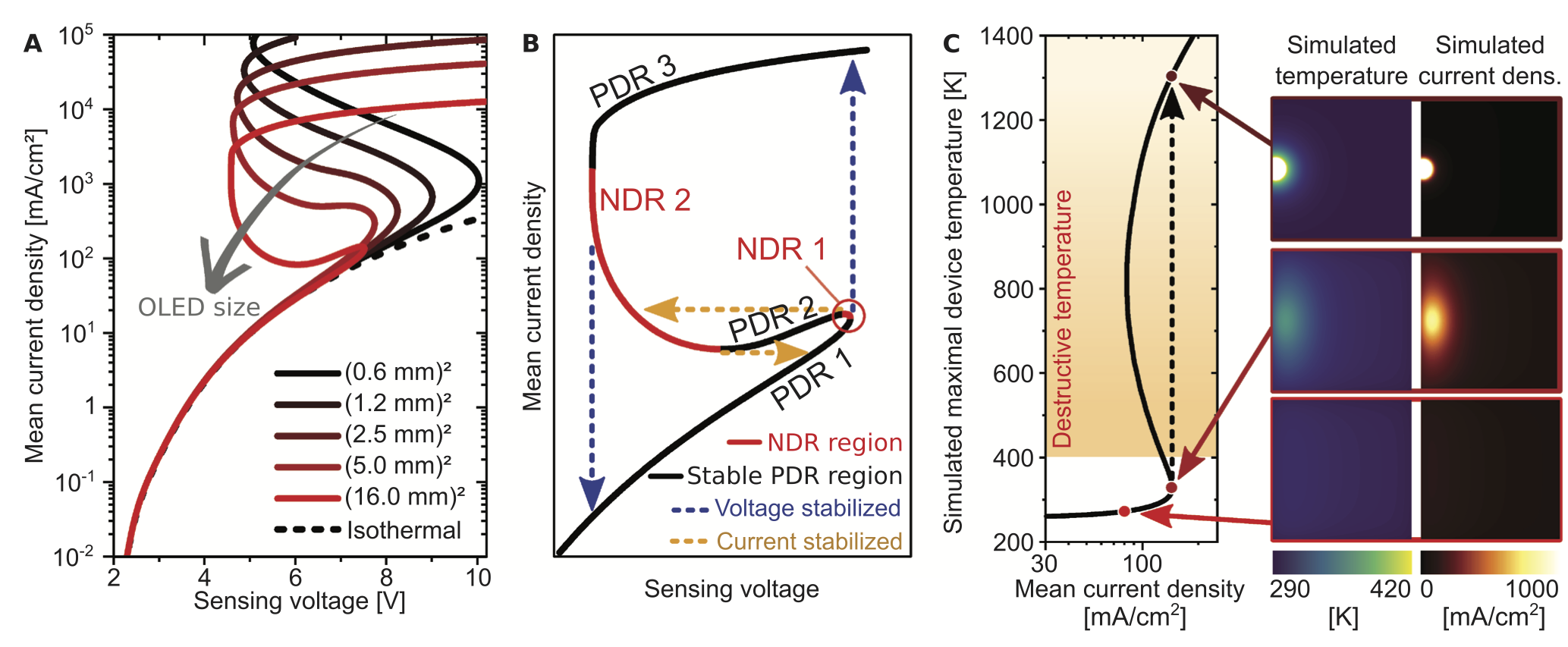 With IAPP an undiscovered tristability in large-area OLEDs was found. It provokes switching processes and sudden burn-in phenomena in LEDs that cannot be prevented by current- nor by voltage-controlled operation mode. Simulations of devices with sufficiently large ratio of area to thickness of the device show even three stable operating branches for certain ranges of voltage.
With IAPP an undiscovered tristability in large-area OLEDs was found. It provokes switching processes and sudden burn-in phenomena in LEDs that cannot be prevented by current- nor by voltage-controlled operation mode. Simulations of devices with sufficiently large ratio of area to thickness of the device show even three stable operating branches for certain ranges of voltage. Mathematical optimization of optoelectronic device designs
Silicon photonics has become a rapidly developing new field with a high potential for low-cost solutions to problems ranging from high-speed data transfer for optical on-chip communication to bio-sensing. However, for optoelectronic applications, the missing piece in silicon photonics is a monolithically integrated light source. For this, a promising candidate is germanium, since its optical properties can be influenced and enhanced by applying a mechanical strain and electronical doping.
To understand their potential in performance, in close collaboration with IHP (Innovations for High Performance microelectronics, Frankfurt Oder), we model, simulate, and optimize the design of germanium-on-silicon microstrips to enable sufficient light emission. To determine the influence of the macroscopic mechanical strain and the doping on the optoelectronic properties of the device, we developed a multiscale model, see IEEE Photonics (DOI:10.1109/JPHOT.2015.2427093).
Using this model, we carried out exemplary robustness studies, see OQE (DOI:10.1007/s11082-016-0394-4). The model is also the basis for the development of mathematical tools for a systematic topology and doping optimization based on second order methods for the underlying PDE systems, e.g. see Journal of Computational and Theoretical Transport (DOI:10.1080/23324309.2016.1189940). An overview to this approach is also given in the WIAS Annual Research Report 2015.
Publications
 Monographs
Monographs
-
U.W. Pohl, A. Strittmatter, A. Schliwa, M. Lehmann, T. Niermann, T. Heindel, S. Reitzenstein, M. Kantner, U. Bandelow, Th. Koprucki, H.-J. Wünsche, Chapter 3: Stressor-Induced Site Control of Quantum Dots for Single-Photon Sources, in Semiconductor Nanophotonics, M. Kneissl, A. Knorr, S. Reitzenstein, A. Hoffmann, eds., 194 of Springer Series in Solid-State Sciences, Springer, Heidelberg, 2020, pp. 53--90, (Chapter Published), DOI 10.1007/978-3-030-35656-9_3 .
Abstract
The strain field of selectively oxidized A10x current apertures in an A1GaAs/GaAs mesa is utilized to define the nucleation site of InGaAs/GaAs quantum dots. A design is developed that allows for the self-aligned growth of single quantum dots in the center of a circular mesa. Measurements of the strain tensor applying transmission-electron holography yield excellent agreement with the calculated strain field. Single-dot spectroscopy of site-controlled dots proves narrow excitonic linewidth virtually free of spectral diffusion due to quantum-dot growth in a defect-free matrix. Implementation of such dots in an electrically driven pin structure yields single-dot electroluminescence. Single-photon emission with excellent purity is provided for this device using a Hanbury Brown and Twiss setup. The injection efficiency of the initian pin design is affected by a substantial lateral current spreading close to the oxide aperture. Allpying 3D carier-transport simulation a ppn doping profile is developed achieving a substantial improvement of the current injection. -
S. Rodt, P.-I. Schneider, L. Zschiedrich, T. Heindel, S. Bounouar, M. Kantner, Th. Koprucki, U. Bandelow, S. Burger, S. Reitzenstein, Chapter 8: Deterministic Quantum Devices for Optical Quantum Communication, in: Semiconductor Nanophotonics, M. Kneissl, A. Knorr, S. Reitzenstein, A. Hoffmann, eds., 194 of Springer Series in Solid-State Sciences, Springer, Heidelberg, 2020, pp. 285--359, (Chapter Published), DOI 10.1007/978-3-030-35656-9_8 .
Abstract
Photonic quantum technologies are based on the exchange of information via single photons. The information is typically encoded in the polarization of the photons and security is ensured intrinsically via principles of quantum mechanics such as the no-cloning theorem. Thus, all optical quantum communication networks rely crucially on the availability of suitable quantum-light sources. Such light sources with close to ideal optical and quantum optical properties can be realized by self-assembled semiconductor quantum dots. These high-quality nanocrystals are predestined single-photon emitters due to their quasi zero-dimensional carrier confinement. Still, the development of practical quantum-dot-based sources of single photons and entangled-photon pairs for applications in photonic quantum technology and especially for the quantum-repeater scheme is very demanding and requires highly advanced device concepts and deterministic fabrication technologies. This is mainly explained by their random position and emission energy as well as by the low photon-extraction efficiency in simple planar device configurations. -
M. Kantner, Th. Höhne, Th. Koprucki, S. Burger, H.-J. Wünsche, F. Schmidt, A. Mielke, U. Bandelow, Chapter 7: Multi-Dimensional Modeling and Simulation of Semiconductor Nanophotonic Devices, in: Semiconductor Nanophotonics, M. Kneissl, A. Knorr, S. Reitzenstein, A. Hoffmann, eds., 194 of Springer Series in Solid-State Sciences, Springer, Heidelberg, 2020, pp. 241--283, (Chapter Published), DOI 10.1007/978-3-030-35656-9_7 .
Abstract
Self-consistent modeling and multi-dimensional simulation of semiconductor nanophotonicdevices is an important tool in the development of future integrated light sources and quantumdevices. Simulations can guide important technological decisions by revealing performance bottle-necks in new device concepts, contribute to their understanding and help to theoretically exploretheir optimization potential. The efficient implementation of multi-dimensional numerical simulationsfor computer-aided design tasks requires sophisticated numerical methods and modeling tech-niques. We review recent advances in device-scale modeling of quantum dot based single-photonsources and laser diodes by self-consistently coupling the optical Maxwell equations with semi-classical carrier transport models using semi-classical and fully quantum mechanical descriptionsof the optically active region, respectively. For the simulation of realistic devices with complex,multi-dimensional geometries, we have developed a novel hp-adaptive finite element approachfor the optical Maxwell equations, using mixed meshes adapted to the multi-scale properties ofthe photonic structures. For electrically driven devices, we introduced novel discretization andparameter-embedding techniques to solve the drift-diffusion system for strongly degenerate semi-conductors at cryogenic temperature. Our methodical advances are demonstrated on variousapplications, including vertical-cavity surface-emitting lasers, grating couplers and single-photonsources. -
M. Kantner, Electrically Driven Quantum Dot Based Single-Photon Sources: Modeling and Simulation, Springer Theses, Springer, Cham, 2020, XVII, 180 pages, (Monograph Published), DOI 10.1007/978-3-030-39543-8 .
Abstract
Semiconductor quantum optics is on the verge of moving from the lab to real world applications. When stepping from basic research to new technologies, device engineers will need new simulation tools for the design and optimization of quantum light sources, which combine classical device physics with cavity quantum electrodynamics. This thesis aims to provide a holistic description of single-photon emitting diodes by bridging the gap between microscopic and macroscopic modeling approaches. The central result is a novel hybrid quantum-classical model system that self-consistently couples semi-classical carrier transport theory with open quantum many-body systems. This allows for a comprehensive description of quantum light emitting diodes on multiple scales: It enables the calculation of the quantum optical figures of merit together with the simulation of the spatially resolved current flow in complex, multi-dimensional semiconductor device geometries out of one box. The hybrid system is shown to be consistent with fundamental laws of (non-)equilibrium thermodynamics and is demonstrated by numerical simulations of realistic devices. -
P. Farrell, N. Rotundo, D.H. Doan, M. Kantner, J. Fuhrmann, Th. Koprucki, Chapter 50: Drift-Diffusion Models, in: Vol. 2 of Handbook of Optoelectronic Device Modeling and Simulation: Lasers, Modulators, Photodetectors, Solar Cells, and Numerical Methods, J. Piprek, ed., Series in Optics and Optoelectronics, CRC Press, Taylor & Francis Group, Boca Raton, 2017, pp. 733--771, (Chapter Published).
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
-
A. Zisowsky, A. Arnold, M. Ehrhardt, Th. Koprucki, Chapter 7: Transient Simulation of k$cdot$p-Schrödinger Systems Using Discrete Transparent Boundary Conditions, in: Multi-Band Effective Mass Approximations -- Advanced Mathematical Models and Numerical Techniques, M. Ehrhardt, Th. Koprucki, eds., 94 of Lecture Notes in Computational Science and Engineering, Springer, Cham et al., 2014, pp. 247--272, (Chapter Published).
-
D. Klindworth, M. Ehrhardt, Th. Koprucki, Chapter 8: Discrete Transparent Boundary Conditions for Multi-band Effective Mass Approximations, in: Multi-Band Effective Mass Approximations -- Advanced Mathematical Models and Numerical Techniques, M. Ehrhardt, Th. Koprucki, eds., 94 of Lecture Notes in Computational Science and Engineering, Springer, Cham et al., 2014, pp. 273--318, (Chapter Published).
-
M. Ehrhardt, Th. Koprucki, eds., Multi-Band Effective Mass Approximations --- Advanced Mathematical Models and Numerical Techniques, 94 of Lecture Notes in Computational Science and Engineering, Springer, Cham et al., 2014, xvi+318 pages, (Monograph Published).
-
U. Bandelow, H. Gajewski, R. Hünlich, Chapter 3: Fabry--Perot Lasers: Thermodynamics-based Modeling, in: Optoelectronic Devices --- Advanced Simulation and Analysis, J. Piprek, ed., Springer, New York, 2005, pp. 63-85, (Chapter Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
D. Abdel, J. Relle, Th. Kirchartz, P. Jaap, J. Fuhrmann, S. Burger, Ch. Becker, K. Jäger, P. Farrell, How nanotextured interfaces influence the electronics in perovskite solar cells, The R Journal, (2026), pp. D5EL00208G/1--D5EL00208G/12, DOI 10.1039/D5EL00208G .
Abstract
Perovskite solar cells have reached power conversion efficiencies that rival those of established silicon photovoltaic technologies. Nanotextures in perovskite solar cells optimise light trapping and scattering, thereby improving optical absorption. In addition, nanotextures have been experimentally shown to enhance electronic performance, in particular, by increasing the open- circuit voltage VOC - a phenomenon that, until now, has remained not fully understood. This study investigates the underlying reasons by combining multi-dimensional optical and charge- transport simulations for a single-junction perovskite solar cell. Our results reveal that the increased open-circuit voltage is not driven by optical effects but by the textured geometry itself. For voltages near VOC, texturing one of the absorber/transport layer interfaces increases the imbalance between electron and hole densities in the absorber, thereby reducing Shockley-Read- Hall (SRH) recombination, which is the dominant loss mechanism in this study. While idealised solar cells benefit unconditionally from increasing texture height, in realistic cells there is an optimal texture height which maximizes the power conversion efficiency. These findings provide new insights into the opto-electronic advantages of texturing and offer guidance for the design of next-generation textured perovskite-based solar cells, light emitting diodes, and photodetectors. -
D. Abdel, M. Herda, M. Ziegler, C. Chainais-Hillairet, B. Spetzler, P. Farrell, Numerical analysis and simulation of lateral memristive devices: Schottky, ohmic, and multi-dimensional electrode models, Computers & Mathematics with Applications. An International Journal, 199 (2025), pp. 286--308, DOI 10.1016/j.camwa.2025.09.034 .
Abstract
In this paper, we present the numerical analysis and simulations of a multi-dimensional memristive device model. Memristive devices and memtransistors based on two-dimensional (2D) materials have demonstrated promising potential as components for next-generation artificial intelligence (AI) hardware and information technology. Our charge transport model describes the drift-diffusion of electrons, holes, and ionic defects self-consistently in an electric field. We incorporate two types of boundary models: ohmic and Schottky contacts. The coupled drift-diffusion partial differential equations are discretized using a physics-preserving Voronoi finite volume method. It relies on an implicit time-stepping scheme and the excess chemical potential flux approximation. We demonstrate that the fully discrete nonlinear scheme is unconditionally stable, preserving the free-energy structure of the continuous system and ensuring the non-negativity of carrier densities. Novel discrete entropy-dissipation inequalities for both boundary condition types in multiple dimensions allow us to prove the existence of discrete solutions. We perform multi-dimensional simulations to understand the impact of electrode configurations and device geometries, focusing on the hysteresis behavior in lateral 2D memristive devices. Three electrode configurations - side, top, and mixed contacts - are compared numerically for different geometries and boundary conditions. These simulations reveal the conditions under which a simplified one-dimensional electrode geometry can well represent the three electrode configurations. This work lays the foundations for developing accurate, efficient simulation tools for 2D memristive devices and memtransistors, offering tools and guidelines for their design and optimization in future applications. -
M. O'Donovan, R. Finn, P. Farrell, T. Streckenbach, J. Moatti, S. Schulz, Th. Koprucki, Developing a hybrid single band carrier transport model for (Al,Ga)N heterostructures, Journal of Computational Electronics, 24 (2025), pp. 114/1--114/19 (published online on 13.06.2025), DOI 10.1007/s10825-025-02333-2 .
Abstract
Aluminium gallium nitride (Al,Ga)N alloys and heterostructures are used in the development of UV light emitting devices, and can emit at energies extending into the UV-C spectral range. In the UV-C wavelength window and thus at high AlN content, devices exhibit poor quantum efciencies. In order to aid the development of these devices, simulation techniques which capture the essential physics of these materials and heterostructures should be used. Due to a change in band ordering in a quantum well at compositions close to Al0.75Ga0.25N, special attention should be given to the treatment of valence band states in device simulation. In this work we develop a hybrid single band efective mass model which is informed by degree of optical polarization data obtained from atomistic multi-band calculations. Overall, the hybrid single band efective mass model is benchmarked against tight-binding electronic structure calculations. To do so a confining energy landscape is extracted from the tight-binding model and used as input for the single band efective mass calculations. Moreover, the extracted tight-binding energy landscape is transferred to a drift-difusion model, allowing therefore for a multi-scale study of transport properties of a single (Al,Ga)N quantum well embedded in a p-i-n junction. Our results show that wider wells lead to a lower turn-on voltage due to a reduction of the band gap, but the internal quantum efciency of these wells is lower than in narrower wells. Alloy disorder leads to carrier localization and an uneven distribution of recombination within the quantum well plane, which gives rise to percolation currents. A comparison of results with 'pure' band simulations shows that when TE emission dominated, the heavy hole mass is a good approximation. In contrast, where band mixing was strong between heavy hole and split-of bands the mass from the split of band was very efective. -
C.L. Manganelli, D. Spirito, P. Farrell, J. Frigerio, A. De Lacovo, D. Marian, M. Virgilio, Strain engineering in semiconductor materials, physica status solidi (RLL) -- Rapid Research Letters (pss RRL), 19 (2025), pp. 2400383/1--2400383/3, DOI 10.1002/pssr.202400383 .
Abstract
Strain engineering has become an essential strategy in the advancement of semiconductor technologies, providing a power- ful mean to modulate the electronic, optical, and mechanical properties of materials. By introducing controlled deformation into crystal lattices, this approach enables enhanced carrier mobility, tailored bandgap energies, and improved device perfor- mance across applications in photonics, optoelectronics, and quantum technologies. -
G. Alì, P. Farrell, N. Rotundo, Forward lateral photovoltage scanning problem: Perturbation approach and existence-uniqueness analysis, Journal of Mathematical Analysis and Applications, 541 (2025), pp. 128725/1--128725/22, DOI 10.1016/j.jmaa.2024.128725 .
Abstract
In this paper, we present analytical results for the so-called forward lateral photovoltage scanning (LPS) problem. The (inverse) LPS model predicts doping variations in crystal by measuring the current leaving the crystal generated by a laser at various positions. The forward model consists of a set of nonlinear elliptic equations coupled with a measuring device modeled by a resistance. Standard methods to ensure the existence and uniqueness of the forward model cannot be used in a straightforward manner due to the presence of an additional generation term modeling the effect of the laser on the crystal. Hence, we scale the original forward LPS problem and employ a perturbation approach to derive the leading order system and the correction up to the second order in an appropriate small parameter. While these simplifications pose no issues from a physical standpoint, they enable us to demonstrate the analytic existence and uniqueness of solutions for the simplified system using standard arguments from elliptic theory adapted to the coupling with the measuring device. -
A. Glitzky, M. Liero, Uniqueness and regularity of weak solutions of a drift-diffusion system for perovskite solar cells, Journal of Evolution Equations, 25 (2025), pp. 87/1--87/23, DOI 10.1007/s00028-025-01117-2 .
Abstract
We establish a novel uniqueness result for an instationary drift-diffusion model for perovskite solar cells. This model for vacancy-assisted charge transport uses Fermi--Dirac statistics for electrons and holes and Blakemore statistics for the mobile ionic vacancies in the perovskite. Existence of weak solutions and their boundedness was proven in a previous work. For the uniqueness proof, we establish improved integrability of the gradients of the charge-carrier densities. Based on estimates obtained in the previous paper, we consider suitably regularized continuity equations with partly frozen arguments and apply the regularity results for scalar quasilinear elliptic equations by Meinlschmidt & Rehberg, Evolution Equations and Control Theory, 2016, 5(1):147-184. -
D. Abdel, A. Glitzky, M. Liero, Analysis of a drift-diffusion model for perovskite solar cells, Discrete and Continuous Dynamical Systems. Series B. A Journal Bridging Mathematics and Sciences, 30 (2025), pp. 99--131 (appeared online in June 2024), DOI 10.3934/dcdsb.2024081 .
Abstract
This paper deals with the analysis of an instationary drift-diffusion model for perovskite solar cells including Fermi--Dirac statistics for electrons and holes and Blakemore statistics for the mobile ionic vacancies in the perovskite layer. The free energy functional is related to this choice of the statistical relations. Exemplary simulations varying the mobility of the ionic vacancy demonstrate the necessity to include the migration of ionic vacancies in the model frame. To prove the existence of weak solutions, first a problem with regularized state equations and reaction terms on any arbitrarily chosen finite time interval is considered. Its solvability follows from a time discretization argument and passage to the time-continuous limit. Applying Moser iteration techniques, a priori estimates for densities, chemical potentials and the electrostatic potential of its solutions are derived that are independent of the regularization level, which in turn ensure the existence of solutions to the original problem. -
M. O'Donovan, P. Farrell, J. Moatti, T. Streckenbach, Th. Koprucki, S. Schulz, Impact of random alloy fluctuations on the carrier distribution in multi-color (In,Ga)N/GaN quantum well systems, Physical Review Applied, 21 (2024), pp. 024052/1--024052/12, DOI 10.1103/PhysRevApplied.21.024052 .
Abstract
In this work, we study the impact that random alloy fluctuations have on the distribution of electrons and holes across the active region of a (In,Ga)N/GaN multi-quantum well based light emitting diode (LED). To do so, an atomistic tight-binding model is employed to account for alloy fluctuations on a microscopic level and the resulting tight-binding energy landscape forms input to a drift-diffusion model. Here, quantum corrections are introduced via localization landscape theory and we show that when neglecting alloy disorder our theoretical framework yields results similar to commercial software packages that employ a self-consistent Schroedinger-Poisson-drift-diffusion solver. Similar to experimental studies in the literature, we have focused on a multi-quantum well system where two of the three wells have the same In content while the third well differs in In content. By changing the order of wells in this multicolor quantum well structure and looking at the relative radiative recombination rates of the different emitted wavelengths, we (i) gain insight into the distribution of carriers in such a system and (ii) can compare our findings to trends observed in experiment. Our results indicate that the distribution of carriers depends significantly on the treatment of the quantum well microstructure. When including random alloy fluctuations and quantum corrections in the simulations, the calculated trends in the relative radiative recombination rates as a function of the well ordering are consistent with previous experimental studies. The results from the widely employed virtual crystal approximation contradict the experimental data. Overall, our work highlights the importance of a careful and detailed theoretical description of the carrier transport in an (In,Ga)N/GaN multi-quantum well system to ultimately guide the design of the active region of III-N-based LED structures. -
W. Lei, S. Piani, P. Farrell, N. Rotundo, L. Heltai, A weighted hybridizable discontinuous Galerkin method for drift-diffusion problems, Journal of Scientific Computing, 99 (2024), pp. 33/1--33/26, DOI 10.1007/s10915-024-02481-w .
Abstract
In this work we propose a weighted hybridizable discontinuous Galerkin method (W-HDG) for drift-diffusion problems. By using specific exponential weights when computing the L2 product in each cell of the discretization, we are able to mimic the behavior of the Slotboom variables, and eliminate the drift term from the local matrix contributions, while still solving the problem for the primal variables. We show that the proposed numerical scheme is well-posed, and validate numerically that it has the same properties as classical HDG methods, including optimal convergence, and superconvergence of postprocessed solutions. For polynomial degree zero, dimension one, and vanishing HDG stabilization parameter, W-HDG coincides with the Scharfetter--Gummel finite volume scheme (i.e., it produces the same system matrix). The use of local exponential weights generalizes the Scharfetter-Gummel scheme (the state-of-the-art for finite volume discretization of transport dominated problems) to arbitrary high order approximations. -
S. Piani, P. Farrell, W. Lei, N. Rotundo, L. Heltai, Data-driven solutions of ill-posed inverse problems arising from doping reconstruction in semiconductors, Applied Mathematics in Science and Engineering, 32 (2024), pp. 2323626/1--2323626/27, DOI 10.1080/27690911.2024.2323626 .
Abstract
The non-destructive estimation of doping concentrations in semiconductor devices is of paramount importance for many applications ranging from crystal growth, the recent redefinition of the 1kg to defect, and inhomogeneity detection. A number of technologies (such as LBIC, EBIC and LPS) have been developed which allow the detection of doping variations via photovoltaic effects. The idea is to illuminate the sample at several positions and detect the resulting voltage drop or current at the contacts. We model a general class of such photovoltaic technologies by ill-posed global and local inverse problems based on a drift-diffusion system that describes charge transport in a self-consistent electrical field. The doping profile is included as a parametric field. To numerically solve a physically relevant local inverse problem, we present three different data-driven approaches, based on least squares, multilayer perceptrons, and residual neural networks. Our data-driven methods reconstruct the doping profile for a given spatially varying voltage signal induced by a laser scan along the sample's surface. The methods are trained on synthetic data sets (pairs of discrete doping profiles and corresponding photovoltage signals at different illumination positions) which are generated by efficient physics-preserving finite volume solutions of the forward problem. While the linear least square method yields an average absolute l-infinity / displaystyle ell ^infty error around 10%, the nonlinear networks roughly halve this error to 5%, respectively. Finally, we optimize the relevant hyperparameters and test the robustness of our approach with respect to noise. -
D. Abdel, C. Chainais-Hillairet, P. Farrell, M. Herda, Numerical analysis of a finite volume scheme for charge transport in perovskite solar cells, IMA Journal of Numerical Analysis, published online on 10.6.2023, DOI 10.1093/imanum/drad034 .
Abstract
In this paper, we consider a drift-diffusion charge transport model for perovskite solar cells, where electrons and holes may diffuse linearly (Boltzmann approximation) or nonlinearly (e.g. due to Fermi-Dirac statistics). To incorporate volume exclusion effects, we rely on the Fermi-Dirac integral of order −1 when modeling moving anionic vacancies within the perovskite layer which is sandwiched between electron and hole transport layers. After non-dimensionalization, we first prove a continuous entropy-dissipation inequality for the model. Then, we formulate a corresponding two-point flux finite volume scheme on Voronoi meshes and show an analogous discrete entropy-dissipation inequality. This inequality helps us to show the existence of a discrete solution of the nonlinear discrete system with the help of a corollary of Brouwer's fixed point theorem and the minimization of a convex functional. Finally, we verify our theoretically proven properties numerically, simulate a realistic device setup and show exponential decay in time with respect to the L2 error as well as a physically and analytically meaningful relative entropy. -
R. Finn, M. O'Donovan, P. Farrell, J. Moatti, T. Streckenbach, Th. Koprucki, S. Schulz, Theoretical study of the impact of alloy disorder on carrier transport and recombination processes in deep UV (Al,Ga)N light emitters, Applied Physics Letters, 122 (2023), pp. 241104/1--241104/7, DOI 10.1063/5.0148168 .
Abstract
Aluminum gallium nitride [(Al,Ga)N] has gained significant attention in recent years due to its potential for highly efficient light emitters operating in the deep ultra-violet (UV) range (<280 nm). However, given that current devices exhibit extremely low efficiencies, understand- ing the fundamental properties of (Al,Ga)N-based systems is of key importance. Here, using a multi-scale simulation framework, we study the impact of alloy disorder on carrier transport, radiative and non-radiative recombination processes in a c-plane Al 0.7 Ga0.3 N/Al0.8 Ga0.2 N quantum well embedded in a p-n junction. Our calculations reveal that alloy fluctuations can open "percolative" pathways that promote transport for the electrons and holes into the quantum well region. Such an effect is neglected in conventional and widely used transport sim- ulations. Moreover, we find that the resulting increased carrier density and alloy induced carrier localization effects significantly increase non-radiative Auger--Meitner recombination in comparison to the radiative process. Thus, to suppress such non-radiative process and poten- tially related material degradation, a careful design (wider well, multi-quantum wells) of the active region is required to improve the effi- ciency of deep UV light emitters. -
A. Glitzky, M. Liero, A drift-diffusion based electrothermal model for organic thin-film devices including electrical and thermal environment, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, published online on 27.11.2023, DOI 10.1002/zamm.202300376 .
Abstract
We derive and investigate a stationary model for the electrothermal behavior of organic thin-film devices including their electrical and thermal environment. Whereas the electrodes are modeled by Ohm's law, the electronics of the organic device itself is described by a generalized van Roosbroeck system with temperature dependent mobilities and using Gauss--Fermi integrals for the statistical relation. The currents give rise to Joule heat which together with the heat generated by the generation/recombination of electrons and holes in the organic device occur as source terms in the heat flow equation that has to be considered on the whole domain. The crucial task is to establish that the quantities in the transfer conditions at the interfaces between electrodes and the organic semiconductor device have sufficient regularity. Therefore, we restrict the analytical treatment of the system to two spatial dimensions. We consider layered organic structures, where the physical parameters (total densities of transport states, LUMO and HOMO energies, disorder parameter, basic mobilities, activation energies, relative dielectric permittivity, heat conductivity) are piecewise constant. We prove the existence of weak solutions using Schauder's fixed point theorem and a regularity result for strongly coupled systems with nonsmooth data and mixed boundary conditions that is verified by Caccioppoli estimates and a Gehring-type lemma. -
P. Farrell, J. Moatti, M. O'Donovan, S. Schulz, Th. Koprucki, Importance of satisfying thermodynamic consistency in optoelectronic device simulations for high carrier densities, Optical and Quantum Electronics, 55 (2023), pp. 978/1--978/12, DOI 10.1007/s11082-023-05234-5 .
Abstract
We show the importance of using a thermodynamically consistent flux discretization when describing drift-diffusion processes within light emitting diode simulations. Using the classical Scharfetter--Gummel scheme with Fermi--Dirac statistics is an example of such an inconsistent scheme. In this case, for an (In,Ga)N multi quantum well device, the Fermi levels show steep gradients on one side of the quantum wells which are not to be expected. This result originates from neglecting diffusion enhancement associated with Fermi--Dirac statistics in the numerical flux approximation. For a thermodynamically consistent scheme, such as the SEDAN scheme, the spikes in the Fermi levels disappear. We will show that thermodynamic inconsistency has far reaching implications on the current-voltage curves and recombination rates. -
M. O'Donovan, P. Farrell, T. Streckenbach, Th. Koprucki, S. Schulz, Multiscale simulations of uni-polar hole transport in (In,Ga)N quantum well systems, Optical and Quantum Electronics, 54 (2022), pp. 405/1--405/23, DOI 10.1007/s11082-022-03752-2 .
Abstract
Understanding the impact of the alloy micro-structure on carrier transport becomes important when designing III-nitride-based LED structures. In this work, we study the impact of alloy fluctuations on the hole carrier transport in (In,Ga)N single and multi-quantum well systems. To disentangle hole transport from electron transport and carrier recombination processes, we focus our attention on uni-polar (p-i-p) systems. The calculations employ our recently established multi-scale simulation framework that connects atomistic tight-binding theory with a macroscale drift-diffusion model. In addition to alloy fluctuations, we pay special attention to the impact of quantum corrections on hole transport. Our calculations indicate that results from a virtual crystal approximation present an upper limit for the hole transport in a p-i-p structure in terms of the current-voltage characteristics. Thus we find that alloy fluctuations can have a detrimental effect on hole transport in (In,Ga)N quantum well systems, in contrast to uni-polar electron transport. However, our studies also reveal that the magnitude by which the random alloy results deviate from virtual crystal approximation data depends on several factors, e.g. how quantum corrections are treated in the transport calculations. -
A. Glitzky, M. Liero, G. Nika, A coarse-grained electrothermal model for organic semiconductor devices, Mathematical Methods in the Applied Sciences, 45 (2022), pp. 4809--4833, DOI 10.1002/mma.8072 .
Abstract
We derive a coarse-grained model for the electrothermal interaction of organic semiconductors. The model combines stationary drift-diffusion based electrothermal models with thermistor type models on subregions of the device and suitable transmission conditions. Moreover, we prove existence of a solution using a regularization argument and Schauder's fixed point theorem. In doing so, we extend recent work by taking into account the statistical relation given by the Gauss--Fermi integral and mobility functions depending on the temperature, charge-carrier density, and field strength, which is required for a proper description of organic devices. -
TH. Koprucki, A. Maltsi, A. Mielke, Symmetries in transmission electron microscopy imaging of crystals with strain, Proceedings of the Royal Society of Edinburgh. Section A. Mathematics, 478 (2022), pp. 20220317/1--20220317/23, DOI 10.1098/rspa.2022.0317 .
Abstract
TEM images of strained crystals often exhibit symmetries, the source of which is not always clear. To understand these symmetries we distinguish between symmetries that occur from the imaging process itself and symmetries of the inclusion that might affect the image. For the imaging process we prove mathematically that the intensities are invariant under specific transformations. A combination of these invariances with specific properties of the strain profile can then explain symmetries observed in TEM images. We demonstrate our approach to the study of symmetries in TEM images using selected examples in the field of semiconductor nanostructures such as quantum wells and quantum dots. -
D. Abdel, P. Farrell, J. Fuhrmann, Assessing the quality of the excess chemical potential flux scheme for degenerate semiconductor device simulation, Optical and Quantum Electronics, 53 (2021), pp. 163/1--163/10, DOI 10.1007/s11082-021-02803-4 .
Abstract
The van Roosbroeck system models current flows in (non-)degenerate semiconductor devices. Focusing on the stationary model, we compare the excess chemical potential discretization scheme, a flux approximation which is based on a modification of the drift term in the current densities, with another state-of-the-art Scharfetter-Gummel scheme, namely the diffusion-enhanced scheme. Physically, the diffusion-enhanced scheme can be interpreted as a flux approximation which modifies the thermal voltage. As a reference solution we consider an implicitly defined integral flux, using Blakemore statistics. The integral flux refers to the exact solution of a local two point boundary value problem for the continuous current density and can be interpreted as a generalized Scharfetter-Gummel scheme. All numerical discretization schemes can be used within a Voronoi finite volume method to simulate charge transport in (non-)degenerate semiconductor devices. The investigation includes the analysis of Taylor expansions, a derivation of error estimates and a visualization of errors in local flux approximations to extend previous discussions. Additionally, drift-diffusion simulations of a p-i-n device are performed. -
S. Kayser, P. Farrell, N. Rotundo, Detecting striations via the lateral photovoltage scanning method without screening effect, Optical and Quantum Electronics, 53 (2021), pp. 288/1--288/10, DOI 10.1007/s11082-021-02911-1 .
Abstract
The lateral photovoltage scanning method (LPS) detects doping inhomogeneities in semiconductors such as Si, Ge and Si(x)Ge(1-x) in a cheap, fast and nondestructive manner. LPS relies on the bulk photovoltaic effect and thus can detect any physical quantity affecting the band profiles of the sample. LPS finite volume simulation using commercial software suffer from long simulation times and convergence instabilities. We present here an open-source finite volume simulation for a 2D Si sample using the ddfermi simulator. For low injection conditions we show that the LPS voltage is proportional to the doping gradient as previous theory suggested under certain conditions. For higher injection conditions we directly show how the LPS voltage and the doping gradient differ and link the physical effect of lower local resolution to the screening effect. Previously, the loss of local resolution was assumed to be only connected to the enlargement of the excess charge carrier distribution. -
O. Marquardt, Simulating the electronic properties of semiconductor nanostructures using multiband $kcdot p$ models, Computational Materials Science, 194 (2021), pp. 110318/1--110318/11, DOI 10.1016/j.commatsci.2021.110318 .
Abstract
The eight-band $kcdot p$ formalism been successfully applied to compute the electronic properties of a wide range of semiconductor nanostructures in the past and can be considered the backbone of modern semiconductor heterostructure modelling. However, emerging novel material systems and heterostructure fabrication techniques raise questions that cannot be answered using this well-established formalism, due to its intrinsic limitations. The present article reviews recent studies on the calculation of electronic properties of semiconductor nanostructures using a generalized multiband $kcdot p$ approach that allows both the application of the eight-band model as well as more sophisticated approaches for novel material systems and heterostructures. -
D. Chaudhuri, M. O'Donovan, T. Streckenbach, O. Marquardt, P. Farrell, S.K. Patra, Th. Koprucki, S. Schulz, Multiscale simulations of the electronic structure of III-nitride quantum wells with varied indium content: Connecting atomistic and continuum-based models, Journal of Applied Physics, 129 (2021), pp. 073104/1--073104/16, DOI 10.1063/5.0031514 .
-
A. Kirch, A. Fischer, M. Liero, J. Fuhrmann, A. Glitzky, S. Reineke, Electrothermal tristability causes sudden burn-in phenomena in organic LEDs, Advanced Functional Materials, published online in September 2021, DOI 10.1002/adfm.202106716 .
-
A. Glitzky, M. Liero, G. Nika, Analysis of a hybrid model for the electrothermal behavior of semiconductor heterostructures, Journal of Mathematical Analysis and Applications, 507 (2022), pp. 125815/1--125815/26 (published online on 16.11.2021), DOI 10.1016/j.jmaa.2021.125815 .
Abstract
We prove existence of a weak solution for a hybrid model for the electro-thermal behavior of semiconductor heterostructures. This hybrid model combines an electro-thermal model based on drift-diffusion with thermistor type models in different subregions of the semiconductor heterostructure. The proof uses a regularization method and Schauder's fixed point theorem. For boundary data compatible with thermodynamic equilibrium we verify, additionally, uniqueness. Moreover, we derive bounds and higher integrability properties for the electrostatic potential and the quasi Fermi potentials as well as the temperature. -
A. Glitzky, M. Liero, G. Nika, An existence result for a class of electrothermal drift-diffusion models with Gauss--Fermi statistics for organic semiconductors, Analysis and Applications, 19 (2021), pp. 275--304, DOI 10.1142/S0219530519500246 .
Abstract
This work is concerned with the analysis of a drift-diffusion model for the electrothermal behavior of organic semiconductor devices. A "generalized Van Roosbroeck” system coupled to the heat equation is employed, where the former consists of continuity equations for electrons and holes and a Poisson equation for the electrostatic potential, and the latter features source terms containing Joule heat contributions and recombination heat. Special features of organic semiconductors like Gauss--Fermi statistics and mobilities functions depending on the electric field strength are taken into account. We prove the existence of solutions for the stationary problem by an iteration scheme and Schauder's fixed point theorem. The underlying solution concept is related to weak solutions of the Van Roosbroeck system and entropy solutions of the heat equation. Additionally, for data compatible with thermodynamic equilibrium, the uniqueness of the solution is verified. It was recently shown that self-heating significantly influences the electronic properties of organic semiconductor devices. Therefore, modeling the coupled electric and thermal responses of organic semiconductors is essential for predicting the effects of temperature on the overall behavior of the device. This work puts the electrothermal drift-diffusion model for organic semiconductors on a sound analytical basis. -
A. Glitzky, M. Liero, G. Nika, Analysis of a bulk-surface thermistor model for large-area organic LEDs, Portugaliae Mathematica. A Journal of the Portuguese Mathematical Society, 78 (2021), pp. 187--210, DOI 10.4171/PM/2066 .
Abstract
The existence of a weak solution for an effective system of partial differential equations describing the electrothermal behavior of large-area organic light-emitting diodes (OLEDs) is proved. The effective system consists of the heat equation in the three-dimensional bulk glass substrate and two semi-linear equations for the current flow through the electrodes coupled to algebraic equations for the continuity of the electrical fluxes through the organic layers. The electrical problem is formulated on the (curvilinear) surface of the glass substrate where the OLED is mounted. The source terms in the heat equation are due to Joule heating and are hence concentrated on the part of the boundary where the current-flow equation is posed. The existence of weak solutions to the effective system is proved via Schauder's fixed-point theorem. Moreover, since the heat sources are a priori only in $L^1$, the concept of entropy solutions is used. -
P. Farrell, S. Kayser, N. Rotundo, Modeling and simulation of the lateral photovoltage scanning method, Computers & Mathematics with Applications. An International Journal, 102 (2021), pp. 248--260, DOI 10.1016/j.camwa.2021.10.017 .
Abstract
The fast, cheap and nondestructive lateral photovoltage scanning (LPS) method detects inhomogeneities in semiconductors crystals. The goal of this paper is to model and simulate this technique for a given doping profile. Our model is based on the semiconductor device equations combined with a nonlinear boundary condition, modelling a volt meter. To validate our 2D and 3D finite volume simulations, we use theory developed by Tauc [21] to derive three analytical predictions which our simulation results corroborate, even for anisotropic 2D and 3D meshes. Our code runs about two orders of magnitudes faster than earlier implementations based on commercial software [15]. It also performs well for small doping concentrations which previously could not be simulated at all due to numerical instabilities. Our simulations provide experimentalists with reference laser powers for which meaningful voltages can still be measured. For higher laser power the screening effect does not allow this anymore. -
TH. Koprucki, A. Maltsi, A. Mielke, On the Darwin--Howie--Whelan equations for the scattering of fast electrons described by the Schrödinger equation, SIAM Journal on Applied Mathematics, 81 (2021), pp. 1552--1578, DOI 10.1137/21M139164X .
Abstract
The Darwin-Howie-Whelan equations are commonly used to describe and simulate the scattering of fast electrons in transmission electron microscopy. They are a system of infinitely many envelope functions, derived from the Schrödinger equation. However, for the simulation of images only a finite set of envelope functions is used, leading to a system of ordinary differential equations in thickness direction of the specimen. We study the mathematical structure of this system and provide error estimates to evaluate the accuracy of special approximations, like the two-beam and the systematic-row approximation. -
A. Maltsi, T. Niermann, T. Streckenbach, K. Tabelow, Th. Koprucki, Numerical simulation of TEM images for In(Ga)As/GaAs quantum dots with various shapes, Optical and Quantum Electronics, 52 (2020), pp. 257/1--257/11, DOI 10.1007/s11082-020-02356-y .
Abstract
We present a mathematical model and a tool chain for the numerical simulation of TEM images of semiconductor quantum dots (QDs). This includes elasticity theory to obtain the strain profile coupled with the Darwin-Howie-Whelan equations, describing the propagation of the electron wave through the sample. We perform a simulation study on indium gallium arsenide QDs with different shapes and compare the resulting TEM images to experimental ones. This tool chain can be applied to generate a database of simulated TEM images, which is a key element of a novel concept for model-based geometry reconstruction of semiconductor QDs, involving machine learning techniques. -
O. Marquardt, M.A. Caro, Th. Koprucki, P. Mathé, M. Willatzen, Multiband k $cdot$ p model and fitting scheme for ab initio-based electronic structure parameters for wurtzite GaAs, Phys. Rev. B., 101 (2020), pp. 235147/1--235147/12, DOI 10.1103/PhysRevB.101.235147 .
Abstract
We develop a 16-band k · p model for the description of wurtzite GaAs, together with a novel scheme to determine electronic structure parameters for multiband k · p models. Our approach uses low-discrepancy sequences to fit k · p band structures beyond the eight-band scheme to most recent ab initio data, obtained within the framework for hybrid-functional density functional theory with a screened-exchange hybrid functional. We report structural parameters, elastic constants, band structures along high-symmetry lines, and deformation potentials at the Γ point. Based on this, we compute the bulk electronic properties (Γ point energies, effective masses, Luttinger-like parameters, and optical matrix parameters) for a ten-band and a sixteen-band k · p model for wurtzite GaAs. Our fitting scheme can assign priorities to both selected bands and k points that are of particular interest for specific applications. Finally, ellipticity conditions can be taken into account within our fitting scheme in order to make the resulting parameter sets robust against spurious solutions. -
K.M. Gambaryan, T. Boeck, A. Trampert, O. Marquardt, Nucleation chronology and electronic properties of In(As,Sb,P) graded composition quantum dots grown on InAs(100) substrate, ACS Applied Electronic Materials, 2 (2020), pp. 646--650, DOI https://doi.org/10.1021/acsaelm.9b00739 .
Abstract
We provide a detailed study of nucleation process, characterization, electronic and optical properties of graded composition quantum dots (GCQDs) grown from In-As-Sb-P composition liquid phase on an InAs(100) substrate in the Stranski-Krastanov growth mode. Our GCQDs exhibit diameters from 10 to 120 nm and heights from 2 to 20 nm with segregation profiles having a maximum Sb content of approximately 20% at the top and a maximum P content of approximately 15% at the bottom of the GCQDs so that hole confinement is expected in the upper parts of the GCQDs. Using an eight-band k · p model taking strain and built-in electrostatic potentials into account, we have computed the hole ground state energies and charge densities for a wide range of InAs1-x-ySbxPy GCQDs as close as possible to the systems observed in experiment. Finally, we have obtained an absorption spectrum for an ensemble of GCQDs by combining data from both experiment and theory. Excellent agreement between measured and simulated absorption spectra indicates that such GCQDs can be grown following a theory-guided design for application in specific devices. -
C. Cancès, C. Chainais-Hillairet, J. Fuhrmann, B. Gaudeul, A numerical analysis focused comparison of several finite volume schemes for an unipolar degenerated drift-diffusion model, IMA Journal of Numerical Analysis, 41 (2021), pp. 271--314 (published online on 17.07.2020), DOI 10.1093/imanum/draa002 .
Abstract
In this paper, we consider an unipolar degenerated drift-diffusion system where the relation between the concentration of the charged species c and the chemical potential h is h(c) = log c/1-c. We design four different finite volume schemes based on four different formulations of the fluxes. We provide a stability analysis and existence results for the four schemes. The convergence proof with respect to the discretization parameters is established for two of them. Numerical experiments illustrate the behaviour of the different schemes. -
D.H. Doan, A. Fischer, J. Fuhrmann, A. Glitzky, M. Liero, Drift-diffusion simulation of S-shaped current-voltage relations for organic semiconductor devices, Journal of Computational Electronics, 19 (2020), pp. 1164--1174, DOI 10.1007/s10825-020-01505-6 .
Abstract
We present an electrothermal drift-diffusion model for organic semiconductor devices with Gauss-Fermi statistics and positive temperature feedback for the charge carrier mobilities. We apply temperature dependent Ohmic contact boundary conditions for the electrostatic potential and discretize the system by a finite volume based generalized Scharfetter-Gummel scheme. Using path-following techniques we demonstrate that the model exhibits S-shaped current-voltage curves with regions of negative differential resistance, which were only recently observed experimentally. -
A. Kirch, A. Fischer, M. Liero, J. Fuhrmann, A. Glitzky, S. Reineke, Experimental proof of Joule heating-induced switched-back regions in OLEDs, Light: Science and Applications, 9 (2020), pp. 5/1--5/10, DOI 10.1038/s41377-019-0236-9 .
-
J.-P. Köster, A. Putz, H. Wenzel, H.-J. Wünsche, M. Radziunas, H. Stephan, M. Wilkens, A. Zeghuzi, A. Knigge, Mode competition in broad-ridge-waveguide lasers, Semiconductor Science and Technology, 36 (2020), pp. 015014/1--015014/12, DOI 10.1088/1361-6641/abc6e7 .
Abstract
The lateral brightness achievable with high-power GaAs-based laser diodes having long and broad waveguides is commonly regarded to be limited by the onset of higher-order lateral modes. For the study of the lateral-mode competition two complementary simulation tools are applied, representing different classes of approximations. The first tool bases on a completely incoherent superposition of mode intensities and disregards longitudinal effects like spatial hole burning, whereas the second tool relies on a simplified carrier transport and current flow. Both tools yield agreeing power-current characteristics that fit the data measured for 5 to 23 µm wide ridges. Also, a similarly good qualitative conformance of the near and far fields is found. However, the threshold of individual modes, the partition of power between them at a given current, and details of the near and far fields show differences. These differences are the consequence of a high sensitivity of the mode competition to details of the models and of the device structure. Nevertheless, it can be concluded concordantly that the brightness rises with increasing ridge width irrespective of the onset of more and more lateral modes. The lateral brightness 2W · mm¯¹ 1mrad¯¹ at 10MW · cm¯²2 power density on the front facet of the investigated laser with widest ridge (23 µm) is comparable with best values known from much wider broad-area lasers. In addition, we show that one of the simulation tools is able to predict beam steering and coherent beam -
A. Glitzky, M. Liero, G. Nika, Dimension reduction of thermistor models for large-area organic light-emitting diodes, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 3953--3971 (published online on 28.11.2020), DOI 10.3934/dcdss.2020460 .
Abstract
An effective system of partial differential equations describing the heat and current flow through a thin organic light-emitting diode (OLED) mounted on a glass substrate is rigorously derived from a recently introduced fully three-dimensional φ(x)-Laplace thermistor model. The OLED consists of several thin layers that scale differently with respect to the multiscale parameter ε > 0 which is the ratio between the total thickness and the lateral extent of the OLED. Starting point of the derivation is a rescaled formulation of the current-flow equation in the OLED for the driving potential and the heat equation in OLED and glass substrate with Joule heat term concentrated in the OLED. Assuming physically motivated scalings in the electrical flux functions, uniform a priori bounds are derived for the solutions of the three-dimensional system which facilitates the extraction of converging subsequences with limits that are identified as solutions of a dimension reduced system. In the latter, the effective current-flow equation is given by two semilinear equations in the two-dimensional cross-sections of the electrodes and algebraic equations for the continuity of the electrical fluxes through the organic layers. The effective heat equation is formulated only in the glass substrate with Joule heat term on the part of the boundary where the OLED is mounted. -
K. Disser, J. Rehberg, The 3D transient semiconductor equations with gradient-dependent and interfacial recombination, Mathematical Models & Methods in Applied Sciences, 29 (2019), pp. 1819--1851, DOI 10.1142/S0218202519500350 .
Abstract
We establish the well-posedness of the transient van Roosbroeck system in three space dimensions under realistic assumptions on the data: non-smooth domains, discontinuous coefficient functions and mixed boundary conditions. Moreover, within this analysis, recombination terms may be concentrated on surfaces and interfaces and may not only depend on charge-carrier densities, but also on the electric field and currents. In particular, this includes Avalanche recombination. The proofs are based on recent abstract results on maximal parabolic and optimal elliptic regularity of divergence-form operators. -
D.H. Doan, A. Glitzky, M. Liero, Analysis of a drift-diffusion model for organic semiconductor devices, Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 70 (2019), pp. 55/1--55/18, DOI 10.1007/s00033-019-1089-z .
Abstract
We discuss drift-diffusion models for charge-carrier transport in organic semiconductor devices. The crucial feature in organic materials is the energetic disorder due to random alignment of molecules and the hopping transport of carriers between adjacent energetic sites. The former leads to so-called Gauss-Fermi statistics, which describe the occupation of energy levels by electrons and holes. The latter gives rise to complicated mobility models with a strongly nonlinear dependence on temperature, density of carriers, and electric field strength. We present the state-of-the-art modeling of the transport processes and provide a first existence result for the stationary drift-diffusion model taking all of the peculiarities of organic materials into account. The existence proof is based on Schauder's fixed-point theorem. -
M. Kantner, Generalized Scharfetter--Gummel schemes for electro-thermal transport in degenerate semiconductors using the Kelvin formula for the Seebeck coefficient, Journal of Computational Physics, published online on 07.11.2019, urlhttps://doi.org/10.1016/j.jcp.2019.109091, DOI 10.1016/j.jcp.2019.109091 .
Abstract
Many challenges faced in today's semiconductor devices are related to self-heating phenomena. The optimization of device designs can be assisted by numerical simulations using the non-isothermal drift-diffusion system, where the magnitude of the thermoelectric cross effects is controlled by the Seebeck coefficient. We show that the model equations take a remarkably simple form when assuming the so-called Kelvin formula for the Seebeck coefficient. The corresponding heat generation rate involves exactly the three classically known self-heating effects, namely Joule, recombination and Thomson--Peltier heating, without any further (transient) contributions. Moreover, the thermal driving force in the electrical current density expressions can be entirely absorbed in the (nonlinear) diffusion coefficient via a generalized Einstein relation. The efficient numerical simulation relies on an accurate and robust discretization technique for the fluxes (finite volume Scharfetter--Gummel method), which allows to cope with the typically stiff solutions of the semiconductor device equations. We derive two non-isothermal generalizations of the Scharfetter--Gummel scheme for degenerate semiconductors (Fermi--Dirac statistics) obeying the Kelvin formula. The approaches differ in the treatment of degeneration effects: The first is based on an approximation of the discrete generalized Einstein relation implying a specifically modified thermal voltage, whereas the second scheme follows the conventionally used approach employing a modified electric field. We present a detailed analysis and comparison of both schemes, indicating a superior performance of the modified thermal voltage scheme. -
I. Selmer, A.-S. Behnecke, P. Farrell, A. Bueno, P. Gurikov, I. Smirnova, Model development for sc-drying kinetics of aerogels: Part 2. Packed bed of spherical particles, The Journal of Supercritical Fluids, 147 (2019), pp. 147/149--147/161, DOI https://doi.org/10.1016/j.supflu.2018.07.006 .
Abstract
We apply here the previously developed mass transfer model (Part 1) for drying of aerogel monoliths to the supercritical drying of particles in a packed bed. We analyzed the influence of the operating conditions, flow rate, particle and autoclave size on the drying time and consumption of carbon dioxide. Although the model requires certain improvement to quantitatively predict the experimental drying kinetics, it captures all features of the supercritical drying: (i) transition of the limiting mass transfer step between diffusion in the gel and convection in the bulk fluid; (ii) role of CO2 density as natural variable for analysis of the CO2 consumption; (iii) influence of the autoclave dimensions on the drying process. We suggest a unified approach towards the analysis of drying process based on a dimensionless number. Practical recommendations on the rational selection of process parameters to achieve appropriate combinations of drying time and CO2 consumption are formulated. -
Y. Zheng, A. Fischer, M. Sawatzki, D.H. Doan, M. Liero, A. Glitzky, S. Reineke, S.C.B. Mannsfeld, Introducing pinMOS memory: A novel, non-volatile organic memory device, Advanced Functional Materials, 30 (2020), pp. 1907119/1--1907119/10 (published online on 07.11.2019), DOI 10.1002/adfm.201907119 .
Abstract
In recent decades, organic memory devices have been researched intensely and they can, among other application scenarios, play an important role in the vision of an internet of things. Most studies concentrate on storing charges in electronic traps or nanoparticles while memory types where the information is stored in the local charge up of an integrated capacitance and presented by capacitance received far less attention. Here, a new type of programmable organic capacitive memory called p-i-n-metal-oxide-semiconductor (pinMOS) memory is demonstrated with the possibility to store multiple states. Another attractive property is that this simple, diode-based pinMOS memory can be written as well as read electrically and optically. The pinMOS memory device shows excellent repeatability, an endurance of more than 104 write-read-eraseread cycles, and currently already over 24 h retention time. The working mechanism of the pinMOS memory under dynamic and steady-state operations is investigated to identify further optimization steps. The results reveal that the pinMOS memory principle is promising as a reliable capacitive memory device for future applications in electronic and photonic circuits like in neuromorphic computing or visual memory systems. -
L. Adam, M. Hintermüller, D. Peschka, Th.M. Surowiec, Optimization of a multiphysics problem in semiconductor laser design, SIAM Journal on Applied Mathematics, 79 (2019), pp. 257--283, DOI 10.1137/18M1179183 .
Abstract
A multimaterial topology optimization framework is suggested for the simultaneous optimization of mechanical and optical properties to be used in the development of optoelectronic devices. Based on the physical aspects of the underlying device, a nonlinear multiphysics model for the elastic and optical properties is proposed. Rigorous proofs are provided for the sensitivity of the fundamental mode of the device with respect to the changes in the underlying topology. After proving existence and optimality results, numerical experiments leading to an optimal material distribution for maximizing the strain in a Ge-on-Si microbridge are given. The highly favorable electronic properties of this design are demonstrated by steady-state simulations of the corresponding van Roosbroeck (drift-diffusion) system. -
L. Heltai, N. Rotundo, Error estimates in weighted Sobolev norms for finite element immersed interface methods, Computers & Mathematics with Applications. An International Journal, 78 (2019), pp. 3586--3604, DOI 10.1016/j.camwa.2019.05.029 .
Abstract
When solving elliptic partial differential equations in a region containing immersed interfaces (possibly evolving in time), it is often desirable to approximate the problem using an independent background discretisation, not aligned with the interface itself. Optimal convergence rates are possible if the discretisation scheme is enriched by allowing the discrete solution to have jumps aligned with the surface, at the cost of a higher complexity in the implementation. A much simpler way to reformulate immersed interface problems consists in replacing the interface by a singular force field that produces the desired interface conditions, as done in immersed boundary methods. These methods are known to have inferior convergence properties, depending on the global regularity of the solution across the interface, when compared to enriched methods. In this work we prove that this detrimental effect on the convergence properties of the approximate solution is only a local phenomenon, restricted to a small neighbourhood of the interface. In particular we show that optimal approximations can be constructed in a natural and inexpensive way, simply by reformulating the problem in a distributionally consistent way, and by resorting to weighted norms when computing the global error of the approximation. -
J. Lähnemann, M.O. Hill, J. Herranz, O. Marquardt, G. Gao, A. Al Hassan, A. Davtyan, S.O. Hruszkewycz, M.V. Holt, Ch. Huang, I. Calvo-Almazán, U. Jahn, U. Pietsch, L.J. Lauhon, L. Geelhaar, Correlated nanoscale analysis of the emission from wurtzite versus zincblende (In,Ga)As/GaAs nanowire core-shell quantum wells, ACS Nano, 19 (2019), pp. 4448--4457, DOI 10.1021/acs.nanolett.9b01241 .
Abstract
While the properties of wurtzite GaAs have been extensively studied during the past decade, little is known about the influence of the crystal polytype on ternary (In,Ga)As quantum well structures. We address this question with a unique combination of correlated, spatially resolved measurement techniques on core-shell nanowires that contain extended segments of both the zincblende and wurtzite polytypes. Cathodoluminescence hyperspectral imaging reveals a blue-shift of the quantum well emission energy by 75 ± 15 meV in the wurtzite polytype segment. Nanoprobe X-ray diffraction and atom probe tomography enable k•p calculations for the specific sample geometry to reveal two comparable contributions to this shift. First, there is a 30% drop in In mole fraction going from the zincblende to the wurtzite segment. Second, the quantum well is under compressive strain, which has a much stronger impact on the hole ground state in the wurtzite than in the zincblende segment. Our results highlight the role of the crystal structure in tuning the emission of (In,Ga)As quantum wells and pave the way to exploit the possibilities of three-dimensional band gap engineering in core-shell nanowire heterostructures. At the same time, we have demonstrated an advanced characterization toolkit for the investigation of semiconductor nanostructures. -
A. Glitzky, M. Liero, Instationary drift-diffusion problems with Gauss--Fermi statistics and field-dependent mobility for organic semiconductor devices, Communications in Mathematical Sciences, 17 (2019), pp. 33--59, DOI 10.4310/cms.2019.v17.n1.a2 .
Abstract
This paper deals with the analysis of an instationary drift-diffusion model for organic semiconductor devices including Gauss--Fermi statistics and application-specific mobility functions. The charge transport in organic materials is realized by hopping of carriers between adjacent energetic sites and is described by complicated mobility laws with a strong nonlinear dependence on temperature, carrier densities and the electric field strength. To prove the existence of global weak solutions, we consider a problem with (for small densities) regularized state equations on any arbitrarily chosen finite time interval. We ensure its solvability by time discretization and passage to the time-continuous limit. Positive lower a priori estimates for the densities of its solutions that are independent of the regularization level ensure the existence of solutions to the original problem. Furthermore, we derive for these solutions global positive lower and upper bounds strictly below the density of transport states for the densities. The estimates rely on Moser iteration techniques. -
P. Farrell, D. Peschka, Nonlinear diffusion, boundary layers and nonsmoothness: Analysis of challenges in drift-diffusion semiconductor simulations, Computers & Mathematics with Applications. An International Journal, 78 (2019), pp. 3731--3747, DOI 10.1016/j.camwa.2019.06.007 .
Abstract
We analyze and benchmark the error and the convergence order of finite difference, finite-element as well as Voronoi finite-volume discretization schemes for the drift-diffusion equations describing charge transport in bulk semiconductor devices. Three common challenges, that can corrupt the precision of numerical solutions, will be discussed: boundary layers at Ohmic contacts, discontinuties in the doping profile, and corner singularities in L-shaped domains. The influence on the order of convergence is assessed for each computational challenge and the different discretization schemes. Additionally, we provide an analysis of the inner boundary layer asymptotics near Ohmic contacts to support our observations. -
D. Peschka, N. Rotundo, M. Thomas, Doping optimization for optoelectronic devices, Optical and Quantum Electronics, 50 (2018), pp. 125/1--125/9, DOI 10.1007/s11082-018-1393-4 .
Abstract
We present a mathematical and numerical framework for the optimal design of doping profiles for optoelectronic devices using methods from mathematical optimization. With the goal to maximize light emission and reduce the threshold of an edge-emitting laser, we consider a drift-diffusion model for charge transport and include modal gain and total current into a cost functional, which we optimize in cross sections of the emitter. We present 1D and 2D results for exemplary setups that point out possible routes for device improvement. -
A.W. Achtstein, O. Marquardt, R. Scott, M. Ibrahim, Th. Riedl, A.V. Prudnikau, A. Antanovich, N. Owchimikow, J.K.N. Lindner, M. Artemyev, U. Woggon, Impact of shell growth on recombination dynamics and exciton-phonon interaction in CdSe-CdS core-shell nanoplatelets, ACS Nano, 12 (2018), pp. 9476--9483, DOI 10.1021/acsnano.8b04803 .
-
A. Fischer, M. Pfalz, K. Vandewal, M. Liero, A. Glitzky, S. Lenk, S. Reineke, Full electrothermal OLED model including nonlinear self-heating effects, Physical Review Applied, 10 (2018), pp. 014023/1--014023/12, DOI 10.1103/PhysRevApplied.10.014023 .
Abstract
Organic light-emitting diodes (OLEDs) are widely studied semiconductor devices for which a simple description by a diode equation typically fails. In particular, a full description of the current-voltage relation, including temperature effects, has to take the low electrical conductivity of organic semiconductors into account. Here, we present a temperature-dependent resistive network, incorporating recombination as well as electron and hole conduction to describe the current-voltage characteristics of an OLED over the entire operation range. The approach also reproduces the measured nonlinear electrothermal feedback upon Joule self-heating in a self-consistent way. Our model further enables us to learn more about internal voltage losses caused by the charge transport from the contacts to the emission layer which is characterized by a strong temperature-activated electrical conductivity, finally determining the strength of the electrothermal feedback. In general, our results provide a comprehensive picture to understand the electrothermal operation of an OLED which will be essential to ensure and predict especially long-term stability and reliability in superbright OLED applications. -
J. Haskovec, S. Hittmeir, P. Markowich, A. Mielke, Decay to equilibrium for energy-reaction-diffusion systems, SIAM Journal on Mathematical Analysis, 50 (2018), pp. 1037--1075, DOI 10.1137/16M1062065 .
Abstract
We derive thermodynamically consistent models of reaction-diffusion equations coupled to a heat equation. While the total energy is conserved, the total entropy serves as a driving functional such that the full coupled system is a gradient flow. The novelty of the approach is the Onsager structure, which is the dual form of a gradient system, and the formulation in terms of the densities and the internal energy. In these variables it is possible to assume that the entropy density is strictly concave such that there is a unique maximizer (thermodynamical equilibrium) given linear constraints on the total energy and suitable density constraints. We consider two particular systems of this type, namely, a diffusion-reaction bipolar energy transport system, and a drift-diffusion-reaction energy transport system with confining potential. We prove corresponding entropy-entropy production inequalities with explicitely calculable constants and establish the convergence to thermodynamical equilibrium, at first in entropy and further in L1 using Cziszar-Kullback-Pinsker type inequalities. -
F.M. Sawatzki, D.H. Doan, H. Kleemann, M. Liero, A. Glitzky, Th. Koprucki, K. Leo, Balance of horizontal and vertical charge transport in organic field-effect transistors, Physical Review Applied, 10 (2018), pp. 034069/1--034069/10, DOI 10.1103/PhysRevApplied.10.034069 .
Abstract
High-performance organic field-effect transistors (OFETs) are an essential building block for future flexible electronics. Although there has been steady progress in the development of high-mobility organic semiconductors, the performance of lateral state-of-the-art OFETs still falls short, especially with regard to the transition frequency. One candidate to overcome the shortcomings of the lateral OFET is its vertical embodiment, the vertical organic field-effect transistor (VOFET). However, the detailed mechanism of VOFET operation is poorly understood and a matter of discussion. Proposed descriptions of the formation and geometry of the vertical channel vary significantly. In particular, values for lateral depth of the vertical channel reported so far show a large variation. This is an important question for the transistor integration, though, since a channel depth in the micrometer range would severely limit the possible integration density. Here, we investigate charge transport in such VOFETs via drift-diffusion simulations and experimental measurements. We use a (vertical) organic light-emitting transistor ((V)OLET) as a means to map the spatial distribution of charge transport within the vertical channel. Comparing simulation and experiment, we can conclusively describe the operation mechanism which is mainly governed by an accumulation of charges at the dielectric interface and the channel formation directly at the edge of the source electrode. In particular, we quantitatively describe how the channel depth depends on parameters such as gate-source voltage, drain-source voltage, and lateral and vertical mobility. Based on the proposed operation mechanism, we derive an analytical estimation for the lateral dimensions of the channel, helping to predict an upper limit for the integration density of VOFETs. -
P. Corfdir, H. Li, O. Marquardt, G. Gao, M.R. Molas, J.K. Zettler, D. VAN Treeck, T. Flissikowski, M. Potemski, C. Draxl, A. Trampert, S. Fernández-Garrido, H.T. Grahn, O. Brandt, Crystal-phase quantum wires: One-dimensional heterostructures with atomically flat interfaces, Nano Letters, 18 (2018), pp. 247--254, DOI 10.1021/acs.nanolett.7b03997 .
-
P. Corfdir, O. Marquardt, R.B. Lewis , Ch. Sinito, M. Ramsteiner, A. Trampert, U. Jahn, L. Geelhaar, O. Brandt, W.M. Fomin, Excitonic Aharonov--Bohm oscillations in core-shell nanowires, Advanced Materials, 31 (2019), pp. 1805645/1--1805645/6 (published online on 20.11.2018), DOI 10.1002/adma.201805645 .
-
P. Farrell, M. Patriarca, J. Fuhrmann, Th. Koprucki, Comparison of thermodynamically consistent charge carrier flux discretizations for Fermi--Dirac and Gauss--Fermi statistics, Optical and Quantum Electronics, 50 (2018), pp. 101/1--101/10, DOI 10.1007/s11082-018-1349-8 .
Abstract
We compare three thermodynamically consistent Scharfetter--Gummel schemes for different distribution functions for the carrier densities, including the Fermi--Dirac integral of order 1/2 and the Gauss--Fermi integral. The most accurate (but unfortunately also most costly) generalized Scharfetter--Gummel scheme requires the solution of an integral equation. We propose a new method to solve this integral equation numerically based on Gauss quadrature and Newton's method. We discuss the quality of this approximation and plot the resulting currents for Fermi--Dirac and Gauss--Fermi statistics. Finally, by comparing two modified (diffusion-enhanced and inverse activity based) Scharfetter--Gummel schemes with the more accurate generalized scheme, we show that the diffusion-enhanced ansatz leads to considerably lower flux errors, confirming previous results (J. Comp. Phys. 346:497-513, 2017). -
P. Farrell, A. Linke, Uniform second order convergence of a complete flux scheme on unstructured 1D grids for a singularly perturbed advection-diffusion equation and some multidimensional extensions, Journal of Scientific Computing, 72 (2017), pp. 373--395, DOI 10.1007/s10915-017-0361-7 .
Abstract
The accurate and efficient discretization of singularly perturbed advection-diffusion equations on arbitrary 2D and 3D domains remains an open problem. An interesting approach to tackle this problem is the complete flux scheme (CFS) proposed by G. D. Thiart and further investigated by J. ten Thije Boonkkamp. For the CFS, uniform second order convergence has been proven on structured grids. We extend a version of the CFS to unstructured grids for a steady singularly perturbed advection-diffusion equation. By construction, the novel finite volume scheme is nodally exact in 1D for piecewise constant source terms. This property allows to use elegant continuous arguments in order to prove uniform second order convergence on unstructured one-dimensional grids. Numerical results verify the predicted bounds and suggest that by aligning the finite volume grid along the velocity field uniform second order convergence can be obtained in higher space dimensions as well. -
M. Kantner, M. Mittnenzweig, Th. Koprucki, Hybrid quantum-classical modeling of quantum dot devices, Phys. Rev. B., 96 (2017), pp. 205301/1--205301/17, DOI 10.1103/PhysRevB.96.205301 .
Abstract
The design of electrically driven quantum dot devices for quantum optical applications asks for modeling approaches combining classical device physics with quantum mechanics. We connect the well-established fields of semi-classical semiconductor transport theory and the theory of open quantum systems to meet this requirement. By coupling the van Roosbroeck system with a quantum master equation in Lindblad form, we obtain a new hybrid quantum-classical modeling approach, which enables a comprehensive description of quantum dot devices on multiple scales: It allows the calculation of quantum optical figures of merit and the spatially resolved simulation of the current flow in realistic semiconductor device geometries in a unified way. We construct the interface between both theories in such a way, that the resulting hybrid system obeys the fundamental axioms of (non-)equilibrium thermodynamics. We show that our approach guarantees the conservation of charge, consistency with the thermodynamic equilibrium and the second law of thermodynamics. The feasibility of the approach is demonstrated by numerical simulations of an electrically driven single-photon source based on a single quantum dot in the stationary and transient operation regime. -
O. Marquardt, Th. Krause, V. Kaganer, J. Martin-Sánchez, M. Hanke, O. Brandt, Influence of strain relaxation in axial $In_xGa_1-xN/GaN$ nanowire heterostructures on their electronic properties, Nanotechnology, 28 (2017), pp. 215204/1--215204/6, DOI 10.1088/1361-6528/aa6b73 .
Abstract
We present a systematic theoretical study of the influence of elastic strain relaxation on the built-in electrostatic potentials and the electronic properties of axial InxGa1-xN/GaN nanowire (NW) heterostructures. Our simulations reveal that for a sufficiently large ratio between the thickness of the InxGa1-xN disk and the diameter of the NW, the elastic relaxation leads to a significant reduction of the built-in electrostatic potential in comparison to a planar system of similar layer thickness and In content. In this case, the ground state transition energies approach constant values with increasing thickness of the disk and only depend on the In content, a behavior usually associated to that of a quantum well free of built-in electrostatic potentials. We show that the structures under consideration are by no means field-free, and the built-in potentials continue to play an important role even for ultrathin NWs. In particular, strain and the resulting polarization potentials induce complex confinement features of electrons and holes, which depend on the In content, shape, and dimensions of the heterostructure. -
O. Marquardt, M. Ramsteiner, P. Corfdir, L. Geelhaar, O. Brandt, Modeling the electronic properties of GaAs polytype nanostructures: Impact of strain on the conduction band character, Phys. Rev. B., 95 (2017), pp. 245309/1--245309/8, DOI 10.1103/PhysRevB.95.245309 .
Abstract
We study the electronic properties of GaAs nanowires composed of both the zinc-blende and wurtzite modifications using a ten-band k-p model. In the wurtzite phase, two energetically close conduction bands are of importance for the confinement and the energy levels of the electron ground state. These bands form two intersecting potential landscapes for electrons in zinc-blende/wurtzite nanostructures. The energy difference between the two bands depends sensitively on strain, such that even small strains can reverse the energy ordering of the two bands. This reversal may already be induced by the non-negligible lattice mismatch between the two crystal phases in polytype GaAs nanostructures, a fact that was ignored in previous studies of these structures. We present a systematic study of the influence of intrinsic and extrinsic strain on the electron ground state for both purely zinc-blende and wurtzite nanowires as well as for polytype superlattices. The coexistence of the two conduction bands and their opposite strain dependence results in complex electronic and optical properties of GaAs polytype nanostructures. In particular, both the energy and the polarization of the lowest intersubband transition depends on the relative fraction of the two crystal phases in the nanowire. -
M. Mittnenzweig, A. Mielke, An entropic gradient structure for Lindblad equations and couplings of quantum systems to macroscopic models, Journal of Statistical Physics, 167 (2017), pp. 205--233, DOI 10.1007/s10955-017-1756-4 .
Abstract
We show that all Lindblad operators (i.e. generators of quantum semigroups) on a finite-dimensional Hilbert space satisfying the detailed balance condition with respect to the thermal equilibrium state can be written as a gradient system with respect to the relative entropy. We discuss also thermodynamically consistent couplings to macroscopic systems, either as damped Hamiltonian systems with constant temperature or as GENERIC systems. -
M. Sawatzki, A.A. Hauke, D.H. Doan, P. Formanek, D. Kasemann, Th. Koprucki, K. Leo, On razors edge: Influence of the source insulator edge on the charge transport of vertical organic field effect transistors, MRS Advances, 2 (2017), pp. 1249--1257, DOI 10.1557/adv.2017.29 .
Abstract
To benefit from the many advantages of organic semiconductors like flexibility, transparency, and small thickness, electronic devices should be entirely made from organic materials. This means, additionally to organic LEDs, organic solar cells, and organic sensors, we need organic transistors to amplify, process, and control signals and electrical power. The standard lateral organic field effect transistor (OFET) does not offer the necessary performance for many of these applications. One promising candidate for solving this problem is the vertical organic field effect transistor (VOFET). In addition to the altered structure of the electrodes, the VOFET has one additional part compared to the OFET -- the source-insulator. However, the influence of the used material, the size, and geometry of this insulator on the behavior of the transistor has not yet been examined. We investigate key-parameters of the VOFET with different source insulator materials and geometries. We also present transmission electron microscopy (TEM) images of the edge area. Additionally, we investigate the charge transport in such devices using drift-diffusion simulations and the concept of a vertical organic light emitting transistor (VOLET). The VOLET is a VOFET with an embedded OLED. It allows the tracking of the local current density by measuring the light intensity distribution.
We show that the insulator material and thickness only have a small influence on the performance, while there is a strong impact by the insulator geometry -- mainly the overlap of the insulator into the channel. By tuning this overlap, on/off-ratios of 9x105 without contact doping are possible, -
A. Glitzky, M. Liero, Analysis of p(x)-Laplace thermistor models describing the electrothermal behavior of organic semiconductor devices, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 34 (2017), pp. 536--562.
Abstract
We study a stationary thermistor model describing the electrothermal behavior of organic semiconductor devices featuring non-Ohmic current-voltage laws and self-heating effects. The coupled system consists of the current-flow equation for the electrostatic potential and the heat equation with Joule heating term as source. The self-heating in the device is modeled by an Arrhenius-like temperature dependency of the electrical conductivity. Moreover, the non-Ohmic electrical behavior is modeled by a power law such that the electrical conductivity depends nonlinearly on the electric field. Notably, we allow for functional substructures with different power laws, which gives rise to a $p(x)$-Laplace-type problem with piecewise constant exponent. We prove the existence and boundedness of solutions in the two-dimensional case. The crucial point is to establish the higher integrability of the gradient of the electrostatic potential to tackle the Joule heating term. The proof of the improved regularity is based on Caccioppoli-type estimates, Poincaré inequalities, and a Gehring-type Lemma for the $p(x)$-Laplacian. Finally, Schauder's fixed-point theorem is used to show the existence of solutions. -
A. Caiazzo, F. Caforio, G. Montecinos, L.O. Müller, P.J. Blanco, E.F. Toro, Assessment of reduced order Kalman filter for parameter identification in one-dimensional blood flow models using experimental data, International Journal of Numerical Methods in Biomedical Engineering, 33 (2017), pp. e2843/1--e2843/26, DOI 10.1002/cnm.2843 .
Abstract
This work presents a detailed investigation of a parameter estimation approach based on the reduced order unscented Kalman filter (ROUKF) in the context of one-dimensional blood flow models. In particular, the main aims of this study are (i) to investigate the effect of using real measurements vs. synthetic data (i.e., numerical results of the same in silico model, perturbed with white noise) for the estimation and (ii) to identify potential difficulties and limitations of the approach in clinically realistic applications in order to assess the applicability of the filter to such setups. For these purposes, our numerical study is based on the in vitro model of the arterial network described by [Alastruey et al. 2011, J. Biomech. bf 44], for which experimental flow and pressure measurements are available at few selected locations. In order to mimic clinically relevant situations, we focus on the estimation of terminal resistances and arterial wall parameters related to vessel mechanics (Young's modulus and thickness) using few experimental observations (at most a single pressure or flow measurement per vessel). In all cases, we first perform a theoretical identifiability analysis based on the generalized sensitivity function, comparing then the results obtained with the ROUKF, using either synthetic or experimental data, to results obtained using reference parameters and to available measurements. -
P. Farrell, Th. Koprucki, J. Fuhrmann, Computational and analytical comparison of flux discretizations for the semiconductor device equations beyond Boltzmann statistics, Journal of Computational Physics, 346 (2017), pp. 497--513, DOI 10.1016/j.jcp.2017.06.023 .
Abstract
For a Voronoï finite volume discretization of the van Roosbroeck system with general charge carrier statistics we compare three thermodynamically consistent numerical fluxes known in the literature. We discuss an extension of the Scharfetter--Gummel scheme to non-Boltzmann (e.g. Fermi--Dirac) statistics. It is based on the analytical solution of a two-point boundary value problem obtained by projecting the continuous differential equation onto the interval between neighboring collocation points. Hence, it serves as a reference flux. The exact solution of the boundary value problem can be approximated by computationally cheaper fluxes which modify certain physical quantities. One alternative scheme averages the nonlinear diffusion (caused by the non-Boltzmann nature of the problem), another one modifies the effective density of states. To study the differences between these three schemes, we analyze the Taylor expansions, derive an error estimate, visualize the flux error and show how the schemes perform for a carefully designed p-i-n benchmark simulation. We present strong evidence that the flux discretization based on averaging the nonlinear diffusion has an edge over the scheme based on modifying the effective density of states. -
M. Liero, J. Fuhrmann, A. Glitzky, Th. Koprucki, A. Fischer, S. Reineke, 3D electrothermal simulations of organic LEDs showing negative differential resistance, Optical and Quantum Electronics, 49 (2017), pp. 330/1--330/8, DOI 10.1007/s11082-017-1167-4 .
Abstract
Organic semiconductor devices show a pronounced interplay between temperature-activated conductivity and self-heating which in particular causes inhomogeneities in the brightness of large-area OLEDs at high power. We consider a 3D thermistor model based on partial differential equations for the electrothermal behavior of organic devices and introduce an extension to multiple layers with nonlinear conductivity laws, which also take the diode-like behavior in recombination zones into account. We present a numerical simulation study for a red OLED using a finite-volume approximation of this model. The appearance of S-shaped current-voltage characteristics with regions of negative differential resistance in a measured device can be quantitatively reproduced. Furthermore, this simulation study reveals a propagation of spatial zones of negative differential resistance in the electron and hole transport layers toward the contact. -
M. Kantner, Th. Koprucki, Numerical simulation of carrier transport in semiconductor devices at cryogenic temperatures, Optical and Quantum Electronics, 48 (2016), pp. 543/1--543/7, DOI 10.1007/s11082-016-0817-2 .
Abstract
At cryogenic temperatures the electron?hole plasma in semiconductors becomes strongly degenerate, leading to very sharp internal layers, extreme depletion in intrinsic domains and strong nonlinear diffusion. As a result, the numerical simulation of the drift?diffusion system suffers from serious convergence issues using standard methods. We consider a one-dimensional p-i-n diode to illustrate these problems and present a simple temperature-embedding scheme to enable the numerical simulation at cryogenic temperatures. The method is suitable for forward-biased devices as they appear e.g. in optoelectronic applications. Moreover, the method can be applied to wide band gap semiconductors where similar numerical issues occur already at room temperature. -
M. Kantner, U. Bandelow, Th. Koprucki, J.-H. Schulze, A. Strittmatter, H.-J. Wünsche, Efficient current injection into single quantum dots through oxide-confined pn-diodes, IEEE Transactions on Electron Devices, 63 (2016), pp. 2036--2042.
Abstract
Current injection into single quantum dots embedded in vertical pn-diodes featuring oxide apertures is analyzed in the low-injection regime suitable for single-photon emitters. Experimental and theoretical evidence is found for a rapid lateral spreading of the carriers after passing the oxide aperture in the conventional pin-design. By an alternative design employing p-doping up to the oxide aperture the current spreading can be suppressed resulting in an enhanced current confinement and increased injection efficiencies, both, in the continuous wave and under pulsed excitation. -
D. Peschka, M. Thomas, A. Glitzky, R. Nürnberg, M. Virgilio, S. Guha, Th. Schröder, G. Cappellini, Th. Koprucki, Robustness analysis of a device concept for edge-emitting lasers based on strained germanium, Optical and Quantum Electronics, 48 (2016), pp. 156/1--156/7, DOI 10.1007/s11082-016-0394-4 .
Abstract
We consider a device concept for edge-emitting lasers based on strained germanium microstrips. The device features an inhomogeneous tensile strain distribution generated by a SiN stressor deposited on top of the Ge microstrip. This geometry requires a lateral contact scheme and hence a full two-dimensional description. The two-dimensional simulations of the carrier transport and of the optical field, carried out in a cross section of the device orthogonal to the optical cavity, use microscopic calculations of the strained Ge material gain as an input. In this paper we study laser performance and robustness against Shockley-Read-Hall lifetime variations and device sensitivity to different strain distributions. -
D. Peschka, N. Rotundo, M. Thomas, Towards doping optimization of semiconductor lasers, Journal of Computational and Theoretical Transport, 45 (2016), pp. 410--423.
Abstract
We discuss analytical and numerical methods for the optimization of optoelectronic devices by performing optimal control of the PDE governing the carrier transport with respect to the doping profile. First, we provide a cost functional that is a sum of a regularization and a contribution, which is motivated by the modal net gain that appears in optoelectronic models of bulk or quantum-well lasers. Then, we state a numerical discretization, for which we study optimized solutions for different regularizations and for vanishing weights. -
A. Bercegol, B. Chacko, R. Klenk, I. Lauermann, M.Ch. Lux-Steiner, M. Liero, Point contacts at the copper-indium-gallium-selenide interface -- A theoretical outlook, Journal of Applied Physics, 119 (2016), pp. 155304/1--155304/7, DOI 10.1063/1.4947267 .
Abstract
For a long time, it has been assumed that recombination in the space-charge region of CIGS is dominant, at least in high efficiency solar cells with low band gap. The recent developments like KF post deposition treatment and point-contact junction may call this into question. In this work a theoretical outlook is made using three-dimensional simulations to investigate the effect of pointcontact openings through a passivation layer on CIGS solar cell performance. A large set of solar cells is modeled under different scenarios for the charged defect levels and density, radius of the openings, interface quality and conduction band offset. The positive surface charge created by the passivation layer induces band bending and this influences the contact (CdS) properties, making it beneficial for the open circuit voltage and efficiency, and the effect is even more pronounced when coverage area is more than 95 %, and also makes a positive impact on the device performance, even in the presence of a spike at CIGS/CdS heterojunction. -
F. Kaschura, A. Fischer, M.P. Klinger, D.H. Doan, Th. Koprucki, A. Glitzky, D. Kasemann, J. Widmer, K. Leo, Operation mechanism of high performance organic permeable base transistors with an insulated and perforated base electrode, Journal of Applied Physics, 120 (2016), pp. 094501/1--094501/8, DOI 10.1063/1.4962009 .
-
TH. Koprucki, N. Rotundo, P. Farrell, D.H. Doan, J. Fuhrmann, On thermodynamic consistency of a Scharfetter--Gummel scheme based on a modified thermal voltage for drift-diffusion equations with diffusion enhancement, Optical and Quantum Electronics, 47 (2015), pp. 1327--1332.
Abstract
Driven by applications like organic semiconductors there is an increased interest in numerical simulations based on drift-diffusion models with arbitrary statistical distribution functions. This requires numerical schemes that preserve qualitative properties of the solutions, such as positivity of densities, dissipativity and consistency with thermodynamic equilibrium. An extension of the Scharfetter-Gummel scheme guaranteeing consistency with thermodynamic equilibrium is studied. It is derived by replacing the thermal voltage with an averaged diffusion enhancement for which we provide a new explicit formula. This approach avoids solving the costly local nonlinear equations defining the current for generalized Scharfetter-Gummel schemes. -
M. Liero, Th. Koprucki, A. Fischer, R. Scholz, A. Glitzky, p-Laplace thermistor modeling of electrothermal feedback in organic semiconductors, ZAMP Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 66 (2015), pp. 2957--2977.
Abstract
In large-area Organic Light-Emitting Diodes (OLEDs) spatially inhomogeneous luminance at high power due to inhomogeneous current flow and electrothermal feedback can be observed. To describe these self-heating effects in organic semiconductors we present a stationary thermistor model based on the heat equation for the temperature coupled to a p-Laplace-type equation for the electrostatic potential with mixed boundary conditions. The p-Laplacian describes the non-Ohmic electrical behavior of the organic material. Moreover, an Arrhenius-like temperature dependency of the electrical conductivity is considered. We introduce a finite-volume scheme for the system and discuss its relation to recent network models for OLEDs. In two spatial dimensions we derive a priori estimates for the temperature and the electrostatic potential and prove the existence of a weak solution by Schauder's fixed point theorem. -
D. Peschka, M. Thomas, A. Glitzky, R. Nürnberg, K. Gärtner, M. Virgilio, S. Guha, G. Capellini, Th. Koprucki, Th. Schröder, Modeling of edge-emitting lasers based on tensile strained germanium microstrips, IEEE Photonics Journal, 7 (2015), pp. 1502115/1--1502115/15, DOI 10.1109/JPHOT.2015.2427093 .
Abstract
In this paper we present a thorough modeling of an edge-emitting laser based on strained germanium microstrips. The full band structure of the tensile strained germanium (Ge) layer enters the calculation of optical properties. Material gain for strained Ge is used in the two-dimensional simulation of the carrier transport and of the optical field within a cross section of the microstrips orthogonal to the optical cavity. We study optoelectronic properties of the device for two different designs. The simulation results are very promising as they show feasible ways towards Ge emitter devices with lower threshold currents and higher efficiency as published insofar. -
G. Ali, A. Bartel, N. Rotundo, Index-2 elliptic partial differential-algebraic models for circuits and devices, Journal of Mathematical Analysis and Applications, 423 (2015), pp. 1348--1369.
-
C. Kreisbeck, L. Mascarenhas, Asymptotic spectral analysis in semiconductor nanowire heterostructures, Applicable Analysis. An International Journal, (published online on June 2, 2014), DOI 10.1080/00036811.2014.919052 .
-
P. Exner, H. Neidhardt, M. Tatar, V. Zagrebnov, Non-equilibrium current via geometric scatterers, Journal of Physics. A. Mathematical and General, 47 (2014), pp. 395301/1--395301/16.
-
A. Fischer, Th. Koprucki, K. Gärtner, M.L. Tietze, J. Brückner, B. Lüssem, K. Leo, A. Glitzky, R. Scholz, Feel the heat: Nonlinear electrothermal feedback in Organic LEDs, Advanced Functional Materials, 24 (2014), pp. 3367--3374.
Abstract
For lighting applications, Organic light-emitting diodes (OLED) need much higher brightness than for displays, leading to self-heating. Due to the temperature-activated transport in organic semiconductors, this can result in brightness inhomogeneities and catastrophic failure. Here, we show that due to the strong electrothermal feedback of OLEDs, the common spatial current and voltage distribution is completely changed, requiring advanced device modeling and operation concepts. Our study clearly demonstrates the effect of negative differential resistance (NDR) in OLEDs induced by self-heating. As a consequence, for increasing voltage, regions with declining voltages are propagating through the device, and even more interestingly, a part of these regions show even decreasing currents, leading to strong local variation in luminance. The expected breakthrough of OLED lighting technology will require an improved price performance ratio, and the realization of modules with very high brightness but untainted appearance is considered to be an essential step into this direction. Thus, a deeper understanding of the control of electrothermal feedback will help to make OLEDs in lighting more competitive. -
TH. Koprucki, K. Gärtner, Discretization scheme for drift-diffusion equations with strong diffusion enhancement, Optical and Quantum Electronics, 45 (2013), pp. 791--796.
Abstract
Inspired by organic semiconductor models based on hopping transport introducing Gauss-Fermi integrals a nonlinear generalization of the classical Scharfetter-Gummel scheme is derived for the distribution function F(η)=1/(exp(-η)+γ). This function provides an approximation of the Fermi-Dirac integrals of different order and restricted argument ranges. The scheme requires the solution of a nonlinear equation per edge and continuity equation to calculate the edge currents. In the current formula the density-dependent diffusion enhancement factor, resulting from the generalized Einstein relation, shows up as a weighting factor. Additionally the current modifies the argument of the Bernoulli functions. -
M. Liero, A. Mielke, Gradient structures and geodesic convexity for reaction-diffusion systems, Philosophical Transactions of the Royal Society A : Mathematical, Physical & Engineering Sciences, 371 (2013), pp. 20120346/1--20120346/28.
Abstract
We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory. We consider systems of reaction-diffusion equations as gradient systems with respect to an entropy functional and a dissipation metric given in terms of a so-called Onsager operator, which is a sum of a diffusion part of Wasserstein type and a reaction part. We provide methods for establishing geodesic lambda-convexity of the entropy functional by purely differential methods, thus circumventing arguments from mass transportation. Finally, several examples, including a drift-diffusion system, provide a survey on the applicability of the theory. -
A. Fischer, P. Pahner, B. Lüssem, K. Leo, R. Scholz, Th. Koprucki, K. Gärtner, A. Glitzky, Self-heating, bistability, and thermal switching in organic semiconductors, Physical Review Letters, 110 (2013), pp. 126601/1--126601/5.
Abstract
We demonstrate electric bistability induced by the positive feedback of self-heating onto the thermally activated conductivity in a two-terminal device based on the organic semiconductor C60. The central undoped layer with a thickness of 200 nm is embedded between thinner n-doped layers adjacent to the contacts minimizing injection barriers. The observed current-voltage characteristics follow the general theory for thermistors described by an Arrhenius-like conductivity law. Our findings including hysteresis phenomena are of general relevance for the entire material class since most organic semiconductors can be described by a thermally activated conductivity. -
A. Glitzky, A. Mielke, A gradient structure for systems coupling reaction-diffusion effects in bulk and interfaces, ZAMP Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 64 (2013), pp. 29--52.
Abstract
We derive gradient-flow formulations for systems describing drift-diffusion processes of a finite number of species which undergo mass-action type reversible reactions. Our investigations cover heterostructures, where material parameter may depend in a nonsmooth way on the space variable. The main results concern a gradient flow formulation for electro-reaction-diffusion systems with active interfaces permitting drift-diffusion processes and reactions of species living on the interface and transfer mechanisms allowing bulk species to jump into an interface or to pass through interfaces. The gradient flows are formulated in terms of two functionals: the free energy and the dissipation potential. Both functionals consist of a bulk and an interface integral. The interface integrals determine the interface dynamics as well as the self-consistent coupling to the model in the bulk. The advantage of the gradient structure is that it automatically generates thermodynamically consistent models. -
P.N. Racec, S. Schade, H.-Chr. Kaiser, Eigensolutions of the Wigner--Eisenbud problem for a cylindrical nanowire within finite volume method, Journal of Computational Physics, 252 (2013), pp. 52--64.
Abstract
We present a finite volume method for computing a representative range of eigenvalues and eigenvectors of the Schrödinger operator on a three dimensional cylindrically symmetric bounded domain with mixed boundary conditions. More specifically, we deal with a semiconductor nanowire which consists of a dominant host material and contains heterostructure features such as double-barriers or quantum dots. The three dimensional Schrödinger operator is reduced to a family of two dimensional Schrödinger operators distinguished by a centrifugal potential. Ultimately, we numerically treat them by means of a finite volume method. We consider a uniform, boundary conforming Delaunay mesh, which additionally conforms to the material interfaces. The 1/r singularity is eliminated by approximating r at the vertexes of the Voronoi boxes. We study how the anisotropy of the effective mass tensor acts on the uniform approximation of the first K eigenvalues and eigenvectors and their sequential arrangement. There exists an optimal uniform Delaunay discretization with matching anisotropy. This anisotropic discretization yields best accuracy also in the presence of a mildly varying scattering potential, shown exemplarily for a nanowire resonant tunneling diode. For potentials with 1/r singularity one retrieves the theoretically established first order convergence, while the second order convergence is recovered only on uniform grids with an anisotropy correction. -
A. Fischer, P. Pahner, B. Lüssem, K. Leo, R. Scholz, Th. Koprucki, J. Fuhrmann, K. Gärtner, A. Glitzky, Self-heating effects in organic semiconductor crossbar structures with small active area, Organic Electronics, 13 (2012), pp. 2461--2468.
Abstract
We studied the influence of heating effects in an organic device containing a layer sequence of n-doped / intrinsic / n-doped C60 between crossbar metal electrodes. A strong positive feedback between current and temperature occurs at high current densities beyond 100 A/cm2, as predicted by the extended Gaussian disorder model (EGDM) applicable to organic semiconductors. These devices give a perfect setting for studying the heat transport at high power densities because C60 can withstand temperatures above 200° C. Infrared images of the device and detailed numerical simulations of the heat transport demonstrate that the electrical circuit produces a superposition of a homogeneous power dissipation in the active volume and strong heat sources localized at the contact edges. Hence, close to the contact edges, the current density is significantly enhanced with respect to the central region of the device, demonstrating that three-dimensional effects have a strong impact on a device with seemingly one-dimensional transport. -
A. Glitzky, An electronic model for solar cells including active interfaces and energy resolved defect densities, SIAM Journal on Mathematical Analysis, 44 (2012), pp. 3874--3900.
Abstract
We introduce an electronic model for solar cells taking into account heterostructures with active interfaces and energy resolved volume and interface trap densities. The model consists of continuity equations for electrons and holes with thermionic emission transfer conditions at the interface and of ODEs for the trap densities with energy level and spatial position as parameters, where the right hand sides contain generation-recombination as well as ionization reactions. This system is coupled with a Poisson equation for the electrostatic potential. We show the thermodynamic correctness of the model and prove a priori estimates for the solutions to the evolution system. Moreover, existence and uniqueness of weak solutions of the problem are proven. For this purpose we solve a regularized problem and verify bounds of the corresponding solution not depending on the regularization level. -
TH. Koprucki, A. Wilms, A. Knorr, U. Bandelow, Modeling of quantum dot lasers with microscopic treatment of Coulomb effects, Optical and Quantum Electronics, 42 (2011), pp. 777--783.
Abstract
We present a spatially resolved semiclassical model for the simulation of semiconductor quantum-dot lasers including a multi-species description for the carriers along the optical active region. The model links microscopic determined quantities like scattering rates and dephasing times, that essentially depend via Coulomb interaction on the carrier densities, with macroscopic transport equations and equations for the optical field. -
A. Glitzky, Analysis of electronic models for solar cells including energy resolved defect densities, Mathematical Methods in the Applied Sciences, 34 (2011), pp. 1980--1998.
Abstract
We introduce an electronic model for solar cells including energy resolved defect densities. The resulting drift-diffusion model corresponds to a generalized van Roosbroeck system with additional source terms coupled with ODEs containing space and energy as parameters for all defect densities. The system has to be considered in heterostructures and with mixed boundary conditions from device simulation. We give a weak formulation of the problem. If the boundary data and the sources are compatible with thermodynamic equilibrium the free energy along solutions decays monotonously. In other cases it may be increasing, but we estimate its growth. We establish boundedness and uniqueness results and prove the existence of a weak solution. This is done by considering a regularized problem, showing its solvability and the boundedness of its solutions independent of the regularization level. -
J.A. Griepentrog, L. Recke, Local existence, uniqueness, and smooth dependence for nonsmooth quasilinear parabolic problems, Journal of Evolution Equations, 10 (2010), pp. 341--375.
Abstract
A general theory on local existence, uniqueness, regularity, and smooth dependence in Hölder spaces for a general class of quasilinear parabolic initial boundary value problems with nonsmooth data has been developed. As a result the gap between low smoothness of the data, which is typical for many applications, and high smoothness of the solutions, which is necessary for the applicability of differential calculus to the abstract formulations of the initial boundary value problems, has been closed. The main tools are new maximal regularity results of the first author in Sobolev-Morrey spaces, linearization techniques and the Implicit Function Theorem. Typical applications are transport processes of charged particles in semiconductor heterostructures, phase separation processes of nonlocally interacting particles, chemotactic aggregation in heterogeneous environments as well as optimal control by means of quasilinear elliptic and parabolic PDEs with nonsmooth data. -
M.-R. Dachner, E. Malic, M. Richter, A. Carmele, J. Kabuss, A. Wilms, J.-E. Kim, G. Hartmann, J. Wolters, U. Bandelow, A. Knorr, Theory of carrier and photon dynamics in quantum dot light emitters, physica status solidi (b), 247 (2010), pp. 809--828.
Abstract
We present a microscopic theory describing the charge carrier and light emission dynamics in quantum dot (QD) light emitters. The theory covers non-classical light emission (fluorescence and Raman emission) in the low carrier injection limit as well as laser emission and pulse amplification in the high carrier injection limit. The theoretical approach is based on QD Bloch equations including microscopically calculated Coulomb and electron-phonon scattering rates between bound QD, continuous wetting layer (WL) and bulk states. In the low carrier density limit, multi-phonon relaxation is the dominant process, while at high charge carrier densities, Coulomb scattering dominates the dynamics. Using an equation of motion approach, we address (i) time-resolved fluorescence and Raman emission, (ii) electrical injection and charge carrier transfer from bulk into WL and QD states, (iii) single photon emission and (iv) gain dynamics of QD amplifiers and lasing dynamics in QD vertical-cavity surface-emitting lasers (VCSELs) at high injection currents. -
A. Glitzky, J.A. Griepentrog, Discrete Sobolev--Poincaré inequalities for Voronoi finite volume approximations, SIAM Journal on Numerical Analysis, 48 (2010), pp. 372--391.
Abstract
We prove a discrete Sobolev-Poincare inequality for functions with arbitrary boundary values on Voronoi finite volume meshes. We use Sobolev's integral representation and estimate weakly singular integrals in the context of finite volumes. We establish the result for star shaped polyhedral domains and generalize it to the finite union of overlapping star shaped domains. In the appendix we prove a discrete Poincare inequality for space dimensions greater or equal to two. -
A. Glitzky, K. Gärtner, Existence of bounded steady state solutions to spin-polarized drift-diffusion systems, SIAM Journal on Mathematical Analysis, 41 (2010), pp. 2489--2513.
Abstract
We study a stationary spin-polarized drift-diffusion model for semiconductor spintronic devices. This coupled system of continuity equations and a Poisson equation with mixed boundary conditions in all equations has to be considered in heterostructures. In 3D we prove the existence and boundedness of steady states. If the Dirichlet conditions are compatible or nearly compatible with thermodynamic equilibrium the solution is unique. The same properties are obtained for a space discretized version of the problem: Using a Scharfetter-Gummel scheme on 3D boundary conforming Delaunay grids we show existence, boundedness and, for small applied voltages, the uniqueness of the discrete solution. -
K. Hoke, H.-Chr. Kaiser, J. Rehberg, Analyticity for some operator functions from statistical quantum mechanics, Annales Henri Poincare. A Journal of Theoretical and Mathematical Physics, 10 (2009), pp. 749--771.
Abstract
For rather general thermodynamic equilibrium distribution functions the density of a statistical ensemble of quantum mechanical particles depends analytically on the potential in the Schrödinger operator describing the quantum system. A key to the proof is that the resolvent to a power less than one of an elliptic operator with non-smooth coefficients, and mixed Dirichlet/Neumann boundary conditions on a bounded up to three-dimensional Lipschitz domain factorizes over the space of essentially bounded functions. -
P.N. Racec, R. Racec, H. Neidhardt, Evanescent channels and scattering in cylindrical nanowire heterostructures, Phys. Rev. B., 79 (2009), pp. 155305/1--155305/14.
Abstract
We investigate the scattering phenomena produced by a general finite range non-separable potential in a multi-channel two-probe cylindrical nanowire heterostructure. The multi-channel current scattering matrix is efficiently computed using the R-matrix formalism extended for cylindrical coordinates. Considering the contribution of the evanescent channels to the scattering matrix, we are able to put in evidence the specific dips in the tunneling coefficient in the case of an attractive potential. The cylindrical symmetry cancels the ”selection rules” known for Cartesian coordinates. If the attractive potential is superposed over a non-uniform potential along the nanowire, then resonant transmission peaks appear. We can characterize them quantitatively through the poles of the current scattering matrix. Detailed maps of the localization probability density sustain the physical interpretation of the resonances (dips and peaks). Our formalism is applied to a variety of model systems like a quantum dot, a core/shell quantum ring or a double barrier, embedded into the nano-cylinder. -
R. Haller-Dintelmann, Ch. Meyer, J. Rehberg, A. Schiela, Hölder continuity and optimal control for nonsmooth elliptic problems, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, 60 (2009), pp. 397--428.
Abstract
The well known De Giorgi result on Hölder continuity for solutions of the Dirichlet problem is re-established for mixed boundary value problems, provided that the underlying domain is a Lipschitz domain and the border between the Dirichlet and the Neumann boundary part satisfies a very general geometric condition. Implications of this result for optimal control theory are presented. -
R. Haller-Dintelmann, J. Rehberg, Maximal parabolic regularity for divergence operators including mixed boundary conditions, Journal of Differential Equations, 247 (2009), pp. 1354--1396.
Abstract
We show that elliptic second order operators $A$ of divergence type fulfill maximal parabolic regularity on distribution spaces, even if the underlying domain is highly non-smooth and $A$ is complemented with mixed boundary conditions. Applications to quasilinear parabolic equations with non-smooth data are presented. -
K. Gärtner, Existence of bounded discrete steady state solutions of the van Roosbroeck system on boundary conforming Delaunay grids, SIAM Journal on Scientific Computing, 31 (2009), pp. 1347--1362.
Abstract
The classic van Roosbroeck system describes the carrier transport in semiconductors in a drift diffusion approximation. Its analytic steady state solutions fulfill bounds for some mobility and recombination/generation models. The main goal of this paper is to establish the identical bounds for discrete in space, steady state solutions on 3d boundary conforming Delaunay grids and the classical Scharfetter-Gummel-scheme. Together with a uniqueness proof for small applied voltages and the known dissipativity (continuous as well as space and time discrete) these discretization techniques carry over the essential analytic properties to the discrete case. The proofs are of interest for deriving averaging schemes for space or state dependent material parameters, which are preserving these qualitative properties, too. To illustrate the properties of the scheme 1, 4, 16 elementary cells of a modified CoolMOS like structure are depleted by increasing the applied voltage until steady state avalanche breakdown occurs. -
A. Glitzky, Energy estimates for electro-reaction-diffusion systems with partly fast kinetics, Discrete and Continuous Dynamical Systems, 25 (2009), pp. 159--174.
Abstract
We start from a basic model for the transport of charged species in heterostructures containing the mechanisms diffusion, drift and reactions in the domain and at its boundary. Considering limit cases of partly fast kinetics we derive reduced models. This reduction can be interpreted as some kind of projection scheme for the weak formulation of the basic electro--reaction--diffusion system. We verify assertions concerning invariants and steady states and prove the monotone and exponential decay of the free energy along solutions to the reduced problem and to its fully implicit discrete-time version by means of the results of the basic problem. Moreover we make a comparison of prolongated quantities with the solutions to the basic model. -
A. Glitzky, K. Gärtner, Energy estimates for continuous and discretized electro-reaction-diffusion systems, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 70 (2009), pp. 788--805.
Abstract
We consider electro-reaction-diffusion systems consisting of continuity equations for a finite number of species coupled with a Poisson equation. We take into account heterostructures, anisotropic materials and rather general statistic relations.
We investigate thermodynamic equilibria and prove for solutions to the evolution system the monotone and exponential decay of the free energy to its equilibrium value. Here the essential idea is an estimate of the free energy by the dissipation rate which is proved indirectly.
The same properties are shown for an implicit time discretized version of the problem. Moreover, we provide a space discretized scheme for the electro-reaction-diffusion system which is dissipative (the free energy decays monotonously). On a fixed grid we use for each species different Voronoi boxes which are defined with respect to the anisotropy matrix occurring in the flux term of this species. -
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Classical solutions of drift-diffusion equations for semiconductor devices: The 2D case, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 71 (2009), pp. 1584--1605.
Abstract
We regard drift-diffusion equations for semiconductor devices in Lebesgue spaces. To that end we reformulate the (generalized) van Roosbroeck system as an evolution equation for the potentials to the driving forces of the currents of electrons and holes. This evolution equation falls into a class of quasi-linear parabolic systems which allow unique, local in time solution in certain Lebesgue spaces. In particular, it turns out that the divergence of the electron and hole current is an integrable function. Hence, Gauss' theorem applies, and gives the foundation for space discretization of the equations by means of finite volume schemes. Moreover, the strong differentiability of the electron and hole density in time is constitutive for the implicit time discretization scheme. Finite volume discretization of space, and implicit time discretization are accepted custom in engineering and scientific computing. ---This investigation puts special emphasis on non-smooth spatial domains, mixed boundary conditions, and heterogeneous material compositions, as required in electronic device simulation. -
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Monotonicity properties of the quantum mechanical particle density: An elementary proof, Monatshefte fur Mathematik, 158 (2009), pp. 179--185.
Abstract
An elementary proof of the anti-monotonicity of the quantum mechanical particle density with respect to the potential in the Hamiltonian is given for a large class of admissible thermodynamic equilibrium distribution functions. In particular the zero temperature case is included. -
H. Cornean, K. Hoke, H. Neidhardt, P.N. Racec, J. Rehberg, A Kohn--Sham system at zero temperature, Journal of Physics. A. Mathematical and General, 41 (2008), pp. 385304/1--385304/21.
Abstract
An one-dimensional Kohn-Sham system for spin particles is considered which effectively describes semiconductor nanostructures and which is investigated at zero temperature. We prove the existence of solutions and derive a priori estimates. For this purpose we find estimates for eigenvalues of the Schrödinger operator with effective Kohn-Sham potential and obtain $W^1,2$-bounds of the associated particle density operator. Afterwards, compactness and continuity results allow to apply Schauder's fixed point theorem. In case of vanishing exchange-correlation potential uniqueness is shown by monotonicity arguments. Finally, we investigate the behavior of the system if the temperature approaches zero. -
R. Haller-Dintelmann, H.-Chr. Kaiser, J. Rehberg, Elliptic model problems including mixed boundary conditions and material heterogeneities, Journal de Mathématiques Pures et Appliquées, 89 (2008), pp. 25--48.
-
M. Hieber, J. Rehberg, Quasilinear parabolic systems with mixed boundary conditions on nonsmooth domains, SIAM Journal on Mathematical Analysis, 40 (2008), pp. 292--305.
Abstract
In this paper we investigate quasilinear systems of reaction-diffusion equations with mixed Dirichlet-Neumann bondary conditions on non smooth domains. Using techniques from maximal regularity and heat-kernel estimates we prove existence of a unique solution to systems of this type. -
A. Glitzky, R. Hünlich, Stationary solutions to an energy model for semiconductor devices where the equations are defined on different domains, Mathematische Nachrichten, 281 (2008), pp. 1676--1693.
Abstract
We discuss a stationary energy model from semiconductor modelling. We accept the more realistic assumption that the continuity equations for electrons and holes have to be considered only in a subdomain $Omega_0$ of the domain of definition $Omega$ of the energy balance equation and of the Poisson equation. Here $Omega_0$ corresponds to the region of semiconducting material, $OmegasetminusOmega_0$ represents passive layers. Metals serving as contacts are modelled by Dirichlet boundary conditions. We prove a local existence and uniqueness result for the two-dimensional stationary energy model. For this purpose we derive a $W^1,p$-regularity result for solutions of systems of elliptic equations with different regions of definition and use the Implicit Function Theorem. -
A. Glitzky, Analysis of a spin-polarized drift-diffusion model, Advances in Mathematical Sciences and Applications, 18 (2008), pp. 401--427.
Abstract
We introduce a spin-polarized drift-diffusion model for semiconductor spintronic devices. This coupled system of continuity equations and a Poisson equation with mixed boundary conditions in all equations has to be considered in heterostructures. We give a weak formulation of this problem and prove an existence and uniqueness result for the instationary problem. If the boundary data is compatible with thermodynamic equilibrium the free energy along the solution decays monotonously and exponentially to its equilibrium value. In other cases it may be increasing but we estimate its growth. Moreover we give upper and lower estimates for the solution. -
A. Glitzky, Exponential decay of the free energy for discretized electro-reaction-diffusion systems, Nonlinearity, 21 (2008), pp. 1989--2009.
Abstract
Our focus are electro-reaction-diffusion systems consisting of continuity equations for a finite number of species coupled with a Poisson equation. We take into account heterostructures, anisotropic materials and rather general statistical relations. We introduce a discretization scheme (in space and fully implicit in time) using a fixed grid but for each species different Voronoi boxes which are defined with respect to the anisotropy matrix occurring in the flux term of this species. This scheme has the special property that it preserves the main features of the continuous systems, namely positivity, dissipativity and flux conservation. For the discretized electro-reaction-diffusion system we investigate thermodynamic equilibria and prove for solutions to the evolution system the monotone and exponential decay of the free energy to its equilibrium value. The essential idea is an estimate of the free energy by the dissipation rate which is proved indirectly. -
J.A. Griepentrog, Maximal regularity for nonsmooth parabolic problems in Sobolev--Morrey spaces, Advances in Differential Equations, 12 (2007), pp. 1031--1078.
Abstract
This text is devoted to maximal regularity results for second order parabolic systems on LIPSCHITZ domains of space dimension greater or equal than three with diagonal principal part, nonsmooth coefficients, and nonhomogeneous mixed boundary conditions. We show that the corresponding class of initial boundary value problems generates isomorphisms between two scales of SOBOLEV-MORREY spaces for solutions and right hand sides introduced in the first part of our presentation. The solutions depend smoothly on the data of the problem. Moreover, they are HOELDER continuous in time and space up to the boundary for a certain range of MORREY exponents. Due to the complete continuity of embedding and trace maps these results remain true for a broad class of unbounded lower order coefficients. -
J.A. Griepentrog, Sobolev--Morrey spaces associated with evolution equations, Advances in Differential Equations, 12 (2007), pp. 781--840.
Abstract
In this text we introduce new classes of SOBOLEV-MORREY spaces being adequate for the regularity theory of second order parabolic boundary value problems on LIPSCHITZ domains of space dimension greater or equal than three with nonsmooth coefficients and mixed boundary conditions. We prove embedding and trace theorems as well as invariance properties of these spaces with respect to localization, LIPSCHITZ transformation, and reflection. In the second part of our presentation we show that the class of second order parabolic systems with diagonal principal part generates isomorphisms between the above mentioned SOBOLEV-MORREY spaces of solutions and right hand sides. -
M. Radziunas, A. Glitzky, U. Bandelow, M. Wolfrum, U. Troppenz, J. Kreissl, W. Rehbein, Improving the modulation bandwidth in semiconductor lasers by passive feedback, IEEE J. Select. Topics Quantum Electron., 13 (2007), pp. 136--142.
-
J. Even, F. Doré, C. Cornet, L. Pedesseau, A. Schliwa, D. Bimberg, Semianalytical evaluation of linear and nonlinear piezoelectric potentials for quantum nanostructures with axial symmetry, Applied Physics Letters, 91 (2007), pp. 122112/1--122112/3.
-
A. Marent, M. Geller, A. Schliwa, D. Feise, K. Pötschke, D. Bimberg, N. Akcay, N. Öncan, 10$^6$ years extrapolated hole storage time in GaSb/AlAs quantum dots, Applied Physics Letters, 91 (2007), pp. 242109/1--242109/3.
-
V. Mlinar, A. Schliwa, D. Bimberg, F.M. Peeters, Theoretical study of electronic and optical properties of inverted GaAs/AlGaAs quantum dots with smoothed interfaces in an external magnetic field, Phys. Rev. B., 75 (2007), pp. 205308/1--205308/9.
-
M. Winkelnkemper, R. Seguin, S. Rodt, A. Schliwa, L. Reimann, A. Strittmatter, A. Hoffmann, D. Bimberg, Polarized emission lines from A- and B-type excitonic complexes in single InGaN/GaN quantum dots, Journal of Applied Physics, 101 (2007), pp. 113708/1--113708/4.
-
U. Wulf, P.N. Racec, E.R. Racec, Admittance of planar two-terminal quantum systems, Phys. Rev. B., 75 (2007), pp. 075320/1--075320/9.
-
J. Elschner, H.-Chr. Kaiser, J. Rehberg, G. Schmidt, $W^1,q$ regularity results for elliptic transmission problems on heterogeneous polyhedra, Mathematical Models & Methods in Applied Sciences, 17 (2007), pp. 593--615.
-
J. Elschner, J. Rehberg, G. Schmidt, Optimal regularity for elliptic transmission problems including $C^1$ interfaces, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 9 (2007), pp. 233--252.
Abstract
We prove an optimal regularity result for elliptic operators $-nabla cdot mu nabla:W^1,q_0 rightarrow W^-1,q$ for a $q>3$ in the case when the coefficient function $mu$ has a jump across a $C^1$ interface and is continuous elsewhere. A counterexample shows that the $C^1$ condition cannot be relaxed in general. Finally, we draw some conclusions for corresponding parabolic operators. -
A. Glitzky, R. Hünlich, Resolvent estimates in $W^-1,p$ related to strongly coupled linear parabolic systems with coupled nonsmooth capacities, Mathematical Methods in the Applied Sciences, 30 (2007), pp. 2215--2232.
Abstract
We investigate linear parabolic systems with coupled nonsmooth capacities and mixed boundary conditions. We prove generalized resolvent estimates in $W^-1,p$ spaces. The method is an appropriate modification of a technique introduced by Agmon to obtain $L^p$ estimates for resolvents of elliptic differential operators in the case of smooth boundary conditions. Moreover, we establish an existence and uniqueness result. -
H. Neidhardt, J. Rehberg, Scattering matrix, phase shift, spectral shift and trace formula for one-dimensional Schrödinger-type operators, Integral Equations and Operator Theory, 58 (2007), pp. 407--431.
Abstract
The paper is devoted to Schroedinger operators on bounded intervals of the real axis with dissipative boundary conditions. In the framework of the Lax-Phillips scattering theory the asymptotic behaviour of the phase shift is investigated in detail and its relation to the spectral shift is discussed, in particular, trace formula and Birman-Krein formula are verified directly. The results are used for dissipative Schroedinger-Poisson systems. -
P.N. Racec, U. Wulf, Small-signal circuit elements of MIS-type nanostructures, Solid State Phenomena, 121--123 (2007), pp. 549--552.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Classical solutions of quasilinear parabolic systems on two dimensional domains, NoDEA. Nonlinear Differential Equations and Applications, 13 (2006), pp. 287-310.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Convexity of trace functionals and Schrödinger operators, Journal of Functional Analysis, 234 (2006), pp. 45--69.
-
M. Baro, N. Ben Abdallah, P. Degond, A. El Ayyadi, A 1D coupled Schrödinger drift-diffusion model including collisions, Journal of Computational Physics, 203 (2005), pp. 129-153.
-
M. Baro, H. Neidhardt, J. Rehberg, Current coupling of drift-diffusion models and dissipative Schrödinger--Poisson systems: Dissipative hybrid models, SIAM Journal on Mathematical Analysis, 37 (2005), pp. 941--981.
-
M. Baro, M. Demuth, E. Giere, Stable continuous spectra for differential operators of arbitrary order, Analysis and Applications, 3 (2005), pp. 223-250.
-
TH. Koprucki, M. Baro, U. Bandelow, Th. Tien, F. Weik, J.W. Tomm, M. Grau, M.-Ch. Amann, Electronic structure and optoelectronic properties of strained InAsSb/GaSb multiple quantum wells, Applied Physics Letters, 87 (2005), pp. 181911/1--181911/3.
-
H. Neidhardt, J. Rehberg, Uniqueness for dissipative Schrödinger--Poisson systems, Journal of Mathematical Physics, 46 (2005), pp. 113513/1--113513/28.
-
A. Glitzky, R. Hünlich, Global existence result for pair diffusion models, SIAM Journal on Mathematical Analysis, 36 (2005), pp. 1200--1225.
-
A. Glitzky, R. Hünlich, Stationary energy models for semiconductor devices with incompletely ionized impurities, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 85 (2005), pp. 778--792.
-
J. Rehberg, Quasilinear parabolic equations in $L^p$, Progress in Nonlinear Differential Equations and their Applications, 64 (2005), pp. 413-419.
-
M. Baro, H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, A quantum transmitting Schrödinger-Poisson system, Reviews in Mathematical Physics. A Journal for Both Review and Original Research Papers in the Field of Mathematical Physics, 16 (2004), pp. 281--330.
-
M. Baro, H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Dissipative Schrödinger--Poisson systems, Journal of Mathematical Physics, 45 (2004), pp. 21--43.
-
V. Maz'ya, J. Elschner, J. Rehberg, G. Schmidt, Solutions for quasilinear nonsmooth evolution systems in $L^p$, Archive for Rational Mechanics and Analysis, 171 (2004), pp. 219--262.
-
A. Glitzky, W. Merz, Single dopant diffusion in semiconductor technology, Mathematical Methods in the Applied Sciences, 27 (2004), pp. 133--154.
-
A. Glitzky, R. Hünlich, Stationary solutions of two-dimensional heterogeneous energy models with multiple species, Banach Center Publications, 66 (2004), pp. 135-151.
-
A. Glitzky, Electro-reaction-diffusion systems with nonlocal constraints, Mathematische Nachrichten, 277 (2004), pp. 14--46.
-
M. Baro, H. Neidhardt, Dissipative Schrödinger-type operator as a model for generation and recombination, Journal of Mathematical Physics, 44 (2003), pp. 2373--2401.
-
H. Gajewski, I.V. Skrypnik, On the uniqueness of solutions for nonlinear elliptic-parabolic equations, Journal of Evolution Equations, 3 (2003), pp. 247--281.
-
H. Gajewski, I.V. Skrypnik, To the uniqueness problem for nonlinear elliptic equations, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 52 (2003), pp. 291--304.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Macroscopic current induced boundary conditions for Schrödinger-type operators, Integral Equations and Operator Theory, 45 (2003), pp. 39--63.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, On 1-dimensional dissipative Schrödinger-type operators, their dilations and eigenfunction expansions, Mathematische Nachrichten, 252 (2003), pp. 51--69.
-
G. Albinus, H. Gajewski, R. Hünlich, Thermodynamic design of energy models of semiconductor devices, Nonlinearity, 15 (2002), pp. 367--383.
-
J.A. Griepentrog, K. Gröger, H.-Chr. Kaiser, J. Rehberg, Interpolation for function spaces related to mixed boundary value problems, Mathematische Nachrichten, 241 (2002), pp. 110--120.
-
J.A. Griepentrog, Linear elliptic boundary value problems with non-smooth data: Campanato spaces of functionals, Mathematische Nachrichten, 243 (2002), pp. 19--42.
-
H.-Chr. Kaiser, H. Neidhardt, J. Rehberg, Density and current of a dissipative Schrödinger operator, Journal of Mathematical Physics, 43 (2002), pp. 5325--5350.
-
A. Glitzky, R. Hünlich, Global properties of pair diffusion models, Advances in Mathematical Sciences and Applications, 11 (2001), pp. 293--321.
-
J.A. Griepentrog, H.-Chr. Kaiser, J. Rehberg, Heat kernel and resolvent properties for second order elliptic differential operators with general boundary conditions on $Lsp p$, Advances in Mathematical Sciences and Applications, 11 (2001), pp. 87--112.
-
W. Merz, A. Glitzky, R. Hünlich, K. Pulverer, Strong solutions for pair diffusion models in homogeneous semiconductors, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 2 (2001), pp. 541-567.
-
I.V. Skrypnik, H. Gajewski, On the uniqueness of solution to nonlinear elliptic problem (in Ukrainian), Dopovidi Natsionalnoi Akademii Nauk Ukraini. Matematika. Prirodoznavstvo. Tekhnichni Nauki, (2001), pp. 28--32.
-
J.A. Griepentrog, L. Recke, Linear elliptic boundary value problems with non-smooth data: Normal solvability on Sobolev-Campanato spaces, Mathematische Nachrichten, 225 (2001), pp. 39--74.
-
U. Bandelow, H.-Chr. Kaiser, Th. Koprucki, J. Rehberg, Spectral properties of $k cdot p$ Schrödinger operators in one space dimension, Numerical Functional Analysis and Optimization. An International Journal, 21 (2000), pp. 379--409.
-
A. Glitzky, R. Hünlich, Electro-reaction-diffusion systems including cluster reactions of higher order, Mathematische Nachrichten, 216 (2000), pp. 95--118.
-
H.-Chr. Kaiser, J. Rehberg, About a stationary Schrödinger-Poisson system with Kohn-Sham potential in a bounded two- or three-dimensional domain, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 41 (2000), pp. 33--72.
-
J.A. Griepentrog, An application of the Implicit Function Theorem to an energy model of the semiconductor theory, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 79 (1999), pp. 43--51.
Abstract
In this paper we deal with a mathematical model for the description of heat conduction and carrier transport in semiconductor heterostructures. We solve a coupled system of nonlinear elliptic differential equations consisting of the heat equation with Joule heating as a source, the Poisson equation for the electric field an drift-diffusion equations with temperature dependent coefficients describing the charge and current conservation, subject to general thermal and electrical boundary conditions. We prove the existence and uniqueness of Holder continuous weak solutions near thermodynamic equilibria points using the Implicit Function Theorem. To show the differentiability of maps corresponding to the weak formulation of the problem we use regularity results from the theory of nonsmooth linear elliptic boundary value problems in Sobolev-Campanato spaces.
 Contributions to Collected Editions
Contributions to Collected Editions
-
R. Finn, M. O'Donovan, Th. Koprucki, S. Schulz, Theoretical investigation of optical polarisation in alloy disordered (Al,Ga)N quantum well systems, in: 25th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2025), IEEE, 2025, pp. 67--68, DOI 10.1109/NUSOD64393.2025.11199467 .
Abstract
Aluminium Gallium Nitride ((Al,Ga)N) is an ideal material for light emitting devices in the UV spectral range. However, these devices still suffer from low external quantum efficiencies, particularly in the deep-UV range. A contributor to the low external quantum efficiency is low light extraction efficiency (LEE), which is tightly linked to the valence band structure of (Al,Ga)N quantum wells. Theoretical studies that account for alloy disorder-induced valence band mixing effects in these structures are sparse. Here, we utilise an atomistic multiband tight-binding model to gain insight into the degree of optical polarisation in (Al,Ga)N quantum well systems. Special attention is paid to the impact of Al content, well width and carrier density in the wells. -
R. Finn, P. Farrell, T. Streckenbach, J. Moatti, S. Schulz, Th. Koprucki, M. O'Donovan, Multi-scale hybrid band simulation of (Al,Ga)N UV-C light emitting diodes, in: 25th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2025), IEEE, 2025, pp. 19--20, DOI 10.1109/NUSOD64393.2025.11199525 .
Abstract
Aluminium gallium nitride alloys are used for developing light emitting diodes operating in the UV part of the electromagnetic spectrum. These devices suffer from a low efficiency. To gain insight to this question we develop a 3-D modified drift-diffusion model which takes into account both alloy disorder effects and valence band mixing, and investigate the device efficiency. Results show that the current injection efficiency is strongly influenced by the chosen doping profile. -
A. Glitzky, On a drift-diffusion model for perovskite solar cells, in: 94th Annual Meeting 2024 of the International Association of Applied Mathematics and Mechanics (GAMM), 24 of Proc. Appl. Math. Mech. (Special Issue), Wiley-VCH Verlag, Weinheim, 2024, pp. e202400017/1--e202400017/8, DOI 10.1002/pamm.202400017 .
Abstract
We introduce a vacancy-assisted charge transport model for perovskite solar cells. This instationary drift-diffusion system describes the motion of electrons, holes, and ionic vacancies and takes into account Fermi--Dirac statistics for electrons and holes and the Fermi--Dirac integral of order -1 for the mobile ionic vacancies in the perovskite. The free energy functional we work with corresponds to that choice of the statistical relations. To verify the existence of weak solutions, we consider a problem with regularized state equations and reaction terms on any arbitrarily chosen finite time interval. We motivate its solvability by time discretization and passage to the time-continuous limit. A priori estimates for the chemical potentials that are independent of the regularization level ensure the existence of solutions to the original problem. These types of estimates rely on Moser iteration techniques and can also be obtained for solutions to the original problem. -
A. Maltsi, A. Mielke, Th. Koprucki, Symmetries in Transmission Electron Microscopy images of semiconductor nanostructures with strain, in: 23nd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), P. Bardella, A. Tibaldi, eds., IEEE, 2023, pp. 111-112, DOI 10.1109/NUSOD59562.2023.10273568 .
Abstract
Transmission electron microscopy is often used to image semiconductor nanostructures with strain. The resulting images exhibit symmetries, the source of which is not always known. We prove mathematically that the intensities are invariant under specific transformations, which allows us to distinguish between symmetries of the imaging process itself and symmetries of the inclusion. -
M. O'Donovan, R. Finn, S. Schulz, Th. Koprucki, Atomistic study of Urbach tail energies in (Al,Ga)N quantum well systems, in: 23nd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), P. Bardella, A. Tibaldi, eds., IEEE, 2023, pp. 79--80, DOI 10.1109/NUSOD59562.2023.10273479 .
Abstract
Aluminium gallium nitride is a system of interest for developing ultraviolet (UV) optoelectronic devices. Here Urbach tails induced by carrier localization effects play a key role in determining device behaviour. We study the electronic structure of Al x Ga 1-x N/Al y Ga 1-y N single quantum wells using an atomistic framework. Results show that the density of states exhibits a tail at low energies due to disorder in the alloy microstructure. Our analysis allows for insight into the orbital character of the states forming the Urbach tails, which can affect light polarization characteristics, and important quantity for deep UV light emitters. -
R. Finn, M. O'Donovan, P. Farrell, T. Streckenbach, J. Moatti, Th. Koprucki, S. Schulz, Theoretical investigation of carrier transport and recombination processes for deep UV (Al,Ga)N light emitters, in: 23nd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), P. Bardella, A. Tibaldi, eds., IEEE, 2023, pp. 83--84, DOI 10.1109/NUSOD59562.2023.10273485 .
Abstract
We present a theoretical study on the impact of alloy disorder on carrier transport and recombination rates in an (Al,Ga)N single quantum well based LED operating in the deep UV spectral range. Our calculations indicate that alloy fluctuations enable percolative pathways which can result in improved carrier injection into the well, but may also increase carrier leakage from the well. Additionally, we find that alloy disorder induces carrier localization effects, a feature particularly noticeable for the holes. These localization effects can lead to locally increased carrier densities when compared to a virtual crystal approximation which neglects alloy disorder. We observe that both radiative and non-radiative recombination rates are increased. Our calculations also indicate that Auger--Meitner recombination increases faster than the radiative rate, based on a comparison with a virtual crystal approximation. -
A. Glitzky, M. Liero, A bulk-surface model for the electrothermal feedback in large-area organic light-emitting diodes, in: 93rd Annual Meeting 2023 of the International Association of Applied Mathematics and Mechanics (GAMM), 23 of Proc. Appl. Math. Mech. (Special Issue), Wiley-VCH Verlag, Weinheim, 2023, pp. e202300018/1--e202300018/8, DOI 10.1002/pamm.202300018 .
Abstract
This work deals with an effective bulk-surface thermistor model describing the electrothermal behavior of large-area thin-film organic light-emitting diodes (OLEDs). This model was rigorously derived from a -Laplace thermistor model by dimension reduction and consists of the heat equation in the three-dimensional glass substrate and two semi-linear equations describing the current flow through the electrodes coupled to algebraic equations that express the continuity of the electrical fluxes through the organic layers. The electrical problem lives on the surface of the glass substrate where the OLED is mounted. The source terms in the heat equation result from Joule heating and are concentrated on the part of the boundary where the current-flow problem is formulated. Schauder's fixed-point theorem is used to establish the existence of weak solutions to this effective system. Since the heat source terms at the surface are a priori only in L1, the concept of entropy solutions for the heat equation is worked with. -
D. Abdel, N. Courtier, P. Farrell, Volume exclusion effects in perovskite charge transport modeling, in: 2022 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2022), Turin, Italy, 2022, J. Piprek, P. Bardella, eds., IEEE, 2022, pp. 107--108, DOI 10.1109/NUSOD54938.2022.9894826 .
-
Y. Hadjimichael, O. Marquardt, Ch. Merdon, P. Farrell, Band structures in highly strained 3D nanowires, in: 2022 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2022), Turin, Italy, 2022, J. Piprek, Bardella Paolo, eds., IEEE, 2022, pp. 119--120, DOI 10.1109/NUSOD54938.2022.9894837 .
-
O. Marquardt, M. O'Donovan, S. Schulz, O. Brandt, Th. Koprucki, Influence of random alloy fluctuations on the electronic properties of axial (In,Ga)N/GaN nanowire heterostructures, in: 2022 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Turin, Italy, 2022, J. Piprek, P. Bardella, eds., IEEE, 2022, pp. 117--118, DOI 10.1109/NUSOD54938.2022.9894777 .
Abstract
Compound semiconductor heterostructures such as quantum dots, nanowires, or thin films, are commonly subject to randomly fluctuating alloy compositions if they contain ternary and quaternary alloys. These effects are obviously of an atomistic nature and thus rarely considered in heterostructure designs that require simulations on a continuum level for theory-guided design or interpretation of observations. In the following, we present a systematic approach to the treatment of alloy fluctuations in (In,Ga)N/GaN thin films and axial nanowire heterostructures. We demonstrate to what extent random alloy fluctuations can be treated in a continuum picture and discuss the impact of alloy fluctuations on the electronic properties of planar and nano wire-based (In,Ga)N/GaN heterostructures. -
S. Piani, W. Lei, L. Heltai, N. Rotundo, P. Farrell, Data-driven doping reconstruction, in: 2022 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2022), Turin, Italy, 2022, J. Piprek, P. Bardella, eds., IEEE, 2022, pp. 109--110, DOI 10.1109/NUSOD54938.2022.9894774 .
-
J. Moatti, P. Farrell, Comparison of flux discretizations for varying band-edge energies, in: 2022 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2022), Turin, Italy, 2022, J. Piprek, P. Bardella, eds., IEEE, 2022, pp. 103--104, DOI 10.1109/NUSOD54938.2022.9894742 .
-
M. O'Donovan, P. Farrell, T. Streckenbach, Th. Koprucki, S. Schulz, Carrier transport in (In,Ga)N quantum well systems: Connecting atomistic tight-binding electronic structure theory to drift-diffusion simulations, in: 2022 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Turin, Italy, 2022, J. Piprek, P. Bardella, eds., IEEE, 2022, pp. 97--98, DOI 10.1109/NUSOD54938.2022.9894745 .
-
D. Abdel, P. Farrell, J. Fuhrmann, Comparison of Scharfetter--Gummel schemes for (non-)degenerate semiconductor device simulation, in: Proceedings of the 20th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2020, J. Piprek, K. Hinzer, eds., IEEE Conference Publications Management Group, Piscataway, 2020, pp. 107--108.
-
S. Kayser, N. Rotundo, J. Fuhrmann, N. Dropka, P. Farrell, The lateral photovoltage scanning method (LPS): Understanding doping variations in silicon crystals, in: Proceedings of the 20th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2020, J. Piprek, K. Hinzer, eds., IEEE Conference Publications Management Group, Piscataway, 2020, pp. 49--50.
-
S. Schulz, D. Chaudhuri, M. O'Donovan, S. Patra, T. Streckenbach, P. Farrell, O. Marquardt, Th. Koprucki, Multi-scale modeling of electronic, optical, and transport properties of III-N alloys and heterostructures, in: Physics and Simulation of Optoelectronic Devices XXVIII, B. Witzigmann, M. Osiński, Y. Arakawa, eds., 11274 of Proceedings of SPIE, San Francisco, 2020, pp. 1127416/1--1127416/10, DOI 10.1117/12.2551055 .
-
J. Fuhrmann, D.H. Doan, A. Glitzky, M. Liero, G. Nika, Unipolar drift-diffusion simulation of S-shaped current-voltage relations for organic semiconductor devices, in: Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, R. Klöfkorn, E. Keilegavlen, F.A. Radu, J. Fuhrmann, eds., 323 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, pp. 625--633, DOI 10.1007/978-3-030-43651-3_59 .
Abstract
We discretize a unipolar electrothermal drift-diffusion model for organic semiconductor devices with Gauss--Fermi statistics and charge carrier mobilities having positive temperature feedback. We apply temperature dependent Ohmic contact boundary conditions for the electrostatic potential and use a finite volume based generalized Scharfetter-Gummel scheme. Applying path-following techniques we demonstrate that the model exhibits S-shaped current-voltage curves with regions of negative differential resistance, only recently observed experimentally. -
M. Kantner, Th. Koprucki, Non-isothermal Scharfetter--Gummel scheme for electro-thermal transport simulation in degenerate semiconductors, in: Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, R. Klöfkorn, E. Keilegavlen, F.A. Radu, J. Fuhrmann, eds., 323 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, pp. 173--182, DOI 10.1007/978-3-030-43651-3_14 .
Abstract
Electro-thermal transport phenomena in semiconductors are described by the non-isothermal drift-diffusion system. The equations take a remarkably simple form when assuming the Kelvin formula for the thermopower. We present a novel, non-isothermal generalization of the Scharfetter--Gummel finite volume discretization for degenerate semiconductors obeying Fermi--Dirac statistics, which preserves numerous structural properties of the continuous model on the discrete level. The approach is demonstrated by 2D simulations of a heterojunction bipolar transistor. -
M. Kantner, A. Mielke, M. Mittnenzweig, N. Rotundo, Mathematical modeling of semiconductors: From quantum mechanics to devices, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 269--293, DOI 10.1007/978-3-030-33116-0 .
Abstract
We discuss recent progress in the mathematical modeling of semiconductor devices. The central result of this paper is a combined quantum-classical model that self-consistently couples van Roosbroeck's drift-diffusion system for classical charge transport with a Lindblad-type quantum master equation. The coupling is shown to obey fundamental principles of non-equilibrium thermodynamics. The appealing thermodynamic properties are shown to arise from the underlying mathematical structure of a damped Hamitlonian system, which is an isothermal version of socalled GENERIC systems. The evolution is governed by a Hamiltonian part and a gradient part involving a Poisson operator and an Onsager operator as geoemtric structures, respectively. Both parts are driven by the conjugate forces given in terms of the derivatives of a suitable free energy. -
M. Kantner, A generalized Scharfetter--Gummel scheme for degenerate and non-isothermal semiconductors, in: Proceedings of the 19th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2019, J. Piprek, K. Hinzer, eds., IEEE Conference Publications Management Group, Piscataway, 2019, pp. 7--8, DOI 10.1109/NUSOD.2019.8806839 .
Abstract
We present a highly accurate generalization of the Scharfetter--Gummel scheme for the discretization of the currentdensities in degenerate semiconductors under non-isothermalconditions. The underlying model relies on the Kelvin formula forthe Seebeck coefficient, which has the intriguing property that the?T-term in the electrical current density expressions vanishesexactly when passing to the drift-diffusion form ? even thoughthe thermoelectric cross-coupling is fully taken into account. -
M. Kantner, Hybrid modeling of quantum light emitting diodes: Self-consistent coupling of drift-diffusion, Schrödinger--Poisson, and quantum master equations, in: Proc. SPIE 10912, B. Witzigmann, M. Osiński, Y. Arakawa, eds., Physics and Simulation of Optoelectronic Devices XXVII, SPIE Digital Library, Bellingham, 2019, pp. 10912OU/1--10912OU/8, DOI 10.1117/12.2515209 .
Abstract
The device-scale simulation of electrically driven solid state quantum light emitters, such as single-photon sources and nanolasers based on semiconductor quantum dots, requires a comprehensive modeling approach, that combines classical device physics with cavity quantum electrodynamics. In a previous work, we have self-consistently coupled the semi-classical drift-diffusion system with a Markovian quantum master equation in Lindblad form to describe (i) the spatially resolved current injection into a quantum dot embedded within a semiconductor device and (ii) the fully quantum mechanical light-matter interaction in the coupled quantum dot-photon system out of one box. In this paper, we extend our hybrid quantum-classical modeling approach by including a Schroedinger?Poisson problem to account for energy shifts of the quantum dot carriers in response to modifications of its macroscopic environment (e.g., quantum confined Stark effect due to the diode's internal electric field and plasma screening). The approach is demonstrated by simulations of a single-photon emitting diode. -
M. Kantner, Simulation of quantum light sources using the self-consistently coupled Schrödinger--Poisson-Drift-Diffusion-Lindblad system, in: Proceedings of the 19th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2019, J. Piprek, K. Hinzer, eds., IEEE Conference Publications Management Group, Piscataway, 2019, pp. 15--16, DOI 10.1109/NUSOD.2019.8806839 .
Abstract
The device-scale simulation of electrically drivenquantum light sources based on semiconductor quantum dotsrequires a combination of the (classical) semiconductor deviceequations with cavity quantum electrodynamics. In this paper, weextend our previously developed hybrid quantum-classical modelsystem ? where we have coupled the drift-diffusion system witha Lindblad-type quantum master equation ? by including a self-consistent Schrödinger?Poisson problem. The latter describes the(quasi-)bound states of the quantum dot carriers. The extendedmodel allows to describe the bias-dependency of the emissionspectrum due to the quantum confined Stark effect -
M. Lübbering, J. Kunkel, P. Farrell, What company does my news article refer to? Tackling multiclass problems with topic modeling, in: CEUR-WS.org/Vol-2454/paper_41, CEUR-WS.org, Sun SITE Central Europe RWTH Aachen, Aachen, 2019, pp. 353--364, DOI 10.20347/WIAS.PREPRINT.2621 .
Abstract
While it is technically trivial to search for the company name to predict the company a new article refers to, it often leads to incorrect results. In this article, we compare the two approaches bag-of-words with k-nearest neighbors and Latent Dirichlet Allocation with k-nearest neighbor by assessing their applicability for predicting the S&P 500 company which is mentioned in a business news article or press release. Both approaches are evaluated on a corpus of 13k documents containing 84% news articles and 16% press releases. While the bag-of-words approach yields accurate predictions, it is highly inefficient due to its gigantic feature space. The Latent Dirichlet Allocation approach, on the other hand, manages to achieve roughly the same prediction accuracy (0.58 instead of 0.62) but reduces the feature space by a factor of seven. -
TH. Koprucki, A. Maltsi, T. Niermann, T. Streckenbach, K. Tabelow, J. Polzehl, On a database of simulated TEM images for In(Ga)As/GaAs quantum dots with various shapes, in: Proceedings of the 19th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2019, J. Piprek, K. Hinze, eds., IEEE Conference Publications Management Group, Piscataway, 2019, pp. 13--14, DOI 10.1109/NUSOD.2019.8807025 .
-
A. Maltsi, Th. Koprucki, T. Niermann, T. Streckenbach, K. Tabelow, Model-based geometry reconstruction of quantum dots from TEM, in: 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), 18 of Proceedings in Applied Mathematics and Mechanics (PAMM), Wiley-VCH, Weinheim, 2018, pp. e201800398/1--e201800398/2, DOI 10.1002/pamm.201800398 .
-
M. Kantner, M. Mittnenzweig, Th. Koprucki, A hybrid quantum-classical modeling approach for electrically driven quantum dot devices, in: Proc. SPIE 10526, Physics and Simulation of Optoelectronic Devices XXVI, B. Witzigmann, M. Osiński, Y. Arakawa, eds., SPIE Digital Library, 2018, pp. 1052603/1--1052603/6, DOI 10.1117/12.2289185 .
Abstract
The design of electrically driven quantum light sources based on semiconductor quantum dots, such as singlephoton emitters and nanolasers, asks for modeling approaches combining classical device physics with cavity quantum electrodynamics. In particular, one has to connect the well-established fields of semi-classical semiconductor transport theory and the theory of open quantum systems. We present a first step in this direction by coupling the van Roosbroeck system with a Markovian quantum master equation in Lindblad form. The resulting hybrid quantum-classical system obeys the fundamental laws of non-equilibrium thermodynamics and provides a comprehensive description of quantum dot devices on multiple scales: It enables the calculation of quantum optical figures of merit (e.g. the second order intensity correlation function) together with the spatially resolved simulation of the current flow in realistic semiconductor device geometries in a unified way. -
M. Kantner, M. Mittnenzweig, Th. Koprucki, Modeling and simulation of electrically driven quantum light sources: From classical device physics to open quantum systems, in: 14th International Conference on Nonlinear Optics and Excitation Kinetics in Semiconductors, September 23--27, 2018, Berlin, Germany (Conference Program), 2018, pp. 135.
-
M. Patriarca, P. Farrell, J. Fuhrmann, Th. Koprucki, M. Auf DER Maur, Highly accurate discretizations for non-Boltzmann charge transport in semiconductors, in: Proceedings of the 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), A. Djurišić, J. Piprek, eds., IEEE Conference Publications Management Group, Piscataway, NJ, 2018, pp. 53--54.
-
TH. Koprucki, A. Maltsi, T. Niermann, T. Streckenbach, K. Tabelow, J. Polzehl, Towards model-based geometry reconstruction of quantum dots from TEM, in: Proceedings of the 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), A. Djurišić, J. Piprek, eds., IEEE Conference Publications Management Group, Piscataway, NJ, 2018, pp. 115--116.
-
O. Marquardt, P. Mathé, Th. Koprucki, M. Caro, M. Willatzen, Data-driven electronic structure calculations in semiconductor nanostructures -- beyond the eight-band k.p formalism, in: Proceedings of the 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), A. Djurišić, J. Piprek, eds., IEEE Conference Publications Management Group, Piscataway, NJ, 2018, pp. 55--56.
-
M. Liero, A. Fischer, J. Fuhrmann, Th. Koprucki, A. Glitzky, A PDE model for electrothermal feedback in organic semiconductor devices, in: Progress in Industrial Mathematics at ECMI 2016, P. Quintela, P. Barral, D. Gómez, F.J. Pena, J. Rodrígues, P. Salgado, M.E. Vázquez-Méndez, eds., 26 of Mathematics in Industry, Springer International Publishing AG, Cham, 2017, pp. 99--106.
-
M. Liero, J. Fuhrmann, A. Glitzky, Th. Koprucki, A. Fischer, S. Reineke, Modeling and simulation of electrothermal feedback in large-area organic LEDs, in: Proceedings of the 17th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2017, J. Piprek, M. Willatzen, eds., IEEE Conference Publications Management Group, Piscataway, 2017, pp. 105--106, DOI 10.1109/NUSOD.2017.8010013 .
-
M. Bulíček, A. Glitzky, M. Liero, Thermistor systems of p(x)-Laplace-type with discontinuous exponents via entropy solutions, in: PDE 2015: Theory and Applications of Partial Differential Equations, H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., 10 of Discrete and Continuous Dynamical Systems, Series S, no. 4, American Institute of Mathematical Sciences, Springfield, 2017, pp. 697--713.
Abstract
We show the existence of solutions to a system of elliptic PDEs, that was recently introduced to describe the electrothermal behavior of organic semiconductor devices. Here, two difficulties appear: (i) the elliptic term in the current-flow equation is of p(x)-Laplacian-type with discontinuous exponent p, which limits the use of standard methods, and (ii) in the heat equation, we have to deal with an a priori L1 term on the right hand side describing the Joule heating in the device. We prove the existence of a weak solution under very weak assumptions on the data. Our existence proof is based on Schauder's fixed point theorem and the concept of entropy solutions for the heat equation. Here, the crucial point is the continuous dependence of the entropy solutions on the data of the problem. -
P. Farrell, A. Linke, Uniform second order convergence of a complete flux scheme on nonuniform 1D grids, in: Finite Volumes for Complex Applications VIII -- Methods and Theoretical Aspects, FVCA 8, Lille, France, June 2017, C. Cancès, P. Omnes, eds., 199 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing AG, Cham, 2017, pp. 303--310.
-
P. Farrell, Th. Koprucki, J. Fuhrmann, Comparision of Scharfetter--Gummel flux discretizations under Blakemore statistics, in: Progress in Industrial Mathematics at ECMI 2016, P. Quintela, P. Barral, D. Gómez, F.J. Pena, J. Rodrígues, P. Salgado, M.E. Vázquez-Méndez, eds., 26 of Mathematics in Industry, Springer International Publishing AG, Cham, 2017, pp. 91--98.
-
P. Farrell, Th. Koprucki, J. Fuhrmann, Comparison of consistent flux discretizations for drift diffusion beyond Boltzmann statistics, in: Proceedings of the 17th International Conference on Numerical Simulation of Optoelectronic Devices -- NUSOD 2017, J. Piprek, M. Willatzen, eds., IEEE Conference Publications Management Group, Piscataway, 2017, pp. 219--220, DOI 10.1109/NUSOD.2017.8010070 .
-
M. Kantner, U. Bandelow, Th. Koprucki, H.-J. Wünsche, Multi-scale modelling and simulation of single-photon sources on a device level, in: Euro-TMCS II -- Theory, Modelling & Computational Methods for Semiconductors, 7th -- 9th December 2016, Tyndall National Institute, University College Cork, Ireland, E. O'Reilly, S. Schulz, S. Tomic, eds., Tyndall National Institute, 2016, pp. 65.
-
M. Kantner, U. Bandelow, Th. Koprucki, H.-J. Wünsche, Modeling and numerical simulation of electrically pumped single-photon emitters, in: Proceedings of the 15th International Conference on Numerical Simulation of Optoelectronic Devices 2015, J. Piprek, W. Yuh-Renn, eds., IEEE Conference Publications Management Group, Piscataway, 2015, pp. 151--152.
-
M. Kantner, U. Bandelow, Th. Koprucki, Multi-scale modeling and simulation of single-photon sources, in: Proceedings of iNOW 2015 (International Nano-Optoelectronics Workshop) (PDF only), Y. Arakawa, F. Koyama, C. Chang-Hasnain, D. Bimberg, eds., pp. 129-130.
-
D. Peschka, M. Thomas, A. Glitzky, R. Nürnberg, K. Gärtner, M. Virgilio, S. Guha, Th. Schröder, G. Capellini, Th. Koprucki, On device concepts for CMOS-compatible edge-emitters based on strained germanium, in: Proceedings of the 15th International Conference on Numerical Simulation of Optoelectronic Devices 2015, J. Piprek, W. Yuh-Renn, eds., IEEE Conference Publications Management Group, Piscataway, 2015, pp. 129--130.
-
A. Fischer, Th. Koprucki, A. Glitzky, M. Liero, K. Gärtner, J. Hauptmann, S. Reineke, D. Kasemann, B. Lüssem, K. Leo, R. Scholz, OLEDs: Light-emitting thin film thermistors revealing advanced self-heating effects, in: Organic Light Emitting Materials and Devices XIX, F. So, Ch. Adachi, J.-J. Kim, eds., 9566 of Proc. SPIE, SPIE Digital Library, Bellingham, Washington, 2015, pp. 95661A/1--95661A/7.
Abstract
Large area OLEDs show pronounced Joule self-heating at high brightness. This heating induces brightness inhomogeneities, drastically increasing beyond a certain current level. We discuss this behavior considering 'S'-shaped negative differential resistance upon self-heating, even allowing for 'switched-back' regions where the luminance finally decreases (Fischer et al., Adv. Funct. Mater. 2014, 24, 3367). By using a multi-physics simulation the device characteristics can be modeled, resulting in a comprehensive understanding of the problem. Here, we present results for an OLED lighting panel considered for commercial application. It turns out that the strong electrothermal feedback in OLEDs prevents high luminance combined with a high degree of homogeneity unless new optimization strategies are considered. -
G. Capellini, M. Virgilio, Y. Yamamoto, L. Zimmermann, B. Tillack, D. Peschka, M. Thomas, A. Glitzky, R. Nürnberg, K. Gärtner, Th. Koprucki, Th. Schroeder, Modeling of an edge-emitting strained-Ge laser, in: Advanced Solid State Lasers, OSA Technical Digest (online) (Optical Society of America, 2015), 2015, pp. ATu2A.19/1--ATu2A.19/3.
Abstract
By using fully-coupled 2D optoelectronic simulations with embedded microscopic gain calculations, we study the optoelectronic performance of a monolithically integrated edge-emitting laser based on strained germanium microstrips fabricated using CMOS standard processes. -
TH. Koprucki, M. Kantner, J. Fuhrmann, K. Gärtner, On modifications of the Scharfetter--Gummel scheme for drift-diffusion equations with Fermi-like statistical distribution functions, in: Proceedings of the 14th International Conference on Numerical Simulation of Optoelectronic Devices, NUSOD 2014, 1--4 September 2014, J. Piprek, J. Javaloyes, eds., IEEE Conference Publications Management Group, Piscataway, NJ, USA, 2014, pp. 155--156.
-
V. Mehrmann, A. Mielke, F. Schmidt, D -- Electronic and photonic devices, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 229--232.
-
TH. Koprucki, K. Gärtner, Generalization of the Scharfetter--Gummel scheme, in: Proceedings of the 13th International Conference on Numerical Simulation of Optoelectronic Devices, NUSOD 2013, 19--22 August 2013, J. Piprek, L. Chrostowski, eds., IEEE Conference Publications Management Group, Piscataway, NJ, USA, 2013, pp. 85--86.
-
A. Glitzky, K. Gärtner, J. Fuhrmann, Th. Koprucki, A. Fischer, B. Lüssem, K. Leo, R. Scholz, Electro-thermal modeling of organic semiconductors describing negative differential resistance induced by self-heating, in: Proceedings of the 13th International Conference on Numerical Simulation of Optoelectronic Devices, NUSOD 2013, 19--22 August 2013, J. Piprek, L. Chrostowski, eds., IEEE Conference Publications Management Group, Piscataway, NJ, USA, 2013, pp. 77--78.
-
TH. Koprucki, K. Gärtner, Discretization scheme for drift-diffusion equations with strong diffusion enhancement, in: Proceedings of the 12th International Conference on Numerical Simulation of Optoelectronic Devices, NUSOD'12, J. Piprek, W. Lu, eds., IEEE Conference Publications Management Group, New Jersey, USA, 2012, pp. 103--104.
-
U. Bandelow, Th. Koprucki, A. Wilms, A. Knorr, Multi-species modeling of quantum dot lasers with microscopic treatment of Coulomb scattering, in: Proceedings of the 10th International Conference on Numerical Simulation of Optoelectronic Devices, NUSOD 2010, J. Piprek, B. Klein, D. Yoder, eds., IEEE, Piscataway, NJ, USA, 2010, pp. 59--60.
-
P.N. Racec, R. Racec, H. Neidhardt, R-matrix formalism for electron scattering in two dimensions with applications to nanostructures with quantum dots, in: Trends in Nanophysics, A. Aldea, V. Bârsan, eds., Engineering Materials, Springer, Berlin/Heidelberg, 2010, pp. 149--174.
Abstract
We investigate the scattering phenomena in two dimensions produced by a general finite-range nonseparable potential. This situation can appear either in a Cartesian geometry or in a heterostructure with cylindrical symmetry. Increasing the dimensionality of the scattering problem new processes as the scattering between conducting channels and the scattering from conducting to evanescent channels are allowed. For certain values of the energy, called resonance energy, the transmission through the scattering region changes dramatically in comparison with an one-dimensional problem. If the potential has an attractive character even the evanescent channels can be seen as dips of the total transmission. The multi-channel current scattering matrix is determined using its representation in terms of the R-matrix. The resonant transmission peaks are characterized quantitatively through the poles of the current scattering matrix. Detailed maps of the localization probability density sustain the physical interpretation of the resonances. Our formalism is applied to a quantum dot in a two dimensional electron gas and a conical quantum dot embedded inside a nanowire. -
S. Ahmed, M. Usman, C. Heitzinger, R. Rahman, A. Schliwa, G. Klimeck, Symmetry breaking and fine structure splitting in zincblende quantum dots: Atomistic simulations of long-range strain and piezoelectric field, in: Physics of Semiconductors, W. Jantsch, F. Schäffler, eds., 893 of AIP Conference Proceedings, Springer, Berlin [et al.], 2007, pp. 849--850.
-
J. Behrndt, H. Neidhardt, J. Rehberg, Block matrices, optical potentials, trace class perturbations and scattering, in: Operator Theory in Inner Product Spaces, K.-H. Förster, P. Jonas, H. Langer, C. Trunk, eds., 175 of Operator Theory: Advances and Applications, Birkhäuser, Basel, 2007, pp. 33--49.
-
C. Cornet, M. Hayne, A. Schliwa, F. Doré, C. Labbé, H. Folliot, J. Even, D. Bimberg, Theory and experiment of InAs/InP quantum dots: From calculations to laser emission, in: Physics of Semiconductors, W. Jantsch, F. Schäffler, eds., 893 of AIP Conference Proceedings, Springer, Berlin [et al.], 2007, pp. 779--780.
-
F. Doré, C. Cornet, A. Schliwa, N. Bertru, O. Dehaese, I. Alghoraibi, H. Folliot, R. Piron, A. Le Corre, A theoretical and experimental study of $>2 mu$m luminescence of quantum dots on InP substrate, in: Physics of Semiconductors, W. Jantsch, F. Schäffler, eds., 893 of AIP Conference Proceedings, Springer, Berlin [et al.], 2007, pp. 889--890.
-
U. Wulf, P.N. Racec, H. Richter, Quantentransport in Nanotransistoren, in: vol. 90 (2007) of Sitzungsberichte der Leibniz-Sozietät, traem fo verlag dr. wolfgang weist, Berlin, pp. 121--137.
-
A. Glitzky, Energy models where the equations are defined on different domains, in: GAMM Annual Meeting 2006 -- Berlin, Special Issue (Vol. 6, Issue 1) of PAMM (Proceedings of Applied Mathematics and Mechanics), Wiley-VCH Verlag, Weinheim, 2006, pp. 629--630.
-
H. Gajewski, H.-Chr. Kaiser, H. Langmach, R. Nürnberg, R.H. Richter, Mathematical modelling and numerical simulation of semiconductor detectors, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 355--364.
-
R. Hünlich, G. Albinus, H. Gajewski, A. Glitzky, W. Röpke, J. Knopke, Modelling and simulation of power devices for high-voltage integrated circuits, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 401--412.
-
H.-Chr. Kaiser, U. Bandelow, Th. Koprucki, J. Rehberg, Modelling and simulation of strained quantum wells in semiconductor lasers, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 377--390.
-
U. Bandelow, H. Gajewski, H.-Chr. Kaiser, Modeling combined effects of carrier injection, photon dynamics and heating in Strained Multi-Quantum-Well Laser, in: Physics and Simulation of Optoelectronic Devices VIII, R.H. Binder, P. Blood, M. Osinski, eds., 3944 of Proceedings of SPIE, SPIE, Bellingham, WA, 2000, pp. 301--310.
-
R. Hünlich, A. Glitzky, On energy estimates for electro-diffusion equations arising in semiconductor technology, in: Partial differential equations. Theory and numerical solution, W. Jäger, J. Nečas, O. John, K. Najzar, eds., 406 of Chapman & Hall Research Notes in Mathematics, Chapman & Hall, Boca Raton, FL, 2000, pp. 158--174.
-
H.-Chr. Kaiser, J. Rehberg, About some mathematical questions concerning the embedding of Schrödinger-Poisson systems into the drift-diffusion model of semiconductor devices, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1328--1333.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
L. Ermoneit, A. Thayil, Th. Koprucki, M. Kantner, Exact multi-valley envelope function theory of valley splitting in Si/SiGe nanostructures, Preprint no. 3260, WIAS, Berlin, 2026, DOI 10.20347/WIAS.PREPRINT.3260 .
PDF (9575 kByte) -
A. Thayil, L. Ermoneit, L.R. Schreiber, Th. Koprucki, M. Kantner, Optimization of Si/SiGe heterostructures for large and robust valley splitting in silicon qubits, Preprint no. 3249, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3249 .
Abstract, PDF (7243 kByte)
The notoriously low and fluctuating valley splitting is one of the key challenges for electron spin qubits in silicon (Si), limiting the scalability of Si-based quantum processors. In silicon-germanium (SiGe) heterostructures, the problem can be addressed by the design of the epitaxial layer stack. Several heuristic strategies have been proposed to enhance the energy gap between the two nearly degenerate valley states in strained Si/SiGe quantum wells (QWs), emphe.g., sharp Si/SiGe interfaces, Ge spikes or oscillating Ge concentrations within the QW. In this work, we develop a systematic variational optimization approach to compute optimal Ge concentration profiles that boost selected properties of the intervalley coupling matrix element. Our free-shape optimization approach is augmented by a number of technological constraints to ensure feasibility of the resulting epitaxial profiles. The method is based on an effective mass type envelope function theory accounting for the effects of strain and compositional alloy disorder. Various previously proposed heterostructure designs are recovered as special cases of the constrained optimization problem. Our main result is a novel heterostructure design we refer to as the emphmodulated wiggle well, which provides a large deterministic enhancement of the valley splitting along with a reliable suppression of the disorder-induced volatility. In addition, our new design offers a wide-range tunability of the valley splitting controlled by the vertical electric field, which offers new perspectives to engineer switchable qubits with on-demand adjustable valley splitting. -
A. Glitzky, M. Liero, Drift-diffusion models with nonlinear boundary conditions modeling Schottky contacts at metal-semiconductor interfaces, Preprint no. 3242, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3242 .
Abstract, PDF (345 kByte)
The paper deals with drift-diffusion models for semiconductor heterostructures with Schottky contacts at all metal-semiconductor interfaces. Our analytical investigations allow for Boltzmann as well as Fermi--Dirac statistics for the charge-carrier densities. We verify the existence and boundedness of weak solutions of the instationary van Roosbroeck system in this context. Moreover, under additional assumptions the uniqueness and the higher regularity of the solution are demonstrated. Here, higher regularity results for scalar quasilinear parabolic PDEs are used. -
N. Ciroth, A. Sala, R. Xue, L. Ermoneit, Th. Koprucki, M. Kantner, L.R. Schreiber, Numerical simulation of coherent spin-shuttling in a QuBus with charged defects, Preprint no. 3241, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3241 .
Abstract, PDF (874 kByte)
Recent advances in coherent conveyor-mode spin qubit shuttling are paving the way for large scale quantum computing platforms with qubit connectivity achieved by spin qubit shuttles. We developed a simulation tool to investigate numerically the impact of device imperfections on the spin-coherence of conveyor-mode shuttling in Si/SiGe. We simulate the quantum evolution of a mobile electron spin-qubit under the influence of sparse and singly charged point defects placed in the Si/SiGe heterostructure in close proximity to the shuttle lane. We consider different locations of a single charge defect with respect to the center of the shuttle lane, multiple orbital states of the electron in the shuttle with g-factor differences between the orbital levels, and orbital relaxation induced by electron-phonon interaction. With this simulation framework, we identify the critical defect density of charged point defects in the heterostructure for conveyor-mode spin qubit shuttle devices and quantify the impact of a single defect on the coherence of a qubit. -
A. Thayil, L. Ermoneit, M. Kantner, Theory of valley-splitting in Si/SiGe spin-qubits: Interplay of strain, resonances and random alloy disorder, Preprint no. 3158, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3158 .
PDF (5807 kByte) -
L. Ermoneit, B. Schmidt, Th. Koprucki, J. Fuhrmann, T. Breiten, A. Sala, N. Ciroth, R. Xue, L.R. Schreiber, M. Kantner, Optimal control of conveyor-mode spin-qubit shuttling in a Si/SiGe quantum bus in the presence of charged defects, Preprint no. 3082, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3082 .
PDF (9473 kByte) -
K.M. Gambaryan, O. Ernst, T. Boeck, O. Marquardt, Energy level alignment of confined hole states in $InAs_1-x-ySb_xP_y$ double quantum dots, Preprint no. 3040, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3040 .
Abstract, PDF (310 kByte)
We present a combined experimental and theoretical study of uncapped In(As,Sb,P) double quantum dots (DQD), suited for application in novel resonant tunneling nanodiods or single-photon nanooptical up- and down-converters in the mid-infrared spectral range. We provide details on the growth process using liquid-phase epitaxy (LPE), as well as on the characterization using atomic-force microscopy (AFM) and scanning electron microscopy (SEM). We find that most DQDs exhibit an asymmetry such that the two QDs of each pair have different dimensions, giving rise to correspondingly different quantum confinement of hole states localized in each QD. Based on these data, we have performed systematic simulations based on an eight-band $mathbfkcdotmathbfp$ model to identify the relationship between QD dimensions and the energy difference between corresponding confined hole states in the two QDs. Finally, we have determined the strength of an applied electric field required to energetically align the hole ground states of two QDs of different dimensions in order to facilitate hole tunneling. -
K.M. Gambaryan, O. Marquardt, T. Boeck, A. Trampert, Micro- and nano-scale engineering and structures shape architecture at nucleation from In-As-Sb-P composition liquid phase on an InAs(100) surface, Preprint no. 2775, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2775 .
Abstract, PDF (4287 kByte)
In this review paper we present results of the growth, characterization and electronic properties of In(As,Sb,P) composition strain-induced micro- and nanostructures. Nucleation is performed from In-As-Sb-P quaternary composition liquid phase in Stranski--Krastanow growth mode using steady-state liquid phase epitaxy. Growth features and the shape transformation of pyramidal islands, lens-shape and ellipsoidal type-II quantum dots (QDs), quantum rings and QD-molecules are under consideration. It is shown that the application of a quaternary In(As,Sb,P) composition wetting layer allows not only more flexible control of lattice-mismatch between the wetting layer and an InAs(100) substrate, but also opens up new possibilities for nanoscale engineering and nanoarchitecture of several types of nanostructures. HR-SEM, AFM, TEM and STM are used for nanostructure characterization. Optoelectronic properties of the grown structures are investigated by FTIR and photoresponse spectra measurements. Using an eight-band $mathbfkcdotmathbfp$ model taking strain and built-in electrostatic potentials into account, the electronic properties of a wide range of InAs$_1-x-y$Sb$_x$P$_y$ QDs and QD-molecules are computed. Two types of QDs mid-infrared photodetectors are fabricated and investigated. It is shown that the incorporation of QDs allows to improve some output device characteristics, in particularly sensitivity, and to broaden the spectral range. -
M. Lübbering, J. Kunkel, P. Farrell, What company does my news article refer to? Tackling multiclass problems with topic modeling, Preprint no. 2621, WIAS, Berlin, 2019, DOI 10.20347/WIAS.PREPRINT.2621 .
Abstract, PDF (354 kByte)
While it is technically trivial to search for the company name to predict the company a new article refers to, it often leads to incorrect results. In this article, we compare the two approaches bag-of-words with k-nearest neighbors and Latent Dirichlet Allocation with k-nearest neighbor by assessing their applicability for predicting the S&P 500 company which is mentioned in a business news article or press release. Both approaches are evaluated on a corpus of 13k documents containing 84% news articles and 16% press releases. While the bag-of-words approach yields accurate predictions, it is highly inefficient due to its gigantic feature space. The Latent Dirichlet Allocation approach, on the other hand, manages to achieve roughly the same prediction accuracy (0.58 instead of 0.62) but reduces the feature space by a factor of seven. -
R. Schlundt, A multilevel Schur complement preconditioner with ILU factorization for complex symmetric matrices, Preprint no. 2556, WIAS, Berlin, 2018, DOI 10.20347/WIAS.PREPRINT.2556 .
Abstract, PDF (318 kByte)
This paper describes a multilevel preconditioning technique for solving complex symmetric sparse linear systems. The coefficient matrix is first decoupled by domain decomposition and then an approximate inverse of the original matrix is computed level by level. This approximate inverse is based on low rank approximations of the local Schur complements. For this, a symmetric singular value decomposition of a complex symmetric matix is used. The block-diagonal matrices are decomposed by an incomplete LDLT factorization with the Bunch-Kaufman pivoting method. Using the example of Maxwell's equations the generality of the approach is demonstrated. -
J. Rehberg, A criterion for a two-dimensional domain to be Lipschitzian, Preprint no. 1695, WIAS, Berlin, 2012, DOI 10.20347/WIAS.PREPRINT.1695 .
Abstract, Postscript (187 kByte), PDF (64 kByte)
We prove that a two-dimensional domain is already Lipschitzian if only its boundary admits locally a one-dimensional, bi-Lipschitzian parametrization.
 Talks, Poster
Talks, Poster
-
P. Farrell, Charge transport in perovskite solar cells: modeling, analysis and simulations, Seminar, Universität Potsdam, Soft Matter Physics and Optoelectronics, February 6, 2026.
-
P. Farrell, Mathematical Modeling, Analysis and Simulation of Innovative Multiphysics Semiconductor Devices, Seminarvortrag, RWTH Aachen, Fachgruppe Mathematik, Lehr- und Forschungsgebiet Diskrete Optimierung, February 23, 2026.
-
D. Abdel, Charge transport in perovskite solar cells: Modelling, analysis and simulations, Workshop on Mathematical Models for Quantum and Semiclassical Dynamics, September 10 - 12, 2025, University of Florence, Department of Mathematics and Informatics Ülisse Dini", Italy, September 12, 2025.
-
D. Abdel, Charge transport in perovskite solar cells: modelling, numerical analysis and simulations, Mini-workshop ARISE, Inria center at the University of Lille, Villeneuve d'Ascq, France, June 17, 2025.
-
Z. Elsayed Amer, Modeling and simulation of a coupled van Roosbroeck--Helmholtz System, Workshop on Mathematical Models for Quantum and Semiclassical Dynamics, September 10 - 12, 2025, University of Florence, Department of Mathematics and Informatics Ülisse Dini", Italy, September 12, 2025.
-
Z. Elsayed Amer, Numerical methods for a coupled drift-diffusion and Helmholtz model for laser applications, MESIGA25: Numerical Methods in Applied Mathematics, March 11 - 13, 2025, Institut für Mathematik der Universität Potsdam, March 12, 2025.
-
L. Ermoneit, Coherent transport of semiconductor spin-qubits: Modeling, simulation and optimal control (online talk), MATH+ Spotlight talks, January 29, 2025.
-
L. Ermoneit, Optimal control for coherent electron shuttling of a SiGe-quantum bus in the presence of charged defects, DPG-Frühjahrstagung der Sektion Kondensierte Materie (SKM), March 16 - 21, 2025, Universität Regensburg.
-
Y. Hadjimichael, Strain distribution in zincblende and wurtzite nanowires bent by a one-sided stressor shell, Leibniz MMS Days 2025, March 26 - 28, 2025, The Leibniz Research Network "Mathematical Modeling and Simulation", Leibniz Institute for Baltic Sea Research Warnemünde (IOW), March 27, 2025.
-
M. O'Donovan, Developing a multi-scale drift-diffusion simulation framework for UV-C emitting quantum well systems, Analysis of Robust Numerical Solvers for Innovative Semiconductors in View of Energy Transition (ARISE 2025), November 4 - 5, 2025, WIAS Berlin, November 4, 2025.
-
M. O'Donovan, Multi-scale hybrid band simulation of (Al,Ga)N UV-C light emitting diodes, International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2025), September 14 - 18, 2025, Łódź University of Technology, Poland, September 15, 2025.
-
M. O'Donovan, Simulation of (Al,Ga)N-based UV LEDs including effects from disorder, 15th International Conference on Nitride Semiconductors (ICNS 15), Sweden, July 6 - 11, 2025.
-
A. Glitzky, A uniqueness result for a drift-diffusion model for perovskite solar cells, Analysis of Robust Numerical Solvers for Innovative Semiconductors in View of Energy Transition (ARISE 2025), November 4 - 5, 2025, WIAS Berlin, November 4, 2025.
-
TH. Eiter, Regularizations and energy-variational solutions for a visco-elasto-plastic semicompressible fluid model, SCCS Days 2025 of the Collaborative Research Center -- CRC 1114 ``Scaling Cascades in Complex Systems'', November 5 - 6, 2025, Zuse-Institut Berlin, November 5, 2025.
-
P. Farrell, Numerische Methoden für innovative Halbleiterbauteile, Transfer Workshop: ErUM-Scientists and Industry in Dialogue, February 6 - 7, 2025, ErUM Data Hub, Aachen, February 6, 2025.
-
P. Farrell, Unravelling the mystery of enhanced open-circuit voltages in nanotextured perovskite solar cells, Kaiserslautern Applied and Industrial Mathematics Days - KLAIM 2025, October 6 - 8, 2025, Fraunhofer-Institut für Techno- und Wirtschaftsmathematik ITWM, Kaiserslautern, October 7, 2025.
-
J. Fuhrmann, Continuum scale electrolyte simulations based on finite volume methods, Bridging the Gap II: Transitioning from Deterministic to Stochastic Interaction Modeling in Electrochemistry, September 3 - December 12, 2025, Institute for Pure and Applied Mathematics, University of California, Los Angeles, USA, October 8, 2025.
-
J. Fuhrmann, LiquidElectrolytes.jl - A generalized Poisson-Nernst-Planck solver written in Juli, ModVal 2025 - 21st Symposium on Modeling and Experimental Validation of Electrochemical Energy Technologies, Karlsruhe, March 10 - 12, 2025.
-
J. Fuhrmann, Thermodynamically consistent finite volume methods for generalized Nernst--Planck--Poisson problems, Bridging the Gap: Transitioning from Deterministic to Stochastic Interaction Modeling in Electrochemistry, September 3 - December 12, 2025, Institute for Pure and Applied Mathematics, University of California, Los Angeles, USA, September 9, 2025.
-
TH. Koprucki, Semiconductor modeling and simulation: Bridging mathematics, physics, and engineering, Award Ceremony for IHP's Junior Research Group, Leibniz-Institut für innovative Mikroelektronik, Frankfurt (Oder), June 3, 2025.
-
M. Landstorfer, Continuum thermodynamic models for electrochemical interfaces, Bridging the Gap II: Transitioning from Deterministic to Stochastic Interaction Modeling in Electrochemistry, September 3 - December 12, 2025, Institute for Pure and Applied Mathematics, University of California, Los Angeles, USA, October 8, 2025.
-
Z. Amer, Numerical methods for coupled drift-diffusion and Helmholtz Models for laser applications, International Conference on Simulation of Organic Electronics and Photovoltaics, SimOEP, September 2 - 4, 2024, ZHAW - Zurich University of Applied Sciences, Winterthur, Switzerland, September 4, 2024.
-
CH. Keller, A drift-diffusion model to describe ion channel dynamics, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), Berlin, September 10 - 13, 2024.
-
L. Ermoneit, B. Schmidt, A. Sala, N. Ciroth, L. Schreiber, T. Breiten, Th. Koprucki, M. Kantner, Simulation and optimal control of single-electron shuttling in a SiGe quantum bus, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), Berlin, September 10 - 13, 2024.
-
L. Ermoneit, B. Schmidt, J. Fuhrmann, A. Sala, N. Ciroth, L. Schreiber, T. Breiten, Th. Koprucki, M. Kantner, Optimal control of a Si/SiGe quantum bus for scalable quantum computing architectures, Quantum Optimal Control: From Mathematical Foundations to Quantum Technologies, MATH+, Berlin, May 21, 2024.
-
L. Ermoneit, B. Schmidt, Th. Koprucki, T. Breiten, M. Kantner, Coherent transport of semiconductor spin-qubits: Modeling, simulation and optimal control, MATH+ Day 2024, Urania Berlin, October 2, 2024.
-
L. Ermoneit, Optimal control of a SiGe-Quantum bus for coherent electron shuttling in the presence of material defects, APS March Meeting, March 3 - 8, 2024, Minneapolis, USA, March 7, 2024.
-
Y. Hadjimichael, An energy-based finite-strain model for 3D heterostructured materials, Leibniz MMS Days 2024, April 10 - 12, 2024, Leibniz Network "Mathematical Modeling and Simulation", Leibniz Institut für Verbundwerkstoffe GmbH (IVW), Kaiserslautern, April 11, 2024.
-
L. Mertenskötter, Data-driven stochastic modeling of semiconductor lasers (online talk), MATH+ Spotlight talks, December 20, 2024.
-
M. O'Donovan, Multi-scale simulation of electronic and transport properties in (Al,Ga)N quantum well systems for UV-C emission, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), September 10 - 13, 2024, WIAS Berlin, September 11, 2024.
-
M. O'Donovan, Simulation of the alloy fluctuations on luminescence and transport in AIGaN-based UV-LEDs, XXXV. Heimbach Workshop, September 23 - 27, 2024, Technische Universität Berlin, Mansfeld, September 26, 2024.
-
M. O'Donovan, Theoretical investigations on different scales towards novel III-N materials and devices, Roundtable discussion of the SPP 2477 ``Nitrides4Future'', Magdeburg, September 24 - 25, 2024.
-
A. Thayil, Optimization of valley splitting in Si/SiGe spin qubits, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), September 10 - 13, 2024, WIAS Berlin, September 12, 2024.
-
N. Ciroth, A. Sala, L. Ermoneit, Th. Koprucki, M. Kantner, L. Schreiber, Numerical simulation of coherent spin-shuttling in silicon devices across dilute charge defects, Silicon Quantum Electronics Workshop 2024, Davos, Switzerland, September 4 - 6, 2024.
-
D. Abdel, Modeling and simulation of vacancy-assisted charge transport in innovative semiconductor devices, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), September 10 - 13, 2024, WIAS Berlin, September 11, 2024.
-
A. Glitzky, Analysis of a drift-diffusion model for perovskite solar cells, 94th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2024), Session 14.07 ``Various Topics in Applied Analysis'', March 18 - 22, 2024, Otto-von-Guericke-Universität Magdeburg, March 21, 2024.
-
A. Glitzky, Electrothermal models for organic semiconductor devices, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), Berlin, September 10 - 13, 2024.
-
A. Maltsi, Introduction to photoacoustic imaging, Women in Math - Introduction of the Iris Runge Program, Weierstraß-Institut für Angewandte Analysis und Stochastik, March 18, 2024.
-
A. Maltsi, The mathematics behind imaging, WINS School 2024: Cross Sections and Interfaces in Science and its Environment, May 31 - June 3, 2024, Humboldt-Universität zu Berlin, Blossin, May 31, 2024.
-
P. Farrell, Charge transport in perovskites solar cells: Modeling, analysis and simulations, Inria-ECDF Partnership Kick-Off Workshop, June 5 - 7, 2024, Inria and the Einstein Center for Digital Future, Berlin, June 7, 2024.
-
J. Fuhrmann, Development of numerical methods and tools for drift-diffusion simulations, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), Berlin, September 10 - 13, 2024.
-
J. Fuhrmann, Finite volume simulations of drift-diffusion problems in semiconductors and electrolytes, Seminar, Laboratoire de Génie des Procédés et Matériaux, Chaire de Biotechnologie de CentraleSupélec, Pomacle, France, September 19, 2024.
-
Y. Hadjimichael, Strain distribution in zincblende and wurtzite GaAs nanowires bent by a one-sided (In,Al)As shell, Applied Mathematics and Simulation for Semiconductor Devices (AMaSiS 2024), Berlin, September 10 - 13, 2024.
-
M. Kantner, L. Ermoneit, B. Schmidt, A. Sala, N. Ciroth, L. Schreiber, Th. Koprucki, Optimal control of conveyor-mode electron shuttling in a Si/SiGe quantum bus in the presence of charged defects, Silicon Quantum Electronics Workshop 2024, Davos, Switzerland, September 4 - 6, 2024.
-
M. Kantner, Conveyor-mode electron shuttling in a Si/SiGe quantum bus: Modeling, simulation, optimization, Focus Workshop on Theory of Spin-Qubit Shuttling, Rheinisch-Westfälische Technische Hochschule Aachen, September 18, 2024.
-
D. Abdel, N.E. Courtier, P. Farrell, Modelling and simulation of charge transport in Perovskite solar cells, SIAM Conference on Computational Science and Engineering (CSE23), Amsterdam, Netherlands, February 26 - March 3, 2023.
-
A. Maltsi, Symmetries in Transmission Electron Microscopy images of semiconductor nanostructures with strain, 23rd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), September 18 - 21, 2023, Politecnico di Torino, Italy, September 21, 2023.
-
A. Maltsi, Symmetries in TEM imaging of semiconductor nanostructures with strain, 15th Annual Meeting Photonic Devices, March 29 - 31, 2023, Zuse-Institut Berlin, March 31, 2023.
-
A. Maltsi, Symmetries in TEM imaging of semiconductor nanostructures with strain, Leibniz MMS Days 2023, April 17 - 19, 2023, Leibniz-Institut für Agrartechnik und Bioökonomie (ATB), Potsdam, April 18, 2023.
-
A. Maltsi, Symmetries in transmission electron microscopy imaging of crystals with strain, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Tokyo, Japan, August 20 - 25, 2023.
-
L. Ermoneit, B. Schmidt, J. Fuhrmann, Th. Koprucki, M. Kantner, Coherent spin-qubit shuttling in a SiGe quantum bus: Device-scale modeling, simulation and optimal control, Leibniz MMS Days 2023, Potsdam, April 17 - 19, 2023.
-
M. O'Donovan, Atomistic study of Urbach tail energies in (Al,Ga)N quantum well systems, 23rd International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2023), September 18 - 21, 2023, Politecnico di Torino, Italy, September 21, 2023.
-
M. O'Donovan, Impact of alloy disorder on carrier transport and recombination in (Al,Ga)N-based UV-C emitters, The 6th International Workshop on Ultraviolet Materials and Devices (IWUMD 2023), June 5 - 8, 2023, Metz Congrès Robert Schuman, France, June 7, 2023.
-
M. O'Donovan, Modeling random alloy fluctuations in carrier transport simulations of III-N based light emitting diodes - Connecting atomistic tight-binding to drift-diffusion, 15th Annual Meeting Photonic Devices, March 29 - 31, 2023, Zuse-Institut Berlin, March 31, 2023.
-
M. O'Donovan, Tight binding simulations of localization in alloy fluctuations in nitride based LEDs, Seminar zu Physik der Gruppe III-Nitrid-Halbleiter und nanophotonischer Bauelemente und Advanced III-Nitride Materials and Photonic Devices (IIIN-MPD), Technische Universität Berlin, AG Experimentelle Nanophysik und Photonik, May 17, 2023.
-
D. Sommer, Robust model predictive control for digital twins using feedback laws, Leibniz MMS Days 2023, April 17 - 19, 2023, Leibniz-Institut für Agrartechnik und Bioökonomie (ATB), Potsdam, April 18, 2023.
-
A. Glitzky, An effective bulk-surface thermistor model for large-area organic light-emitting diodes, 93rd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2023), Session 14 ``Applied Analysis'', May 30 - June 2, 2023, Technische Universität Dresden, May 30, 2023.
-
P. Farrell, Charge transport in Perovskites devices: modeling, numerical analysis and simulations, Workshop on Applied Mathematics: Quantum and Classical Models, Università degli Studi di Firenze, Dipartimento di Matematica e Informatica 'Ulisse Dini', Italy, November 29, 2023.
-
M. Kantner, L. Ermoneit, B. Schmidt, J. Fuhrmann, A. Sala, L.R. Schreiber, Th. Koprucki, Optimal control of a SiGe-quantum bus for coherent electron shuttling in scalable quantum computing architectures, Silicon Quantum Electronics Workshop 2023, Kyoto, Japan, October 31 - November 2, 2023.
-
M. Liero, Luminance inhomogeneities in large-area OLEDs due to electrothermal feedback, Hybride Optoelektronische Materialsysteme (HYD Seminar), Integrative Research Institute for the Sciences (IRIS Adlershof), Hybrid Devices Group, Berlin, April 20, 2023.
-
O. Marquardt, Simulating the electronic properties of semiconductor nanostructures, 5th Leibniz MMS Days, April 25 - 27, 2022, Potsdam-Institut für Klimafolgenforschung (PIK), April 26, 2022.
-
O. Marquardt, SPHInX-Tutorial 2022 (Hybrid Event), March 14 - April 11, 2022, WIAS Berlin.
-
A. Glitzky, A drift-diffusion based electrothermal model for organic thin-film devices including electrical and thermal environment, DMV Annual Meeting 2022, Section 09 ``Applied Analysis and Partial Differential Equations", September 12 - 16, 2022, Freie Universität Berlin, September 14, 2022.
-
D. Fritsch, Identifying and efficiently computing band-edge energies for charge transport simulations in strained materials, MATH+ Day 2022, Technische Universität Berlin, November 18, 2022.
-
M. Liero, Analysis of an electrothermal drift-diffusion model for organic semiconductor devices, PHAse field MEthods in applied sciences (PHAME 2022), May 23 - 27, 2022, Istituto Nazionale di Alta Matematica, Rome, Italy, May 24, 2022.
-
M. Liero, Modeling, analysis, and simulation of electrothermal feedback in organic devices, Audit 2022, September 22 - 23, 2022, Weierstraß-Institut Berlin, September 22, 2022.
-
M. Liero, The impact of modeling, analysis, and simulation on organic semiconductor development (online talk), ERCOM Meeting 2022 (Hybrid Event), March 25 - 26, 2022, European Research Centers on Mathematics, Bilbao, Spain, March 26, 2022.
-
A. Mielke, Existence and longtime behavior of solutions to a degenerate parabolic system, Journées Équations aux Dérivées Partielles 2022, May 30 - June 3, 2022, Centre National de la Recherche Scientifique, Obernai, France, May 31, 2022.
-
D. Abdel, P. Vágner, J. Fuhrmann, P. Farrell, Modeling and simulation of charge transport in perovskite solar cells, AMaSiS 2021: Applied Mathematics and Simulation for Semiconductors and Electrochemical Systems (Online Event), September 6 - 9, 2021.
-
D. Abdel, P. Vágner, J. Fuhrmann, P. Farrell, Modeling and simulation of charge transport in perovskite solar cells, Conference ``Asymptotic Behaviors of Systems of PDEs arising in Physics and Biology: Theoretical and Numerical Points of View'', Lille, Laboratoire Paul Painlevé, France, November 16 - 19, 2021.
-
A. Maltsi, Model-based geometry reconstruction of TEM images, MATH+ Day 2021 (Online Event), Technische Universität Berlin, November 5, 2021.
-
A. Maltsi, On the Darwin--Howie--Whelan equations in TEM imaging (online talk), Young Women in PDEs and Applications (Online Event), September 20 - 22, 2021, Universität Bonn, September 22, 2021.
-
O. Marquardt, Modelling the electronic properties of semiconductor nanowire heterostructures (online talk), PDI-Seminar, Paul-Drude-Institut für Festkörperelektronik, August 23, 2021.
-
G. Nika, Derivation of an effective bulk-surface thermistor model for OLEDs, AMaSiS 2021: Applied Mathematics and Simulation for Semiconductors and Electrochemical Systems (Online Event), September 6 - 9, 2021.
-
P. Vágner , Generalized Nernst--Planck--Poisson model of solid oxide YSZ LSM O_2 electrode interface (online talk), 72nd Annual International Society of Electrochemistry (ISE) Meeting (Online Event), August 29 - September 3, 2021, Seoul National University, Jeju Island, Korea (Republic of), September 3, 2021.
-
P. Vágner , Generalized Nernst--Planck--Poisson model of solid oxide YSZ LSM O_2 electrode interface (online talk), AMaSiS 2021: Applied Mathematics and Simulation for Semiconductors and Electrochemical Systems (Online Event), September 6 - 9, 2021, WIAS Berlin, September 7, 2021.
-
B. Gaudeul, J. Fuhrmann, Two entropic finite volume schemes for a Nernst--Planck--Poisson system with ion volume constraints, AMaSiS 2021: Applied Mathematics and Simulation for Semiconductors and Electrochemical Systems (Online Event), September 6 - 9, 2021.
-
A. Glitzky, A coarse-grained electrothermal model for organic semiconductor devices (online talk), DMV-ÖMG Jahrestagung 2021 (Online Event), September 27 - October 1, 2021, Universität Passau, September 29, 2021.
-
P. Farrell, Y. Hadjimichael, Ch. Merdon, T. Streckenbach, Toward charge transport in bent nanowires, AMaSiS 2021: Applied Mathematics and Simulation for Semiconductors and Electrochemical Systems (Online Event), September 6 - 9, 2021.
-
M. Kantner, Noise in semiconductor lasers (online talk), MATH+ Spotlight Seminar (Online Event), MATH+, July 14, 2021.
-
M. Liero, Heat and carrier flow in organic semiconductor devices -- Modeling, analysis, and simulation (online talk), AMaSiS 2021: Applied Mathematics and Simulation for Semiconductors and Electrochemical Systems (Online Event), September 6 - 9, 2021, WIAS Berlin, September 6, 2021.
-
M. Heida, Stochastic homogenization in randomly perforated domains (online talk), Annual Workshop of the GAMM Activity Group on Analysis of PDEs (Online Event), September 30 - October 2, 2020, Institute of Science and Technology Austria (IST Austria), Klosterneuburg, October 2, 2020.
-
O. Marquardt, Data-driven electronic structure calculations for semiconductor nanostructures, Efficient Algorithms for Numerical Problems, January 17, 2020, WIAS Berlin, January 17, 2020.
-
O. Marquardt, Electronic properties of semiconductor heterostructures using SPHInX (online tutorial), NUSOD 2020: 20th International Conference on Numerical Simulation of Optoelectronic Devices (Online Event), September 14 - 25, 2020, Politecnico di Torino, September 14, 2020.
-
O. Marquardt, Th. Koprucki, A. Mielke, DESCANT -- Data-driven electronic structure calculations for semiconductor nanostructures, MATH+ Day 2020 (Online Event), Berlin, November 6, 2020.
-
O. Marquardt, Modelling the electronic properties of semiconductor nanowire heterostructures (online talk), Institutsseminar des PDI, Paul-Drude-Institut für Festkörperelektronik, August 23, 2021.
-
O. Marquardt, Semiconductor nanostructures (online talk), IKZ-WIAS Workshop (Online Event), October 30, 2020, WIAS Berlin, IKZ Berlin, October 30, 2020.
-
G. Nika, An existence result for a class of electrothermal drift-diffusion models with Fermi--Gauss statistics for organic semiconductors, Joint Mathematics Meeting, January 15 - 18, 2020, American Mathematical Society/ Mathematical Association of America, Denver, USA, January 15, 2020.
-
N. Dropka , P. Farrell, S. Kayser, N. Rotundo, Numerics for innovative semiconductor devices -- An outlook, German Conference on Crystal Growth, Munich, March 11 - 13, 2020.
-
A. Glitzky, A hybrid model for the electrothermal behaviour of semiconductor devices (online talk), Annual Workshop of the GAMM Activity Group on Analysis of PDEs (Online Event), September 30 - October 2, 2020, Institute of Science and Technology Austria (IST Austria), Klosterneuburg, October 1, 2020.
-
P. Farrell, D. Peschka, Challenges in drift-diffusion semiconductor simulations, Finite Volumes for Complex Applications IX (Online Event), Bergen, Norway, June 15 - 19, 2020.
-
J. Fuhrmann, C. Guhlke, M. Landstorfer, A. Linke, Ch. Merdon, R. Müller, Quality preserving numerical methods for electroosmotic flow, Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Kick-off Conference (Online Event), October 26 - 30, 2020.
-
M. Kantner, Non-isothermal Scharfetter--Gummel scheme for electro-thermal transport simulation in degenerate semiconductors, Finite Volumes for Complex Applications IX (Online Event), June 15 - 19, 2020, University of Bergen, Bergen, Norway, June 16, 2020, DOI 10.1007/978-3-030-43651-3_14 .
-
M. Kantner, Non-isothermal Scharfetter--Gummel scheme for electro-thermal transport simulation in degenerate semiconductors (online talk), Finite Volumes for Complex Applications IX (Online Event), June 15 - 19, 2020, NORCE - Norwegian Research Centre, Bergen, Norway, June 16, 2020.
-
TH. Koprucki, K. Tabelow, T. Streckenbach, T. Niermann, A. Maltsi, Model-based geometry reconstruction of TEM images, MATH+ Day 2020 (Online Event), Berlin, November 6, 2020.
-
M. Liero, Drift-diffusion simulation of S-shaped current-voltage relations for organic semiconductor devices (online talk), SimOEP 2020: International Conference on Simulation of Organic Electronics and Photovoltaics (Online Event), August 31 - September 2, 2020, Zürcher Hochschule für Angewandte Wissenschaften, Switzerland, September 1, 2020.
-
A. Maltsi, Th. Koprucki, T. Streckenbach, K. Tabelow, J. Polzehl, Model-based geometry reconstruction of quantum dots from TEM, Microscopy Conference 2019, Poster session IM 4, Berlin, September 1 - 5, 2019.
-
A. Maltsi, Th. Koprucki, T. Streckenbach, K. Tabelow, J. Polzehl, Model-based geometry reconstruction of quantum dots from TEM, BMS Summer School 2019: Mathematics of Deep Learning, Berlin, August 19 - 30, 2019.
-
A. Maltsi, Model-based geometry reconstruction in TEM images, Sondierungsworkshop MPIE/WIAS ``Elektrochemie, Halbleiternanostrukturen und Metalle", October 14 - 15, 2019, Max-Planck-Institut für Eisenforschung GmbH Düsseldorf, October 15, 2019.
-
A. Maltsi, Model-based geometry reconstruction in TEM images, Sondierungsworkshop MPIE/WIAS ``Elektrochemie, Halbleiternanostrukturen und Metalle", October 14 - November 15, 2019, Max-Planck-Institut für Eisenforschung GmbH Düsseldorf, October 15, 2019.
-
A. Maltsi, Towards model-based geometry reconstruction of quantum dots from TEM, ``9th International Congress on Industrial and Applied Mathematics" (ICIAM 2019), July 15 - 19, 2019, Universitat de València, Spain, July 19, 2019.
-
M. Heida, What is... SQRA discretization of the Fokker--Planck equation?, CRC1114 Colloquium, Freie Universität Berlin, SFB 1114, April 25, 2019.
-
M. Kantner, A generalized Scharfetter--Gummel scheme for degenerate and non-isothermal semiconductors, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), July 8 - 12, 2019, University of Ottawa, Canada, July 8, 2019.
-
M. Kantner, Device-scale simulation of quantum light emitting diodes, International Symposium ,,Semiconductor Nanophotonics'', November 4 - 5, 2019, Technische Universität Berlin, November 4, 2019.
-
M. Kantner, Hybrid modeling of quantum light emitting diodes: Self-consistent coupling of drift-diffusion, Schrödinger--Poisson, and quantum master equations, SPIE Photonics West, February 5 - 7, 2019, San Francisco, USA, February 6, 2019, DOI 10.1117/12.2515209 .
-
M. Kantner, Simulation of quantum light sources using the self-consistently coupled Schrödinger--Poisson-Drift-Diffusion-Lindblad system, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), July 8 - 12, 2019, University of Ottawa, Canada, July 8, 2019.
-
O. Marquardt, Charge confining mechanisms in III-V semiconductor nanowires, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2019), July 8 - 12, 2019, University of Ottawa, Canada, July 8, 2019.
-
O. Marquardt, Data-driven electronic structure calculations for nanostructures (DESCANT), Sondierungsworkshop MPIE/WIAS ``Elektrochemie, Halbleiternanostrukturen und Metalle", October 14 - 15, 2019, Max-Planck-Institut für Eisenforschung GmbH Düsseldorf, October 15, 2019.
-
O. Marquardt, Modelling the electronic properties of semiconductor nanowires, Engineering Physics Seminar, McMaster University, Hamilton, Canada, July 12, 2019.
-
D. Peschka, ``Numerical methods for charge transport in semiconductors: FEM vs FV", 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
A. Glitzky, An existence result for a class of electrothermal drift-diffusion models with Gauss--Fermi statistics for organic semiconductors, ``Partial Differential Equations in Fluids and Solids" (PDE2019), September 9 - 13, 2019, WIAS Berlin, September 12, 2019.
-
A. Glitzky, Drift-diffusion problems with Gauss--Fermi statistics and field-dependent mobility for organic semiconductor devices, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Universität Wien, Technische Universität Wien, Austria, February 22, 2019.
-
TH. Koprucki, Datenmanagement - Forschungsdaten in Modellierung und Simulation, Block-Seminar des SFB 787 ``Nanophotonik'', May 6 - 8, 2019, Technische Universität Berlin, Graal-Müritz, May 6, 2019.
-
TH. Koprucki, Multi-dimensional modeling and simulation of semiconductor devices, Physikalisches Kolloquium, Technische Universität Chemnitz, Institut für Physik, November 27, 2019.
-
TH. Koprucki, On a database of simulated TEM images for In(Ga)As/GaAs quantum dots with various shapes, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2019) , Session ``Nano-structures", July 8 - 12, 2019, University of Ottawa, Canada, July 8, 2019.
-
TH. Koprucki, Towards multiscale modeling of III-N-based LEDs, 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2019) , Session ``Postdeadline Session and Outlook", July 8 - 12, 2019, University of Ottawa, Canada, July 12, 2019.
-
A. Mielke, Thermodynamical modeling via GENERIC: From quantum mechanics to semiconductor devices, Institute of Thermomechanics's Seminar, Czech Academy of Sciences, Prague, March 21, 2019.
-
A. Maltsi, Th. Koprucki, T. Niermann, T. Streckenbach, K. Tabelow, J. Polzehl, Computing TEM images of semiconductor nanostructures, Applied Mathematics and Simulation for Semiconductors (AMaSiS 2018), WIAS Berlin, October 8 - 10, 2018.
-
A. Maltsi, Model-based geometry reconstruction of quantum dots from TEM, DPG-Frühjahrstagung der Sektion Kondensierte Materie (SKM), Fachverband Kristalline Festkörper und deren Mikrostruktur, March 12 - 16, 2018, Technische Universität Berlin, March 12, 2018.
-
N. Rotundo, Consistent modeling of optoelectronic semiconductors via gradient structures, Congress of the Italian Society of Applied and Industrial Mathematics (SIMAI), Minisymposium MS-23 ``Mathematical Modeling of Charge Transport in Low Dimensional Structures (Part II)'', July 2 - 6, 2018, Sapienza Università di Roma, Faculty of Civil and Industrial Engineering, Cosenza, Italy, July 3, 2018.
-
N. Rotundo, On a thermodynamically consistent coupling of quantum system and device equations, The 20th European Conference on Mathematics for Industry (ECMI 2018), Minisymposium ``Mathematical Modeling of Charge Transport in Graphene and Low Dimensional Structures'', August 18 - June 22, 2018, Budapest, Hungary, June 19, 2018.
-
D.H. Doan, J. Fuhrmann, A. Glitzky, Th. Koprucki, M. Liero, On van Roosbroeck systems with Gauss--Fermi statistics, Applied Mathematics and Simulation for Semiconductors (AMaSiS 2018), WIAS Berlin, October 8 - 10, 2018.
-
M. Kantner, M. Mittnenzweig, Th. Koprucki, A hybrid quantum-classical modeling approach for electrically driven quantum dot devices, SPIE Photonics West 2018: Physics and Simulation of Optoelectronic Devices XXVI, January 29 - February 1, 2018, The Moscone Center, San Francisco, USA, January 29, 2018.
-
M. Kantner, Hybrid quantum-classical modeling of quantum dot based single-photon emitting diodes, Workshop Applied Mathematics and Simulation for Semiconductors, WIAS Berlin, October 10, 2018.
-
M. Kantner, Modeling and simulation of electrically driven quantum light emitters, Leibniz MMS Days, Leibniz Institut für Oberflächenmodifizierung (IOM), Leipzig, March 2, 2018.
-
M. Kantner, Thermodynamically consistent modeling of electrically driven quantum dot based light emitters on a device scale, Workshop ,,Nonlinear Dynamics in Semiconductor Lasers (NDSL2018)'', June 18 - 20, 2018, WIAS, Berlin, June 18, 2018.
-
D. Peschka, Steering pattern formation during dewetting with interface and contact lines properties, The 20th European Conference on Mathematics for Industry (ECMI 2018), Minisymposium 38 ``ECMI Special Interest Group: Material Design and Performance in Sustainable Energies'', June 18 - 22, 2018, Budapest, Hungary, June 21, 2018.
-
C. Cancès, C. Chainais-Hillairet, J. Fuhrmann, B. Gaudeul, Numerical schemes for a reduced case of an improved Nernst--Planck--Poisson model, Applied Mathematics and Simulation for Semiconductors (AMaSiS 2018), WIAS Berlin, October 8 - 10, 2018.
-
A. Glitzky, Electrothermal feedback in organic LEDs, Workshop ``Numerical Optimization of the PEM Fuel Cell Bipolar Plate'', March 20, 2018, Zentrum für Solarenergie- und Wasserstoff-Forschung (ZSW), Ulm, March 20, 2018.
-
M. Thomas, Optimization of the radiative emission for mechanically strained optoelectronic semiconductor devices, 9th International Conference ``Inverse Problems: Modeling and Simulation'' (IPMS 2018), Minisymposium M16 ``Inverse and Control Problems in Mechanics'', May 21 - 25, 2018, The Eurasian Association on Inverse Problems, Malta, May 24, 2018.
-
TH. Koprucki, Highly accurate discretizations for non-Boltzmann charge transport in semiconductors, 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), Session ``Numerical Methods'', November 5 - 9, 2018, The University of Hong Kong, China, November 6, 2018.
-
TH. Koprucki, Model pathway diagrams for the representation of mathematical models, The Leibniz ``Mathematical Modeling and Simulation'' Days 2018, February 28 - March 2, 2018, Leibniz Institute for Surface Engineering (IOM) & Leibniz-Institut für Troposphärenforschung (TROPOS), Leipzig, February 28, 2018, DOI 10.5446/35360 .
-
TH. Koprucki, Multi-dimensional modeling und simulation of nanophotonic devices, Block-Seminar des SFB 787 ``Nanophotonik'', May 7 - 9, 2018, Technische Universität Berlin, Graal-Müritz, May 9, 2018.
-
TH. Koprucki, Numerical methods for drift-diffusion equations, sc Matheon 11th Annual Meeting ``Photonic Devices'', February 8 - 9, 2018, Konrad-Zuse-Zentrum für Informationstechnik Berlin, February 8, 2018.
-
TH. Koprucki, Towards model-based geometry reconstruction of quantum dots from TEM, 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), Session ``Nanostructures'', November 5 - 9, 2018, The University of Hong Kong, China, November 8, 2018.
-
M. Liero, Feel the heat---Modeling of electrothermal feedback in organic devices, A Joint Meeting of the Society for Natural Philosophy and the International Society for the Interaction of Mathematics and Mechanics ``Mathematics & Mechanics: Natural Philosophy in the 21st Century'', June 24 - 27, 2018, University of Oxford, Mathematical Institute, UK, June 25, 2018.
-
O. Marquardt, Computational design of core-shell nanowire crystal-phase quantum rings for the observation of Aharonov--Bohm oscillations, The Leibniz ``Mathematical Modeling and Simulation'' Days 2018, February 28 - March 2, 2018, Leibniz Institute for Surface Engineering (IOM) & Leibniz-Institut für Troposphärenforschung (TROPOS), Leipzig, March 1, 2018.
-
O. Marquardt, Computational design of core-shell nanowire crystal-phase quantum rings for the observation of Aharonov--Bohm oscillations, 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018) , Session " Nanostructures", November 5 - 9, 2018, The University of Hong Kong, China, November 6, 2018.
-
O. Marquardt, Data-driven electronic structure calculations for nanostructures, Applied Mathematics and Simulation for Semiconductors (AMaSiS 2018), October 8 - 10, 2018, WIAS, October 10, 2018.
-
O. Marquardt, Data-driven electronic structure calculations in semiconductor nanostructures --- Beyond the eight-band k&cdot&p formalism, 18th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2018), Session ``Numerical Methods'', November 5 - 9, 2018, The University of Hong Kong, China, November 6, 2018.
-
O. Marquardt, Modelling the electronic properties of polytype heterostructure (synopsis), QuantumWise A/S, Kgs. Lyngby, Denmark, August 21, 2018.
-
O. Marquardt, Observation of Aharonov--Bohm oscillations in core-shell nanowire crystal-phase quantum rings, DPG-Frühjahrstagung der Sektion Kondensierte Materie (SKM), Fachverband Halbleiterphysik, March 12 - 16, 2018, Technische Universität Berlin, March 13, 2018.
-
A. Mielke, Entropy and gradient structures for quantum Markov semigroups and couplings to macroscopic thermodynamical systems, Nonlinear Mechanics Seminar, University of Bath, Mathematical Sciences, UK, May 22, 2018.
-
M. Kantner, Hybrid quantum-classical modeling of electrically driven quantum light sources, Meeting of the MATHEON Scientific Advisory Board 2017, TU Berlin, Institut für Mathematik, November 13, 2017.
-
M. Kantner, Simulations of quantum dot devices by coupling of quantum master equations and semi-classical transport theory, 17th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD2017), July 24 - 28, 2017, Technical University of Denmark, Copenhagen, July 27, 2017.
-
M. Liero, Modeling and simulation of electrothermal feedback in large-area organic LEDs, Numerical Simulation of Optoelectronic Devices (NUSOD 2017), session ``Light-Emitting Diodes'', July 24 - 28, 2017, Technical University of Denmark, Lyngby Campus, Kopenhagen, Denmark, July 25, 2017.
-
D. Peschka, Doping optimization for optoelectronic devices, Numerical Simulation of Optoelectronic Devices (NUSOD 2017), Post-Deadline session, July 27 - 28, 2017, Technical University, Lyngby Campus, Kopenhagen, Denmark, July 28, 2017.
-
A. Fischer, M. Liero, A. Glitzky, Th. Koprucki, K. Vandewal, S. Lenk, S. Reinicke, Predicting electrothermal behavior from lab-size OLEDs to large area lighting panels, MRS Spring Meeting & Exhibit, Materials Research Society, Phoenix, Arizona, USA, April 17 - 21, 2017.
-
A. Glitzky, Electrothermal description of organic semiconductor devices by $p(x)$-Laplace thermistor models, 88th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2017), Section S14 ``Applied Analysis'', March 6 - 10, 2017, Bauhaus Universität Weimar/Technische Universität Ilmenau, Weimar, March 9, 2017.
-
M. Thomas, Mathematical modeling and analysis of evolution processes in solids and the influence of bulk-interface-interaction, Humboldt-Universität zu Berlin, Institut für Mathematik, October 20, 2017.
-
TH. Koprucki, Comparison of consistent flux discretizations for drift diffusion beyond Boltzmann statistics, Numerical Simulation of Optoelectronic Devices (NUSOD 2017), session ``Numerical Methods'', July 24 - 28, 2017, Technical University of Denmark, Lyngby Campus, Kopenhagen, Denmark, July 27, 2017.
-
TH. Koprucki, Halbleiter-Bauteilsimulation: Modelle und numerische Verfahren, Block-Seminar des SFB 787 ``Nanophotonik'', June 7 - 9, 2017, Technische Universität Berlin, Graal-Müritz, June 8, 2017.
-
TH. Koprucki, Mathematical knowledge management as a route to sustainability in mathematical modeling and simulation, 2nd Leibniz MMS Days 2017, February 22 - 24, 2017, Technische Informationsbibliothek (TIB), Hannover, February 22, 2017, DOI 10.5446/21908 .
-
TH. Koprucki, Mathematical models as research data in numerical simulation of opto-electronic devices, Numerical Simulation of Optoelectronic Devices (NUSOD 2017), session ``Model Representation'', July 24 - 28, 2017, Technical University of Denmark, Lyngby Campus, Kopenhagen, Denmark, July 27, 2017.
-
TH. Koprucki, On current injection into single quantum dots through oxide-confined pn-diodes, 10th Annual Meeting ``Photonic Devices'', February 9 - 10, 2017, Zuse Institute Berlin (ZIB), Berlin, February 9, 2017.
-
TH. Koprucki, On the Scharfetter--Gummel scheme for the discretization of drift-diffusion equations and its generalization beyond Boltzmann, Kolloquium Modellierung, Numerik, Differentialgleichungen, Technische Universität Berlin, Institut für Mathematik, May 30, 2017.
-
M. Liero, A. Glitzky, Th. Koprucki, J. Fuhrmann, 3D electrothermal simulations of organic LEDs showing negative differential resistance, Multiscale Modelling of Organic Semiconductors: From Elementary Processes to Devices, Grenoble, France, September 12 - 15, 2017.
-
A. Mielke, Mathematical modeling of semiconductors: From quantum mechanics to devices, CIM-WIAS Workshop ``Topics in Applied Analysis and Optimisation'', December 6 - 8, 2017, Centro de Matemática, Lisboa, Portugal, December 8, 2017.
-
M. Mittnenzweig, A variational approach to quantum master equations coupled to a semiconductor PDE, Workshop ``Variational Methods for Evolution'', November 12 - 17, 2017, Mathematisches Forschungsinstitut Oberwolfach, November 14, 2017.
-
M. Mittnenzweig, Variational methods for quantum master equations, BMS -- BGSMath Junior Meeting, October 9 - 10, 2017, Berlin Mathematical School and Barcelona Graduate School of Mathematics, Barcelona, Spain, October 10, 2017.
-
N. Rotundo, Numerical methods for drift-diffusion models, Seminar ``Angewandte Mathematik'', Ernst Moritz Arndt Universität Greifswald, Institut für Mathematik und Informatik, June 28, 2016.
-
N. Rotundo, On some extension of energy-drift-diffusion models, The 19th European Conference on Mathematics for Industry (ECMI 2016), Minisymposium 34 ``Mathematical Modeling of Charge Transport in Graphene and Low Dimensional Structure'', June 13 - 18, 2016, Universidade de Santiago de Compostela, Spain, June 14, 2016.
-
N. Rotundo, Thermodynamic modeling of optoelectronic semiconductor devices, Mathematical Models for Quantum and Classical Mechanics (SEMODAY2016), November 17 - 18, 2016, Università degli Studi di Firenze, Dipartamento di Matematica, Florence, Italy, November 18, 2016.
-
M. Kantner, Multi-scale modeling and numerical simulation of single-photon emitters, Matheon Workshop--9th Annual Meeting ``Photonic Devices", Zuse Institut, Berlin, March 3, 2016.
-
M. Kantner, Multi-scale modelling and simulation of single-photon sources on a device level, Euro--TMCS II Theory, Modelling & Computational Methods for Semiconductors, Tyndall National Institute and University College Cork, Cork, Ireland, December 9, 2016.
-
M. Liero, OLEDs - a hot matter? Electrothermal modeling of OLEDs., sc Matheon Workshop, 9th Annual Meeting ``Photonic Devices'', March 3 - 4, 2016, Zuse Institute Berlin, Berlin, March 4, 2016.
-
M. Liero, On $p(x)$-Laplace thermistor models describing eletrothermal feedback in organic semiconductors, The 19th European Conference on Mathematics for Industry (ECMI 2016), Minisymposium 23 ``Charge Transport in Semiconductor Materials: Emerging and Established Mathematical Topics'', June 13 - 17, 2016, Universidade de Santiago de Compostela, Spain, June 15, 2016.
-
M. Liero, On $p(x)$-Laplace thermistor models describing eletrothermal feedback in organic semiconductors, Joint Annual Meeting of DMV and GAMM, Section 14 ``Applied Analysis'', March 7 - 11, 2016, Technische Universität Braunschweig, Braunschweig, March 9, 2016.
-
M. Liero, On electrothermal feedback in organic light-emitting diodes, Berlin Dresden Prague Würzburg Workshop ``Mathematics of Continuum Mechanics'', Technische Universität Dresden, Fachbereich Mathematik, December 5, 2016.
-
M. Mittnenzweig, Gradient structures for Lindblad equations satisfying detailed balance, 3rd PhD Workshop, May 30 - 31, 2016, International Research Training Group of the Collaborative Research Center (SFB) 1114 ``Scaling Cascades in Complex Systems'', Güstrow, May 31, 2016.
-
D. Peschka, Towards the optimization of Ge micro bridges, The 19th European Conference on Mathematics for Industry (ECMI 2016), minisymposium ``Charge Transport in Semiconductor Materials: Emerging and Established Mathematical Topics'', June 13 - 17, 2016, Universidade de Santiago de Compostela, Faculty of Mathematics, Santiago de Compostela, Spain, June 15, 2016.
-
D. Peschka, Towards the optimization of on-chip germanium lasers, sc Matheon Workshop, 9th Annual Meeting ``Photonic Devices'', March 3 - 4, 2016, Zuse Institute Berlin, Berlin, March 4, 2016.
-
A. Glitzky, $p(x)$-Laplace thermistor models for electrothermal effects in organic semiconductor devices, 7th European Congress of Mathematics (7ECM), Minisymposium 22 ``Mathematical Methods for Semiconductors'', July 18 - 22, 2016, Technische Universität Berlin, July 22, 2016.
-
A. Glitzky, $p(x)$-Laplace thermistor models for electrothermal feedback in organic semiconductor devices, 9th European Conference on Elliptic and Parabolic Problems, May 23 - 27, 2016, University of Zurich, Institute of Mathematics, Gaeta, Italy, May 23, 2016.
-
M. Thomas, Analysis and optimization for edge-emitting semiconductor heterostructures, 7th European Congress of Mathematics (ECM), session CS-8-A, July 18 - 22, 2016, Technische Universität Berlin, Berlin, July 19, 2016.
-
M. Thomas, Analysis and optimization for edge-emitting semiconductor heterostructures, The 11th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 2 ``Emergence and Dynamics of Patterns in Nonlinear Partial Differential Equation'', July 1 - 5, 2016, The American Institute of Mathematical Sciences, Orlando (Florida), USA, July 3, 2016.
-
M. Thomas, Mathematische Modellierung, Analysis und Optimierung von Germanium-Lasern, Vortrag vor dem WGL-Präsidenten anlässlich seines WIAS-Besuchs, WIAS Berlin, Berlin, February 18, 2016.
-
D.H. Doan, Numerical methods in non-Boltzmann regimes, sc Matheon Workshop, 9th Annual Meeting ``Photonic Devices'', March 3 - 4, 2016, Zuse Institute Berlin, Berlin, March 4, 2016.
-
P. Farrell, Scharfetter--Gummel schemes for Non-Boltzmann statistics, Conference on Scientific Computing (ALGORITMY 2016), March 14 - 18, 2016, Slovak University of Technology, Department of Mathematics and Descriptive Geometry, Podbanské, Slovakia, March 17, 2016.
-
P. Farrell, Scharfetter--Gummel schemes for non-Boltzmann statistics, The 19th European Conference on Mathematics for Industry (ECMI2016), Minisymposium 23 ``Charge Transport in Semiconductor Materials: Emerging and Established Mathematical Topics'', June 13 - 17, 2016, Universidade de Santiago de Compostela, Spain, June 14, 2016.
-
TH. Koprucki, On current injection into single quantum dots through oxide-confined PN-diodes, 16th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2016), July 7 - 17, 2016, University of Sydney, Sydney, Australia, July 14, 2016.
-
E. Cinti, Quantitative flatness results for nonlocal minimal surfaces in low dimensions, Theory of Applications of Partial Differential Equations (PDE 2015), November 30 - December 4, 2015, WIAS Berlin, Berlin, December 2, 2015.
-
N. Rotundo, Analytical methods for doping optimization for semiconductor devices, Minisymposium ``Numerical and Analytical Aspects in Semiconductor Theory'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 10, 2015.
-
N. Rotundo, Towards doping optimization of semiconductor lasers, 24th International Conference on Transport Theory, September 7 - 11, 2015, University of Catania, Taormina, Italy, September 9, 2015.
-
M. Kantner, Multi-scale modeling and simulation of electrically pumped single-photon sources, International Nano-Optoelectronics Workshop (iNOW 2015), Tokio, Japan, August 3 - 7, 2015.
-
TH. Koprucki, On device concepts for CMOS-compatible edge-emitters based on strained germanium, Symposium ``Alternative Semiconductor Integration in Si Microelectronics: Materials, Techniques and Applications'' of the E-MRS Fall Meeting 2015, September 15 - 18, 2015, Warsaw University of Technology, Krakow, Poland, September 18, 2015.
-
TH. Koprucki, On device concepts for CMOS-compatible edge-emitters based on strained germanium, 15th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2015), September 7 - 11, 2015, National Taiwan University, Taipeh, Taiwan, Province Of China, September 8, 2015.
-
M. Liero, Electrothermal modeling of large-area OLEDs, sc Matheon Center Days, April 20 - 21, 2015, Technische Universität Berlin, Institut für Mathematik, Berlin, April 20, 2015.
-
M. Liero, OLEDs -- eine heiße Sache?, Organische Leuchtdioden, Workshop im Handlungsfeld Lichttechnik, OpTec Berlin Brandenburg e.V., Berlin, May 18, 2015.
-
M. Liero, On $p(x)$-Laplace thermistor models describing electrothermal feedback in organic semiconductor devices, Theory of Applications of Partial Differential Equations (PDE 2015), November 30 - December 4, 2015, WIAS Berlin, Berlin, December 3, 2015.
-
M. Liero, On a PDE thermistor system for large-area OLEDs, Applied Mathematics and Simulation for Semiconductors (AMaSiS 2015), March 11 - 13, 2015, WIAS Berlin, Berlin, March 12, 2015.
-
D. Peschka, Mathematical modeling, analysis, and optimization of strained germanium-microbridges, sc Matheon Center Days, April 20 - 21, 2015, Technische Universität Berlin, Institut für Mathematik, Berlin, April 20, 2015.
-
A. Glitzky, Analysis of $p(x)$-Laplace thermistor models for electrothermal feedback in organic semiconductor devices, 3rd Workshop of the GAMM Activity Group ``Analysis of Partial Differential Equations'', September 30 - October 2, 2015, Universität Kassel, Institut für Mathematik, Kassel, September 30, 2015.
-
M. Thomas, Analysis for edge-emitting semiconductor heterostructures, Minisymposium ``Numerical and Analytical Aspects in Semiconductor Theory'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 10, 2015.
-
M. Thomas, Modeling of edge-emitting lasers based on tensile strained germanium microstripes, Applied Mathematics and Simulation for Semiconductors (AMaSiS 2015), March 11 - 13, 2015, WIAS Berlin, Berlin, March 11, 2015.
-
D.H. Doan, On modifications of the Scharfetter--Gummel scheme for drift-diffusion equations with Fermi-like distribution functions, Kick-Off Meeting of the ECMI Special Interest Group ``Sustainable Energy'' on Nanostructures for Photovoltaics and Energy Storage, December 8 - 9, 2014, Technische Universität Berlin, Institut für Mathematik, December 8, 2014.
-
TH. Koprucki, DeviceSimulation: Mathematische Fragestellungen und Numerik, Block-Seminar des SFB 787 ``Nanophotonik'', May 21 - 23, 2014, Technische Universität Berlin, Graal-Müritz, May 23, 2014.
-
TH. Koprucki, On modifications of the Scharfetter--Gummel scheme for drift-diffusion equations with Fermi-like statistical distribution functions, 14th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2014), September 1 - 5, 2014, Palma de Mallorca, Spain, September 3, 2014.
-
M. Liero, Electrothermical modeling of large-area OLEDs, Kick-Off Meeting of the ECMI Special Interest Group ``Sustainable Energy'' on Nanostructures for Photovoltaics and Energy Storage, December 8 - 9, 2014, Technische Universität Berlin, Institut für Mathematik, December 8, 2014.
-
A. Glitzky, Drift-diffusion models for heterostructures in photovoltaics, 8th European Conference on Elliptic and Parabolic Problems, Minisymposium ``Qualitative Properties of Nonlinear Elliptic and Parabolic Equations'', May 26 - 30, 2014, Universität Zürich, Institut für Mathematik, organized in Gaeta, Italy, May 27, 2014.
-
H. Neidhardt, Landauer--Bütikker formula applied to photon emitting and absorbing system, Workshop ``Mathematical Challenge of Quantum Transport in Nanosystems'' (Pierre Duclos Workshop), September 23 - 26, 2014, Saint Petersburg National Research University of Informational Technologies, Mechanics, and Optics, Russian Federation, September 24, 2014.
-
TH. Koprucki, Generalization of the Scharfetter--Gummel scheme, Organic Photovoltaics Workshop 2013, December 10 - 11, 2013, University of Oxford, Mathematical Insitute, UK, December 10, 2013.
-
TH. Koprucki, Selbstaufheizungs-Effekte in Halbleitern, negativer differentieller Widerstand und Bistabilität, Doktorandenseminar des SFB 787 Nanophotonik, Technische Universität Berlin, Institut für Physik, November 29, 2013.
-
TH. Koprucki, Discretization scheme for drift-diffusion equations with a generalized Einstein relation, scshape Matheon Workshop ``6th Annual Meeting Photonic Devices'', February 21 - 22, 2013, Konrad-Zuse-Zentrum für Informationstechnik Berlin, February 22, 2013.
-
M. Liero, Gradient structures and geodesic convexity for reaction-diffusion system, SIAM Conference on Mathematical Aspects of Materials Science (MS13), Minisymposium ``Material Modelling and Gradient Flows'' (MS100), June 9 - 12, 2013, Philadelphia, USA, June 12, 2013.
-
M. Liero, On gradient structures and geodesic convexity for reaction-diffusion systems, Research Seminar, Westfälische Wilhelms-Universität Münster, Institut für Numerische und Angewandte Mathematik, April 17, 2013.
-
A. Glitzky, Nonlinear electrothermal feedback in organic semiconductors, Organic Photovoltaics Workshop 2013, December 10 - 11, 2013, University of Oxford, Mathematical Insitute, UK, December 10, 2013.
-
A. Glitzky, Electro-thermal modeling of organic semiconductors describing negative differential resistance induced by self-heating, 13th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD 2013), August 19 - 22, 2013, Vancouver, Canada, August 20, 2013.
-
M. Thomas, Mathematical modeling, analysis and optimization of strained germanium microbridges, sc Matheon Center Days, Technische Universität Berlin, November 5, 2013.
-
A. Mielke, Analysis, modeling, and simulation of semiconductor devices, Kolloquium Simulation Technology, Universität Stuttgart, SRC Simulation Technology, May 14, 2013.
-
A. Mielke, Mathematische und thermodynamische Modellierung von Halbleiterstrukturen, Block-Seminar des SFB 787 ``Nanophotonik'', May 6 - 8, 2013, Technische Universität Berlin, Graal-Müritz, May 8, 2013.
-
A. Mielke, Thermodynamic modeling of the Maxwell--Bloch and the semiconductor equations via GENERIC, Modeling, Analysis and Simulation of Optical Modes in Photonic Devices (MASOMO 13), April 10 - 12, 2013, WIAS Berlin, April 10, 2013.
-
TH. Koprucki, A. Glitzky, A. Fischer, Electronic and thermal effects in organic semiconductors, Organic Photovoltaics Workshop, Oxford University, Mathematical Institute, UK, April 2, 2012.
-
TH. Koprucki, K. Gärtner, A. Wilms, U. Bandelow, A. Mielke, Multidimensional modeling and simulation of quantum-dot lasers, Fachtagung Leibniz-Nano (1. Nanotechnologie-Workshop der Leibniz-Gemeinschaft), Berlin, January 30 - 31, 2012.
-
TH. Koprucki, Discretization scheme for drift-diffusion equations with strong diffusion enhancement, 12th International Conference on Numerical Simulation of Optoelectronic Devices NUSOD'12, August 28 - 31, 2012, Chinese Academy of Science, Shanghai Institute for Technical Physics, August 29, 2012.
-
TH. Koprucki, On coupling of optical models with electronic models for simulation of quantum-dot VCSELs, 5th Annual Meeting Photonic Devices, February 23 - 24, 2012, Konrad-Zuse-Zentrum für Informationstechnik, Berlin, February 24, 2012.
-
TH. Koprucki, Semi-classical modeling of quantum dot lasers with microscopic treatment of Coulomb scattering, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 24, 2012.
-
M. Liero, Interfaces in reaction-diffusion systems, Seminar ``Dünne Schichten'', Technische Universität Berlin, Institut für Mathematik, February 9, 2012.
-
M. Liero, Interfaces in solar cells, 5th Annual Meeting Photonic Devices, February 23, 2012, Konrad-Zuse-Zentrum für Informationstechnik, Berlin, February 24, 2012.
-
M. Liero, WIAS-TeSCA simulations in photovoltaics for a point contact concept of heterojunction thin film solar cells, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 25, 2012.
-
A. Glitzky, An electronic model for solar cells taking into account active interfaces, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 27, 2012.
-
A. Glitzky, Mathematische Modellierung und Simulation organischer Halbleiterbauelemente, Senatsausschuss Wettbewerb (SAW), Sektion D der Leibniz-Gemeinschaft, Leibniz-Institut für Analytische Wissenschaften (ISAS), Dortmund, September 14, 2012.
-
K. Gärtner, A. Glitzky, Mathematics and simulation of the charge transport in semiconductor sensors, Fachtagung Leibniz-Nano (1. Nanotechnologie-Workshop der Leibniz-Gemeinschaft), Berlin, January 30 - 31, 2012.
-
A. Mielke, Multidimensional modeling and simulation of optoelectronic devices, Challenge Workshop ``Modeling, Simulation and Optimisation Tools'', September 24 - 26, 2012, Technische Universität Berlin, September 24, 2012.
-
A. Mielke, Using gradient structures for modeling semiconductors, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 24, 2012.
-
H. Neidhardt, On the abstract Landauer--Buettiker formula and applications, Workshop on Spectral Theory and Differential Operators, August 27 - 31, 2012, Technische Universität Graz, Institut für Numerische Mathematik, Austria, August 30, 2012.
-
P.N. Racec, H. Neidhardt, H.-Chr. Kaiser, R. Racec, Electronic quantum transport in semiconductor nanostructures, Fachtagung Leibniz-Nano (1. Nanotechnologie-Workshop der Leibniz-Gemeinschaft), Berlin, January 30 - 31, 2012.
-
P.N. Racec, Finite volume discretization and R-matrix formalism for cylindrical nanowire heterostructures, Seminar Laboratory 30 ``Nanoscale Condensed Matter Laboratory'', National Institute of Materials Physics, Bucharest, Romania, October 9, 2012.
-
P.N. Racec, Quantum transport and the R-matrix formalism for cylindrical nanowire heterostructures, Technische Universität Graz, Institut für Theoretische Physik, Austria, September 13, 2012.
-
P.N. Racec, Quantum transport in cylindrical nanowires with constrictions, 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Mini-Symposium ``Scattering problems for quantum, electromagnetic, and acoustic waveguides'', September 10 - 14, 2012, Universität Wien, Austria, September 10, 2012.
-
P.N. Racec, Quantum transport in semiconductor nano-heterostructures, International Workshop ``Mathematics for Semiconductur Heterostructures: Modeling, Analysis, and Numerics'', September 24 - 28, 2012, WIAS Berlin, September 28, 2012.
-
A. Glitzky, An electronic model for solar cells including active interfaces, Workshop ``Mathematical Modelling of Organic Photovoltaic Devices'', University of Cambridge, Department of Applied Mathematics and Theoretical Physics, UK, June 9, 2011.
-
A. Mielke, Thermodynamical modeling of bulk-interface interaction in reaction-diffusion systems, Interfaces and Discontinuities in Solids, Liquids and Crystals (INDI2011), June 20 - 23, 2011, Gargnano (Brescia), Italy, June 20, 2011.
-
P.N. Racec, R-matrix and finite volume method for cylindrical nanowire heterostructures, Mathematical Challenges of Quantum Transport in Nano-Optoelectronic Systems, February 4 - 5, 2011, WIAS, February 4, 2011.
-
A. Mielke, Mathematical approaches to thermodynamic modeling, Autumn School on Mathematical Principles for and Advances in Continuum Mechanics, November 7 - 12, 2011, Centro di Ricerca Matematica ``Ennio De Giorgi'', Pisa, Italy.
-
TH. Koprucki, Multi-species modeling of quantum dot lasers with microscopic treatment of Coulomb scattering, 10th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD) 2010, September 6 - 9, 2010, Georgia Institute of Technology, Atlanta, USA, September 7, 2010.
-
A. Glitzky, Existence of bounded steady state solutions to spin-polarized drift-diffusion systems, Workshop on Drift Diffusion Systems and Related Problems: Analysis, Algorithms and Computations, WIAS, Research Group ``Numerical Mathematics and Scientific Computing'', March 25, 2010.
-
J.A. Griepentrog, Maximal regularity for nonsmooth parabolic boundary value problems in Sobolev--Morrey spaces, International Conference on Elliptic and Parabolic Equations, November 30 - December 4, 2009, WIAS, December 1, 2009.
-
P.N. Racec, Quantum transport in cylindrical nanowire heterostructures: The scattering problem, Paul-Drude-Institut für Festkörperelektronik, Abteilung Epitaxie, Berlin, May 13, 2009.
-
M. Ehrhardt, A high order finite element method for waves in periodic structures, 9th International Conference on Spectral and High Order Methods (ICOSAHOM09), Minisymposium ``High-order Methods for Linear and Nonlinear Wave Equations'', June 22 - 26, 2009, Norwegian University of Science and Technology, Trondheim, June 24, 2009.
-
K. Gärtner, J.A. Griepentrog, H. Langmach, The van Roosbroeck system, its mathematical properties, and detector simulation examples, 11th European Symposium on Semiconductor Detectors, Wildbad Kreuth, June 7 - 11, 2009.
-
K. Gärtner, Charge explosion studies, 5th Meeting of the Detector Advisory Committee for the European XFEL, April 28 - 29, 2009, European XDAC, Hamburg, April 28, 2009.
-
H.-Chr. Kaiser, Transient Kohn--Sham theory, Jubiläumssymposium ``Licht -- Materialien -- Modelle'' (100 Jahre Innovation aus Adlershof), Berlin-Adlershof, September 7 - 8, 2009.
-
J. Rehberg, Functional analytic properties of the quantum mechanical particle density operator, International Workshop on Quantum Systems and Semiconductor Devices: Analysis, Simulations, Applications, April 20 - 24, 2009, Peking University, School of Mathematical Sciences, Beijing, China, April 21, 2009.
-
P.N. Racec, Modeling of nanowire transistor, May 7 - 14, 2008, National Institute of Materials Physics, Bucharest, Romania, May 8, 2008.
-
A. Glitzky, Analysis of spin-polarized drift-diffusion models, 79th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2008), session ``Applied Analysis'', March 31 - April 4, 2008, University of Bremen, April 1, 2008.
-
H.-Chr. Kaiser, A drift-diffusion model for semiconductors with internal interfaces, Annual Meeting of the Deutsche Mathematiker-Vereinigung 2008, Minisymposium ``Analysis of Reaction-Diffusion Systems with Internal Interfaces'', September 15 - 19, 2008, Friedrich-Alexander-Universität Erlangen-Nürnberg, September 15, 2008.
-
H.-Chr. Kaiser, A thermodynamic approach to transient Kohn--Sham theory, 100th Statistical Mechanics Conference, December 13 - 18, 2008, Rutgers, The State University of New Jersey, New Brunswick, USA, December 16, 2008.
-
H.-Chr. Kaiser, On drift-diffusion Kohn--Sham theory, 79th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2008), session ``Applied Analysis'', March 31 - April 4, 2008, University of Bremen, April 1, 2008.
-
P.N. Racec, Modelling of nanowire transistors in Landauer--Büttiker formalism, Spring Meeting of the Condensed Matter Division of the Deutsche Physikalische Gesellschaft, Berlin, February 25 - 29, 2008.
-
P.N. Racec, Quantum transport in cylindrical nanowire heterostructures, Workshop on Mathematical Aspects of Transport in Mesoscopic Systems, December 4 - 7, 2008, Dublin Institute for Advanced Studies, School of Theoretical Physics, Ireland, December 6, 2008.
-
H.-Chr. Kaiser, A drift-diffusion model of transient Kohn--Sham theory, First Joint International Meeting between the American Mathematical Society and the Polish Mathematical Society, Special Session ``Mathematics of Large Quantum Systems'', July 31 - August 3, 2007, University of Warsaw, Poland, August 3, 2007.
-
J. Rehberg, An elliptic model problem including mixed boundary conditions and material heterogeneities, Fifth Singular Days, April 23 - 27, 2007, International Center for Mathematical Meetings, Luminy, France, April 26, 2007.
-
J. Rehberg, On Schrödinger--Poisson systems, International Conference ``Nonlinear Partial Differential Equations'' (NPDE 2007), September 10 - 15, 2007, Institute of Applied Mathematics and Mechanics of NASU, Yalta, Ukraine, September 13, 2007.
-
J. Rehberg, Operator functions inherit monotonicity, Mini-Workshop on PDE's and Quantum Transport, March 12 - 16, 2007, Aalborg University, Department of Mathematical Sciences, Denmark, March 14, 2007.
-
J. Rehberg, Über Schrödinger-Poisson-Systeme, Chemnitzer Mathematisches Colloquium, Technische Universität Chemnitz, Fakultät für Mathematik, May 24, 2007.
-
F. Schmid, An evolution model in contact mechanics with dry friction, 6th International Congress on Industrial and Applied Mathematics (ICIAM), July 16 - 20, 2007, ETH Zürich, Switzerland, July 19, 2007.
-
K. Gärtner, A. Glitzky, Th. Koprucki, Analysis and simulation of spin-polarized drift-diffusion models, Evaluation Colloquium of the DFG Priority Program SPP 1285 ``Semiconductor Spintronics'', Bad Honnef, December 14 - 15, 2006.
-
A. Glitzky, R. Nürnberg, U. Bandelow, ttfamily WIAS-TeSCA: Simulation of semiconductor lasers, Laser-Optik-Berlin, March 23 - 24, 2006.
-
A. Glitzky, Energy models where the equations are defined on different domains, GAMM Annual Meeting 2006, March 27 - 31, 2006, Technische Universität Berlin, March 29, 2006.
-
J. Rehberg, Existence and uniqueness for van Roosbroeck's system in Lebesque spaces, Conference ``Recent Advances in Nonlinear Partial Differential Equations and Applications'', Toledo, Spain, June 7 - 10, 2006.
-
J. Rehberg, Regularity for nonsmooth elliptic problems, Crimean Autumn Mathematical School, September 20 - 25, 2006, Vernadskiy Tavricheskiy National University, Laspi, Ukraine, September 21, 2006.
-
J. Rehberg, The Schrödinger--Poisson system, Colloquium in Honor of Prof. Demuth, September 10 - 11, 2006, Universität Clausthal, September 10, 2006.
-
A. Glitzky, An application of the Implicit Function Theorem to stationary energy models for semiconductor devices, International Workshop ``Regularity for nonlinear and linear PDEs in nonsmooth domains'', September 4 - 7, 2005, Universität Stuttgart, Hirschegg, Austria, September 5, 2005.
-
A. Glitzky, Stationary energy models for semicoductor devices with incompletely ionized impurities, 2nd Joint Meeting of AMS, DMV, ÖMG, June 16 - 19, 2005, Johannes Gutenberg Universität, Mainz, June 19, 2005.
-
J. Rehberg, Elliptische und parabolische Probleme aus Anwendungen, Kolloquium im Fachbereich Mathematik, Universität Darmstadt, May 18, 2005.
-
J. Rehberg, Existence, uniqeness and regularity for quasilinear parabolic systems, International Conference ``Nonlinear Partial Differential Equations'', September 17 - 24, 2005, Institute of Applied Mathematics and Mechanics Donetsk, Alushta, Ukraine, September 18, 2005.
-
J. Rehberg, H$^1,q$-regularity for linear, elliptic boundary value problems, Regularity for nonlinear and linear PDEs in nonsmooth domains - Analysis, simulation and application, September 5 - 7, 2005, Universität Stuttgart, Deutsche Forschungsgemeinschaft (SFB 404), Hirschegg, Austria, September 6, 2005.
-
J. Rehberg, Regularität für elliptische Probleme mit unglatten Daten, Oberseminar Prof. Escher/Prof. Schrohe, Technische Universität Hannover, December 13, 2005.
-
J. Rehberg, Some analytical ideas concerning the quantum-drift-diffusion systems, Workshop ``Problèmes spectraux non-linéaires et modèles de champs moyens'', April 4 - 8, 2005, Institut Henri Poincaré, Paris, France, April 5, 2005.
-
J. Rehberg, Analysis of macroscopic and quantum mechanical semiconductor models, International Visitor Program ``Nonlinear Parabolic Problems'', August 8 - November 18, 2005, Finnish Mathematical Society (FMS), University of Helsinki, and Helsinki University of Technology, Finland, November 1, 2005.
-
J. Rehberg, Existence, uniqueness and regularity for quasilinear parabolic systems, Conference ``Nonlinear Parabolic Problems'', October 17 - 21, 2005, Finnish Mathematical Society (FMS), University of Helsinki, and Helsinki University of Technology, Finland, October 20, 2005.
-
J. Fuhrmann, H.-Chr. Kaiser, Th. Koprucki, G. Schmidt, Electronic states in semiconductor nanostructures and upscaling to semi-classical models, Evaluation Colloquium of the DFG Priority Program ``Analysis, Modeling and Simulation of Multiscale Problems'', Bad Honnef, May 20 - 21, 2004.
-
H. Gajewski, Zur Numerik des Ladungsträgertransports in Halbleiterbauelementen, Technische Universität München, Institut fär Technische Elektrophysik, February 5, 2004.
-
J. Rehberg, Elliptische und parabolische Probleme mit unglatten Daten, Technische Universität Darmstadt, Fachbereich Mathematik, December 14, 2004.
-
J. Rehberg, Quasilinear parabolic equations in $L^p$, Nonlinear Elliptic and Parabolic Problems: A Special Tribute to the Work of Herbert Amann, June 28 - 30, 2004, Universität Zürich, Institut für Mathematik, Switzerland, June 29, 2004.
-
J. Rehberg, The two-dimensional van Roosbroeck system has solutions in $L^p$, Workshop ``Advances in Mathematical Semiconductor Modelling: Devices and Circuits'', March 2 - 6, 2004, Chinese-German Centre for Science Promotion, Beijing, China, March 5, 2004.
-
M. Baro, H. Gajewski, R. Hünlich, H.-Chr. Kaiser, Optoelektronische Bauelemente: mikroskopische & makroskopische Modelle, MathInside --- Überall ist Mathematik, event of the DFG Research Center ``Mathematics for Key Technologies'' on the occasion of the Open Day of Urania, Berlin, September 13, 2003 - December 3, 2004.
-
H.-Chr. Kaiser, Classical solutions of van Roosbroeck's equations with discontinuous coefficients and mixed boundary conditions on two-dimensional space domains, 19th GAMM Seminar Leipzig on High-dimensional problems --- Numerical treatment and applications, January 23 - 25, 2003, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, January 25, 2003.
-
J. Rehberg, A combined quantum mechanical and macroscopic model for semiconductors, Workshop on Multiscale problems in quantum mechanics and averaging techniques, December 11 - 12, 2003, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, December 12, 2003.
-
J. Rehberg, Solvability and regularity for parabolic equations with nonsmooth data, International Conference ``Nonlinear Partial Differential Equations'', September 15 - 21, 2003, National Academy of Sciences of Ukraine, Institute of Applied Mathematics and Mechanics, Alushta, September 17, 2003.
 External Preprints
External Preprints
-
D. Abdel, A. Blaustein, C. Chainais-Hillairet, M. Herda, J. Moatti, Existence of solutions and uniform bounds for the stationary semiconductor equations with generation and ionic carriers, Preprint no. 2511.23250, Cornell University, 2025, DOI 10.48550/arXiv.2511.23250 .
Abstract
We consider a stationary drift-diffusion system with ionic charge carriers and external generation of electron and hole charge carriers. This system arises, among other applications, in the context of semiconductor modeling for perovskite solar cells. Thanks to truncation techniques and iterative energy estimates, we show the existence and uniform upper and lower bounds on the solutions. The dependency of the bounds on the various parameters of the model is investigated numerically on physically relevant test cases. -
D. Abdel, M. Herda, M. Ziegler, C. Chainais-Hillairet, B. Spetzler, P. Farrell, Numerical analysis and simulation of lateral memristive devices: Schottky, ohmic, and multi-dimensional electrode models, Preprint no. 15065, Cornell University, 2024, DOI 10.48550/arXiv.2412.15065 .
Abstract
In this paper, we present the numerical analysis and simulations of a multi-dimensional memristive device model. Memristive devices and memtransistors based on two-dimensional (2D) materials have demonstrated promising potential as components for next-generation artificial intelligence (AI) hardware and information technology. Our charge transport model describes the drift-diffusion of electrons, holes, and ionic defects self-consistently in an electric field. We incorporate two types of boundary models: ohmic and Schottky contacts. The coupled drift-diffusion partial differential equations are discretized using a physics-preserving Voronoi finite volume method. It relies on an implicit time-stepping scheme and the excess chemical potential flux approximation. We demonstrate that the fully discrete nonlinear scheme is unconditionally stable, preserving the free-energy structure of the continuous system and ensuring the non-negativity of carrier densities. Novel discrete entropy-dissipation inequalities for both boundary condition types in multiple dimensions allow us to prove the existence of discrete solutions. We perform multi-dimensional simulations to understand the impact of electrode configurations and device geometries, focusing on the hysteresis behavior in lateral 2D memristive devices. Three electrode configurations - side, top, and mixed contacts - are compared numerically for different geometries and boundary conditions. These simulations reveal the conditions under which a simplified one-dimensional electrode geometry can well represent the three electrode configurations. This work lays the foundations for developing accurate, efficient simulation tools for 2D memristive devices and memtransistors, offering tools and guidelines for their design and optimization in future applications. -
D. Abdel, J. Relle, Th. Kirchartz, P. Jaap, J. Fuhrmann, S. Burger, Ch. Becker, K. Jäger, P. Farrell, Unravelling the mystery of enhanced open-circuit voltages in nanotextured perovskite solar cells, Preprint no. 2506.10691, Cornell University, 2025, DOI 10.48550/arXiv.2506.10691 .
Abstract
Perovskite solar cells have reached power conversion efficiencies that rival those of established silicon photovoltaic technologies. Nanotextures in perovskite solar cells optimise light trapping and scattering, thereby improving optical absorption. In addition, nanotextures have been experimentally shown to enhance electronic performance, in particular, by increasing the open- circuit voltage VOC ? a phenomenon that, until now, has remained not fully understood. This study investigates the underlying reasons by combining multi-dimensional optical and charge- transport simulations for a single-junction perovskite solar cell. Our results reveal that the increased open-circuit voltage is not driven by optical effects but by the textured geometry itself. For voltages near VOC, texturing one of the absorber/transport layer interfaces increases the imbalance between electron and hole densities in the absorber, thereby reducing Shockley-Read- Hall (SRH) recombination, which is the dominant loss mechanism in this study. While idealised solar cells benefit unconditionally from increasing texture height, in realistic cells there is an optimal texture height which maximizes the power conversion efficiency. These findings provide new insights into the opto-electronic advantages of texturing and offer guidance for the design of next-generation textured perovskite-based solar cells, light emitting diodes, and photodetectors. -
R. Finn, M. O'Donovan, Th. Koprucki, S. Schulz, Theoretical study of the impact of carrier density screening on Urbach tail energies and optical polarization in (Al,Ga)N quantum well systems, Preprint no. arXiv:2501.16808, Cornell University, 2025, DOI 10.48550/arXiv.2501.16808 .
Abstract
Aluminium Gallium Nitride ((Al,Ga)N) presents an ideal platform for designing ultra-violet (UV) light emitters across the entire UV spectral range. However, in the deep-UV spectral range (<280 nm) these emitters exhibit very low quantum efficiencies, which in part is linked to the light polarization characteristics of (Al,Ga)N quantum wells (QWs). In this study we provide insight into the degree of optical polarization of (Al,Ga)N QW systems operating across the UV-C spectral range by means of an atomistic, multi-band electronic structure model. Our model not only captures the difference in valence band ordering in AlN and GaN, it accounts also for alloy disorder induced band mixing effects originating from random alloy fluctuations in (Al,Ga)N QWs. The latter aspect is not captured in widely employed continuum based models. The impact of alloy disorder on the electronic structure is studied in terms of Urbach tail energies, which reflect the broadening of the valence band density of states due to carrier localization effects. We find that especially in wider wells, Urbach tail energies are reduced with increasing carrier densities in the well, highlighting that alloy disorder induced carrier localization effects in (Al,Ga)N QWs are also tightly linked to electrostatic built-in fields. Our calculations show that for QWs designed to emit at the longer wavelength end of the UV-C spectrum, carrier density and well width are of secondary importance for their light emission properties, meaning that one observes mainly transverse electrical polarization. However, for (Al,Ga)N QWs with high Al contents, we find that both well width and carrier density will impact the degree of optical polarization. Our calculations suggest that wider wells will increase the degree of optical polarization and may therefore be a viable option to improve the light extraction efficiency in deep UV light emitters. -
B. Spetzler, E. Spetzler, S. Zamankhani, D. Abdel, P. Farrell, K.-U. Sattler, M. Ziegler, Physics-guided sequence modeling for fast simulation and design Exploration of 2D memristive devices, Preprint no. 2505.13882, Cornell University, 2025, DOI 10.48550/arXiv.2505.13882 .
Abstract
Modeling hysteretic switching dynamics in memristive devices is computationally demanding due to coupled ionic and electronic transport processes. This challenge is particularly relevant for emerging two-dimensional (2D) devices, which feature high-dimensional design spaces that remain largely unexplored. We introduce a physics-guided modeling framework that integrates high-fidelity finite-volume (FV) charge transport simulations with a long short-term memory (LSTM) artificial neural network (ANN) to predict dynamic current-voltage behavior. Trained on physically grounded simulation data, the ANN surrogate achieves more than four orders of magnitude speedup compared to the FV model, while maintaining direct access to physically meaningful input parameters and high accuracy with typical normalized errors <1%. This enables iterative tasks that were previously computationally prohibitive, including inverse modeling from experimental data, design space exploration via metric mapping and sensitivity analysis, as well as constrained multi-objective design optimization. Importantly, the framework preserves physical interpretability via access to detailed spatial dynamics, including carrier densities, vacancy distributions, and electrostatic potentials, through a direct link to the underlying FV model. Our approach establishes a scalable framework for efficient exploration, interpretation, and model-driven design of emerging 2D memristive and neuromorphic devices. -
G. Alì, P. Farrell, N. Rotundo, Forward lateral photovoltage scanning problem: Perturbation approach and existence-uniqueness analysis, Preprint no. arXiv:2404.10466, Cornell University, 2024, DOI 10.48550/arXiv.2404.10466 .
Abstract
In this paper, we present analytical results for the so-called forward lateral photovoltage scanning (LPS) problem. The (inverse) LPS model predicts doping variations in crystal by measuring the current leaving the crystal generated by a laser at various positions. The forward model consists of a set of nonlinear elliptic equations coupled with a measuring device modeled by a resistance. Standard methods to ensure the existence and uniqueness of the forward model cannot be used in a straightforward manner due to the presence of an additional generation term modeling the effect of the laser on the crystal. Hence, we scale the original forward LPS problem and employ a perturbation approach to derive the leading order system and the correction up to the second order in an appropriate small parameter. While these simplifications pose no issues from a physical standpoint, they enable us to demonstrate the analytic existence and uniqueness of solutions for the simplified system using standard arguments from elliptic theory adapted to the coupling with the measuring device. -
P. Farrell, J. Moatti, M. O'Donovan, S. Schulz, Th. Koprucki, Importance of satisfying thermodynamic consistency in light emitting diode simulations, Preprint no. hal-04012467, Hyper Articles en Ligne (HAL), 2023.
Abstract
We show the importance of using a thermodynamically consistent flux discretization when describing drift-diffusion processes within light emitting diode simulations. Using the classical Scharfetter-Gummel scheme with Fermi-Dirac statistics is an example of such an inconsistent scheme. In this case, for an (In,Ga)N multi quantum well device, the Fermi levels show steep gradients on one side of the quantum wells which are not to be expected. This result originates from neglecting diffusion enhancement associated with Fermi-Dirac statistics in the numerical flux approximation. For a thermodynamically consistent scheme, such as the SEDAN scheme, the spikes in the Fermi levels disappear. We will show that thermodynamic inconsistency has far reaching implications on the current-voltage curves and recombination rates. -
S. Piani, P. Farrell, W. Lei, N. Rotundo, L. Heltai, A weighted hybridizable discontinuous Galerkin method for drift-diffusion problems, Preprint no. arXiv:2211.02508, Cornell University, 2022, DOI 10.48550/arXiv.2211.02508 .
-
S. Piani, P. Farrell, W. Lei, N. Rotundo, L. Heltai, Data-driven solutions of ill-posed inverse problems arising from doping reconstruction in semiconductors, Preprint no. arXiv:2208.00742, Cornell University, 2022, DOI 10.48550/arXiv.2208.00742 .
-
M. Oliva, T. Flissikowsky, M. Góra, J. Lähnemann, J. Herranz, R. Lewis, O. Marquardt, M. Ramsteiner, L. Geelhaar, O. Brandt, Carrier recombination in highly uniform and phase-pure GaAs/(Al,Ga)As core/shell nanowire arrays on Si(111): Mott transition and internal quantum efficiency, Preprint no. arXiv:2211.17167, Cornell University, 2022, DOI 10.48550/arXiv.2211.17167 .
Abstract
GaAs-based nanowires are among the most promising candidates for realizing a monolithical integration of III-V optoelectronics on the Si platform. To realize their full potential for applications as light absorbers and emitters, it is crucial to understand their interaction with light governing the absorption and extraction efficiency, as well as the carrier recombination dynamics determining the radiative efficiency. Here, we study the spontaneous emission of zincblende GaAs/(Al,Ga)As core/shell nanowire arrays by μ -photoluminescence spectroscopy. These ordered arrays are synthesized on patterned Si(111) substrates using molecular beam epitaxy, and exhibit an exceptionally low degree of polytypism for interwire separations exceeding a critical value. We record emission spectra over more than five orders of excitation density for both steady-state and pulsed excitation to identify the nature of the recombination channels. An abrupt Mott transition from excitonic to electron-hole-plasma recombination is observed, and the corresponding Mott density is derived. Combining these experiments with simulations and additional direct measurements of the external quantum efficiency using a perfect diffuse reflector as reference, we are able to extract the internal quantum efficiency as a function of carrier density and temperature as well as the extraction efficiency of the nanowire array. The results vividly document the high potential of GaAs/(Al,Ga)As core/shell nanowires for efficient light emitters integrated on the Si platform. Furthermore, the methodology established in this work can be applied to nanowires of any other materials system of interest for optoelectronic applications. -
M. O'Donovan, P. Farrell, T. Streckenbach, Th. Koprucki, S. Schulz, Multiscale simulations of uni-polar hole transport in (In,Ga)N quantum well systems, Preprint no. arXiv:2111.01644, Cornell University Library, arXiv.org, 2021.
Abstract
Understanding the impact of the alloy micro-structure on carrier transport becomes important when designing III-nitride-based LED structures. In this work, we study the impact of alloy fluctuations on the hole carrier transport in (In,Ga)N single and multi-quantum well systems. To disentangle hole transport from electron transport and carrier recombination processes, we focus our attention on uni-polar (p-i-p) systems. The calculations employ our recently established multi-scale simulation framework that connects atomistic tight-binding theory with a macroscale drift-diffusion model. In addition to alloy fluctuations, we pay special attention to the impact of quantum corrections on hole transport. Our calculations indicate that results from a virtual crystal approximation present an upper limit for the hole transport in a p-i-p structure in terms of the current-voltage characteristics. Thus we find that alloy fluctuations can have a detrimental effect on hole transport in (In,Ga)N quantum well systems, in contrast to uni-polar electron transport. However, our studies also reveal that the magnitude by which the random alloy results deviate from virtual crystal approximation data depends on several factors, e.g. how quantum corrections are treated in the transport calculations. -
M. Baro, M. Demuth, E. Giere, Stable continuous spectra for differential operators of arbitrary order, Preprint no. 6, Technische Universität Clausthal, Institut für Mathematik, 2002.
Contact
Mathematical Context
- Algorithms for the generation of 3D boundary conforming Delaunay meshes
- Analysis of Partial Differential Equations and Evolutionary Equations
- Numerical Methods for PDEs with Stochastic Data
- Numerical methods for problems from fluid dynamics
- Systems of partial differential equations: modeling, numerical analysis and simulation