Background
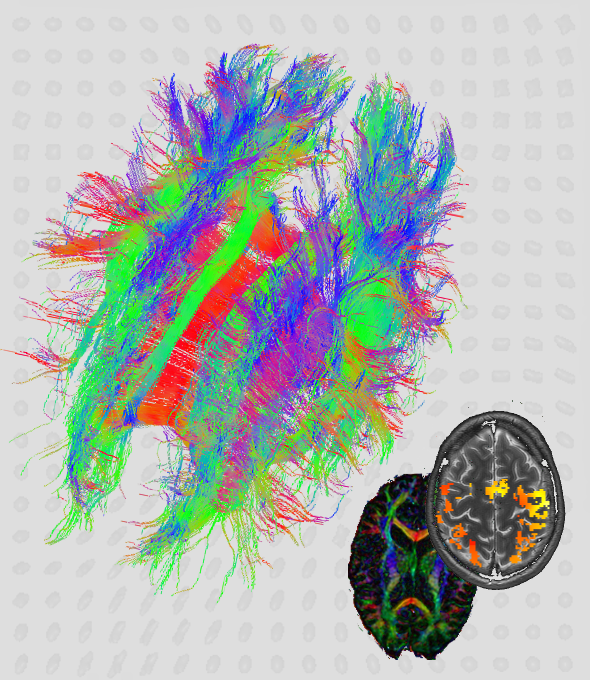
According to current studies, the international trend in the scientific landscape shows an increase of research in interdisciplinary problems. This observed increase in the significance of the interdisciplinary research topics results from the necessity of analyzing current, socially relevant topics (such as climate change or energy and health issues) using a combination of natural, life and social sciences, i.e. with an increasingly integrated approach to investigate and solve questions.
The task of developing adequate and up-to-date methods for analysis and information generation is the result of the high information and data volumes characteristic of the problems under consideration as well as the growing importance of simulation and optimization of technological and social processes. A connecting element in this context is mathematics. Modern methods of mathematical modeling and simulation (short: MMS) have proven to be a fundamental resource of scientific and technological progress. They enable:
- the reliable extraction of information from large data sets
- the avoidance of expensive experiments in basic research in industry and science, which are energy-intensive and damaging for the environment ("virtual laboratory")
- to obtain knowledge on experiments for inaccessible space and time scales ("high-performance microscope" or "high-performance telescope")
- the shortening of development cycles and the reduction of development costs for new products as well as an increase in efficiency and quality of production processes
- reliable predictions for dangerous or impossible experiments (climate, environment, medicine) and secure estimation procedures in Humanities, Economics and Social Sciences
- the analysis and utilization of the influence of random (stochastic) events
- a risk assessment in the use of new technologies and in environmental and social policy
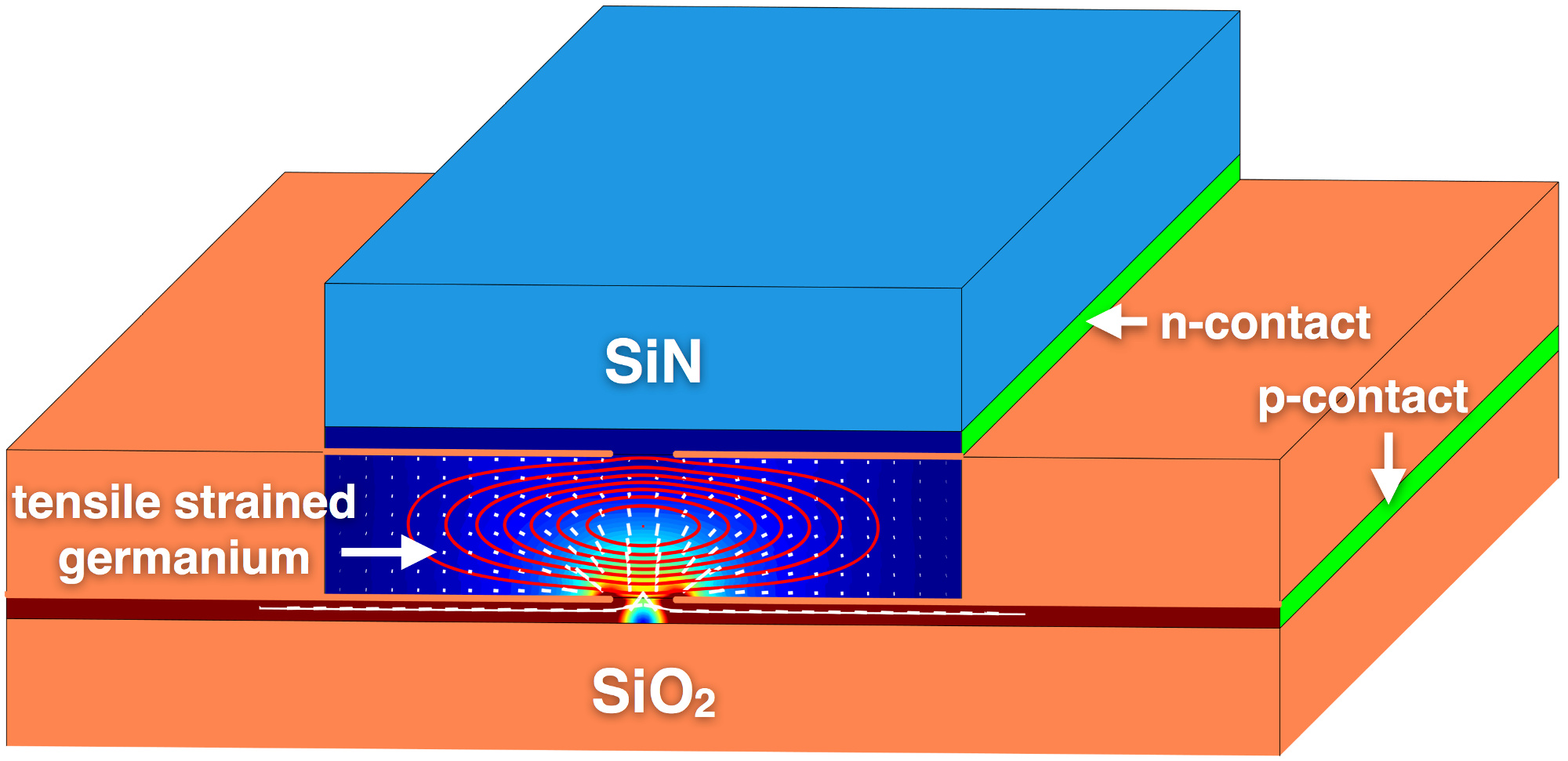
Mathematical modeling and simulation is therefore an important methodological topic both in the natural and engineering sciences as well as in the economic, social, life and environmental sciences. Methods from very different areas of mathematics are used (eg. statistics, mathematical finance, optimization, numerical solutions of partial differential equations, mathematical image processing, etc.) and problems arise on every conceivable spatial and time scales (from nanoparticles to large-scale cosmic structures, from the femtosecond to the age of the universe) and at various levels of complexity (from the individual company to the entire global economy, from local environmental events to global climate models).
Common to all these methods is the fact that they are based on mathematical principles. As such, they have a cross-section nature, this means that the respective methods can generally be used not only in the specific application context, but also in the case of problems in completly different branches of science. Herein lies the great potential for its effective use.

