Materials Modeling

Many important processes of industrial production and use of modern and functional materials are accompanied by phase transitions and hysteresis. In tight collaboration with users from industry, physics and chemistry existing as well as newly developed models are studied at WIAS regarding their practical relevance.

Coagulation

Coagulation processes are typical in physics (merging of particles, growth of gas bubbles), meteorology (merging of droplets in clouds, transportation of aerosols), chemistry (hydrogels, formation of aerosols), chemistry (hydrogels, formation of soot), astrophysics (formation of planets). At WIAS, different types of models are investigated: probabilistically with complex Markov processes, analytically with kinetic equations and their properties, numerically with solvability and computational questions for these equations, and heuristically with theoretical descriptions. One of the main questions is under which conditions particularly large particles are formed in large systems, i.e. the occurrence of the gelation phase transition.

Phase field models for complex materials and interfaces

This research topic focusses on modeling complex material systems with different phases including multiphase and interfacial flows, damage and fatigue modeling, topology optimization and complex materials. Physical phenomena modelled involve fluid flow, diffuse transport and (visco)elastic deformation in the context of phase separation and phase transitions. Applications range from biology to physics and engineering.

Mathematical Models and Methods for Lithium-ion Batteries

In modern lithium-ion batteries, a variety of physicochemical processes occur simultaneously on various size and time scales. To systematically examine their influence and interactions within a battery, mathematical models are developed that represent the respective processes using partial differential equations. Using numerical methods, specific parameters of a battery can be calculated, such as the cell voltage as a function of state of charge. These models are continuously evolving to, for example, account for aging effects.

Modeling, Simulation and Optimization for Biomedical Applications

Mathematical models and computational techniques are nowadays utilized in medical sciences for noninvasive diagnostic, diseases characterization, therapy planning, and treatment monitoring. The research at WIAS focuses on efficient and robust models for biological tissues and fluids, on the usage of advanced mathematical models in data assimilation and medical imaging applications, as well as on techniques in optimization, machine learning, and optimal control for decision support in biomedicine.

Diffusion models in statistical physics

Many models in statistical physics contain random paths with interactions of various natures, like polymer models, where the path has a self-repellence and attractive interactions with the surrounding medium, or mass transport models in random medium, where the path carries a random mass that is increased and decreased, depending on the properties of the space visited, or self-intersection properties of the path. Also coupled nonlinear diffusion equations are used for modeling such phenomena.

Modeling of thin films and nano structures on substrates

Thin films play an important role in nature and many areas of technological applications. In particular on micro- and nanoscales technological processes such as dewetting or epitaxial growth are used to design surfaces with specific material properties. Apart from the need to derive mathematical decriptions, analyis and numerical simulation, that serve to accelerate the development of new technologies, it is also exciting to understand material behaviour on these small scales.

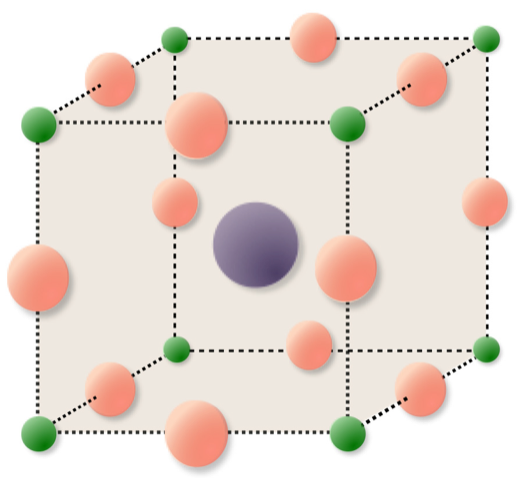
Electronic materials

Novel electronic materials require advanced charge transport modeling and simulation techniques in which moving ions on the crystal lattice cannot be neglected. Examples of such materials are perovskites and 2D layered transition metal dichalcogenides (TMDCs) like molybdenum disulfide. They play a fundamental role for applications like solar cells as well as memristive devices.

Particle-based modeling in the Sciences

For more than a hundred years diverse processes and phenomena in the natural sciences have been modelled using random particle systems. At the WIAS macroscopic phenomena in such large systems are analyzed with particular focus on phase transitions such as percolation or gelation.

Nonlinear material models, multifunctional materials and hysteresis in continuum mechanics.

Many components in modern equipment rely on specific properties of so-called multifunctional materials. These materials are distinguished by the fact that therein properties like elastic deformability, thermal expansibility, magnetizability, or polarizability interact nontrivially like for instance in a piezo-crystal. At WIAS coupled models describing these properties are developed and analyzed.