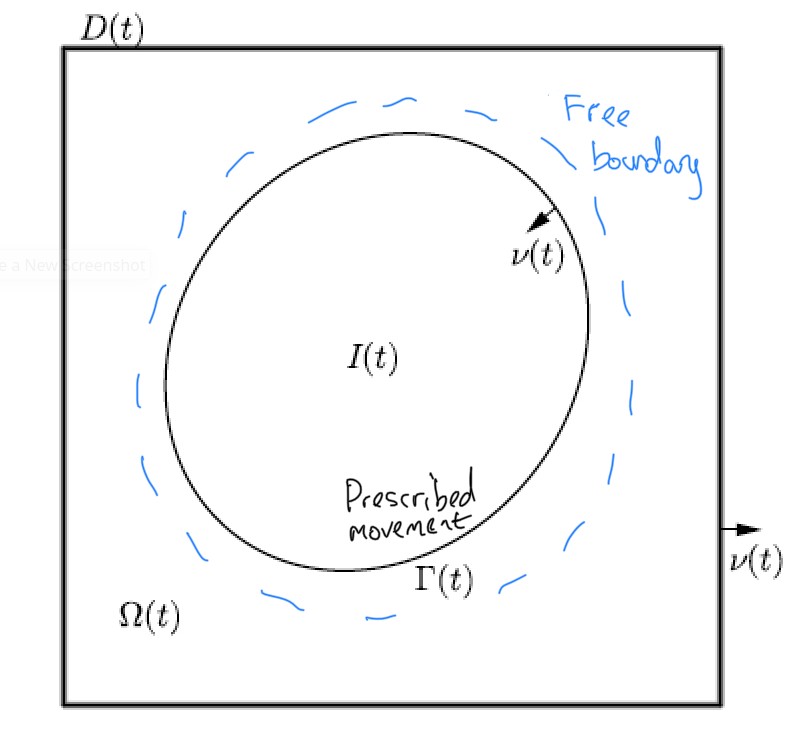
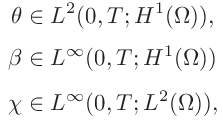 | Properties of solutions to free boundary problems: |
 | Phase-field approximation of free boundary problems: |
 | Free-boundary problems in the thin-film geometry |
 | Variational inequalities and (implicit) obstacle problems |
 | PDEs on evolving domains and surfaces |
 | Organization of conferences/workshops dealing with free boundary problems |
Publications
 Monographs
Monographs
-
M. Hintermüller, R. Herzog, Ch. Kanzow, M. Ulbrich, S. Ulbrich, eds., Non-Smooth and Complementarity-Based Distributed Parameter Systems: Simulation and Hierarchical Optimization, 172 of International Series of Numerical Mathematics, Birkhäuser, Springer Nature Switzerland AG, Cham, 2022, viii + 519 pages, (Collection Published), DOI 10.1007/978-3-030-79393-7 .
-
M. Hintermüller, J.F. Rodrigues, eds., Topics in Applied Analysis and Optimisation -- Partial Differential Equations, Stochastic and Numerical Analysis, CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, 396 pages, (Collection Published).
-
M. Hintermüller, D. Wegner, Distributed and Boundary Control Problems for the Semidiscrete Cahn--Hilliard/Navier--Stokes System with Nonsmooth Ginzburg--Landau Energies, in: Topological Optimization and Optimal Transport in the Applied Sciences, M. Bergounioux, E. Oudet, M. Rumpf, G. Carlier, Th. Champion, F. Santambrogio, eds., 17 of Radon Series on Computational and Applied Mathematics, De Gruyter, Berlin, 2017, pp. 40--63, (Chapter Published).
-
H.-Chr. Kaiser, D. Knees, A. Mielke, J. Rehberg, E. Rocca, M. Thomas, E. Valdinoci, eds., PDE 2015: Theory and Applications of Partial Differential Equations, 10 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Science, Springfield, 2017, iv+933 pages, (Collection Published).
-
E. Valdinoci, ed., Contemporary PDEs between theory and applications, 35 of Discrete and Continuous Dynamical Systems Series A, American Institute of Mathematical Sciences, Springfield, 2015, 625 pages, (Collection Published).
-
P. Colli, A. Damlamian, N. Kenmochi, M. Mimura, J. Sprekels, eds., Proceedings of International Conference on: Nonlinear Phenomena with Energy Dissipation: Mathematical Analysis, Modeling and Simulation, 29 of Gakuto International Series Mathematical Sciences and Applications, Gakkōtosho, Tokyo, 2008, 475 pages, (Collection Published).
-
P. Colli, N. Kenmochi, J. Sprekels, eds., Dissipative Phase Transitions, 71 of Series on Advances in Mathematics for Applied Sciences, World Scientific, Singapore, 2006, xii+300 pages, (Collection Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
J.S. Dokken, P.E. Farrell, B. Keith, I. Papadopoulos, Th.M. Surowiec, The latent variable proximal point algorithm for variational problems with inequality constraints, Computer Methods in Applied Mechanics and Engineering, 445 (2025), pp. 118181/x--118181/xx, DOI 10.1016/j.cma.2025.118181 .
Abstract
The latent variable proximal point (LVPP) algorithm is a framework for solving infinite-dimensional variational problems with pointwise inequality constraints. The algorithm is a saddle point reformulation of the Bregman proximal point algorithm. At the continuous level, the two formulations are equivalent, but the saddle point formulation is more amenable to discretization because it introduces a structure-preserving transformation between a latent function space and the feasible set. Working in this latent space is much more convenient for enforcing inequality constraints than the feasible set, as discretizations can employ general linear combinations of suitable basis functions, and nonlinear solvers can involve general additive updates. LVPP yields numerical methods with observed mesh-independence for obstacle problems, contact, fracture, plasticity, and others besides; in many cases, for the first time. The framework also extends to more complex constraints, providing means to enforce convexity in the Monge?Ampère equation and handling quasi-variational inequalities, where the underlying constraint depends implicitly on the unknown solution. In this paper, we describe the LVPP algorithm in a general form and apply it to twelve problems from across mathematics. -
A. Alphonse, C. Christof, M. Hintermüller, I. Papadopoulos, A globalized inexact semismooth Newton method for nonsmooth fixed--point equations involving variational inequalities, Computational Optimization and Applications. An International Journal, pp. 1--55 (published online 10.11.2025), DOI 10.1007/s10589-025-00722-8 .
Abstract
We develop a semismooth Newton framework for the numerical solution of fixed-point equations that are posed in Banach spaces. The framework is motivated by applications in the field of obstacle-type quasi-variational inequalities and implicit obstacle problems. It is discussed in a general functional analytic setting and allows for inexact function evaluations and Newton steps. Moreover, if a certain contraction assumption holds, we show that it is possible to globalize the algorithm by means of the Banach fixed-point theorem and to ensure q-superlinear convergence to the problem solution for arbitrary starting values. By means of a localization technique, our Newton method can also be used to determine solutions of fixed-point equations that are only locally contractive and not uniquely solvable. We apply our algorithm to a quasi-variational inequality which arises in thermoforming and which not only involves the obstacle problem as a source of nonsmoothness but also a semilinear PDE containing a nondifferentiable Nemytskii operator. Our analysis is accompanied by numerical experiments that illustrate the mesh-independence and q -superlinear convergence of the developed solution algorithm. -
A. Alphonse, G. Wachsmuth, Subdifferentials and penalty approximations of the obstacle problem, SIAM Journal on Optimization, 35 (2025), pp. 3/2017--3/2039, DOI 10.1137/24M172202X .
Abstract
We consider a framework for approximating the obstacle problem through a penalty approach by nonlinear PDEs. By using tools from capacity theory, we show that derivatives of the solution maps of the penalized problems converge in the weak operator topology to an element of the strong-weak Bouligand subdifferential. We are able to treat smooth penalty terms as well as nonsmooth ones involving, for example, the positive part function max(0, cdot ). Our abstract framework applies to several specific choices of penalty functions which are omnipresent in the literature. We conclude with consequences to the theory of optimal control of the obstacle problem -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, G. Wachsmuth, Minimal and maximal solution maps of elliptic QVIs of obstacle type: Lipschitz stability, differentiability, and optimal control, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 27 (2025), pp. 4/521--4/573, DOI 10.4171/IFB/545 .
Abstract
Quasi-variational inequalities (QVIs) of obstacle type in many cases have multiple solutions that can be ordered. We study a multitude of properties of the operator mapping the source term to the minimal or maximal solution of such QVIs. We prove that the solution maps are locally Lipschitz continuous and directionally differentiable and show existence of optimal controls for problems that incorporate these maps as the control-to-state operator. We also consider a Moreau?Yosida-type penalisation for the QVI wherein we show that it is possible to approximate the minimal and maximal solutions by sequences of minimal and maximal solutions (respectively) of certain PDEs, which have a simpler structure and offer a convenient characterisation in particular for computation. For solution mappings of these penalised problems, we prove a number of properties including Lipschitz and differential stability. Making use of the penalised equations, we derive (in the limit) C-stationarity conditions for the control problem, in addition to the Bouligand stationarity we get from the differentiability result. -
L. Schmeller, D. Peschka, Sharp-interface limits of Cahn--Hilliard models and mechanics with moving contact lines, Multiscale Modeling & Simulation. A SIAM Interdisciplinary Journal, 22 (2024), pp. 869--890, DOI 10.1137/23M1546592 .
Abstract
We construct gradient structures for free boundary problems with moving capillary interfaces with nonlinear (hyper)elasticity and study the impact of moving contact lines. In this context, we numerically analyze how phase-field models converge to certain sharp-interface models when the interface thickness tends to zero. In particular, we study the scaling of the Cahn--Hilliard mobility with certain powers of the interfacial thickness. In the presence of interfaces, it is known that the intended sharp-interface limit holds only for a particular range of powers However, in the presence of moving contact lines we show that some scalings that are valid for interfaces produce significant errors and the effective range of valid powers of the interfacial thickness in the mobility reduces. -
A. Erhardt, Cardiac dynamics of a human ventricular tissue model with focus on early afterdepolarizations, Frontiers in Physics, section Biophysics, 13 (2025), pp. 1569121/1--1569121/15, DOI 10.3389/fphy.2025.1569121 .
Abstract
The paper is aimed to investigate computationally complex cardiac dynamics of the famous human ventricular model of ten Tusscher and Panfilov from 2006. The corresponding physical system is modeled by a set of nonlinear differential equations containing various of system parameters. In case a specific physical parameter crosses a certain threshold, the system is forced to change dynamics, which might result in dangerous cardiac dynamics and can be precursors to cardiac death. For the performance of an efficient numerical analysis the original model is remodeled and simplified in such a way that the modified models perfectly matches the trajectory of the original model. Moreover, it is demonstrated that the simplified models have the same dynamics. Furthermore, using the lowest dimensional model it is systematically shown by means of bifurcation analysis that combinations of reduced slow and rapid potassium channels and enhanced sodium channel may lead to early afterdepolarizations. Finally, synchronization and the effect of EADs on larger scale (macro scale) is investigated numerically by studying the corresponding monodomain model. To this end we study the pattern formation of an one dimensional network of epi-, mid-myo- and endocardial cells and a two dimensional epicardial monodomain equation. -
A. Erhardt, Cardiac dynamics of a human ventricular tissue model with focus on early afterdepolarizations, , 13 (2025), pp. 1569121/1--1569121/15, DOI 10.3389/fphy.2025.1569121 .
Abstract
The paper is aimed to investigate computationally complex cardiac dynamics of the famous human ventricular model of ten Tusscher and Panfilov from 2006. The corresponding physical system is modeled by a set of nonlinear differential equations containing various of system parameters. In case a specific physical parameter crosses a certain threshold, the system is forced to change dynamics, which might result in dangerous cardiac dynamics and can be precursors to cardiac death. For the performance of an efficient numerical analysis the original model is remodeled and simplified in such a way that the modified models perfectly matches the trajectory of the original model. Moreover, it is demonstrated that the simplified models have the same dynamics. Furthermore, using the lowest dimensional model it is systematically shown by means of bifurcation analysis that combinations of reduced slow and rapid potassium channels and enhanced sodium channel may lead to early afterdepolarizations. Finally, synchronization and the effect of EADs on larger scale (macro scale) is investigated numerically by studying the corresponding monodomain model. To this end we study the pattern formation of an one dimensional network of epi-, mid-myo- and endocardial cells and a two dimensional epicardial monodomain equation. -
D. Peschka, Partial and complete wetting of thin films with dynamic contact angle, Physics of Fluids, 35 (2023), pp. 041705/1--041705/6, DOI 10.1063/5.0146538 .
Abstract
The wetting of thin films depends critically on the sign of the spreading coefficient S. We discuss the cases S<0, S=0, and S>0 for transient models with contact line dissipation and find that the use of a dynamic contact angle solves problems for S>0 that models might otherwise have. For initial data with a non-zero slope and S>0, we show that there exists a finite time at which the contact angle of the thin film goes to zero. Then, a molecular precursor emerges from the thin film and moves outward at a constant velocity. -
A.K. Barua, R. Chew, L. Shuwang, J. Lowengrub, A. Münch, B. Wagner, Sharp-interface problem of the Ohta--Kawasaki model for symmetric diblock copolymers, Journal of Computational Physics, 481 (2023), pp. 112032/1--112032/23, DOI 10.1016/j.jcp.2023.112032 .
Abstract
The Ohta-Kawasaki model for diblock-copolymers is well known to the scientific community of diffuse-interface methods. To accurately capture the long-time evolution of the moving interfaces, we present a derivation of the corresponding sharp-interface limit using matched asymptotic expansions, and show that the limiting process leads to a Hele-Shaw type moving interface problem. The numerical treatment of the sharp-interface limit is more complicated due to the stiffness of the equations. To address this problem, we present a boundary integral formulation corresponding to a sharp interface limit of the Ohta-Kawasaki model. Starting with the governing equations defined on separate phase domains, we develop boundary integral equations valid for multi-connected domains in a 2D plane. For numerical simplicity we assume our problem is driven by a uniform Dirichlet condition on a circular far-field boundary. The integral formulation of the problem involves both double- and single-layer potentials due to the modified boundary condition. In particular, our formulation allows one to compute the nonlinear dynamics of a non-equilibrium system and pattern formation of an equilibrating system. Numerical tests on an evolving slightly perturbed circular interface (separating the two phases) are in excellent agreement with the linear analysis, demonstrating that the method is stable, efficient and spectrally accurate in space. -
L. Giacomelli, M. Gnann, D. Peschka, Droplet motion with contact-line friction: Long-time asymptotics in complete wetting, Proceedings of The Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, 479 (2023), pp. 20230090/1--20230090/23, DOI 10.1098/rspa.2023.0090 .
Abstract
We consider the thin-film equation for a class of free boundary conditions modelling friction at the contact line, as introduced by E and Ren. Our analysis focuses on formal long-time asymptotics of solutions in the perfect wetting regime. In particular, through the analysis of quasi-self-similar solutions, we characterize the profile and the spreading rate of solutions depending on the strength of friction at the contact line, as well as their (global or local) corrections, which are due to the dynamical nature of the free boundary conditions. These results are complemented with full transient numerical solutions of the free boundary problem. -
M. Hintermüller, T. Keil, Strong stationarity conditions for the optimal control of a Cahn--Hilliard--Navier--Stokes system, Applied Mathematics and Optimization. An International Journal with Applications to Stochastics, 89 (2024), pp. 12/1--12/28 (published online on 05.12.2023), DOI 10.1007/s00245-023-10063-9 .
Abstract
This paper is concerned with the distributed optimal control of a time-discrete Cahn-Hilliard-Navier-Stokes system with variable densities. It focuses on the double-obstacle potential which yields an optimal control problem for a variational inequality of fourth order and the Navier-Stokes equation. The existence of solutions to the primal system and of optimal controls is established. The Lipschitz continuity of the constraint mapping is derived and used to characterize the directional derivative of the constraint mapping via a system of variational inequalities and partial differential equations. Finally, strong stationarity conditions are presented following an approach from Mignot and Puel. -
A.H. Erhardt, E. Wahlén, J. Weber, Bifurcation analysis for axisymmetric capillary water waves with vorticity and swirl, Studies in Applied Mathematics, 149 (2022), pp. 904--942, DOI 10.1111/sapm.12525 .
Abstract
We study steady axisymmetric water waves with general vorticity and swirl, subject to the influence of surface tension. This can be formulated as an elliptic free boundary problem in terms of Stokes' stream function. A change of variables allows us to overcome the generic coordinate-induced singularities and to cast the problem in the form ?identity plus compact,? which is amenable to Rabinowitz's global bifurcation theorem, whereas no restrictions regarding the absence of stagnation points in the flow have to be made. Within the scope of this new formulation, local curves and global families of solutions, bifurcating from laminar flows with a flat surface, are constructed. -
A.K. Giri, P. Malgaretti, D. Peschka, M. Sega, Resolving the microscopic hydrodynamics at the moving contact line, Physical Review Fluids, 7 (2022), pp. L102001/1--L102001/9, DOI 10.1103/PhysRevFluids.7.L102001 .
Abstract
By removing the smearing effect of capillary waves in molecular dynamics simulations we are able to provide a microscopic picture of the region around the moving contact line (MCL) at an unprecedented resolution. On this basis, we show that the continuum character of the velocity field is unaffected by molecular layering down to below the molecular scale. The solution of the continuum Stokes problem with MCL and Navier-slip matches very well the molecular dynamics data and is consistent with a slip-length of 42 Å and small contact line dissipation. This is consistent with observations of the local force balance near the liquid-solid interface. -
A. Alphonse, C.N. Rautenberg, J.F. Rodrigues, Analysis of a quasi-variational contact problem arising in thermoelasticity, Nonlinear Analysis. An International Mathematical Journal, 217 (2022), pp. 112728/1--112728/40, DOI 10.1016/j.na.2021.112728 .
Abstract
We formulate and study two mathematical models of a thermoforming process involving a membrane and a mould as implicit obstacle problems. In particular, the membrane-mould coupling is determined by the thermal displacement of the mould that depends in turn on the membrane through the contact region. The two models considered are a stationary (or elliptic) model and an evolutionary (or quasistatic) one. For the first model, we prove the existence of weak solutions by solving an elliptic quasi-variational inequality coupled to elliptic equations. By exploring the fine properties of the variation of the contact set under non-degenerate data, we give sufficient conditions for the existence of regular solutions, and under certain contraction conditions, also a uniqueness result. We apply these results to a series of semi-discretised problems that arise as approximations of regular solutions for the evolutionary or quasistatic problem. Here, under certain conditions, we are able to prove existence for the evolutionary problem and for a special case, also the uniqueness of time-dependent solutions. -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, On the differentiability of the minimal and maximal solution maps of elliptic quasi-variational inequalities, Journal of Mathematical Analysis and Applications, 507 (2022), pp. 125732/1--125732/19, DOI 10.1016/j.jmaa.2021.125732 .
Abstract
In this short note, we prove that the minimal and maximal solution maps associated to elliptic quasi-variational inequalities of obstacle type are directionally differentiable with respect to the forcing term and for directions that are signed. On the way, we show that the minimal and maximal solutions can be seen as monotone limits of solutions of certain variational inequalities and that the aforementioned directional derivatives can also be characterised as the monotone limits of sequences of directional derivatives associated to variational inequalities. -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, Optimal control and directional differentiability for elliptic quasi-variational inequalities, Set-Valued and Variational Analysis. Theory and Applications. Springer, Dordrecht. English., 30 (2022), pp. 873--922, DOI 10.1007/s11228-021-00624-x .
Abstract
We focus on elliptic quasi-variational inequalities (QVIs) of obstacle type and prove a number of results on the existence of solutions, directional differentiability and optimal control of such QVIs. We give three existence theorems based on an order approach, an iteration scheme and a sequential regularisation through partial differential equations. We show that the solution map taking the source term into the set of solutions of the QVI is directionally differentiable for general unsigned data, thereby extending the results of our previous work which provided a first differentiability result for QVIs in infinite dimensions. Optimal control problems with QVI constraints are also considered and we derive various forms of stationarity conditions for control problems, thus supplying among the first such results in this area. -
G. Dong, M. Hintermüller, Y. Zhang, A class of second-order geometric quasilinear hyperbolic PDEs and their application in imaging, SIAM Journal on Imaging Sciences, 14 (2021), pp. 645--688, DOI 10.1137/20M1366277 .
Abstract
In this paper, we study damped second-order dynamics, which are quasilinear hyperbolic partial differential equations (PDEs). This is inspired by the recent development of second-order damping systems for accelerating energy decay of gradient flows. We concentrate on two equations: one is a damped second-order total variation flow, which is primarily motivated by the application of image denoising; the other is a damped second-order mean curvature flow for level sets of scalar functions, which is related to a non-convex variational model capable of correcting displacement errors in image data (e.g. dejittering). For the former equation, we prove the existence and uniqueness of the solution. For the latter, we draw a connection between the equation and some second-order geometric PDEs evolving the hypersurfaces which are described by level sets of scalar functions, and show the existence and uniqueness of the solution for a regularized version of the equation. The latter is used in our algorithmic development. A general algorithm for numerical discretization of the two nonlinear PDEs is proposed and analyzed. Its efficiency is demonstrated by various numerical examples, where simulations on the behavior of solutions of the new equations and comparisons with first-order flows are also documented. -
M. Thomas, S. Tornquist, Discrete approximation of dynamic phase-field fracture in visco-elastic materials, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 3865--3924, DOI 10.3934/dcdss.2021067 .
Abstract
This contribution deals with the analysis of models for phase-field fracture in visco-elastic materials with dynamic effects. The evolution of damage is handled in two different ways: As a viscous evolution with a quadratic dissipation potential and as a rate-independent law with a positively 1-homogeneous dissipation potential. Both evolution laws encode a non-smooth constraint that ensures the unidirectionality of damage, so that the material cannot heal. Suitable notions of solutions are introduced in both settings. Existence of solutions is obtained using a discrete approximation scheme both in space and time. Based on the convexity properties of the energy functional and on the regularity of the displacements thanks to their viscous evolution, also improved regularity results with respect to time are obtained for the internal variable: It is shown that the damage variable is continuous in time with values in the state space that guarantees finite values of the energy functional. -
A. Alphonse, C.N. Rautenberg, J.F. Rodrigues, Analysis of a quasi-variational contact problem arising in thermoelasticity, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 217 (2022), pp. 112728/1--112728/40 (published online on 13.12.2021), DOI 10.1016/j.na.2021.112728 .
Abstract
We formulate and study two mathematical models of a thermoforming process involving a membrane and a mould as implicit obstacle problems. In particular, the membrane-mould coupling is determined by the thermal displacement of the mould that depends in turn on the membrane through the contact region. The two models considered are a stationary (or elliptic) model and an evolutionary (or quasistatic) one. For the first model, we prove the existence of weak solutions by solving an elliptic quasi-variational inequality coupled to elliptic equations. By exploring the fine properties of the variation of the contact set under non-degenerate data, we give sufficient conditions for the existence of regular solutions, and under certain contraction conditions, also a uniqueness result. We apply these results to a series of semi-discretised problems that arise as approximations of regular solutions for the evolutionary or quasistatic problem. Here, under certain conditions, we are able to prove existence for the evolutionary problem and for a special case, also the uniqueness of time-dependent solutions. -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, On the differentiability of the minimal and maximal solution maps of elliptic quasi-variational inequalities, Journal of Mathematical Analysis and Applications, published online on 27.10.2021, DOI 10.1016/j.jmaa.2021.125732 .
Abstract
In this short note, we prove that the minimal and maximal solution maps associated to elliptic quasi-variational inequalities of obstacle type are directionally differentiable with respect to the forcing term and for directions that are signed. On the way, we show that the minimal and maximal solutions can be seen as monotone limits of solutions of certain variational inequalities and that the aforementioned directional derivatives can also be characterised as the monotone limits of sequences of directional derivatives associated to variational inequalities. -
N.A. Dao, J.I. Díaz, Q.B.H. Nguyen, Pointwise gradient estimates in multi-dimensional slow diffusion equations with a singular quenching term, Advanced Nonlinear Studies, 20 (2020), pp. 373--384, DOI 10.1515/ans-2020-2076 .
-
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, Discrete and Continuous Dynamical Systems -- Series S, 14 (2021), pp. 89--119 (published online in March 2020), DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes. In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
A. Alphonse, M. Hintermüller, C.N. Rautenberg, Existence, iteration procedures and directional differentiability for parabolic QVIs, Calculus of Variations and Partial Differential Equations, 59 (2020), pp. 95/1--95/53, DOI 10.1007/s00526-020-01732-6 .
Abstract
We study parabolic quasi-variational inequalities (QVIs) of obstacle type. Under appropriate assumptions on the obstacle mapping, we prove the existence of solutions of such QVIs by two methods: one by time discretisation through elliptic QVIs and the second by iteration through parabolic variational inequalities (VIs). Using these results, we show the directional differentiability (in a certain sense) of the solution map which takes the source term of a parabolic QVI into the set of solutions, and we relate this result to the contingent derivative of the aforementioned map. We finish with an example where the obstacle mapping is given by the inverse of a parabolic differential operator. -
G. Dong, H. Guo, Parametric polynomial preserving recovery on manifolds, SIAM Journal on Scientific Computing, 42 (2020), pp. A1885--A1912, DOI 10.1137/18M1191336 .
-
D. Peschka, S. Haefner, L. Marquant, K. Jacobs, A. Münch, B. Wagner, Signatures of slip in dewetting polymer films, Proceedings of the National Academy of Sciences of the United States of America, 116 (2019), pp. 9275--9284, DOI 10.1073/pnas.1820487116 .
-
E. Meca Álvarez, A. Münch, B. Wagner, Localized instabilities and spinodal decomposition in driven systems in the presence of elasticity, Physical Review E. Statistical, Nonlinear, and Soft Matter Physics, 97 (2018), pp. 012801/1--012801/12, DOI 10.1103/PhysRevE.97.012801 .
Abstract
We study numerically and analytically the instabilities associated with phase separation in a solid layer on which an external material flux is imposed. The first instability is localized within a boundary layer at the exposed free surface by a process akin to spinodal decomposition. In the limiting static case, when there is no material flux, the coherent spinodal decomposition is recovered. In the present problem stability analysis of the time-dependent and non-uniform base states as well as numerical simulations of the full governing equations are used to establish the dependence of the wavelength and onset of the instability on parameter settings and its transient nature as the patterns eventually coarsen into a flat moving front. The second instability is related to the Mullins-Sekerka instability in the presence of elasticity and arises at the moving front between the two phases when the flux is reversed. Stability analyses of the full model and the corresponding sharp-interface model are carried out and compared. Our results demonstrate how interface and bulk instabilities can be analysed within the same framework which allows to identify and distinguish each of them clearly. The relevance for a detailed understanding of both instabilities and their interconnections in a realistic setting are demonstrated for a system of equations modelling the lithiation/delithiation processes within the context of Lithium ion batteries. -
A. Ceretani, C.N. Rautenberg, The Boussinesq system with mixed non-smooth boundary conditions and ``do-nothing'' boundary flow, Zeitschrift fur Angewandte Mathematik und Physik. ZAMP. Journal of Applied Mathematics and Physics. Journal de Mathematiques et de Physique Appliquees, 70 (2019), pp. 14/1--14/24 (published online on 07.12.2018), DOI 10.1007/s00033-018-1058-y .
Abstract
A stationary Boussinesq system for an incompressible viscous fluid in a bounded domain with a nontrivial condition at an open boundary is studied. We consider a novel non-smooth boundary condition associated to the heat transfer on the open boundary that involves the temperature at the boundary, the velocity of the fluid, and the outside temperature. We show that this condition is compatible with two approaches at dealing with the do-nothing boundary condition for the fluid: 1) the directional do-nothing condition and 2) the do-nothing condition together with an integral bound for the backflow. Well-posedness of variational formulations is proved for each problem. -
T. Ahnert, A. Münch, B. Niethammer, B. Wagner, Stability of concentrated suspensions under Couette and Poiseuille flow, Journal of Engineering Mathematics, 111 (2018), pp. 51--77, DOI 10.1007/s10665-018-9954-x .
Abstract
The stability of two-dimensional Poiseuille flow and plane Couette flow for concentrated suspensions is investigated. Linear stability analysis of the two-phase flow model for both flow geometries shows the existence of a convectively driven instability with increasing growth rates of the unstable modes as the particle volume fraction of the suspension increases. In addition it is shown that there exists a bound for the particle phase viscosity below which the two-phase flow model may become ill-posed as the particle phase approaches its maximum packing fraction. The case of two-dimensional Poiseuille flow gives rise to base state solutions that exhibit a jammed and unyielded region, due to shear-induced migration, as the maximum packing fraction is approached. The stability characteristics of the resulting Bingham-type flow is investigated and connections to the stability problem for the related classical Bingham-flow problem are discussed. -
T. Ahnert, A. Münch, B. Wagner, Models for the two-phase flow of concentrated suspensions, European Journal of Applied Mathematics, 30 (2019), pp. 585--617 (published online on 04.06.2018), DOI 10.1017/S095679251800030X .
Abstract
A new two-phase model is derived that make use of a constitutive law combining non-Brownian suspension with granular rheology, that was recently proposed by Boyer et al. [PRL, 107(18),188301 (2011)]. It is shown that for the simple channel flow geometry, the stress model naturally exhibits a Bingham type flow property with an unyielded finite-size zone in the center of the channel. As the volume fraction of the solid phase is increased, the various transitions in the flow fields are discussed using phase space methods for a boundary value problem, that is derived from the full model. The predictions of this analysis is then compared to the direct finite-element numerical solutions of the full model. -
H. Antil, C.N. Rautenberg, Fractional elliptic quasi-variational inequalities: Theory and numerics, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 20 (2018), pp. 1--24, DOI 10.4171/IFB/395 .
-
C. Bertoglio, A. Caiazzo, Y. Bazilevs, M. Braack, M. Esmaily-Moghadam, V. Gravemeier, A.L. Marsden, O. Pironneau, I.E. Vignon-Clementel, W.A. Wall, Benchmark problems for numerical treatment of backflow at open boundaries, International Journal of Numerical Methods in Biomedical Engineering, 34 (2018), pp. e2918/1--e2918/34, DOI 10.1002/cnm.2918 .
Abstract
In computational fluid dynamics, incoming velocity at open boundaries, or backflow, often yields to unphysical instabilities already for moderate Reynolds numbers. Several treatments to overcome these backflow instabilities have been proposed in the literature. However, these approaches have not yet been compared in detail in terms of accuracy in different physiological regimes, in particular due to the difficulty to generate stable reference solutions apart from analytical forms. In this work, we present a set of benchmark problems in order to compare different methods in different backflow regimes (with a full reversal flow and with propagating vortices after a stenosis). The examples are implemented in FreeFem++ and the source code is openly available, making them a solid basis for future method developments. -
P. Colli, G. Gilardi, J. Sprekels, On a Cahn--Hilliard system with convection and dynamic boundary conditions, Annali di Matematica Pura ed Applicata. Serie Quarta. Fondazione Annali di Matematica Pura ed Applicata, c/o Dipartimento di Matematica ``U. Dini'', Firenze; Springer-Verlag, Heidelberg. English, French, German, Italian, English abstracts., 197 (2018), pp. 1445--1475, DOI 10.1007/s10231-018-0732-1 .
Abstract
This paper deals with an initial and boundary value problem for a system coupling equation and boundary condition both of Cahn--Hilliard type; an additional convective term with a forced velocity field, which could act as a control on the system, is also present in the equation. Either regular or singular potentials are admitted in the bulk and on the boundary. Both the viscous and pure Cahn--Hilliard cases are investigated, and a number of results is proven about existence of solutions, uniqueness, regularity, continuous dependence, uniform boundedness of solutions, strict separation property. A complete approximation of the problem, based on the regularization of maximal monotone graphs and the use of a Faedo--Galerkin scheme, is introduced and rigorously discussed. -
G. Kitavtsev, A. Münch, B. Wagner, Thin film models for an active gel, Proceedings of The Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, 474 (2018), pp. 20170828/1--20170828/20, DOI 10.1098/rspa.2017.0828 .
-
M. Hintermüller, M. Hinze, Ch. Kahle, T. Keil, A goal-oriented dual-weighted adaptive finite element approach for the optimal control of a nonsmooth Cahn--Hilliard--Navier--Stokes system, Optimization and Engineering. International Multidisciplinary Journal to Promote Optimization Theory & Applications in Engineering Sciences, 19 (2018), pp. 629--662, DOI 10.1007/s11081-018-9393-6 .
Abstract
This paper is concerned with the development and implementation of an adaptive solution algorithm for the optimal control of a time-discrete Cahn--Hilliard--Navier--Stokes system with variable densities. The free energy density associated to the Cahn--Hilliard system incorporates the double-obstacle potential which yields an optimal control problem for a family of coupled systems in each time instant of a variational inequality of fourth order and the Navier--Stokes equation. A dual-weighed residual approach for goal-oriented adaptive finite elements is presented which is based on the concept of C-stationarity. The overall error representation depends on primal residual weighted by approximate dual quantities and vice versa as well as various complementary mismatch errors. Details on the numerical realization of the adaptive concept and a report on numerical tests are given. -
S. Bergmann, D.A. Barragan-Yani, E. Flegel, K. Albe, B. Wagner, Anisotropic solid-liquid interface kinetics in silicon: An atomistically informed phase-field model, Modelling and Simulation in Materials Science and Engineering, 25 (2017), pp. 065015/1--065015/20, DOI 10.1088/1361-651X/aa7862 .
Abstract
We present an atomistically informed parametrization of a phase-field model for describing the anisotropic mobility of liquid-solid interfaces in silicon. The model is derived from a consistent set of atomistic data and thus allows to directly link molecular dynamics and phase field simulations. Expressions for the free energy density, the interfacial energy and the temperature and orientation dependent interface mobility are systematically fitted to data from molecular dynamics simulations based on the Stillinger-Weber interatomic potential. The temperature-dependent interface velocity follows a Vogel-Fulcher type behavior and allows to properly account for the dynamics in the undercooled melt. -
W. Dreyer, C. Guhlke, Sharp limit of the viscous Cahn--Hilliard equation and thermodynamic consistency, Continuum Mechanics and Thermodynamics, 29 (2017), pp. 913--934.
Abstract
Diffuse and sharp interface models represent two alternatives to describe phase transitions with an interface between two coexisting phases. The two model classes can be independently formulated. Thus there arises the problem whether the sharp limit of the diffuse model fits into the setting of a corresponding sharp interface model. We call a diffuse model admissible if its sharp limit produces interfacial jump conditions that are consistent with the balance equations and the 2nd law of thermodynamics for sharp interfaces. We use special cases of the viscous Cahn-Hilliard equation to show that there are admissible as well as non-admissible diffuse interface models. -
M. Dziwnik, A. Münch, B. Wagner, An anisotropic phase-field model for solid-state dewetting and its sharp-interface limit, Nonlinearity, 30 (2017), pp. 1465--1496.
Abstract
We propose a phase field model for solid state dewetting in form of a Cahn-Hilliard equation with weakly anisotropic surface energy and a degenerate mobility together with a free boundary condition at the film-substrate contact line. We derive the corresponding sharp interface limit via matched asymptotic analysis involving multiple inner layers. The resulting sharp interface model is consistent with the pure surface diffusion model. In addition, we show that the natural boundary conditions, as indicated from the first variation of the total free energy, imply a contact angle condition for the dewetting front, which, in the isotropic case, is consistent with the well-known Young's equation. -
H. Antil, M. Hintermüller, R.H. Nochetto, Th.M. Surowiec, D. Wegner, Finite horizon model predictive control of electrowetting on dielectric with pinning, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 19 (2017), pp. 1--30, DOI 10.4171/IFB/375 .
-
P. Colli, G. Gilardi, E. Rocca, J. Sprekels, Optimal distributed control of a diffuse interface model of tumor growth, Nonlinearity, 30 (2017), pp. 2518--2546.
Abstract
In this paper, a distributed optimal control problem is studied for a diffuse interface model of tumor growth which was proposed by Hawkins--Daruud et al. in citeHZO. The model consists of a Cahn-Hilliard equation for the tumor cell fraction $vp$ coupled to a reaction-diffusion equation for a function $s$ representing the nutrient-rich extracellular water volume fraction. The distributed control $u$ monitors as a right-hand side the equation for $s$ and can be interpreted as a nutrient supply or a medication, while the cost function, which is of standard tracking type, is meant to keep the tumor cell fraction under control during the evolution. We show that the control-to-state operator is Fréchet differentiable between appropriate Banach spaces and derive the first-order necessary optimality conditions in terms of a variational inequality involving the adjoint state variables. -
P. Colli, G. Gilardi, E. Rocca, J. Sprekels, Asymptotic analyses and error estimates for a Cahn--Hilliard type phase field system modelling tumor growth, Discrete and Continuous Dynamical Systems, 10 (2017), pp. 37--54.
Abstract
This paper is concerned with a phase field system of Cahn--Hilliard type that is related to a tumor growth model and consists of three equations in gianni terms of the variables order parameter, chemical potential and nutrient concentration. This system has been investigated in the recent papers citeCGH and citeCGRS gianni from the viewpoint of well-posedness, long time bhv and asymptotic convergence as two positive viscosity coefficients tend to zero at the same time. Here, we continue the analysis performed in citeCGRS by showing two independent sets of results as just one of the coefficents tends to zero, the other remaining fixed. We prove convergence results, uniqueness of solutions to the two resulting limit problems, and suitable error estimates -
P. Krejčí, E. Rocca, J. Sprekels, Unsaturated deformable porous media flow with thermal phase transition, Mathematical Models & Methods in Applied Sciences, 27 (2017), pp. 2675--2710, DOI 10.1142/S0218202517500555 .
Abstract
In the present paper, a continuum model is introduced for fluid flow in a deformable porous medium, where the fluid may undergo phase transitions. Typically, such problems arise in modeling liquid-solid phase transformations in groundwater flows. The system of equations is derived here from the conservation principles for mass, momentum, and energy and from the Clausius-Duhem inequality for entropy. It couples the evolution of the displacement in the matrix material, of the capillary pressure, of the absolute temperature, and of the phase fraction. Mathematical results are proved under the additional hypothesis that inertia effects and shear stresses can be neglected. For the resulting highly nonlinear system of two PDEs, one ODE and one ordinary differential inclusion with natural initial and boundary conditions, existence of global in time solutions is proved by means of cut-off techniques and suitable Moser-type estimates. -
A. Münch, B. Wagner, L.P. Cook, R.R. Braun, Apparent slip for an upper convected Maxwell fluid, SIAM Journal on Applied Mathematics, 77 (2017), pp. 537--564, DOI 10.1137/16M1056869 .
Abstract
In this study the flow field of a nonlocal, diffusive upper convected Maxwell (UCM) fluid with a polymer in a solvent undergoing shearing motion is investigated for pressure driven planar channel flow and the free boundary problem of a liquid layer on a solid substrate. For large ratios of the zero shear polymer viscosity to the solvent viscosity, it is shown that channel flows exhibit boundary layers at the channel walls. In addition, for increasing stress diffusion the flow field away from the boundary layers undergoes a transition from a parabolic to a plug flow. Using experimental data for the wormlike micelle solutions CTAB/NaSal and CPyCl/NaSal, it is shown that the analytic solution of the governing equations predicts these signatures of the velocity profiles. Corresponding flow structures and transitions are found for the free boundary problem of a thin layer sheared along a solid substrate. Matched asymptotic expansions are used to first derive sharp-interface models describing the bulk flow with expressions for an em apparent slip for the boundary conditions, obtained by matching to the flow in the boundary layers. For a thin film geometry several asymptotic regimes are identified in terms of the order of magnitude of the stress diffusion, and corresponding new thin film models with a slip boundary condition are derived. -
J. Sprekels, E. Valdinoci, A new type of identification problems: Optimizing the fractional order in a nonlocal evolution equation, SIAM Journal on Control and Optimization, 55 (2017), pp. 70--93.
Abstract
In this paper, we consider a rather general linear evolution equation of fractional type, namely a diffusion type problem in which the diffusion operator is the power of a positive definite operator having a positive and discrete spectrum. We prove existence, uniqueness and differentiability properties with respect to the fractional parameter. These results are then employed to derive existence as well as first-order necessary and second-order sufficient optimality conditions for a minimization problem, which is inspired by considerations in mathematical biology. In this problem, the fractional parameter $s$ serves as the “control parameter” that needs to be chosen in such a way as to minimize a given cost functional. This problem constitutes a new classof identification problems: while usually in identification problems the type of the differential operator is prescribed and one or several of its coefficient functions need to be identified, in the present case one has to determine the type of the differential operator itself. This problem exhibits the inherent analytical difficulty that with changing fractional parameter also the domain of definition, and thus the underlying function space, of the fractional operator changes. -
M. Hintermüller, C.N. Rautenberg, On the uniqueness and numerical approximation of solutions to certain parabolic quasi-variational inequalities, Portugaliae Mathematica. A Journal of the Portuguese Mathematical Society, 74 (2017), pp. 1--35.
Abstract
A class of abstract nonlinear evolution quasi-variational inequality (QVI) problems in function space is considered. The abstract framework developed in this paper includes constraint sets of obstacle and gradient type. The paper address the existence, uniqueness and approximation of solutions when the constraint set mapping is of a special form. Uniqueness is addressed through contractive behavior of a nonlinear mapping whose fixed points are solutions to the QVI. An axiomatic semi-discrete approximation scheme is developed, which is proven to be convergent and which is numerically implemented. The paper ends by a report on numerical tests for several nonlinear constraints of gradient-type. -
E. Meca Álvarez, A. Münch, B. Wagner, Sharp-interface formation during lithium intercalation into silicon, European Journal of Applied Mathematics, 29 (2018), pp. 118--145, DOI 10.1017/S0956792517000067 .
Abstract
In this study we present a phase-field model that describes the process of intercalation of Li ions into a layer of an amorphous solid such as a-Si. The governing equations couple a viscous Cahn-Hilliard-Reaction model with elasticity in the framework of the Cahn-Larché system. We discuss the parameter settings and flux conditions at the free boundary that lead to the formation of phase boundaries having a sharp gradient in ion concentration between the initial state of the solid layer and the intercalated region. We carry out a matched asymptotic analysis to derive the corresponding sharp-interface model that also takes into account the dynamics of triple points where the sharp interface in the bulk of the layer intersects the free boundary. We numerically compare the interface motion predicted by the sharp-interface model with the long-time dynamics of the phase-field model. -
M. Cozzi, A. Farina, E. Valdinoci, Monotonicity formulae and classification results for singular, degenerate, anisotropic PDEs, Advances in Mathematics, 293 (2016), pp. 343--381.
Abstract
We consider possibly degenerate and singular elliptic equations in a possibly anisotropic medium. We obtain monotonicity results for the energy density, rigidity results for the solutions and classi?cation results for the singularity/degeneracy/anisotropy allowed. As far as we know, these results are new even in the case of non-singular and non- degenerate anisotropic equations. -
S.P. Frigeri, Global existence of weak solutions for a nonlocal model for two-phase flows of incompressible fluids with unmatched densities, Mathematical Models & Methods in Applied Sciences, 26 (2016), pp. 1957--1993.
Abstract
We consider a diffuse interface model for an incompressible isothermal mixture of two viscous Newtonian fluids with different densities in a bounded domain in two or three space dimensions. The model is the nonlocal version of the one recently derived by Abels, Garcke and Grün and consists of a Navier-Stokes type system coupled with a convective nonlocal Cahn-Hilliard equation. The density of the mixture depends on an order parameter. For this nonlocal system we prove existence of global dissipative weak solutions for the case of singular double-well potentials and non degenerate mobilities. To this goal we devise an approach which is completely independent of the one employed by Abels, Depner and Garcke to establish existence of weak solutions for the local Abels et al. model. -
M. Dai, E. Feireisl, E. Rocca, G. Schimperna, M.E. Schonbek, On asymptotic isotropy for a hydrodynamic model of liquid crystals, Asymptotic Analysis, 97 (2016), pp. 189--210.
Abstract
We study a PDE system describing the motion of liquid crystals by means of the Q?tensor description for the crystals coupled with the incompressible Navier-Stokes system. Using the method of Fourier splitting, we show that solutions of the system tend to the isotropic state at the rate (1 + t)?? as t ? ? 1 for a certain ? > 2 . -
S. Dipierro, O. Savin, E. Valdinoci, Graph properties for nonlocal minimal surfaces, Calculus of Variations and Partial Differential Equations, 55 (2016), pp. 86/1--86/25.
Abstract
In this paper we show that a nonlocal minimal surface which is a graph outside a cylinder is in fact a graph in the whole of the space. As a consequence, in dimension 3, we show that the graph is smooth. The proofs rely on convolution techniques and appropriate integral estimates which show the pointwise validity of an Euler?Lagrange equation related to the nonlocal mean curvature. -
S. Patrizi, E. Valdinoci, Relaxation times for atom dislocations in crystals, Calculus of Variations and Partial Differential Equations, 55 (2016), pp. 71/1--71/44.
Abstract
We study the relaxation times for a parabolic differential equation whose solution represents the atom dislocation in a crystal. The equation that we consider comprises the classical Peierls?Nabarro model as a particular case, and it allows also long range interactions. It is known that the dislocation function of such a model has the tendency to concentrate at single points, which evolve in time according to the external stress and a singular, long range potential. Depending on the orientation of the dislocation function at these points, the potential may be either attractive or repulsive, hence collisions may occur in the latter case and, at the collision time, the dislocation function does not disappear. The goal of this paper is to provide accurate estimates on the relaxation times of the system after collision. More precisely, we take into account the case of two and three colliding points, and we show that, after a small transition time subsequent to the collision, the dislocation function relaxes exponentially fast to a steady state. In this sense, the system exhibits two different decay behaviors, namely an exponential time decay versus a polynomial decay in the space variables (and these two homogeneities are kept separate during the time evolution). -
A. Farina, E. Valdinoci, 1D symmetry for semilinear PDEs from the limit interface of the solution, Communications in Partial Differential Equations, 41 (2016), pp. 665--682.
Abstract
We study bounded, monotone solutions of ?u = W?(u) in the whole of ?n, where W is a double-well potential. We prove that under suitable assumptions on the limit interface and on the energy growth, u is 1D. In particular, differently from the previous literature, the solution is not assumed to have minimal properties and the cases studied lie outside the range of ?-convergence methods. We think that this approach could be fruitful in concrete situations, where one can observe the phase separation at a large scale and wishes to deduce the values of the state parameter in the vicinity of the interface. As a simple example of the results obtained with this point of view, we mention that monotone solutions with energy bounds, whose limit interface does not contain a vertical line through the origin, are 1D, at least up to dimension 4. -
M. Korzec, A. Münch, E. Süli, B. Wagner, Anisotropy in wavelet based phase field models, Discrete and Continuous Dynamical Systems. Series B. A Journal Bridging Mathematics and Sciences, 21 (2016), pp. 1167--1187.
Abstract
Anisotropy is an essential feature of phase-field models, in particular when describing the evolution of microstructures in solids. The symmetries of the crystalline phases are reflected in the interfacial energy by introducing corresponding directional dependencies in the gradient energy coefficients, which multiply the highest order derivative in the phase-field model. This paper instead considers an alternative approach, where the anisotropic gradient energy terms are replaced by a wavelet analogue that is intrinsically anisotropic and linear. In our studies we focus on the classical coupled temperature - Ginzburg-Landau type phase-field model for dendritic growth. For the resulting derivative-free wavelet analogue existence, uniqueness and continuous dependence on initial data for weak solutions is proved. The ability to capture dendritic growth similar to the results obtained from classical models is investigated numerically. -
W. Dreyer, C. Guhlke, R. Müller, A new perspective on the electron transfer: Recovering the Butler--Volmer equation in non-equilibrium thermodynamics, Physical Chemistry Chemical Physics, 18 (2016), pp. 24966--24983, DOI 10.1039/C6CP04142F .
Abstract
Understanding and correct mathematical description of electron transfer reaction is a central question in electrochemistry. Typically the electron transfer reactions are described by the Butler-Volmer equation which has its origin in kinetic theories. The Butler-Volmer equation relates interfacial reaction rates to bulk quantities like the electrostatic potential and electrolyte concentrations. Since in the classical form, the validity of the Butler-Volmer equation is limited to some simple electrochemical systems, many attempts have been made to generalize the Butler-Volmer equation. Based on non-equilibrium thermodynamics we have recently derived a reduced model for the electrode-electrolyte interface. This reduced model includes surface reactions but does not resolve the charge layer at the interface. Instead it is locally electroneutral and consistently incorporates all features of the double layer into a set of interface conditions. In the context of this reduced model we are able to derive a general Butler-Volmer equation. We discuss the application of the new Butler-Volmer equations to different scenarios like electron transfer reactions at metal electrodes, the intercalation process in lithium-iron-phosphate electrodes and adsorption processes. We illustrate the theory by an example of electroplating. -
S.P. Frigeri, E. Rocca, J. Sprekels, Optimal distributed control of a nonlocal Cahn--Hilliard/Navier--Stokes system in two dimensions, SIAM Journal on Control and Optimization, 54 (2016), pp. 221 -- 250.
Abstract
We study a diffuse interface model for incompressible isothermal mixtures of two immiscible fluids coupling the Navier-Stokes system with a convective nonlocal Cahn-Hilliard equation in two dimensions of space. We apply recently proved well-posedness and regularity results in order to establish existence of optimal controls as well as first-order necessary optimality conditions for an associated optimal control problem in which a distributed control is applied to the fluid flow. -
M. Hintermüller, S. Rösel, A duality-based path-following semismooth Newton method for elasto-plastic contact problems, Journal of Computational and Applied Mathematics, 292 (2016), pp. 150--173.
-
M. Hintermüller, Th. Surowiec, A bundle-free implicit programming approach for a class of elliptic MPECs in function space, Mathematical Programming Series A, 160 (2016), pp. 271--305.
-
S. Patrizi, E. Valdinoci, Crystal dislocations with different orientations and collisions, Archive for Rational Mechanics and Analysis, 217 (2015), pp. 231--261.
Abstract
We study a parabolic differential equation whose solution represents the atom dislocation in a crystal for a general type of Peierls-Nabarro model with possibly long range interactions and an external stress. Differently from the previous literature, we treat here the case in which such dislocation is not the superpositions of transitions all occurring with the same orientations (i.e. opposite orientations are allowed as well). We show that, at a long time scale, and at a macroscopic space scale, the dislocations have the tendency to concentrate as pure jumps at points which evolve in time, driven by the external stress and by a singular potential. Due to differences in the dislocation orientations, these points may collide in finite time. -
E. Rocca, R. Rossi, ``Entropic'' solutions to a thermodynamically consistent PDE system for phase transitions and damage, SIAM Journal on Mathematical Analysis, 74 (2015), pp. 2519--2586.
Abstract
In this paper we analyze a PDE system modelling (non-isothermal) phase transitions and dam- age phenomena in thermoviscoelastic materials. The model is thermodynamically consistent: in particular, no small perturbation assumption is adopted, which results in the presence of quadratic terms on the right-hand side of the temperature equation, only estimated in L^1. The whole system has a highly nonlinear character. We address the existence of a weak notion of solution, referred to as “entropic”, where the temperature equation is formulated with the aid of an entropy inequality, and of a total energy inequality. This solvability concept reflects the basic principles of thermomechanics as well as the thermodynamical consistency of the model. It allows us to obtain global-in-time existence theorems without imposing any restriction on the size of the initial data. We prove our results by passing to the limit in a time discretization scheme, carefully tailored to the nonlinear features of the PDE system (with its “entropic” formulation), and of the a priori estimates performed on it. Our time-discrete analysis could be useful towards the numerical study of this model. -
P.-É. Druet, Higher $L^p$ regularity for vector fields that satisfy divergence and rotation constraints in dual Sobolev spaces, and application to some low-frequency Maxwell equations, Discrete and Continuous Dynamical Systems, 8 (2015), pp. 479--496.
Abstract
We show that Lp vector fields over a Lipschitz domain are integrable to higher exponents if their generalized divergence and rotation can be identified with bounded linear operators acting on standard Sobolev spaces. A Div-Curl Lemma-type argument provides compact embedding results for such vector fields. We investigate the regularity of the solution fields for the low-frequency approximation of the Maxwell equations in time-harmonic regime. We focus on the weak formulation 'in H' of the problem, in a reference geometrical setting allowing for material heterogeneities. -
P.-É. Druet, Some mathematical problems related to the second order optimal shape of a crystallization interface, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 2443--2463.
Abstract
We consider the problem to optimize the stationary temperature distribution and the equilibrium shape of the solid-liquid interface in a two-phase system subject to a temperature gradient. The interface satisfies the minimization principle of the free energy, while the temperature is solving the heat equation with a radiation boundary conditions at the outer wall. Under the condition that the temperature gradient is uniformly negative in the direction of crystallization, the interface is expected to have a global graph representation. We reformulate this condition as a pointwise constraint on the gradient of the state, and we derive the first order optimality system for a class of objective functionals that account for the second surface derivatives, and for the surface temperature gradient. -
S.P. Frigeri, M. Grasselli, E. Rocca, A diffuse interface model for two-phase incompressible flows with nonlocal interactions and nonconstant mobility, Nonlinearity, 28 (2015), pp. 1257--1293.
Abstract
We consider a diffuse interface model for incompressible isothermal mixtures of two immiscible fluids with matched constant densities. This model consists of the Navier-Stokes system coupled with a convective nonlocal Cahn-Hilliard equation with non-constant mobility. We first prove the existence of a global weak solution in the case of non-degenerate mobilities and regular potentials of polynomial growth. Then we extend the result to degenerate mobilities and singular (e.g. logarithmic) potentials. In the latter case we also establish the existence of the global attractor in dimension two. Using a similar technique, we show that there is a global attractor for the convective nonlocal Cahn-Hilliard equation with degenerate mobility and singular potential in dimension three. -
D. Peschka, Thin-film free boundary problems for partial wetting, Journal of Computational Physics, 295 (2015), pp. 770--778.
Abstract
We present a novel framework to solve thin-film equations with an explicit non-zero contact angle, where the support of the solution is treated as an unknown. The algorithm uses a finite element method based on a gradient formulation of the thin-film equations coupled to an arbitrary Lagrangian-Eulerian method for the motion of the support. Features of this algorithm are its simplicity and robustness. We apply this algorithm in 1D and 2D to problems with surface tension, contact angles and with gravity. -
A. Di Castro, M. Novaga, R. Berardo, E. Valdinoci, Nonlocal quantitative isoperimetric inequalities, Calculus of Variations and Partial Differential Equations, 54 (2015), pp. 2421--2464.
-
S. Dipierro, E. Valdinoci, On a fractional harmonic replacement, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 3377--3392.
Abstract
Given $s ∈(0,1)$, we consider the problem of minimizing the Gagliardo seminorm in $H^s$ with prescribed condition outside the ball and under the further constraint of attaining zero value in a given set $K$. We investigate how the energy changes in dependence of such set. In particular, under mild regularity conditions, we show that adding a set $A$ to $K$ increases the energy of at most the measure of $A$ (this may be seen as a perturbation result for small sets $A$). Also, we point out a monotonicity feature of the energy with respect to the prescribed sets and the boundary conditions. -
S. Dipierro, O. Savin, E. Valdinoci, A nonlocal free boundary problem, SIAM Journal on Mathematical Analysis, 47 (2015), pp. 4559--4605.
Abstract
We consider a nonlocal free boundary problem built by a fractional Dirichlet norm plus a fractional perimeter. Among other results, we prove a monotonicity formula for the minimizers, glueing lemmata, uniform energy bounds, convergence results, a regularity theory for the planar cones and a trivialization result for the flat case. Several classical free boundary problems are limit cases of the one that we consider in this paper. -
R. Servadei, E. Valdinoci, The Brezis--Nirenberg result for the fractional Laplacian, Transactions of the American Mathematical Society, 367 (2015), pp. 67--102.
-
L. Caffarelli, O. Savin , E. Valdinoci, Minimization of a fractional perimeter-Dirichlet integral functional, Annales de l'Institut Henri Poincare. Analyse Non Lineaire, 32 (2015), pp. 901--924.
-
J. Dávila, M. Del Pino, S. Dipierro, E. Valdinoci, Concentration phenomena for the nonlocal Schrödinger equation with Dirichlet datum, Analysis & PDE, 8 (2015), pp. 1165--1235.
Abstract
For a smooth, bounded Euclidean domain, we consider a nonlocal Schrödinger equation with zero Dirichlet datum. We construct a family of solutions that concentrate at an interior point of the domain in the form of a scaling of the ground state in entire space. Unlike the classical case, the leading order of the associated reduced energy functional in a variational reduction procedure is of polynomial instead of exponential order on the distance from the boundary, due to the nonlocal effect. Delicate analysis is needed to overcome the lack of localization, in particular establishing the rather unexpected asymptotics for the Green function in the expanding domain. -
M.M. Fall, F. Mahmoudi, E. Valdinoci, Ground states and concentration phenomena for the fractional Schrödinger equation, Nonlinearity, 28 (2015), pp. 1937--1961.
Abstract
We consider here solutions of the nonlinear fractional Schrödinger equation. We show that concentration points must be critical points for the potential. We also prove that, if the potential is coercive and has a unique global minimum, then ground states concentrate suitably at such minimal point. In addition, if the potential is radial, then the minimizer is unique. -
E. Feireisl, E. Rocca, G. Schimperna, A. Zarnescu, Nonisothermal nematic liquid crystal flows with the Ball--Majumdar free energy, Annali di Matematica Pura ed Applicata. Serie Quarta. Fondazione Annali di Matematica Pura ed Applicata, c/o Dipartimento di Matematica ``U. Dini'', Firenze; Springer-Verlag, Heidelberg. English, French, German, Italian, English abstracts., 194 (2015), pp. 1269--1299.
Abstract
In this paper we prove the existence of global in time weak solutions for an evolutionary PDE system modelling nonisothermal Landau-de Gennes nematic liquid crystal (LC) flows in three dimensions of space. In our model, the incompressible Navier-Stokes system for the macroscopic velocity $vu$ is coupled to a nonlinear convective parabolic equation describing the evolution of the Q-tensor $QQ$, namely a tensor-valued variable representing the normalized second order moments of the probability distribution function of the LC molecules. The effects of the (absolute) temperature $vt$ are prescribed in the form of an energy balance identity complemented with a global entropy production inequality. Compared to previous contributions, we can consider here the physically realistic singular configuration potential $f$ introduced by Ball and Majumdar. This potential gives rise to severe mathematical difficulties since it introduces, in the Q-tensor equation, a term which is at the same time singular in $QQ$ and degenerate in $vt$. To treat it a careful analysis of the properties of $f$, particularly of its blow-up rate, is carried out. -
A. Fiscella, R. Servadei, E. Valdinoci, Asymptotically linear problems driven by fractional Laplacian operators, Mathematical Methods in the Applied Sciences, 38 (2015), pp. 3551--3563.
Abstract
In this paper we study a non-local fractional Laplace equation, depending on a parameter, with asymptotically linear right-hand side. Our main result concerns the existence of weak solutions for this equation and it is obtained using variational and topological methods. We treat both the nonresonant case and the resonant one. -
D.A. Gomes, S. Patrizi, Obstacle mean-field game problem, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 17 (2015), pp. 55--68.
Abstract
In this paper, we introduce and study a first-order mean-field game obstacle problem. We examine the case of local dependence on the measure under assumptions that include both the logarithmic case and power-like nonlinearities. Since the obstacle operator is not differentiable, the equations for first-order mean field game problems have to be discussed carefully. Hence, we begin by considering a penalized problem. We prove this problem admits a unique solution satisfying uniform bounds. These bounds serve to pass to the limit in the penalized problem and to characterize the limiting equations. Finally, we prove uniqueness of solutions. -
M.G. Hennessy, V.M. Burlakov, A. Münch, B. Wagner, A. Goriely, Controlled topological transitions in thin-film phase separation, SIAM Journal on Applied Mathematics, 75 (2015), pp. 38--60.
Abstract
In this paper the evolution of a binary mixture in a thin-film geometry with a wall at the top and bottom is considered. Bringing the mixture into its miscibility gap so that no spinodal decomposition occurs in the bulk, a slight energetic bias of the walls towards each one of the constituents ensures the nucleation of thin boundary layers that grow until the constituents have moved into one of the two layers. These layers are separated by an interfacial region, where the composition changes rapidly. Conditions that ensure the separation into two layers with a thin interfacial region are investigated based on a phase-field model and using matched asymptotic expansions a corresponding sharp-interface problem for the location of the interface is established. It is then argued that a thus created two-layer system is not at its energetic minimum but destabilizes into a controlled self-replicating pattern of trapezoidal vertical stripes by minimizing the interfacial energy between the phases while conserving their area. A quantitative analysis of this mechanism is carried out via a new thin-film model for the free interfaces, which is derived asymptotically from the sharp-interface model. -
R. Huth, S. Jachalski, G. Kitavtsev, D. Peschka, Gradient flow perspective on thin-film bilayer flows, Journal of Engineering Mathematics, 94 (2015), pp. 43--61.
Abstract
We study gradient flow formulations of thin-film bilayer flows with triple-junctions between liquid/liquid/air. First we highlight the gradient structure in the Stokes free-boundary flow and identify its solutions with the well known PDE with boundary conditions. Next we propose a similar gradient formulation for the corresponding thin-film model and formally identify solutions with those of the corresponding free-boundary problem. A robust numerical algorithm for the thin-film gradient flow structure is then provided. Using this algorithm we compare the sharp triple-junction model with precursor models. For their stationary solutions a rigorous connection is established using Gamma-convergence. For time-dependent solutions the comparison of numerical solutions shows a good agreement for small and moderate times. Finally we study spreading in the zero-contact angle case, where we compare numerical solutions with asymptotically exact source-type solutions. -
F. Punzo, E. Valdinoci, Uniqueness in weighted Lebesgue spaces for a class of fractional parabolic and elliptic equations, Journal of Differential Equations, 258 (2015), pp. 555--587.
-
E. Rocca, R. Rossi, A degenerating PDE system for phase transitions and damage, Mathematical Models & Methods in Applied Sciences, 24 (2014), pp. 1265--1341.
-
G. Aki, W. Dreyer, J. Giesselmann, Ch. Kraus, A quasi-incompressible diffuse interface model with phase transition, Mathematical Models & Methods in Applied Sciences, 24 (2014), pp. 827--861.
Abstract
This work introduces a new thermodynamically consistent diffuse model for two-component flows of incompressible fluids. For the introduced diffuse interface model, we investigate physically admissible sharp interface limits by matched asymptotic techniques. To this end, we consider two scaling regimes where in one case we recover the Euler equations and in the other case the Navier-Stokes equations in the bulk phases equipped with admissible interfacial conditions. For the Navier-Stokes regime, we further assume the densities of the fluids are close to each other in the sense of a small parameter which is related to the interfacial thickness of the diffuse model. -
B. Barrios, I. Peral, F. Soria, E. Valdinoci, A Widder's type theorem for the heat equation with nonlocal diffusion, Archive for Rational Mechanics and Analysis, 213 (2014), pp. 629--650.
-
L. Blank, M.H. Farshbaf Shaker, H. Garcke, V. Styles, Relating phase field and sharp interface approaches to structural topology optimization, ESAIM. Control, Optimisation and Calculus of Variations, 20 (2014), pp. 1025--1058.
Abstract
A phase field approach for structural topology optimization which allows for topology changes and multiple materials is analyzed. First order optimality conditions are rigorously derived and it is shown via formally matched asymptotic expansions that these conditions converge to classical first order conditions obtained in the context of shape calculus. We also discuss how to deal with triple junctions where e.g. two materials and the void meet. Finally, we present several numerical results for mean compliance problems and a cost involving the least square error to a target displacement. -
A. Cesaroni, M. Novaga, E. Valdinoci, A symmetry result for the Ornstein--Uhlenbeck operator, Discrete and Continuous Dynamical Systems, 34 (2014), pp. 2451--2467.
-
R. Servadei, E. Valdinoci, On the spectrum of two different fractional operators, Proceedings of the Royal Society of Edinburgh. Section A. Mathematics, 144 (2014), pp. 831--855.
-
N. Abatangelo, E. Valdinoci, A notion of nonlocal curvature, Numerical Functional Analysis and Optimization. An International Journal, 35 (2014), pp. 793--815.
-
C. Bertoglio, A. Caiazzo, A tangential regularization method for backflow stabilization in hemodynamics, Journal of Computational Physics, 261 (2014), pp. 162--171.
Abstract
In computational simulations of fluid flows, instabilities at the Neumann boundaries may appear during backflow regime. It is widely accepted that this is due to the incoming energy at the boundary, coming from the convection term, which cannot be controlled when the velocity field is unknown. We propose a stabilized formulation based on a local regularization of the fluid velocity along the tangential directions on the Neumann boundaries. The stabilization term is proportional to the amount of backflow, and does not require any further assumption on the velocity profile. The perfomance of the method is assessed on a two- and three-dimensional Womersley flows, as well as considering a hemodynamic physiological regime in a patient-specific aortic geometry. -
M. Cozzi, A. Farina, E. Valdinoci, Gradient bounds and rigidity results for singular, degenerate, anisotropic partial differential equations, Communications in Mathematical Physics, 331 (2014), pp. 189--214.
-
M.M. Fall, E. Valdinoci, Uniqueness and nondegeneracy of positive solutions of (-Delta) su+u=up in RN when s is close to 1, Communications in Mathematical Physics, 329 (2014), pp. 383--404.
-
A. Farina, E. Valdinoci, Gradient bounds for anisotropic partial differential equations, Calculus of Variations and Partial Differential Equations, 49 (2014), pp. 923--936.
-
A. Fiscella, E. Valdinoci, A critical Kirchhoff type problem involving a nonlocal operator, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 94 (2014), pp. 156--170.
-
S. Melchionna, E. Rocca, On a nonlocal Cahn--Hilliard equation with a reaction term, Advances in Mathematical Sciences and Applications, 24 (2014), pp. 461--497.
Abstract
We prove existence, uniqueness, regularity and separation properties for a nonlocal Cahn- Hilliard equation with a reaction term. We deal here with the case of logarithmic potential and degenerate mobility as well an uniformly lipschitz in u reaction term g(x, t, u). -
A. Miranville, E. Rocca, G. Schimperna, A. Segatti, The Penrose--Fife phase-field model with coupled dynamic boundary conditions, Discrete and Continuous Dynamical Systems, 34 (2014), pp. 4259--4290.
-
O. Savin, E. Valdinoci, Density estimates for a variational model driven by the Gagliardo norm, Journal de Mathématiques Pures et Appliquées, 101 (2014), pp. 1--26.
-
D.A. Gomes, S. Patrizi, V. Voskanyan, On the existence of classical solutions for stationary extended mean field games, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 99 (2014), pp. 49--79.
-
P.-É. Druet, Global Lipschitz continuity for elliptic transmission problems with a boundary intersecting interface, Mathematica Bohemica, 138 (2013), pp. 185--224.
Abstract
We investigate the regularity of the weak solution to elliptic transmission problems that involve two layered anisotropic materials separated by a boundary intersecting interface. Under a compatibility condition for the angle of contact of the two surfaces and the boundary data, we prove the existence of square-integrable second derivatives, and the global Lipschitz continuity of the solution. We show that the second weak derivatives remain integrable to a certain power less than two if the compatibility condition is violated. -
A. Farina, E. Valdinoci, On partially and globally overdetermined problems of elliptic type, American Journal of Mathematics, 135 (2013), pp. 1699--1726.
-
P.-E. Druet, The classical solvability of the contact angle problem for generalized equations of mean curvature type, Portugaliae Mathematica. A Journal of the Portuguese Mathematical Society, 69 (2012), pp. 233--258.
Abstract
In this paper, mean curvature type equations with general potentials and contact angle boundary conditions are considered. We extend the ideas of Ural'tseva, formulating sharper hypotheses for the existence of a classical solution. Corner stone for these results is a method to estimate quantities on the boundary of the free surface. We moreover provide alternative proofs for the higher-order estimates, and for the existence result. -
D. Knees, A. Schröder, Global spatial regularity for elasticity models with cracks, contact and other nonsmooth constraints, Mathematical Methods in the Applied Sciences, 35 (2012), pp. 1859--1884.
Abstract
A global higher differentiability result in Besov spaces is proved for the displacement fields of linear elastic models with self contact. Domains with cracks are studied, where nonpenetration conditions/Signorini conditions are imposed on the crack faces. It is shown that in a neighborhood of crack tips (in 2D) or crack fronts (3D) the displacement fields are B 3/2 2,∞ regular. The proof relies on a difference quotient argument for the directions tangential to the crack. In order to obtain the regularity estimates also in the normal direction, an argument due to Ebmeyer/Frehse/Kassmann is modified. The methods are then applied to further examples like contact problems with nonsmooth rigid foundations, to a model with Tresca friction and to minimization problems with nonsmooth energies and constraints as they occur for instance in the modeling of shape memory alloys. Based on Falk's approximation Theorem for variational inequalities, convergence rates for FE-discretizations of contact problems are derived relying on the proven regularity properties. Several numerical examples illustrate the theoretical results. -
P.-É. Druet, O. Klein, J. Sprekels, F. Tröltzsch, I. Yousept, Optimal control of three-dimensional state-constrained induction heating problems with nonlocal radiation effects, SIAM Journal on Control and Optimization, 49 (2011), pp. 1707--1736.
Abstract
The paper is concerned with a class of optimal heating problems in semiconductor single crystal growth processes. To model the heating process, time-harmonic Maxwell equations are considered in the system of the state. Due to the high temperatures characterizing crystal growth, it is necessary to include nonlocal radiation boundary conditions and a temperature-dependent heat conductivity in the description of the heat transfer process. The first goal of this paper is to prove the existence and uniqueness of the solution to the state equation. The regularity analysis associated with the time harmonic Maxwell equations is also studied. In the second part of the paper, the existence and uniqueness of the solution to the corresponding linearized equation is shown. With this result at hand, the differentiability of the control-to-state mapping operator associated with the state equation is derived. Finally, based on the theoretical results, first oder necessary optimality conditions for an associated optimal control problem are established. -
K. Kostourou, D. Peschka, A. Münch, B. Wagner, S. Herminghaus, R. Seemann, Interface morphologies in liquid/liquid dewetting, Chemical Engineering and Processing, 50 (2011), pp. 531--536.
Abstract
The dynamics and morphology of a liquid polystyrene (PS) film on the scale of a hundred nanometer dewetting from a liquid polymethylmethacrylate (PMMA) film is investigated experimentally and theoretically. The polymers considered here are both below their entanglement lengths and have negligible elastic properties. A theoretical model based on viscous Newtonian flow for both polymers is set up from which a system of coupled lubrication equations is derived and solved numerically. A direct comparison of the numerical solution with the experimental findings for the characteristic signatures of the cross-sections of liquid/air and liquid/liquid phase boundaries of the dewetting rims as well as the dewetting rates is performed and discussed for various viscosity ratios of the PS and PMMA layers. -
CH. Kraus, The degenerate and non-degenerate Stefan problem with inhomogeneous and anisotropic Gibbs--Thomson law, European Journal of Applied Mathematics, 22 (2011), pp. 393--422.
Abstract
The Stefan problem is coupled with a spatially inhomogeneous and anisotropic Gibbs-Thomson condition at the phase boundary. We show the long-time existence of weak solutions for the non-degenerate Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law and a conditional existence result for the corresponding degenerate Stefan problem. To this end approximate solutions are constructed by means of variational functionals with spatially inhomogeneous and anisotropic interfacial energy. By passing to the limit, we establish solutions of the Stefan problem with a spatially inhomogeneous and anisotropic Gibbs-Thomson law in a weak generalized BV-formulation. -
D. Peschka, A. Münch, B. Niethammer, Self-similar rupture of viscous thin films in the strong-slip regime, Nonlinearity, 23 (2010), pp. 409--427.
Abstract
We consider rupture of thin viscous films in the strong-slip regime with small Reynolds numbers. Numerical simulations indicate that near the rupture point viscosity and van-der-Waals forces are dominant and that there are self-similar solutions of the second kind. For a corresponding simplified model we rigorously analyse self-similar behaviour. There exists a one-parameter family of self-similar solutions and we establish necessary and sufficient conditions for convergence to any self-similar solution in a certain parameter regime. We also present a conjecture on the domains of attraction of all self-similar solutions which is supported by numerical simulations. -
P. Krejčí, E. Rocca, J. Sprekels, A bottle in a freezer, SIAM Journal on Mathematical Analysis, 41 (2009), pp. 1851-1873.
-
O. Klein, F. Luterotti, R. Rossi, Existence and asymptotic analysis of a phase field model for supercooling, Quarterly of Applied Mathematics, 64 (2006), pp. 291-319.
-
W. Dreyer, B. Wagner, Sharp-interface model for eutectic alloys. Part I: Concentration dependent surface tension, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 7 (2005), pp. 199--227.
-
O. Klein, P. Philip, J. Sprekels, Modeling and simulation of sublimation growth of SiC bulk single crystals, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 6 (2004), pp. 295--314.
-
O. Klein, P. Philip, J. Sprekels, K. Wilmanski, Radiation- and convection-driven transient heat transfer during sublimation growth of silicon carbide single crystals, Journal of Crystal Growth, 222 (2001), pp. 832--851.
-
W. Dreyer, W.H. Müller, A study of the coarsening in tin/lead solders, International Journal of Solids and Structures, 37 (2000), pp. 3841--3871.
 Contributions to Collected Editions
Contributions to Collected Editions
-
A. Alphonse, M. Hintermüller, C.N. Rautenberg, Stability and sensitivity analysis for quasi-variational inequalities, in: Non-Smooth and Complementarity-Based Distributed Parameter Systems: Simulation and Hierarchical Optimization, M. Hintermüller, R. Herzog, Ch. Kanzow, M. Ulbrich, S. Ulbrich, eds., 172 of International Series of Numerical Mathematics, Birkhäuser, Springer Nature Switzerland AG, Cham, 2022, pp. 183--210.
-
D. Gahururu, M. Hintermüller, S.-M. Stengl, Th.M. Surowiec, Generalized Nash equilibrium problems with partial differential operators: Theory, algorithms and risk aversion, in: Non-Smooth and Complementarity-Based Distributed Parameter Systems: Simulation and Hierarchical Optimization, M. Hintermüller, R. Herzog, Ch. Kanzow, M. Ulbrich, S. Ulbrich, eds., 172 of International Series of Numerical Mathematics, Birkhäuser, Springer Nature Switzerland AG, Cham, 2022, pp. 145--181.
-
C. Grässle, M. Hintermüller, M. Hinze, T. Keil, Simulation and control of a nonsmooth Cahn--Hilliard Navier--Stokes system with variable fluid densities, in: Non-Smooth and Complementarity-Based Distributed Parameter Systems: Simulation and Hierarchical Optimization, M. Hintermüller, R. Herzog, Ch. Kanzow, M. Ulbrich, S. Ulbrich, eds., 172 of International Series of Numerical Mathematics, Birkhäuser, Springer Nature Switzerland AG, Cham, 2022, pp. 211--240.
-
R. Rossi, U. Stefanelli, M. Thomas, Rate-independent evolution of sets, in: Analysis of Evolutionary and Complex Systems: Issue on the Occasion of Alexander Mielke's 60th Birthday, M. Liero, S. Reichelt, G. Schneider, F. Theil, M. Thomas, eds., 14 of Discrete and Continuous Dynamical Systems -- Series S, American Institute of Mathematical Sciences, Springfield, 2021, pp. 89--119, DOI 10.3934/dcdss.2020304 .
Abstract
The goal of this work is to analyze a model for the rate-independent evolution of sets with finite perimeter. The evolution of the admissible sets is driven by that of (the complement of) a given time-dependent set, which has to include the admissible sets and hence is to be understood as an external loading. The process is driven by the competition between perimeter minimization and minimization of volume changes.In the mathematical modeling of this process, we distinguish the adhesive case, in which the constraint that the (complement of) the `external load' contains the evolving sets is penalized by a term contributing to the driving energy functional, from the brittle case, enforcing this constraint. The existence of Energetic solutions for the adhesive system is proved by passing to the limit in the associated time-incremental minimization scheme. In the brittle case, this time-discretization procedure gives rise to evolving sets satisfying the stability condition, but it remains an open problem to additionally deduce energy-dissipation balance in the time-continuous limit. This can be obtained under some suitable quantification of data. The properties of the brittle evolution law are illustrated by numerical examples in two space dimensions. -
D. Peschka, M. Thomas, T. Ahnert, A. Münch, B. Wagner, Gradient structures for flows of concentrated suspensions, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 295--318, DOI 10.1007/978-3-030-33116-0 .
Abstract
In this work we investigate a two-phase model for concentrated suspensions. We construct a PDE formulation using a gradient flow structure featuring dissipative coupling between fluid and solid phase as well as different driving forces. Our construction is based on the concept of flow maps that also allows it to account for flows in moving domains with free boundaries. The major difference compared to similar existing approaches is the incorporation of a non-smooth two-homogeneous term to the dissipation potential, which creates a normal pressure even for pure shear flows. -
D. Peschka, Numerics of contact line motion for thin films, in: 8th Vienna International Conference on Mathematical Modelling -- MATHMOD 2015, 48 of IFAC-PapersOnLine, Elsevier, 2015, pp. 390--393.
-
M.H. Farshbaf Shaker, T. Fukao, N. Yamazaki, Singular limit of Allen--Cahn equation with constraints and its Lagrange multiplier, in: Dynamical Systems, Differential Equations and Applications, AIMS Proceedings 2015, Proceedings of the 10th AIMS International Conference (Madrid, Spain), M. DE León, W. Feng, Z. Feng, X. Lu, J.M. Martell, J. Parcet, D. Peralta-Salas, W. Ruan, eds., AIMS Proceedings, American Institute of Mathematical Sciences, 2015, pp. 418--427.
Abstract
We consider the Allen-Cahn equation with constraint. Our constraint is the subdifferential of the indicator function on the closed interval, which is the multivalued function. In this paper we give the characterization of the Lagrange multiplier to our equation. Moreover, we consider the singular limit of our system and clarify the limit of the solution and the Lagrange multiplier to our problem. -
L. Blank, M.H. Farshbaf Shaker, C. Hecht, J. Michl, Ch. Rupprecht, Optimal control of Allen--Cahn systems, in: Trends in PDE Constrained Optimization, G. Leugering, P. Benner ET AL., eds., 165 of International Series of Numerical Mathematics, Birkhäuser, Basel et al., 2014, pp. 11--26.
-
L. Blank, M.H. Farshbaf Shaker, H. Garcke, Ch. Rupprecht, V. Styles, Multi-material phase field approach to structural topology optimization, in: Trends in PDE Constrained Optimization, G. Leugering, P. Benner ET AL., eds., 165 of International Series of Numerical Mathematics, Birkhäuser, Basel et al., 2014, pp. 231--246.
-
P. Rudolph, Ch. Frank-Rotsch, F.-M. Kiessling, W. Miller, U. Rehse, O. Klein, Ch. Lechner, J. Sprekels, B. Nacke, H. Kasjanov, P. Lange, M. Ziem, B. Lux, M. Czupalla, O. Root, V. Trautmann, G. Bethin, Crystal growth in heater-magnet modules --- From concept to use, in: Proceedings of the International Scientific Colloquium Modelling for Electromagnetic Processing (MEP2008), Hannover, October 26--29, 2008, E. Braake, B. Nacke, eds., Leibniz University of Hannover, 2008, pp. 79-84.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
M. Landstorfer, Ch. Pohl, F. Brosa Planella, K. Manmi, A model for SEI-growth based on non-equilibrium thermodynamics, Preprint no. 3250, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3250 .
Abstract, PDF (1092 kByte)
The growth of the solid electrolyte interphase (SEI) is a dominant degradation mechanism in lithium-ion batteries, governing capacity fade, coulombic efficiency, and long-term performance. Despite extensive experimental investigation, quantitative understanding of SEI formation and evolution remains limited by its nanoscale thickness, complex chemistry, and strong sensitivity to operating conditions. Existing zero-dimensional models capture individual rate-limiting mechanisms but typically treat the SEI as an idealized interface layer, neglecting spatially resolved transport, solvent consumption, and dynamic interface motion. In this work, we present a continuum-level model for SEI growth grounded in non-equilibrium thermodynamics. The SEI is treated as a distinct thermodynamic domain and modeled as a mixed ion - electron conductor, while the SEI - electrolyte interface is described as a moving boundary. The framework systematically derives transport laws and reaction kinetics from electrochemical poten- tials and interfacial free energies, ensuring thermodynamic consistency. A finite electrolyte reservoir is explicitly included, allowing solvent depletion to emerge naturally as a limiting mechanism for SEI growth. The general formulation consists of coupled partial differential equations for all domains and interfaces. Under open-circuit voltage conditions, the system reduces to a tractable set of ordinary differential equations describing lithium concentration in the active material, solvent concentration, and SEI thickness. Numerical simulations under charging, rest, and cycling conditions reproduce experimentally observed features such as linear and square root of time growth regimes, voltage shifts due to parasitic current consumption, capacity contributions from lithium stored in the SEI, and self- discharge during rest. Two distinct termination mechanisms - active lithium depletion and solvent exhaustion - are identified. Overall, the proposed framework unifies multiple SEI growth mechanisms within a single thermodynamically consistent model and provides a mechanistic basis for improved lifetime prediction and optimization of battery formation and operating protocols. -
I. Papadopoulos, Hierarchical proximal Galerkin: A fast hp--FEM solver for variational problems with pointwise inequality constraints, Preprint no. 3189, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3189 .
Abstract, PDF (47 MByte)
We leverage the proximal Galerkin algorithm (Keith and Surowiec, Foundations of Computational Mathematics, 2024), a recently introduced mesh-independent algorithm, to obtain a high-order finite element solver for variational problems with pointwise inequality constraints. This is achieved by discretizing the saddle point systems, arising from the latent variable proximal point method, with the hierarchical p-finite element basis. This results in discretized sparse Newton systems that admit a simple and effective block preconditioner. The solver can handle both obstacle-type and gradient-type constraints. We apply the resulting algorithm to solve obstacle problems with hp-adaptivity, a gradient-type constrained problem, and the thermoforming problem, an example of an obstacle-type quasi-variational inequality. We observe hp-robustness in the number of Newton iterations and only mild growth in the number of inner Krylov iterations to solve the Newton systems. Crucially we also provide wall-clock timings that are faster than low-order discretization counterparts. -
A. Alphonse, A. Djurdjevac, E. Engström, E. Hansen, Transmission problems and domain decompositions for non--autonomous parabolic equations on evolving domains, Preprint no. 3187, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3187 .
Abstract, PDF (400 kByte)
Parabolic equations on evolving domains model a multitude of applications including various industrial processes such as the molding of heated materials. Such equations are numerically challenging as they require large-scale computations and the usage of parallel hardware. Domain decomposition is a common choice of numerical method for stationary domains, as it gives rise to parallel discretizations. In this study, we introduce a variational framework that extends the use of such methods to evolving domains. In particular, we prove that transmission problems on evolving domains are well posed and equivalent to the corresponding parabolic problems. This in turn implies that the standard non-overlapping domain decompositions, including the Robin-Robin method, become well defined approximations. Furthermore, we prove the convergence of the Robin-Robin method. The framework is based on a generalization of fractional Sobolev-Bochner spaces on evolving domains, time-dependent Steklov-Poincaré operators, and elements of the approximation theory for monotone maps. -
A. Alphonse, G. Wachsmuth, Subdifferentials and penalty approximations of the obstacle problem, Preprint no. 3159, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3159 .
Abstract, PDF (331 kByte)
We consider a framework for approximating the obstacle problem through a penalty approach by nonlinear PDEs. By using tools from capacity theory, we show that derivatives of the solution maps of the penalised problems converge in the weak operator topology to an element of the strong-weak Bouligand subdifferential. We are able to treat smooth penalty terms as well as nonsmooth ones involving for example the positive part function max(0, ·). Our abstract framework applies to several specific choices of penalty functions which are omnipresent in the literature. We conclude with consequences to the theory of optimal control of the obstacle problem. -
A. Alphonse, M. Hintermüller, A. Kister, Ch.H. Lun, C. Sirotenko, A neural network approach to learning solutions of a class of elliptic variational inequalities, Preprint no. 3152, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3152 .
Abstract, PDF (21 MByte)
We develop a weak adversarial approach to solving obstacle problems using neural networks. By employing (generalised) regularised gap functions and their properties we rewrite the obstacle problem (which is an elliptic variational inequality) as a minmax problem, providing a natural formulation amenable to learning. Our approach, in contrast to much of the literature, does not require the elliptic operator to be symmetric. We provide an error analysis for suitable discretisations of the continuous problem, estimating in particular the approximation and statistical errors. Parametrising the solution and test function as neural networks, we apply a modified gradient descent ascent algorithm to treat the problem and conclude the paper with various examples and experiments. Our solution algorithm is in particular able to easily handle obstacle problems that feature biactivity (or lack of strict complementarity), a situation that poses difficulty for traditional numerical methods. -
A. Alphonse, C. Christof, M. Hintermüller, I. Papadopoulos, A globalized inexact semismooth Newton method for nonsmooth fixed-point equations involving variational inequalities, Preprint no. 3132, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3132 .
Abstract, PDF (23 MByte)
We develop a semismooth Newton framework for the numerical solution of fixed-point equations that are posed in Banach spaces. The framework is motivated by applications in the field of obstacle-type quasi-variational inequalities and implicit obstacle problems. It is discussed in a general functional analytic setting and allows for inexact function evaluations and Newton steps. Moreover, if a certain contraction assumption holds, we show that it is possible to globalize the algorithm by means of the Banach fixed-point theorem and to ensure q-superlinear convergence to the problem solution for arbitrary starting values. By means of a localization technique, our Newton method can also be used to determine solutions of fixed-point equations that are only locally contractive and not uniquely solvable. We apply our algorithm to a quasi-variational inequality which arises in thermoforming and which not only involves the obstacle problem as a source of nonsmoothness but also a semilinear PDE containing a nondifferentiable Nemytskii operator. Our analysis is accompanied by numerical experiments that illustrate the mesh-independence and q -superlinear convergence of the developed solution algorithm. -
A. Alphonse, D. Caetano, Ch.M. Elliott, Ch. Venkataraman, Free boundary limits of coupled bulk-surface models for receptor-ligand interactions on evolving domains, Preprint no. 3122, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3122 .
Abstract, PDF (5947 kByte)
We derive various novel free boundary problems as limits of a coupled bulk-surface reaction-diffusion system modelling ligand-receptor dynamics on evolving domains. These limiting free boundary problems may be formulated as Stefan-type problems on an evolving hypersurface. Our results are new even in the setting where there is no domain evolution. The models are of particular relevance to a number of applications in cell biology. The analysis utilises L∞-estimates in the manner of De Giorgi iterations and other technical tools, all in an evolving setting. We also report on numerical simulations. -
M. Dambrine, C. Geiersbach, H. Harbrecht, Two-norm discrepancy and convergence of the stochastic gradient method with application to shape optimization, Preprint no. 3121, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3121 .
Abstract, PDF (447 kByte)
The present article is dedicated to proving convergence of the stochastic gradient method in case of random shape optimization problems. To that end, we consider Bernoulli's exterior free boundary problem with a random interior boundary. We recast this problem into a shape optimization problem by means of the minimization of the expected Dirichlet energy. By restricting ourselves to the class of convex, sufficiently smooth domains of bounded curvature, the shape optimization problem becomes strongly convex with respect to an appropriate norm. Since this norm is weaker than the differentiability norm, we are confronted with the so-called two-norm discrepancy, a well-known phenomenon from optimal control. We therefore need to adapt the convergence theory of the stochastic gradient method to this specific setting correspondingly. The theoretical findings are supported and validated by numerical experiments. -
J. Li, X. Liu, D. Peschka, Local well-posedness and global stability of one-dimensional shallow water equations with surface tension and constant contact angle, Preprint no. 3084, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3084 .
Abstract, PDF (405 kByte)
We consider the one-dimensional shallow water problem with capillary surfaces and moving contact lines. An energy-based model is derived from the two-dimensional water wave equations, where we explicitly discuss the case of a stationary force balance at a moving contact line and highlight necessary changes to consider dynamic contact angles. The moving contact line becomes our free boundary at the level of shallow water equations, and the depth of the shallow water degenerates near the free boundary, which causes singularities for the derivatives and degeneracy for the viscosity. This is similar to the physical vacuum of compressible flows in the literature. The equilibrium, the global stability of the equilibrium, and the local well-posedness theory are established in this paper. -
M.H. Farshbaf Shaker, M. Thomas, Analysis of a compressible Stokes-flow with degenerating and singular viscosity, Preprint no. 2786, WIAS, Berlin, 2020, DOI 10.20347/WIAS.PREPRINT.2786 .
Abstract, PDF (744 kByte)
In this paper we show the existence of a weak solution for a compressible single-phase Stokes flow with mass transport accounting for the degeneracy and the singular behavior of a density-dependent viscosity. The analysis is based on an implicit time-discrete scheme and a Galerkin-approximation in space. Convergence of the discrete solutions is obtained thanks to a diffusive regularization of p-Laplacian type in the transport equation that allows for refined compactness arguments on subdomains. -
A. Münch, B. Wagner, Self-consistent field theory for a polymer brush. Part II: The effective chemical potential, Preprint no. 2649, WIAS, Berlin, 2019, DOI 10.20347/WIAS.PREPRINT.2649 .
Abstract, PDF (318 kByte)
The most successful mean-field model to describe the collective behaviour of the large class of macromolecular polymers is the self-consistent field theory (SCFT). Still, even for the simple system of a grafted dry polymer brush, the mean-field equations have to be solved numerically. As one of very few alternatives that offer some analytical tractability the strong-stretching theory (SST) has led to explicit expressions for the effective chemical potential and consequently the free energy to promote an understanding of the underlying physics. Yet, a direct derivation of these analytical results from the SCFT model is still outstanding. In this study we present a systematic asymptotic theory based on matched asymtptotic expansions to obtain the effective chemical potential from the SCFT model for a dry polymer brush for large but finite stretching. -
A. Münch, B. Wagner, Self-consistent field theory for a polymer brush. Part I: Asymptotic analysis in the strong-stretching limit, Preprint no. 2648, WIAS, Berlin, 2019, DOI 10.20347/WIAS.PREPRINT.2648 .
Abstract, PDF (854 kByte)
In this study we consider the self-consistent field theory for a dry, in- compressible polymer brush, densely grafted on a substrate, describing the average segment density of a polymer in terms of an effective chemical potential for the interaction between the segments of the polymer chain. We present a systematic singular perturbation analysis of the self-consistent field theory in the strong-stretching limit, when the length scale of the ratio of the radius of gyration of the polymer chain to the extension of the brush from the substrate vanishes. Our analysis yields, for the first time, an approximation for the average segment density that is correct to leading order in the outer scaling and resolves the boundary layer singularity at the end of the polymer brush in the strong-stretching limit. We also show that in this limit our analytical results agree increasingly well with our numerical solutions to the full model equations comprising the self-consistent field theory. -
K. Disser, Global existence, uniqueness and stability for nonlinear dissipative systems of bulk-interface interaction, Preprint no. 2313, WIAS, Berlin, 2016, DOI 10.20347/WIAS.PREPRINT.2313 .
Abstract, PDF (302 kByte)
We consider a general class of nonlinear parabolic systems corresponding to thermodynamically consistent gradient structure models of bulk-interface interaction. The setting includes non-smooth geometries and e.g. slow, fast and "entropic” diffusion processes under mass conservation. The main results are global well-posedness and exponential stability of equilibria. As a part of the proof, we show bulk-interface maximum principles and a bulk-interface Poincaré inequality. The method of proof for global existence is a simple but very versatile combination of maximal parabolic regularity of the linearization, a priori L∞-bounds and a Schaefer's fixed point argument. This allows us to extend the setting e.g. to Allen-Cahn dissipative dynamics and to include large classes of inhomogeneous boundary conditions and external forces. -
A. Farina, E. Valdinoci, Anisotropic nonlocal operators regularity and rigidity theorems for a class of anisotropic nonlocal operators, Preprint no. 2213, WIAS, Berlin, 2016, DOI 10.20347/WIAS.PREPRINT.2213 .
Abstract, PDF (284 kByte)
We consider here operators which are sum of (possibly) fractional derivatives, with (possibly different) order. The main constructive assumption is that the operator is of order $2$ in one variable. By constructing an explicit barrier, we prove a Lipschitz estimate which controls the oscillation of the solutions in such direction with respect to the oscillation of the nonlinearity in the same direction. As a consequence, we obtain a rigidity result that, roughly speaking, states that if the nonlinearity is independent of a coordinate direction, then so is any global solution (provided that the solution does not grow too much at infinity). A Liouville type result then follows as a byproduct. -
V. Barbu, P. Colli, G. Gilardi, G. Marinoschi, E. Rocca, Sliding modes for a phase-field system, Preprint no. 2133, WIAS, Berlin, 2015, DOI 10.20347/WIAS.PREPRINT.2133 .
Abstract, PDF (295 kByte)
In the present contribution the sliding mode control (SMC) problem for a phase-field model of Caginalp type is considered. First we prove the well-posedness and some regularity results for the phase-field type state systems modified by the state- feedback control laws. Then, we show that the chosen SMC laws force the system to reach within finite time the sliding manifold (that we chose in order that one of the physical variables or a combination of them remains constant in time). We study three different types of feedback control laws: the first one appears in the internal energy balance and forces a linear combination of the temperature and the phase to reach a given (space dependent) value, while the second and third ones are added in the phase relation and lead the phase onto a prescribed target $phi^*$. While the control law is non-local in space for the first two problems, it is local in the third one, i.e., its value at any point and any time just depends on the value of the state. -
W. Dreyer, J. Giesselmann, Ch. Kraus, Modeling of compressible electrolytes with phase transition, Preprint no. 1955, WIAS, Berlin, 2014, DOI 10.20347/WIAS.PREPRINT.1955 .
Abstract, PDF (457 kByte)
A novel thermodynamically consistent diffuse interface model is derived for compressible electrolytes with phase transitions. The fluid mixtures may consist of N constituents with the phases liquid and vapor, where both phases may coexist. In addition, all constituents may consist of polarizable and magnetizable matter. Our introduced thermodynamically consistent diffuse interface model may be regarded as a generalized model of Allen-Cahn/Navier-Stokes/Poisson type for multi-component flows with phase transitions and electrochemical reactions. For the introduced diffuse interface model, we investigate physically admissible sharp interface limits by matched asymptotic techniques. We consider two scaling regimes, i.e. a non-coupled and a coupled regime, where the coupling takes place between the smallness parameter in the Poisson equation and the width of the interface. We recover in the sharp interface limit a generalized Allen-Cahn/Euler/Poisson system for mixtures with electrochemical reactions in the bulk phases equipped with admissible interfacial conditions. The interfacial conditions satisfy, for instance, a generalized Gibbs-Thomson law and a dynamic Young-Laplace law. -
P.-É. Druet, A curvature estimate for open surfaces subject to a general mean curvature operator and natural contact conditions at their boundary, Preprint no. 1897, WIAS, Berlin, 2013, DOI 10.20347/WIAS.PREPRINT.1897 .
Abstract, PDF (251 kByte)
In the seventies, L. Simon showed that the main curvatures of two-dimensional hypersurfaces obeying a general equation of mean curvature type are a priori bounded by the Hölder norm of the coefficients of the surface differential operator. This was an essentially interior estimate. In this paper, we provide a complement to the theory, proving a global curvature estimate for open surfaces that satisfy natural contact conditions at the intersection with a given boundary.
 Talks, Poster
Talks, Poster
-
I. Papadopoulos, Hierarchical proximal Galerkin: A fast hp--FEM solver for variational problems with pointwise inequality constraints, Scientific Computing Seminars, Brown University, Division of Applied Mathematics, Providence, Rhode Island, USA, April 11, 2025.
-
I. Papadopoulos, The latent variable proximal point algorithm for variational problems with inequality constraints, 30th Biennial Conference on Numerical Analysis, Minisymposium M22 ``Advancements and applications of solvers for PDE systems with nonsmooth structures", June 24 - 27, 2025, University of Strathclyde, Glasgow, UK, June 26, 2025.
-
A. Alphonse, A neural network approach to learning solutions of a class of elliptic variational inequalities, European Conference on Numerical Mathematics and Advanced Applications (ENUMATH 2025), Minisymposium MS 25-1 ``Numerical Methods for Moving Interface and Free Boundary Problems'', September 1 - 5, 2025, Universität Heidelberg, September 3, 2025.
-
M. Hintermüller, A neural network approach to learning solutions of a class of elliptic variational inequalities, ALOP International Workshop on Algorithmic Optimization 2025, September 23 - 26, 2025, Universität Trier, September 24, 2025.
-
M. Hintermüller, A neural network approach to learning solutions of a class of elliptic variational inequalities, The Mathematics of Scientific Machine Learning and Digital Twins, November 20 - 24, 2025, International School of Mathematics "G. Stampacchia", Erice, Italy, November 21, 2025.
-
I. Papadopoulos, A semismooth Newton method for obstacle-type quasivariational inequalities, Firedrake 2024 (8th Firedrake user and developer workshop), September 16 - 18, 2024, University of Oxford, UK, September 18, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 23rd Symposium on Trends in Applications of Mathematics to Mechanics (STAMM 2024), April 3 - 5, 2024, Julius-Maximilians-Universität Würzburg, April 5, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, 9th European Congress of Mathematics (9ECM), Minisymposium 27 ``New Trends in Calculus of Variations'', July 15 - 19, 2024, Universidad de Sevilla, Spain, July 16, 2024.
-
M. Thomas, Analysis of a model for visco-elastoplastic two-phase flows in geodynamics, Seminar on Nonlinear Partial Differential Equations, Texas A&M University, Department of Mathematics, College Station, USA, March 19, 2024.
-
A. Alphonse, Risk--averse optimal control of elliptic variational inequalities, 94th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2024), Session 19.01 ``Various Topics in Optimization of Differential Equations'', March 18 - 22, 2024, Otto-von-Guericke-Universität Magdeburg, March 19, 2024.
-
M. Hintermüller, A neural network approach to learning solutions of a class of elliptic variational inequalities, Nonsmooth Optimization and Variational Analysis, December 2 - 4, 2024, The Hong Kong Polytechnic University, China, December 4, 2024.
-
M. Hintermüller, A neural network approach to learning solutions of a class of elliptic variational inequalities, Chinese University of Hong Kong, Department of Mathematics, China, December 12, 2024.
-
M. Hintermüller, A neural network approach to learning solutions of a class of elliptic variational inequalities, colloquium talk, Hunan Normal University, Department of Mathematics, Changsha, China, December 10, 2024.
-
M. Hintermüller, PINNs in multiscale materials as PDE-constrained optimization problem, Forum for Mathematical Optimization with PDEs, Central South University, Changsha, China, December 9, 2024.
-
M. Hintermüller, QVIs: Semismooth Newton, optimal control and uncertainties, colloquium talk, Hunan Normal University, Department of Mathematics, Changsha, China, December 10, 2024.
-
M. Hintermüller, QVIs: Semismooth Newton, optimal control, and uncertainties, RICAM Colloquium, Johann Radon Institute for Computational and Applied Mathematics (RICAM), Linz, Austria, June 27, 2024.
-
M. Hintermüller, Risk-averse optimal control of random elliptic VIs, SIAM Conference on Uncertainty Quantification (UQ24), Minisymposium MS43 ``Efficient Solution Schemes for Optimization of Complex Systems Under Uncertainty'', February 27 - March 1, 2024, Savoia Excelsior Palace Trieste and Stazione Marittima, Italy, February 27, 2024.
-
D. Peschka, Moving contact lines for sliding droplets, 93rd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2023), Session 11 ``Interfacial Flows'', May 30 - June 2, 2023, Technische Universität Dresden, June 1, 2023.
-
D. Peschka, Multiscale limits of thin-film models with moving support, In Search of Model Structures for Non-equilibrium Systems, April 24 - 28, 2023, Westfälische Wilhelms-Universität Münster, April 27, 2023.
-
D. Peschka, Sharp-interface limit of models with mechanics and contact lines, 10th International Congress on Industrial and Applied Mathematics (ICIAM 2023), Session 00247 ``Interfaces and Free Boundaries in Fluid Mechanics and Materials Science'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 24, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Annual Workshop of the GAMM Activity Group on Analysis of PDEs, September 18 - 20, 2023, Katholische Universität Eichstätt-Ingolstadt, September 20, 2023.
-
M. Thomas, Damage in viscoelastic materials at finite strains, Workshop ``Variational Methods for Evolution'', December 3 - 8, 2023, Mathematisches Forschungsinstitut Oberwolfach, December 7, 2023.
-
M. Thomas, Some aspects of damage in nonlinearly elastic materials: From damage to delamination in nonlinearly elastic materials, Variational and Geometric Structures for Evolution, October 9 - 13, 2023, Università Commerciale Luigi Bocconi, Levico Terme, Italy, October 10, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Nonlinear PDEs: Recent Trends in the Analysis of Continuum Mechanics, July 17 - 21, 2023, Universität Bonn, Hausdorff School for Advanced Studies in Mathematics, July 17, 2023.
-
M. Thomas, Approximating dynamic phase-field fracture with a first-order formulation for velocity and stress, Seminar für Angewandte Mathematik, Technische Universität Dresden, June 5, 2023.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, March 27, 2023.
-
A. Alphonse, Analysis of a quasi-variational contact problem arising in thermoelasticity, European Conference on Computational Optimization (EUCCO), Session ``Non-smooth Optimization'', September 25 - 27, 2023, Universität Heidelberg, September 25, 2023.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets (online talk), Workshop ``Control Methods in Hyperbolic Partial Differential Equations'' (Hybrid Event), November 5 - 10, 2023, Mathematisches Forschungsinstitut Oberwolfach, November 7, 2023.
-
D. Peschka, Variational approach for wetting flows on solid and soft substrates (online talk), Colloquium of the SPP 2171 (Online Event), Westfälische Wilhelms-Universität Münster, January 28, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, PHAse field MEthods in applied sciences (PHAME 2022), May 23 - 27, 2022, Istituto Nazionale di Alta Matematica, Rome, Italy, May 25, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, Beyond Elasticity: Advances and Research Challenges, May 16 - 20, 2022, Centre International de Rencontres Mathématiques, Marseille, France, May 16, 2022.
-
M. Thomas, First-order formulation for dynamic phase-field fracture in visco-elastic materials, Jahrestreffen des SPP 2256, September 28 - 30, 2022, Universität Regensburg, September 30, 2022.
-
A. Alphonse, Directional differentiability and optimal control for elliptic quasi-variational inequalities (online talk), Workshop ``Challenges in Optimization with Complex PDE-Systems'' (Hybrid Workshop), February 14 - 20, 2021, Mathematisches Forschungsinstitut Oberwolfach, February 17, 2021.
-
A. Alphonse, Directional differentiability and optimal control for elliptic quasi-variational inequalities (online talk), Meeting of the Scientific Advisory Board of WIAS, WIAS Berlin, March 12, 2021.
-
A. Alphonse, Some aspects of sensitivity analysis and optimal control for elliptic QVIs (coauthors: Michael Hintermüller and Carlos Rautenberg, online talk), 91th Annual Meeting of the International Association of Applied Mathematics and Mechanics (Online Event), Session DFG-PP 1962 Non-smooth and Complementarity-based Distributed Parameter Systems, March 15 - 19, 2021, Universität Kassel, March 16, 2021.
-
A. Alphonse, Some aspects of sensitivity analysis and optimal control for elliptic QVIs (online talk), Annual Meeting of the DFG SPP 1962 (Virtual Conference), March 24 - 25, 2021, WIAS Berlin, March 25, 2021.
-
X. Liu, Second law of thermodynamics and bounded entropy solutions in the compressible Navier--Stokes system, Summer School 2021 ``Wave Phenomena: Analysis and Numerics'' (Hybrid Event), September 27 - 30, 2021.
-
D. Peschka, Dynamic contact angles and their numerical discretization for gradient systems (online talk), 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (Online Event), September 13 - 17, 2021, WIAS Berlin, September 13, 2021.
-
D. Peschka, Mathematical modeling and simulation of substrate-flow interaction using generalized gradient flows, Conference ``Dynamic Wetting of Flexible, Adaptive, and Switchable Substrates'' of the SPP 2171, Freiburg, November 8 - 10, 2021.
-
D. Peschka, Mathematical modeling and simulation of substrate-flow interaction using generalized gradient flows, SPP 2171 Conference ``Dynamic Wetting of Flexible, Adaptive, and Switchable Substrates'', November 8 - 10, 2021, Albert-Ludwigs-Universität Freiburg, November 10, 2021.
-
D. Peschka, Self-similar spreading with dynamic contact angles (online talk), 91st Annual Meeting of the International Association of Applied Mathematics and Mechanics (Online Event), Section S11 ``Interfacial Flows'', March 15 - 19, 2021, Universität Kassel, March 17, 2021.
-
D. Peschka, Thin-film problems with dynamic contact angle (online talk), 8th European Congress of Mathematics (8ECM), Minisymposium ID 43 ``Higher-order Evolution Equations'' (Online Event), June 20 - 26, 2021, Portoroč, Slovenia, June 23, 2021.
-
C. Geiersbach, Stochastic approximation for optimization in shape spaces, 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (FBP 2021, Online Event), Minisymposium ``UQ in Free Boundary Problems'', September 13 - 17, 2021, WIAS, Berlin, September 14, 2021.
-
M. Thomas, Convergence analysis for fully discretized damage and phase-field fracture models (online talk), 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (FBP 2021, Online Event), Minisymposium ``Phase Field Models'', September 13 - 17, 2021, WIAS, Berlin, September 14, 2021.
-
M. Hintermüller, Optimal control of quasi-variational inequalities (online talk), SIAM Conference on Optimization (OP21) (Online Event), Minisymposium MS93 ``Nonsmooth Problems and Methods in Large-scale Optimization'', July 20 - 23, 2021, July 23, 2021.
-
X. Liu, Second law of thermodynamics and bounded entropy solutions in the compressible Navier--Stokes system (online talk), 15th International Conference on Free Boundary Problems: Theory and Applications 2021 (Online Event), September 13 - 17, 2021, WIAS Berlin, September 17, 2021.
-
D. Peschka, Mathematical modeling and simulation of flows and the interaction with a substrate using energetic variational methods, CRC 1194 ``Interaction between Transport and Wetting Processes'', Technische Universität Darmstadt, January 22, 2020.
-
D. Peschka, Variational modeling of bulk and interface effects in fluid dynamics, SPP 2171 Advanced School ``Introduction to Wetting Dynamics'', February 17 - 21, 2020, Westfälische Wilhelms-Universität Münster, February 18, 2020.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, MATH+ Day 2020 (Online Event), Berlin, November 6, 2020.
-
M. Thomas, Modeling and analysis of flows of concentrated suspensions (online talk), Colloquium of the RTG 2339 ``Interfaces, Complex Structures, and Singular Limits'' (Online Event), Universität Regensburg, July 10, 2020.
-
M. Thomas, Nonlinear fracture dynamics: Modeling, analysis, approximation, and applications, Presentation of project proposals in SPP 2256 ``Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials'', Bad Honnef, January 30, 2020.
-
M. Thomas, Thermodynamical modelling via energy and entropy functionals (online talks), Thematic Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Student Compact Course ``Variational Methods for Fluids and Solids'' (Online Event), October 12 - 23, 2020, WIAS Berlin.
-
M. Thomas, Weierstraß-Gruppe "Volumen-Grenzschicht-Prozesse", Sitzung des Wissenschaftlichen Beirats, WIAS Berlin, September 18, 2020.
-
B. Wagner, Pattern formation in dewetting films (online talk), Workshop ``Mathematical Modeling and Scientific Computing: Focus on Complex Processes and Systems'' (Online Event), November 19 - 20, 2020, Technische Universität München, November 19, 2020.
-
B. Wagner, Phase-field models of the lithiation/delithiation cycle of thin-film electrodes (online talk), Oxford Battery Modelling Symposium (Online Event), March 16 - 17, 2020, University of Oxford, UK, March 16, 2020.
-
J.A. Brüggemann, Elliptic obstacle-type quasi-variational inequalities (QVIs) with volume constraints motivated by a contact problem in biomedicine, ICCOPT 2019 -- Sixth International Conference on Continuous Optimization, Berlin, August 5 - 8, 2019.
-
J.A. Brüggemann, Solution methods for a class of obstacle-type quasi variational inequalities with volume constraints, ICCOPT 2019 -- Sixth International Conference on Continuous Optimization, Session ``Quasi-Variational Inequalities and Generalized Nash Equi-librium Problems (Part II)'', August 5 - 8, 2019, Berlin, August 7, 2019.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, Visit of the Scientific Advisory Board of MATH+, November 11, 2019.
-
M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of suspension flows, 1st MATH+ Day, Berlin, December 13, 2019.
-
D. Peschka, Dynamic contact angles via generalized gradient flows, Modelling of Thin Liquid Films -- Asymptotic Approach vs. Gradient Dynamics, April 28 - May 3, 2019, Banff International Research Station for Mathematical Information and Discovery, Canada, April 30, 2019.
-
D. Peschka, Dynamic contact angles via gradient flows, 694. WE-Heraeus-Seminar ``Wetting on Soft or Microstructured Surfaces'', Bad Honnef, April 10 - 13, 2019.
-
D. Peschka, Gradient formulations with flow maps -- Mathematical and numerical approaches to free boundary problems, Kolloquium des Graduiertenkollegs 2339 ``Interfaces, Complex Structures, and Singular Limits'', Universität Regensburg, May 24, 2019.
-
D. Peschka, Mathematical modeling and simulation of substrate-flow interaction using generalized gradient flow, Begutachtungskolloquium für die Anträge des SPP 2171 ``Dynamische Benetzung flexibler, adaptiver und schaltbarer Oberflächen'', Mainz, February 7 - 8, 2019.
-
D. Peschka, Mathematical modeling of fluid flows using gradient systems, Seminar in PDE and Applications, Delft University of Technology, Netherlands, May 28, 2019.
-
D. Peschka, Steering pattern formation of viscous flows, DMV-Jahrestagung 2019, Sektion ``Differentialgleichungen und Anwendungen'', September 23 - 26, 2019, KIT - Karlsruher Institut für Technologie, September 23, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems, MURPHYS-HSFS 2019 Summer School on Multi-Rate Processes, Slow-Fast Systems and Hysteresis, June 17 - 19, 2019, Politecnico di Torino, Turin, Italy.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Mathematics for Mechanics, October 29 - November 1, 2019, Czech Academy of Sciences, Prague, Czech Republic, October 31, 2019.
-
M. Thomas, Coupling of rate-independent and rate-dependent systems with application to delamination processes in solids, Seminar ``Applied and Computational Analysis'', University of Cambridge, UK, October 10, 2019.
-
M. Thomas, GENERIC structures with bulk-interface interaction, SFB 910 Symposium ``Energy Based Modeling, Simulation and Control'', October 25, 2019, Technische Universität Berlin, October 25, 2019.
-
M. Thomas, Gradient structures for flows of concentrated suspensions, 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019), Thematic Minisymposium MS ME-7-75 ``Recent Advances in Understanding Suspensions and Granular Media Flow'', July 15 - 19, 2019, Valencia, Spain, July 17, 2019.
-
M. Thomas, Rate-independent evolution of sets and application to fracture processes, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S14 ``Applied Analysis'', February 18 - 22, 2019, Technische Universität Wien, Austria, February 20, 2019.
-
B. Wagner, Free boundary problems of active and driven hydrogels, PIMS-Germany Workshop on Modelling, Analysis and Numerical Analysis of PDEs for Applications, June 24 - 26, 2019, Universität Heidelberg, Interdisciplinary Center for Scientific Computing and BIOQUANT Center, June 24, 2019.
-
B. Wagner, Free boundary problems of active and driven hydrogels, EUROMECH 604, Fluid and Solid Mechanics for Issue Engineering, September 23 - 25, 2019, University of Oxford, Mathematical Institute, UK, September 24, 2019.
-
M. Hintermüller, Lecture Series: Optimal control of nonsmooth structures, Thematic Programme ``Modern Maximal Monotone Operator Theory: From Nonsmooth Optimization to Differential Inclusions'', February 4 - 7, 2019, Erwin Schrödinger International Institute for Mathematics and Physics, Vienna, Austria.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, Colloquium of the Mathematical Institute, University of Oxford, UK, June 7, 2019.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, Polish Academy of Sciences, Systems Research Institute, Warsaw, Poland, December 3, 2019.
-
J.A. Brüggemann, Path-following methods for a class of elliptic obstacle-type quasi-variational problems with integral constraints, 23rd International Symposium on Mathematical Programming (ISMP2018), Session 370 ``Variational Analysis 4'', July 1 - 6, 2018, Bordeaux, France, July 2, 2018.
-
M. Thomas, D. Peschka, B. Wagner, V. Mehrmann, M. Rosenau, Modeling and analysis of suspension flows, MATH+ Center Days 2018, October 31 - November 2, 2018, Zuse-Institut Berlin (ZIB), Berlin, October 31, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), Section DFG Priority Programmes PP1748 ``Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretization Methods, Mechanical and Mathematical Analysis'', March 19 - 23, 2018, Technische Universität München, March 20, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, Workshop ``Special Materials and Complex Systems'' (SMACS 2018), June 18 - 22, 2018, University of Milan/University of Pavia, Gargnano, Italy, June 18, 2018.
-
M. Thomas, Analysis and simulation for a phase-field fracture model at finite strains based on modified invariants, Analysis Seminar, University of Brescia, Department of Mathematics, Italy, May 10, 2018.
-
M. Thomas, Gradient structures for flows of concentrated suspensions, The 12th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 18 ``Emergence and Dynamics of Patterns in Nonlinear Partial Differential Equations and Related Fields'', July 5 - 9, 2018, National Taiwan University, Taipeh, Taiwan, Province Of China, July 7, 2018.
-
M. Hintermüller, Nonsmooth structures in PDE constrained optimization, Mathematisches Kolloquium, Universität Bielefeld, Fakultät für Mathematik, June 7, 2018.
-
C.N. Rautenberg, Dissipative and non-dissipative evolutionary quasi-variational inequalities with derivative constraints, Joint Meeting of the Italian Mathematical Union, the Italian Society of Industrial and Applied Mathematics and the Polish Mathematical Society, Session 14 ``Nonlinear Variational Methods with Applications'', September 17 - 20, 2018, Wroclaw, Poland, September 19, 2018.
-
A. Alphonse, Optimal control of elliptic and parabolic quasi-variational inequalities, Annual Meeting of the DFG Priority Programme 1962, October 9 - 11, 2017, Kremmen (Sommerfeld), October 10, 2017.
-
D. Peschka, Mathematical and numerical approaches to moving contact lines, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, December 6, 2017.
-
D. Peschka, Motion of thin droplets over surfaces, Making a Splash -- Driplets, Jets and Other Singularities, March 20 - 24, 2017, Brown University, Institute for Computational and Experimental Research in Mathematics (ICERM), Providence, USA, March 22, 2017.
-
D. Peschka, Variational structure of fluid motion with contact lines in thin-film models, Kolloquium Angewandte Mathematik, Universität der Bundeswehr, München, May 31, 2017.
-
M. Hintermüller, Adaptive finite element solvers for MPECs in function space, SIAM Conference on Optimization, Minisymposium MS122 ``Recent Trends in PDE-Constrained Optimization'', May 22 - 25, 2017, Vancouver, British Columbia, Canada, May 25, 2017.
-
M. Hintermüller, Generalized Nash games with partial differential equations, Kolloquium Arbeitsgruppe Modellierung, Numerik, Differentialgleichungen, Technische Universität Berlin, June 20, 2017.
-
M. Hintermüller, Non-smooth structures in PDE-constrained optimization, Mathematisches Kolloquium, Universität Duisburg-Essen, Fakultät für Mathematik, Essen, January 11, 2017.
-
M. Hintermüller, Nonsmooth structures in PDE constrained optimization, Optimization Seminar, Chinese Academy of Sciences, State Key Laboratory of Scientific and Engineering Computing, Beijing, China, June 6, 2017.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, Kolloquium, Friedrich-Alexander-Universität Erlangen-Nürnberg, Department Mathematik, Erlangen, May 2, 2017.
-
M. Hintermüller, Optimal control of multiphase fluids based on non smooth models, 14th International Conference on Free Boundary Problems: Theory and Applications, Theme Session 8 ``Optimization and Control of Interfaces'', July 9 - 14, 2017, Shanghai Jiao Tong University, China, July 10, 2017.
-
M. Hintermüller, Recent trends in PDE-constrained optimization with non-smooth structures, Fourth Conference on Numerical Analysis and Optimization (NAOIV-2017), January 2 - 5, 2017, Sultan Qaboos University, Muscat, Oman, January 4, 2017.
-
D. Peschka, A free boundary problem for the flow of viscous liquid bilayers, ERC Workshop on Modeling Materials and Fluids using Variational Methods, February 22 - 26, 2016, WIAS Berlin, Berlin, February 26, 2016.
-
D. Peschka, A free boundary problem for the motion of viscous liquids, 7th European Congress of Mathematics (7ECM), Minisymposium 29 ``Nonsmooth PDEs in the Modeling Damage, Delamination, and Fracture'', July 18 - 22, 2016, Technische Universität Berlin, July 22, 2016.
-
D. Peschka, Multi-phase flows with contact lines: Solid vs liquid substrates, Industrial and Applied Mathematics Seminar, University of Oxford, Mathematical Institute, UK, October 27, 2016.
-
D. Peschka, Thin film free boundary problems --- Modeling of contact line dynamics with gradient formulations, CeNoS-Kolloquium, Westfälische Wilhelms-Universität Münster, Center for Nonlinear Science, January 12, 2016.
-
E. Valdinoci, A notion of fractional perimeter and nonlocal minimal surfaces, Seminar, Universitá del Salento, Dipartimento di Matematics e Fisica ``Ennio de Giorgi'', Lecce, Italy, June 22, 2016.
-
E. Valdinoci, Interior and boundary properties of nonlocal minimal surfaces, Calcul des Variations & EDP, Université Aix-Marseille, Institut de Mathématiques de Marseille, France, February 25, 2016.
-
E. Valdinoci, Interior and boundary properties on nonlocal minimal surfaces, 3rd Conference on Nonlocal Operators and Partial Differential Equations, June 27 - July 1, 2016, Bedlewo, Poland, June 27, 2016.
-
E. Valdinoci, Nonlocal Equations and Applications, Spring School on Nonlinear PDEs and Related Problems, January 15 - 19, 2016, African Institute for Mathematical Sciences (AIMS), Mbour, Senegal.
-
E. Valdinoci, Nonlocal equations and applications, Calculus of Variations and Nonlinear Partial Differential Equations, May 16 - 27, 2016, Columbia University, Department of Mathematics, New York, USA, May 25, 2016.
-
E. Valdinoci, Nonlocal equations from various perspectives, PIMS Workshop on Nonlocal Variational Problems and PDEs, June 13 - 17, 2016, University of British Columbia, Vancouver, Canada, June 13, 2016.
-
E. Valdinoci, Nonlocal minimal surface, Justus-Liebig-Universität Gießen, Fakultät für Mathematik, February 10, 2016.
-
E. Valdinoci, Nonlocal minimal surfaces, Analysis, PDEs, and Geometry Seminar, Monash University, Clayton, Australia, August 9, 2016.
-
E. Valdinoci, Nonlocal minimal surfaces, a geometric and analytic insight, Seminar on Differential Geometry and Analysis, Otto-von-Guericke-Universität Magdeburg, January 18, 2016.
-
E. Valdinoci, Nonlocal minimal surfaces: Regularity and quantitative properties, Conference on Recent Trends on Elliptic Nonlocal Equations, The Fields Institute for Research in Mathematical Sciences, Toronto, Canada, June 9, 2016.
-
M.H. Farshbaf Shaker, A phase field approach for optimal boundary control of damage processes in two-dimensional viscoelastic media, International INdAM Conference ``Optimal Control for Evolutionary PDEs and Related Topics (OCERTO 2016)'', June 20 - 24, 2016, Cortona, Italy, June 21, 2016.
-
S.P. Frigeri, On a diffuse interface model of tumor growth, 9th European Conference on Elliptic and Parabolic Problems, May 23 - 27, 2016, University of Zurich, Institute of Mathematics, Gaeta, Italy, May 23, 2016.
-
M. Hintermüller, Nonsmooth structures in PDE constrained optimization, 66th Workshop ``Advances in Convex Analysis and Optimization'', July 5 - 10, 2016, International Centre for Scientific Culture ``E. Majorana'', School of Mathematics ``G. Stampacchia'', Erice, Italy, July 9, 2016.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, WIAS-PGMO Workshop on Nonsmooth and Stochastic Optimization with Applications to Energy Management, May 10 - 12, 2016, WIAS Berlin, May 11, 2016.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, The Fifth International Conference on Continuous Optimization, Session: ``Recent Developments in PDE-constrained Optimization I'', August 6 - 11, 2016, Tokyo, Japan, August 10, 2016.
-
M. Hintermüller, Optimal control of multiphase fluids and droplets, Salzburg Mathematics Colloquium, Universität Salzburg, Fachbereich Mathematik, Austria, June 9, 2016.
-
M. Hintermüller, Recent trends in optimal control problems with nonsmooth structures, Computational Methods for Control of Infinite-dimensional Systems, March 14 - 18, 2016, Institute for Mathematics and its Applications, Minneapolis, USA, March 14, 2016.
-
M. Hintermüller, Towards sharp stationarity conditions for classes of optimal control problems for variational inequalities of the second kind, International INdAM Conference ``Optimal Control for Evolutionary PDEs and Related Topics (OCERTO 2016)'', June 20 - 24, 2016, Cortona, Italy, June 20, 2016.
-
E. Valdinoci, Nonlocal equations in phase transitions, minimal surfaces, crystallography and life sciences, Escuela CAPDE Ecuaciones diferenciales parciales no lineales, Universidad de Chile, Facultad de Ciencias Físicas y Matemáticas, Santiago de Chile, Chile.
-
E. Cinti, A quantitative weighted isoperimetric inequality via the ABP method, Oberseminar Analysis, Universität Bonn, Institut für Angewandte Mathematik, February 5, 2015.
-
E. Cinti, Quantitative isoperimetric inequality via the ABP method, Università di Bologna, Dipartimento di Matematica, Bologna, Italy, July 17, 2015.
-
S. Patrizi, Dislocations dynamics: From microscopic models to macroscopic crystal plasticity, Analysis Seminar, The University of Texas at Austin, Department of Mathematics, USA, January 21, 2015.
-
S. Patrizi, Dislocations dynamics: From microscopic models to macroscopic crystal plasticity, Seminar, King Abdullah University of Science and Technologie, SRI -- Center for Uncertainty Quantification in Computational Science & Engineering, Jeddah, Saudi Arabia, March 25, 2015.
-
S. Patrizi, On a long range segregation model, Seminar, Università degli Studi di Salerno, Dipartimento di Matematica, Italy, May 19, 2015.
-
S. Patrizi, On a long range segregation model, Seminario di Analisi Matematica, Sapienza Università di Roma, Dipartimento di Matematica ``Guido Castelnuovo'', Italy, April 20, 2015.
-
E. Rocca, Optimal control of a nonlocal convective Cahn--Hilliard equation by the velocity, Numerical Analysis Seminars, Durham University, UK, March 13, 2015.
-
S.P. Frigeri, On a diffuse interface model of tumor growth, INdAM Workshop ``Special Materials in Complex Systems -- SMaCS 2015'', May 18 - 22, 2015, Rome, Italy, May 22, 2015.
-
S.P. Frigeri, On a nonlocal diffuse interface model for binary incompressible fluids with different densities, Mathematical Thermodynamics of Complex Fluids, June 28 - July 3, 2015, Fondazione CIME ``Roberto Conti'' (International Mathematical Summer Center), Cetraro, Italy, July 2, 2015.
-
S.P. Frigeri, Recent results on optimal control for Cahn--Hilliard/Navier--Stokes systems with nonlocal interactions, Control Theory and Related Topics, April 13 - 14, 2015, Politecnico di Milano, Italy, April 13, 2015.
-
M. Heida, Modeling of fluid interfaces, Jahrestagung der Deutschen Mathematiker-Vereinigung, Minisymposium ``Mathematics of Fluid Interfaces'', September 21 - 25, 2015, Universität Hamburg, Fakultät für Mathematik, Informatik und Naturwissenschaften, Hamburg, September 23, 2015.
-
D. Peschka, Droplets on liquids and their long way into equilibrium, Minisymposium ``Recent Progress in Modeling and Simulation of Multiphase Thin-film Type Problems'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 10 - 14, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 12, 2015.
-
D. Peschka, Modeling and applications of bilayer flows, Seminar of the Research Training Group GRK 1276 ``Structure Formation and Transport in Complex Systems'', Universität des Saarlandes, Institut für Theoretische Physik, Saarbrücken, January 27, 2015.
-
D. Peschka, Numerics of contact line motion for thin films, MATHMOD 2015, Minisymposium ``Free Boundary Problems in Applications: Recent Advances in Modelling, Simulation and Optimization'', February 17 - 20, 2015, Technische Universität Wien, Institut für Analysis und Scientific Computing, Wien, Austria, February 19, 2015.
-
D. Peschka, Thin-film equations with free boundaries, Jahrestagung der Deutschen Mathematiker-Vereinigung, Minisymposium ``Mathematics of Fluid Interfaces'', September 21 - 25, 2015, Universität Hamburg, Fakultät für Mathematik, Informatik und Naturwissenschaften, Hamburg, September 23, 2015.
-
E. Valdinoci, Dislocation dynamics in crystals: Nonlocal effects, collisions and relaxation, Mostly Maximum Principle, September 16 - 18, 2015, Castello Aragonese, Agropoli, Italy, September 16, 2015.
-
E. Valdinoci, Dislocation dynamics in crystals: Nonlocal effects, collisions and relaxation, Second Workshop on Trends in Nonlinear Analysis, September 24 - 26, 2015, GNAMPA, Universitá degli Studi die Cagliari, Dipartimento di Matematica e Informatica, Cagliari, Italy, September 26, 2015.
-
E. Valdinoci, Minimal surfaces and phase transitions with nonlocal interactions, Analysis Seminar, University of Edinburgh, School of Mathematics, UK, March 23, 2015.
-
E. Valdinoci, Nonlocal Problems in Analysis and Geometry, 2° Corso Intensivo di Calcolo delle Variazioni, June 15 - 20, 2015, Dipartimento di Matematica e Informatica di Catania, Italy.
-
E. Valdinoci, Nonlocal minimal surfaces, Seminario di Calcolo delle Variazioni & Equazioni alle Derivate Parziali, Università degli Studi di Firenze, Dipartimento di Matematica e Informatica ``Ulisse Dini'', Italy, March 13, 2015.
-
E. Valdinoci, Nonlocal problems -- Theory and applications, School/Workshop ``Phase Transition Problems and Nonlinear PDEs'', March 9 - 11, 2015, Università di Bologna, Dipartimento di Matematica.
-
E. Valdinoci, Nonlocal problems and applications, Summer School on ``Geometric Methods for PDEs and Dynamical Systems'', June 8 - 11, 2015, École Normale Supérieure de Lyon, Unité de Mathématiques Pures et Appliquées and Institut de Mathématiques, Equipe d'Analyse, Université Bordeaux 1, Porquerolles, France.
-
E. Valdinoci, Some models arising in crystal dislocations, Global Dynamics in Hamiltonian Systems, June 28 - July 4, 2015, Universitat Politècnica de Catalunya (BarcelonaTech), Girona, Spain, June 29, 2015.
-
E. Valdinoci, What is the (fractional) Laplacian?, Perlen-Kolloquium, Universität Basel, Fachbereich Mathematik, Switzerland, May 22, 2015.
-
E. Rocca, ``Entropic'' solutions to a thermodynamically consistent PDE system for phase transitions and damage, Symposium on Trends in Application of Mathematics to Mechanics (STAMM), September 8 - 11, 2014, International Society for the Interaction of Mechanics and Mathematics (ISIMM), Poitiers, France, September 9, 2014.
-
E. Valdinoci, (Non)local interfaces and minimal surfaces, International Conference on ``Nonlinear Phenomena in Biology'', March 5 - 7, 2014, Helmholtz Zentrum München -- Deutsches Forschungszentrum für Gesundheit und Umwelt, March 5, 2014.
-
E. Valdinoci, Concentrating solutions for a nonlocal Schroedinger equation, Nonlinear Partial Differential Equations and Stochastic Methods, June 7 - 11, 2014, University of Jyväskylä, Finland, June 10, 2014.
-
E. Valdinoci, Concentration phenomena for nonlocal equation, Méthodes Géométriques et Variationnelles pour des EDPs Non-linéaires, September 1 - 5, 2014, Université C. Bernard, Lyon 1, Institut C. Jordan, France, September 2, 2014.
-
E. Valdinoci, Concentration solutions for a nonlocal Schroedinger equation, Kinetics, Non Standard Diffusion and the Mathematics of Networks: Emerging Challenges in the Sciences, May 7 - 16, 2014, The University of Texas at Austin, Department of Mathematics, USA, May 14, 2014.
-
E. Valdinoci, Dislocation dynamics and fractional equations, Analysis Seminar, Heriot-Watt University of Edinburgh, London, UK, October 31, 2014.
-
E. Valdinoci, Dislocation dynamics and fractional equations, Analysis Seminar, University of Texas at Austin Mathematics, USA, November 5, 2014.
-
E. Valdinoci, Dislocation dynamics in crystals, Recent Advances in Non-local and Non-linear Analysis: Theory and Applications, June 10 - 14, 2014, FIM -- Institute for Mathematical Research, ETH Zuerich, Switzerland, June 13, 2014.
-
E. Valdinoci, Dislocation dynamics in crystals, Geometry and Analysis Seminar, Columbia University, Department of Mathematics, New York City, USA, April 3, 2014.
-
E. Valdinoci, Dislocation dynamics in crystals, Seminari di Analisi Matematica, Università di Torino, Dipartimento di Matematica ``Giuseppe Peano'', Italy, December 18, 2014.
-
E. Valdinoci, Gradient estimates and symmetry results in anisotropic media, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 76: Viscosity, Nonlinearity and Maximum Principle, July 7 - 11, 2014, Madrid, Spain, July 8, 2014.
-
E. Valdinoci, Nonlinear PDEs, Spring School on Nonlinear PDEs, March 24 - 27, 2014, INdAM Istituto Nazionale d'Alta Matematica, Sapienza -- Università di Roma, Italy.
-
E. Valdinoci, Nonlocal equations and applications, Seminario de Ecuaciones Diferenciales, Universidad de Granada, IEMath-Granada, Spain, November 28, 2014.
-
E. Valdinoci, Nonlocal minimal surfaces, The 10th AIMS Conference on Dynamical Systems, Differential Equations and Applications, Special Session 96: Geometric Variational Problems with Associated Stability Estimates, July 7 - 11, 2014, Madrid, Spain, July 8, 2014.
-
E. Valdinoci, Nonlocal minimal surfaces and free boundary problems, Geometric Aspects of Semilinear Elliptic and Parabolic Equations: Recent Advances and Future Perspectives, May 25 - 30, 2014, Banff International Research Station for Mathematical Innovation and Discovery, Calgary, Canada, May 27, 2014.
-
E. Valdinoci, Nonlocal problems in analysis and geometry, December 1 - 5, 2014, Universidad Autonoma de Madrid, Departamento de Matemáticas, Spain.
-
E. Valdinoci, Some nonlocal aspects of partial differential equations and free boundary problems, Institutskolloquium, Weierstrass Institut Berlin (WIAS), January 13, 2014.
-
M.H. Farshbaf Shaker, A deep quench approach to the optimal control of an Allen--Cahn equation with dynamic boundary conditions and double obstacles, Conference on Partial Differential Equations, May 28 - 31, 2014, Novacella, Italy, May 29, 2014.
-
M.H. Farshbaf Shaker, Relating phase field and sharp interface approaches to structural topology optimization, SADCO-WIAS Young Researcher Workshop, January 29 - 31, 2014, WIAS, January 31, 2014.
-
TH. Petzold, On the sharp interface limit of a phase field model with mechanical effects applied to phase transitions in steel, Universität Bremen, Zentrum für Technomathematik, May 22, 2013.
-
O. Klein, Modeling and numerical simulation of the application of traveling magneticfields to stabilize crystal growth from the melt, 12th International Conference on Free Boundary Problems: Theory and Applications, June 11 - 15, 2012, Frauenchiemsee, June 11, 2012.
-
J. Sprekels, A time discretization for a nonstandard viscous Cahn--Hilliard system, INDAM Workshop PDEs for Multiphase Advanced Materials (ADMAT2012), September 17 - 21, 2012, Cortona, Italy, September 19, 2012.
-
J. Sprekels, Mathematical challenges in the industrial growth of semiconductor bulk single crystals, Kick-off Symposium Mathematics: Official Opening of the Felix Klein Building, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, January 13, 2012.
-
K. Götze, Starke Lösungen für die Interaktion von starren Körpern und viskoelastischen Flüssigkeiten, Lectures in Continuum Mechanics, Universität Kassel, Institut für Mathematik, November 7, 2011.
-
J. Sprekels, Mathematical challenges in the industrial growth of semiconductor bulk single crystals, Multiphase and Multiphysics Problems, September 25 - 30, 2011, Riemann International School of Mathematics, Verbania, Italy, September 26, 2011.
-
J. Sprekels, Technical and mathematical problems in the Czochralski growth of single crystals, Workshop ``New Directions in Simulation, Control and Analysis for Interfaces and Free Boundaries'', January 31 - February 6, 2010, Mathematisches Forschungsinstitut Oberwolfach, February 1, 2010.
-
W. Dreyer, Phase transitions and kinetic relations, Séminaire Fluides Compressibles, Université Pierre et Marie Curie, Laboratoire Jacques-Louis Lions, Paris, France, September 30, 2009.
-
W. Dreyer, Phase transitions during hydrogen storage and in lithium-ion batteries, EUROTHERM Seminar no. 84: Thermodynamics of Phase Changes, May 25 - 27, 2009, Université Catholique de Louvain, Namur, Belgium, May 27, 2009.
-
J. Sprekels, Problems in the industrial growth of semiconductor crystals: Radiative transfer, convection, magnetic fields, and free boundaries, Seminar of the Institute of Applied Mathematics and Information Technology, Università di Pavia, Dipartimento di Matematica ``F. Casorati'', Italy, September 23, 2009.
 External Preprints
External Preprints
-
L. Caffarelli, X. Ros-Oton, J. Serra, Obstacle problems for integro-differential operators: Regularity of solutions and free boundaries, Preprint no. arXiv:1601.05843, Cornell University Library, arXiv.org, 2016.
Abstract
We study the obstacle problem for integro-differential operators of order $2s$, with $s in (0; 1)$. Our main results establish the optimal $C^(1;s)$ regularity of solutions $u$, and the $C^(1;alpha)$ regularity of the free boundary near regular points. Namely, we prove the following dichotomy at all free boundary points $x0 in partial u = varphi$: (i) either $u(x) -varphi (x) = c d^(1+s)(x) + o( x - x0 ^(1+s+alpha))$ for some $c > 0$, (ii) or u(x) -varphi(x) = o( x - x0 ^(1+s+alpha))$, where $d$ is the distance to the contact set $u - varphi$. Moreover, we show that the set of free boundary points $x0$ satisfying (i) is open, and that the free boundary is $C^(1;alpha)$ near those points. These results were only known for the fractional Laplacian [CSS08], and are completely new for more general integro-di erential operators. The methods we develop here are purely nonlocal, and do not rely on any monotonicity-type for- mula for the operator. Thanks to this, our techniques can be applied in the much more general context of fully nonlinear integro-di erential operators: we establish similar regularity results for obstacle problems with convex operators. -
X. Ros-Oton, J. Serra, The structure of the free boundary in the fully nonlinear thin obstacle problem, Preprint no. arXiv:1603.09292, Cornell University Library, arXiv.org, 2016.
Abstract
We study the regularity of the free boundary in the fully nonlinear thin obstacle problem. Our main result establishes that the free boundary is C$^1$ near regular points. -
D.A. Gomes, S. Patrizi, Obstacle mean-field game problem, Preprint no. arXiv:1410.6942, Cornell University Library, arXiv.org, 2014.
Abstract
In this paper, we introduce and study a first-order mean-field game obstacle problem. We examine the case of local dependence on the measure under assumptions that include both the logarithmic case and power-like nonlinearities. Since the obstacle operator is not differentiable, the equations for first-order mean field game problems have to be discussed carefully. Hence, we begin by considering a penalized problem. We prove this problem admits a unique solution satisfying uniform bounds. These bounds serve to pass to the limit in the penalized problem and to characterize the limiting equations. Finally, we prove uniqueness of solutions.


