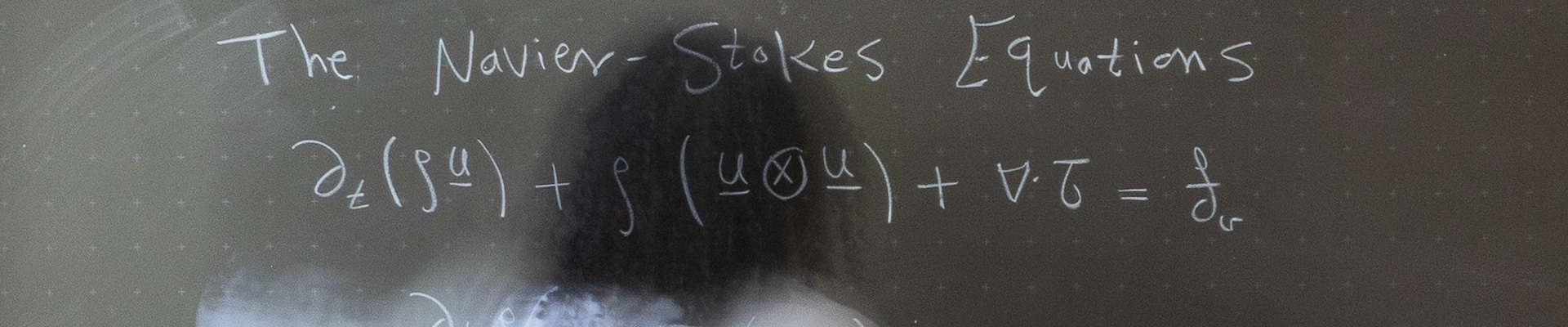A main research field is the development, analysis, improvement and application of numerical methods for equations coming from CFD. The spatial discretization of the equations is based on finite element and finite volume methods. A focus of research is on so-called physically consistent methods, i.e., methods where important physical properties of the continuous problem are transferred to the discrete problem.
Convection-diffusion-reaction equations model, for instance, transport processes which are driven by diffusion or convection. A challenging situation from the point of view of simulations is the case of dominant convection, because the solution has scales which cannot be resolved by the used grids (layers), such that one encounters a multi-scale problem. Standard stabilized methods lead to smeared discrete solutions or to solutions possessing spurious oscillations. Spurious oscillations are not acceptable in many applications. On research topic is the development of oscillation-free numerical methods for convection-dominated equations. This physical consistency property is mathematically characterized with discrete maximum principles, see this paper for a recent survey. In addition, numerical methods for nonlinear transport equations with exponential nonlinearities are developed and analyzed.
The Navier-Stokes equations are the fundamental equations of fluid mechanics. Physical consistency means for the incompressible equations that the discrete solution is divergence-free (exact mass conservation) and that velocity errors do not depend on the pressure (pressure robustness). These properties are not given for many discretizations, e.g., for standard inf-sup stable pairs of finite element spaces like Taylor-Hood pairs. Important approaches for the construction of physically consistent discretizations are described in this SIAM Review paper. The generalization of pressure robustness to compressible problems is the gradient robustness.
Reduced models based on proper orthogonal decompositions (POD-ROMs) result generally in very efficient simulations with acceptable losses of accuracy. Such models are analyzed theoretically and they are used in applications. Possibilities of using techniques of machine learning within the numerical solution of problems with partial differential equations are studied as well.
In the considered applications one has to solve in general coupled problems that contain, among others, the types of equations described above. An example are van Roosbroeck systems that describe the transport of carriers in a semiconductor crystal lattice. The equations of such systems contain exponential nonlinearities. Further applications are from biomedicine (hemodynamics, behavior of organic tissues) and from agriculture.
Publications
 Monographs
Monographs
-
R. Ahrens, Z. Lakdawala, A. Voigt, V. Wiedmeyer, V. John, S. Le Borne, K. Sundmacher, Chapter 14: Numerical Methods for Coupled Population Balance Systems Applied to the Dynamical Simulation of Crystallization Processes, in: Dynamic Flowsheet Simulation of Solids Processes, S. Heinrich, ed., Springer, Cham, 2020, pp. 475--518, (Chapter Published), DOI 10.1007/978-3-030-45168-4_14 .
-
V. John, P. Knobloch, U. Wilbrandt, Chapter 6: Finite Element Pressure Stabilizations for Incompressible Flow Problems, in: Fluids under Pressure, T. Bodnár, G. Galdi, Š. Nečasová, eds., Advances in Mathematical Fluid Mechanics, Birkhäuser, Cham, 2020, pp. 483--573, (Chapter Published), DOI 10.1007/978-3-030-39639-8_6 .
Abstract
Discretizations of incompressible flow problems with pairs of finite element spaces that do not satisfy a discrete inf-sup condition require a so-called pressure stabilization. This paper gives an overview and systematic assessment of stabilized methods, including the respective error analysis. -
U. Wilbrandt, Stokes--Darcy Equations -- Analytic and Numerical Analysis, D. Bresch, V. John, M. Hieber, I. Kukavica, J. Robinson, Y. Shibata, eds., Lecture Notes in Mathematical Fluid Mechanics, Birkhäuser, Basel, 2019, 212 pages, (Monograph Published), DOI 10.1007/978-3-030-02904-3 .
-
M. Hintermüller, M. Hinze, Ch. Kahle, T. Keil, Chapter 13: Fully Adaptive and Integrated Numerical Methods for the Simulation and Control of Variable Density Multiphase Flows Governed by Diffuse Interface Models, in: Transport Processes at Fluidic Interfaces, D. Bothe, A. Reusken, eds., Advances in Mathematical Fluid Mechanics, Birkhäuser, Springer International Publishing AG, Cham, 2017, pp. 305--353, (Chapter Published), DOI 10.1007/978-3-319-56602-3 .
-
V. John, Finite Element Methods for Incompressible Flow Problems, 51 of Springer Series in Computational Mathematics, Springer International Publishing AG, Cham, 2016, xiii+812 pages, (Monograph Published).
-
K. Gärtner, H. Si, A. Rand, N. Walkington, Chapter 11: 3D Delaunay Mesh Generation, in: Combinatorial Scientific Computing, U. Naumann, O. Schenk, eds., Computational Science Series, CRC Computational Science/Chapman & Hall, Boca Raton, 2012, pp. 299--319, (Chapter Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
N. Chamakuri, V. John, N. Ranwan, Finite element analysis of a coupled Navier--Stokes flow - linear elasticity problem, Journal of Mathematical Analysis and Applications, 558 (2026), pp. 130384/1--130384/37, DOI 10.1016/j.jmaa.2025.130384 .
Abstract
A semi-discrete finite element approximation of a fluid-structure interaction problem is analyzed. The fluid part is modeled by the incompressible Navier--Stokes equations. Both the fluid and the solid subdomains are considered to be stationary. In the discretization of the Navier--Stokes equations, a grad-div stabilization term is included, and a special form of the convective term is used. The existence of a finite element solution is shown, a priori estimates are proved, and a finite element error estimate is derived. The dependency of the error bounds on the coefficients of the problem is tracked. Error bounds are obtained whose constants do not depend on the Reynolds number. -
D. Frerichs-Mihov, L. Henning, V. John, On loss functionals for physics-informed neural networks for convection-dominated convection-diffusion problems, Communications on Applied Mathematics and Computation, 8 (2026), pp. 287--308, DOI 10.1007/s42967-024-00433-7 .
Abstract
In the convection-dominated regime, solutions of convection-diffusion problems usually possesses layers, which are regions where the solution has a steep gradient. It is well known that many classical numerical discretization techniques face difficulties when approximating the solution to these problems. In recent years, physics-informed neural networks (PINNs) for approximating the solution to (initial-)boundary value problems received a lot of interest. In this work, we study various loss functionals for PINNs that are novel in the context of PINNs and are especially designed for convection-dominated convection-diffusion problems. They are numerically compared to the vanilla and a $hp$-variational loss functional from the literature based on two benchmark problems whose solutions possess different types of layers. We observe that the best novel loss functionals reduce the $L^2(Omega)$ error by $17.3%$ for the first and $5.5%$ for the second problem compared to the methods from the literature. -
B. García-Archilla, V. John, J. Novo, POD-ROM methods: From a finite set of snapshots to continuous-in-time approximations, SIAM Journal on Numerical Analysis, 63 (2025), pp. 800-826, DOI 10.1137/24M1645681 .
Abstract
This paper studies discretization of time-dependent partial differential equations (PDEs) by proper orthogonal decomposition reduced order models (POD-ROMs). Most of the analysis in the literature has been performed on fully discrete methods using first order methods in time, typically the implicit Euler time integrator. Our aim is to show which kind of error bounds can be obtained using any time integrator, both in the full order model (FOM), applied to compute the snapshots, and in the POD-ROM method. To this end, we analyze in this paper the continuous-in-time case for both the FOM and POD-ROM methods, although the POD basis is obtained from snapshots taken at a discrete (i.e., not continuous) set of times. Two cases for the set of snapshots are considered: the case in which the snapshots are based on first order divided differences in time and the case in which they are based on temporal derivatives. Optimal pointwise-in-time error bounds between the FOM and the POD-ROM solutions are proved for the L high 2 (omega) norm of the error for a semilinear reaction-diffusion model problem. The dependency of the errors on the distance in time between two consecutive snapshots and on the tail of the POD eigenvalues is tracked. Our detailed analysis allows us to show that, in some situations, a small number of snapshots in a given time interval might be sufficient to accurately approximate the solution in the full interval. Numerical studies support the error analysis. -
V. John, Ch. Merdon, M. Zainelabdeen, Augmenting the grad-div stabilization for Taylor--Hood finite elements with a vorticity stabilization, Journal of Numerical Mathematics, 33 (2025), pp. 37--54, DOI 10.1515/jnma-2023-0118 .
Abstract
The least squares vorticity stabilization (LSVS), proposed in Ahmed et al. for the Scott--Vogelius finite element discretization of the Oseen equations, is studied as an augmentation of the popular grad-div stabilized Taylor--Hood pair of spaces. An error analysis is presented which exploits the situation that the velocity spaces of Scott--Vogelius and Taylor--Hood are identical. Convection-robust error bounds are derived under the assumption that the Scott--Vogelius discretization is well posed on the considered grid. Numerical studies support the analytic results and they show that the LSVS-grad-div method might lead to notable error reductions compared with the standard grad-div method. -
F. Romor, G. Stabile, G. Rozza, Explicable hyper-reduced order models on nonlinearly approximated solution manifolds of compressible and incompressible Navier--Stokes equations, Journal of Computational Physics, 524 (2025), pp. 113729/1--113729/8, DOI 10.1016/j.jcp.2025.113729 .
Abstract
A slow decaying Kolmogorov n-width of the solution manifold of a parametric partial differential equation precludes the realization of efficient linear projection-based reduced-order models. This is due to the high dimensionality of the reduced space needed to approximate with sufficient accuracy the solution manifold. To solve this problem, neural networks, in the form of different architectures, have been employed to perform accurate nonlinear regressions of the solution manifolds. However, the majority of the implementations are non-intrusive black-box surrogate models and only a part of them perform dimension reduction from the number of degrees of freedom of the discretized parametric models to a latent dimension. We present a new intrusive and explicable methodology for reduced-order modeling that employs neural networks for the solution manifold approximation but that does not discard the physical and numerical models underneath in the predictive/online stage. We will focus on autoencoders used to compress further the dimensionality of linear approximants of solution manifolds, achieving in the end a nonlinear dimension reduction. After having obtained an accurate nonlinear approximant, we seek for the solutions on the latent manifold with the residual-based nonlinear least-squares Petrov--Galerkin method, opportunely hyper-reduced in order to be independent of the number of degrees of freedom. New adaptive hyper-reduction strategies are developed along with the employment of local nonlinear approximants. We test our methodology on two nonlinear time dependent parametric benchmarks involving a supersonic flow past a NACA airfoil with changing Mach number and an incompressible turbulent flow around the Ahmed body with changing slant angle. -
N. Ahmed, V. John, X. Li, Ch. Merdon, Inf-sup stabilized Scott--Vogelius pairs on general shape-regular simplicial grids for Navier--Stokes equations, Computers & Mathematics with Applications. An International Journal, 168 (2024), pp. 148--161, DOI 10.1016/j.camwa.2024.05.034 .
Abstract
This paper considers the discretization of the time-dependent Navier--Stokes equations with the family of inf-sup stabilized Scott--Vogelius pairs recently introduced in [John/Li/Merdon/Rui, Math. Models Methods Appl. Sci., 2024] for the Stokes problem. Therein, the velocity space is obtained by enriching the H -conforming Lagrange element space with some H (div)-conforming Raviart--Thomas functions, such that the divergence constraint is satisfied exactly. In these methods arbitrary shape-regular simplicial grids can be used. In the present paper two alternatives for discretizing the convective terms are considered. One variant leads to a scheme that still only involves volume integrals, and the other variant employs upwinding known from DG schemes. Both variants ensure the conservation of linear momentum and angular momentum in some suitable sense. In addition, a pressure-robust and convection-robust velocity error estimate is derived, i.e., the velocity error bound does not depend on the pressure and the constant in the error bound for the kinetic energy does not blow up for small viscosity. After condensation of the enrichment unknowns and all non-constant pressure unknowns, the method can be reduced to a P - P -like system for arbitrary velocity polynomial degree k. Numerical studies verify the theoretical findings. -
R. Araya, A. Caiazzo, F. Chouly, Stokes problem with slip boundary conditions using stabilized finite elements combined with Nitsche, Computer Methods in Applied Mechanics and Engineering, 427 (2024), pp. 117037/1--117037/16, DOI 10.1016/j.cma.2024.117037 .
Abstract
We discuss how slip conditions for the Stokes equation can be handled using Nitsche method, for a stabilized finite element discretization. Emphasis is made on the interplay between stabilization and Nitsche terms. Well-posedness of the discrete problem and optimal convergence rates, in natural norm for the velocity and the pressure, are established, and illustrated with various numerical experiments. The proposed method fits naturally in the context of a finite element implementation while being accurate, and allows an increased flexibility in the choice of the finite element pairs. -
G.R. Barrenechea, V. John, P. Knobloch, Finite element methods respecting the discrete maximum principle for convection-diffusion equations, SIAM Review, 66 (2024), pp. 3--88, DOI 10.1137/22M1488934 .
Abstract
Convection-diffusion-reaction equations model the conservation of scalar quantities. From the analytic point of view, solutions of these equations satisfy, under certain conditions, maximum principles, which represent physical bounds of the solution. That the same bounds are respected by numerical approximations of the solution is often of utmost importance in practice. The mathematical formulation of this property, which contributes to the physical consistency of a method, is called the discrete maximum principle (DMP). In many applications, convection dominates diffusion by several orders of magnitude. It is well known that standard discretizations typically do not satisfy the DMP in this convection-dominated regime. In fact, in this case it turns out to be a challenging problem to construct discretizations that, on the one hand, respect the DMP and, on the other hand, compute accurate solutions. This paper presents a survey on finite element methods, with the main focus on the convection-dominated regime, that satisfy a local or a global DMP. The concepts of the underlying numerical analysis are discussed. The survey reveals that for the steady-state problem there are only a few discretizations, all of them nonlinear, that at the same time both satisfy the DMP and compute reasonably accurate solutions, e.g., algebraically stabilized schemes. Moreover, most of these discretizations have been developed in recent years, showing the enormous progress that has been achieved lately. Similarly, methods based on algebraic stabilization, both nonlinear and linear, are currently the only finite element methods that combine the satisfaction of the global DMP and accurate numerical results for the evolutionary equations in the convection-dominated scenario. -
B. García-Archilla , V. John, S. Katz, J. Novo, POD-ROMs for incompressible flows including snapshots of the temporal derivative of the full order solution: Error bounds for the pressure, Journal of Numerical Mathematics, 32 (2024), pp. 301--329, DOI 10.1515/jnma-2023-0039 .
Abstract
Reduced order methods (ROMs) for the incompressible Navier?Stokes equations, based on proper orthogonal decomposition (POD), are studied that include snapshots which approach the temporal derivative of the velocity from a full order mixed finite element method (FOM). In addition, the set of snapshots contains the mean velocity of the FOM. Both the FOM and the POD-ROM are equipped with a grad-div stabilization. A velocity error analysis for this method can be found already in the literature. The present paper studies two different procedures to compute approximations to the pressure and proves error bounds for the pressure that are independent of inverse powers of the viscosity. Numerical studies support the analytic results and compare both methods. -
C. Cárcamo, A. Caiazzo, F. Galarce, J. Mura, A stabilized total pressure-formulation of the Biot's poroelasticity equations in frequency domain: Numerical analysis and applications, Computer Methods in Applied Mechanics and Engineering, 432 (2024), pp. 117353/1--117353/31, DOI 10.1016/j.cma.2024.117353 .
Abstract
This work focuses on the numerical solution of the dynamics of a poroelastic material in the frequency domain. We provide a detailed stability analysis based on the application of the Fredholm alternative in the continuous case, considering a total pressure formulation of the Biot's equations. In the discrete setting, we propose a stabilized equal order finite element method complemented by an additional pressure stabilization to enhance the robustness of the numerical scheme with respect to the fluid permeability. Utilizing the Fredholm alternative, we extend the well-posedness results to the discrete setting, obtaining theoretical optimal convergence for the case of linear finite elements. We present different numerical experiments to validate the proposed method. First, we consider model problems with known analytic solutions in two and three dimensions. As next, we show that the method is robust for a wide range of permeabilities, including the case of discontinuous coefficients. Lastly, we show the application for the simulation of brain elastography on a realistic brain geometry obtained from medical imaging. -
V. John, X. Li, Ch. Merdon, H. Rui, Inf-sup stabilized Scott--Vogelius pairs on general simplicial grids by Raviart--Thomas enrichment, Mathematical Models & Methods in Applied Sciences, 34 (2024), pp. 919--949, DOI 10.1142/S0218202524500180 .
Abstract
This paper considers the discretization of the Stokes equations with Scott--Vogelius pairs of finite element spaces on arbitrary shape-regular simplicial grids. A novel way of stabilizing these pairs with respect to the discrete inf-sup condition is proposed and analyzed. The key idea consists in enriching the continuous polynomials of order k of the Scott--Vogelius velocity space with appropriately chosen and explicitly given Raviart--Thomas bubbles. This approach is inspired by [Li/Rui, IMA J. Numer. Anal, 2021], where the case k=1 was studied. The proposed method is pressure-robust, with optimally converging H1-conforming velocity and a small H(div)-conforming correction rendering the full velocity divergence-free. For k>d, with d being the dimension, the method is parameter-free. Furthermore, it is shown that the additional degrees of freedom for the Raviart--Thomas enrichment and also all non-constant pressure degrees of freedom can be condensated, effectively leading to a pressure-robust, inf-sup stable, optimally convergent Pk×P0 scheme. Aspects of the implementation are discussed and numerical studies confirm the analytic results. -
V. John, X. Li, Ch. Merdon, Pressure-robust $L^2 (Omega)$ error analysis for Raviart--Thomas enriched Scott--Vogelius pairs, Applied Mathematics Letters, 156 (2024), pp. 109138/1--109138/12, DOI 10.1016/j.aml.2024.109138 .
Abstract
Recent work shows that it is possible to enrich the Scott--Vogelius finite element pair by cer- tain Raviart--Thomas functions to obtain an inf-sup stable and divergence-free method on general shape-regular meshes. A skew-symmetric consistency term was suggested for avoiding an ad- ditional stabilization term for higher order elements, but no L2 (Ω) error estimate was shown for the Stokes equations. This note closes this gap. In addition, the optimal choice of the stabilization parameter is studied numerically. -
V. John, Ch. Merdon, M. Zainelabdeen, Augmenting the grad-div stabilization for Taylor--Hood finite elements with a vorticity stabilization, Journal of Numerical Mathematics, published online on 05.11.2024, DOI 10.1515/jnma-2023-0118 .
Abstract
The least squares vorticity stabilization (LSVS), proposed in Ahmed et al. for the Scott--Vogelius finite element discretization of the Oseen equations, is studied as an augmentation of the popular grad-div stabilized Taylor--Hood pair of spaces. An error analysis is presented which exploits the situation that the velocity spaces of Scott--Vogelius and Taylor--Hood are identical. Convection-robust error bounds are derived under the assumption that the Scott--Vogelius discretization is well posed on the considered grid. Numerical studies support the analytic results and they show that the LSVS-grad-div method might lead to notable error reductions compared with the standard grad-div method. -
S. Katz, A. Caiazzo, V. John, Impact of viscosity modeling on the simulation of aortic blood flow, Journal of Computational and Applied Mathematics, 425 (2023), pp. 115036/1--115036/18, DOI 10.1016/j.cam.2022.115036 .
Abstract
Modeling issues for the simulation of blood flow in an aortic coarctation are studied in this paper. From the physical point of view, several viscosity models for non-Newtonian fluids as well as a Newtonian fluid model will be considered. From the numerical point of view, two different turbulence models are utilized in the simulations. The impact of both, the physical and the numerical modeling, on clinically relevant biomarkers is investigated and compared. -
S. Katz, A. Caiazzo, B. Moreau, U. Wilbrandt, J. Brüning, L. Goubergrits, V. John, Impact of turbulence modeling on the simulation of blood flow in aortic coarctation, International Journal of Numerical Methods in Biomedical Engineering, 39 (2023), pp. e3695/1--e3695/36, DOI 10.1002/cnm.3695 .
Abstract
Numerical simulations of pulsatile blood flow in an aortic coarctation require the use of turbulence modeling. This paper considers three models from the class of large eddy simulation (LES) models (Smagorinsky, Vreman, -model) and one model from the class of variational multiscale models (residual-based) within a finite element framework. The influence of these models on the estimation of clinically relevant biomarkers used to assess the degree of severity of the pathological condition (pressure difference, secondary flow degree, normalized flow displacement, wall shear stress) is investigated in detail. The simulations show that most methods are consistent in terms of severity indicators such as pressure difference and stenotic velocity. Moreover, using second-order velocity finite elements, different turbulence models might lead to considerably different results concerning other clinically relevant quantities such as wall shear stresses. These differences may be attributed to differences in numerical dissipation introduced by the turbulence models. -
F. Galarce Marín, K. Tabelow, J. Polzehl, Ch.P. Papanikas, V. Vavourakis, L. Lilaj, I. Sack, A. Caiazzo, Displacement and pressure reconstruction from magnetic resonance elastography images: Application to an in silico brain model, SIAM Journal on Imaging Sciences, 16 (2023), pp. 996--1027, DOI 10.1137/22M149363X .
Abstract
This paper investigates a data assimilation approach for non-invasive quantification of intracranial pressure from partial displacement data, acquired through magnetic resonance elastography. Data assimilation is based on a parametrized-background data weak methodology, in which the state of the physical system tissue displacements and pressure fields is reconstructed from partially available data assuming an underlying poroelastic biomechanics model. For this purpose, a physics-informed manifold is built by sampling the space of parameters describing the tissue model close to their physiological ranges, to simulate the corresponding poroelastic problem, and compute a reduced basis. Displacements and pressure reconstruction is sought in a reduced space after solving a minimization problem that encompasses both the structure of the reduced-order model and the available measurements. The proposed pipeline is validated using synthetic data obtained after simulating the poroelastic mechanics on a physiological brain. The numerical experiments demonstrate that the framework can exhibit accurate joint reconstructions of both displacement and pressure fields. The methodology can be formulated for an arbitrary resolution of available displacement data from pertinent images. It can also inherently handle uncertainty on the physical parameters of the mechanical model by enlarging the physics-informed manifold accordingly. Moreover, the framework can be used to characterize, in silico, biomarkers for pathological conditions, by appropriately training the reduced-order model. A first application for the estimation of ventricular pressure as an indicator of abnormal intracranial pressure is shown in this contribution. -
D. Budáč, V. Miloš, M. Carda, M. Paidar, J. Fuhrmann, K. Bouzek, Prediction of electrical conductivity of porous composites using a simplified Monte Carlo 3D equivalent electronic circuit network model: LSM--YSZ case study, Electrochimica Acta, 457 (2023), pp. 142512/1--142512/12, DOI 10.1016/j.electacta.2023.142512 .
Abstract
Multiphase electric charge conductors composed of materials with various properties are widely utilized in both research and industrial applications. The composite materials include porous electrodes and other components mainly applied in fuel cell and battery technologies. In this study, a simplified Monte Carlo equivalent electronic circuit (EEC) network model is presented. In comparison to similar models, the present EEC network model allows an accurate prediction of the electrical properties of such materials, thus saving time-consuming experimental determination. The distinct feature of this EEC network model is that it requires only experimentally easily obtainable data as the input parameters: phase composition, porosity and bulk electrical conductivity of the individual constituents. During its run, the model generates a large number of artificial cubically shaped specimens based on random distribution of individual phases according to the input composition. Each of the specimens generated was modelled by a corresponding EEC network. The EEC networks were solved using Kirchhoff's laws, resulting in impedance response simulation for the prediction of composite conductivity values. The EEC network model was validated using lanthanum strontium manganite mixed with yttria-stabilized zirconia. Excellent agreement was obtained between the experimentally determined and the calculated electrical conductivity for sample porosities of 0 to 60 %. Due to its variability, the EEC network model can be suitable for a wide range of practical applications. The presented approach has high potential to save an enormous amount of experimental effort, while maintaining sufficient accuracy, when designing corresponding multiphase electrode structures. -
B. García-Archilla, V. John, J. Novo, Second order error bounds for POD-ROM methods based on first order divided differences, Applied Mathematics Letters, 146 (2023), pp. 108836/1--108836/7, DOI 10.1016/j.aml.2023.108836 .
Abstract
This note proves for the heat equation that using BDF2 as time stepping scheme in POD-ROM methods with snapshots based on difference quotients gives both the optimal second order error bound in time and pointwise estimates. -
B. García-Archilla, V. John, J. Novo, POD-ROMs for incompressible flows including snapshots of the temporal derivative of the full order solution, SIAM Journal on Numerical Analysis, 61 (2023), pp. 1340--1368, DOI 10.1137/22M1503853 .
Abstract
In this paper we study the influence of including snapshots that approach the velocity time derivative in the numerical approximation of the incompressible Navier--Stokes equations by means of proper orthogonal decomposition (POD) methods. Our set of snapshots includes the velocity approximation at the initial time from a full order mixed finite element method (FOM) together with approximations to the time derivative at different times. The approximation at the initial velocity can be replaced by the mean value of the velocities at the different times so that when implementing the method to the fluctuations, as done mostly in practice, only approximations to the time derivatives are included in the set of snapshots. For the POD method we study the differences between projecting onto L2 and H1. In both cases pointwise in time error bounds can be proved. Including grad-div stabilization in both the FOM and the POD methods, error bounds with constants independent of inverse powers of the viscosity can be obtained. -
A. Jha, V. John, P. Knobloch, Adaptive grids in the context of algebraic stabilizations for convection-diffusion-reaction equations, SIAM Journal on Scientific Computing, 45 (2023), pp. B564--B589, DOI 10.1137/21M1466360 .
Abstract
Three algebraically stabilized finite element schemes for discretizing convection-diffusion-reaction equations are studied on adaptively refined grids. These schemes are the algebraicflux correction (AFC) scheme with the Kuzmin limiter, the AFC scheme with the Barrenechea-John-Knobloch limiter, and the recently proposed monotone upwind--type algebraically stabilizedmethod. Both conforming closure of the refined grids and grids with hanging vertices are considered.A nonstandard algorithmic step becomes necessary before these schemes can be applied on gridswith hanging vertices. The assessment of the schemes is performed with respect to the satisfactionof the global discrete maximum principle, the accuracy, e.g., smearing of layers, and the efficiency insolving the corresponding nonlinear problems. -
A. Jha, O. Pártl, N. Ahmed, D. Kuzmin, An assessment of solvers for algebraically stabilized discretizations of convection-diffusion-reaction equations, Journal of Numerical Mathematics, 31 (2023), pp. 79--103, DOI 10.1515/jnma-2021-0123 .
Abstract
We consider flux-corrected finite element discretizations of 3D convection-dominated transport problems and assess the computational efficiency of algorithms based on such approximations. The methods under investigation include flux-corrected transport schemes and monolithic limiters. We discretize in space using a continuous Galerkin method and P1 or Q1 finite elements. Time integration is performed using the Crank-Nicolson method or an explicit strong stability preserving Runge-Kutta method. Nonlinear systems are solved using a fixed-point iteration method, which requires solution of large linear systems at each iteration or time step. The great variety of options in the choice of discretization methods and solver components calls for a dedicated comparative study of existing approaches. To perform such a study, we define new 3D test problems for time dependent and stationary convection-diffusion-reaction equations. The results of our numerical experiments illustrate how the limiting technique, time discretization and solver impact on the overall performance. -
D. Frerichs-Mihov, L. Henning, V. John, Using deep neural networks for detecting spurious oscillations in discontinuous Galerkin solutions of convection-dominated convection-diffusion equations, Journal of Scientific Computing, 97 (2023), pp. 36/1--36/27, DOI 10.1007/s10915-023-02335-x .
Abstract
Standard discontinuous Galerkin (DG) finite element solutions to convection-dominated convection-diffusion equations usually possess sharp layers but also exhibit large spurious oscillations. Slope limiters are known as a post-processing technique to reduce these unphysical values. This paper studies the application of deep neural networks for detecting mesh cells on which slope limiters should be applied. The networks are trained with data obtained from simulations of a standard benchmark problem with linear finite elements. It is investigated how they perform when applied to discrete solutions obtained with higher order finite elements and to solutions for a different benchmark problem. -
V. John, P. Knobloch, U. Wilbrandt, A posteriori optimization of parameters in stabilized methods for convection-diffusion problems -- Part II, Journal of Computational and Applied Mathematics, 428 (2023), pp. 115167/1--115167/17, DOI 10.1016/j.cam.2023.115167 .
Abstract
Extensions of algorithms for computing optimal stabilization parameters in finite element methods for convection-diffusion equations are presented. These extensions reduce the dimension of the control space, in comparison to available methods, and thus address the long computing times of these methods. One method is proposed that considers only relevant mesh cells, another method that uses groups of mesh cells, and the combination of both methods is also studied. The incorporation of these methods within a gradient-based optimization procedure, via solving an adjoint problem, is explained. Numerical studies provide impressions on the gain of efficiency as well as on the loss of accuracy if control spaces with reduced dimensions are utilized. -
R. Lasarzik, M.E.V. Reiter, Analysis and numerical approximation of energy-variational solutions to the Ericksen--Leslie equations, Acta Applicandae Mathematicae. An International Survey Journal on Applying Mathematics and Mathematical Applications, 184 (2023), pp. 11/1--11/44, DOI 10.1007/s10440-023-00563-9 .
Abstract
We define the concept of energy-variational solutions for the Ericksen--Leslie equations in three spatial dimensions. This solution concept is finer than dissipative solutions and satisfies the weak-strong uniqueness property. For a certain choice of the regularity weight, the existence of energy-variational solutions implies the existence of measure-valued solutions and for a different choice, we construct an energy-variational solution with the help of an implementable, structure-inheriting space-time discretization. Computational studies are performed in order to provide some evidence of the applicability of the proposed algorithm. -
CH. Merdon, W. Wollner, Pressure-robustness in the context of optimal control, SIAM Journal on Control and Optimization, 61 (2023), pp. 342--360, DOI 10.1137/22M1482603 .
Abstract
This paper studies the benefits of pressure-robust discretizations in the scope of optimal control of incompressible flows. Gradient forces that may appear in the data can have a negative impact on the accuracy of state and control and can only be correctly balanced if their L2-orthogonality onto discretely divergence-free test functions is restored. Perfectly orthogonal divergence-free discretizations or divergence-free reconstructions of these test functions do the trick and lead to much better analytic a priori estimates that are also validated in numerical examples. -
P. Vágner, M. Pavelka, J. Fuhrmann, V. Klika, A multiscale thermodynamic generalization of Maxwell--Stefan diffusion equations and of the dusty gas model, International Journal of Heat and Mass Transfer, 199 (2022), pp. 123405/1--123405/14, DOI 10.1016/j.ijheatmasstransfer.2022.123405 .
Abstract
Despite the fact that the theory of mixtures has been part of non-equilibrium thermodynamics and engineering for a long time, it is far from complete. While it is well formulated and tested in the case of mechanical equilibrium (where only diffusion-like processes take place), the question how to properly describe homogeneous mixtures that flow with multiple independent velocities that still possess some inertia (before mechanical equilibrium is reached) is still open. Moreover, the mixtures can have several temperatures before they relax to a common value. In this paper, we derive a theory of mixtures from Hamiltonian mechanics in interaction with electromagnetic fields. The resulting evolution equations are then reduced to the case with only one momentum (classical irreversible thermodynamics), providing a generalization of the Maxwell-Stefan diffusion equations. In a next step, we reduce that description to the mechanical equilibrium (no momentum) and derive a non-isothermal variant of the dusty gas model. These reduced equations are solved numerically, and we illustrate the results on effciency analysis, showing where in a concentration cell effciency is lost. Finally, the theory of mixtures identifies the temperature difference between constituents as a possible new source of the Soret coeffcient. For the sake of clarity, we restrict the presentation to the case of binary mixtures; the generalization is straightforward. -
M. Coghi, W. Dreyer, P.K. Friz, P. Gajewski, C. Guhlke, M. Maurelli, A McKean--Vlasov SDE and particle system with interaction from reflecting boundaries, SIAM Journal on Mathematical Analysis, 54 (2022), pp. 2251--2294, DOI 10.1137/21M1409421 .
-
D. Frerichs-Mihov, V. John, On a technique for reducing spurious oscillations in DG solutions of convection-diffusion equations, Applied Mathematics Letters, 129 (2022), pp. 107969/1--107969/7, DOI 10.1016/j.aml.2022.107969 .
Abstract
This note studies a generalization of a post-processing technique and a novel method inspired by the same technique which significantly reduce spurious oscillations in discontinuous Galerkin solutions of convection-diffusion equations in the convection-dominated regime. -
V. John, P. Knobloch, O. Pártl, A numerical assessment of finite element discretizations for convection-diffusion-reaction equations satisfying discrete maximum principles, Computational Methods in Applied Mathematics, 23 (2023), pp. 969--988 (published online on 30.09.2022), DOI 10.1515/cmam-2022-0125 .
Abstract
Numerical studies are presented that investigate finite element methods satisfying discrete maximum principles for convection-diffusion-reaction equations. Two linear methods and several nonlinear schemes, some of them proposed only recently, are included in these studies, which consider a number of two-dimensional examples. The evaluation of the results examines the accuracy of the numerical solutions with respect to quantities of interest, like layer widths, and the efficiency of the simulations. -
V. John, P. Knobloch, On algebraically stabilized schemes for convection-diffusion-reaction problems, Numerische Mathematik, 152 (2022), pp. 553--585, DOI 10.1007/s00211-022-01325-9 .
-
V. John, B. Moreau, J. Novo, Error analysis of a SUPG-stabilized POD-ROM method for convection-diffusion-reaction equations, Computers & Mathematics with Applications. An International Journal, 122 (2022), pp. 48--60, DOI 10.1016/j.camwa.2022.07.017 .
Abstract
A reduced order model (ROM) method based on proper orthogonal decomposition (POD) is analyzed for convection-diffusion-reaction equations. The streamline-upwind Petrov--Galerkin (SUPG) stabilization is used in the practically interesting case of dominant convection, both for the full order method (FOM) and the ROM simulations. The asymptotic choice of the stabilization parameter for the SUPG-ROM is done as proposed in the literature. This paper presents a finite element convergence analysis of the SUPG-ROM method for errors in different norms. The constants in the error bounds are uniform with respect to small diffusion coefficients. Numerical studies illustrate the performance of the SUPG-ROM method. -
D. Abdel, P. Vágner, J. Fuhrmann, P. Farrell, Modelling charge transport in perovskite solar cells: Potential-based and limiting ion depletion, Electrochimica Acta, 390 (2021), pp. 138696/1--138696/12, DOI 10.1016/j.electacta.2021.138696 .
Abstract
From Maxwell--Stefan diffusion and general electrostatics, we derive a drift-diffusion model for charge transport in perovskite solar cells (PSCs) where any ion in the perovskite layer may flexibly be chosen to be mobile or immobile. Unlike other models in the literature, our model is based on quasi Fermi potentials instead of densities. This allows to easily include nonlinear diffusion (based on Fermi--Dirac, Gauss--Fermi or Blakemore statistics for example) as well as limit the ion depletion (via the Fermi--Dirac integral of order-1). The latter will be motivated by a grand-canonical formalism of ideal lattice gas. Furthermore, our model allows to use different statistics for different species. We discuss the thermodynamic equilibrium, electroneutrality as well as generation/recombination. Finally, we present numerical finite volume simulations to underline the importance of limiting ion depletion. -
L. Lilaj, H. Harthum, T. Meyer, M. Shahrayari, G. Bertalan, A. Caiazzo, J. Braun, Th. Fischer, S. Hirsch, I. Sack, Inversion-recovery MR elastography of the human brain for improved stiffness quantification near fluid-solid boundaries, Magnetic Resonance in Medicine, (2021), published online on 28.06.2021, DOI 10.1002/mrm.28898 .
-
N. Ahmed, G.R. Barrenechea, E. Burman, J. Guzmán, A. Linke, Ch. Merdon, A pressure-robust discretization of Oseen's equation using stabilization in the vorticity equation, SIAM Journal on Numerical Analysis, 59 (2021), pp. 2746--2774, DOI 10.1137/20M1351230 .
Abstract
Discretization of Navier--Stokes' equations using pressure-robust finite element methods is considered for the high Reynolds number regime. To counter oscillations due to dominating convection we add a stabilization based on a bulk term in the form of a residual-based least squares stabilization of the vorticity equation supplemented by a penalty term on (certain components of) the gradient jump over the elements faces. Since the stabilization is based on the vorticity equation, it is independent of the pressure gradients, which makes it pressure-robust. Thus, we prove pressureindependent error estimates in the linearized case, known as Oseen's problem. In fact, we prove an O(hk+1/2) error estimate in the L2-norm that is known to be the best that can be expected for this type of problem. Numerical examples are provided that, in addition to confirming the theoretical results, show that the present method compares favorably to the classical residual-based SUPG stabilization. -
TH. Apel, V. Kempf, A. Linke, Ch. Merdon, A nonconforming pressure-robust finite element method for the Stokes equations on anisotropic meshes, IMA Journal of Numerical Analysis, 42 (2022), pp. 392--416 (published online on 14.01.2021), DOI 10.1093/imanum/draa097 .
Abstract
Most classical finite element schemes for the (Navier--)Stokes equations are neither pressure-robust, nor are they inf-sup stable on general anisotropic triangulations. A lack of pressure-robustness may lead to large velocity errors, whenever the Stokes momentum balance is dominated by a strong and complicated pressure gradient. It is a consequence of a method, which does not exactly satisfy the divergence constraint. However, inf-sup stable schemes can often be made pressure-robust just by a recent, modified discretization of the exterior forcing term, using H(div)-conforming velocity reconstruction operators. This approach has so far only been analyzed on shape-regular triangulations. The novelty of the present contribution is that the reconstruction approach for the Crouzeix--Raviart method, which has a stable Fortin operator on arbitrary meshes, is combined with results on the interpolation error on anisotropic elements for reconstruction operators of Raviart--Thomas and Brezzi--Douglas--Marini type, generalizing the method to a large class of anisotropic triangulations. Numerical examples confirm the theoretical results in a 2D and a 3D test case. -
L. Baňas, R. Lasarzik, A. Prohl, Numerical analysis for nematic electrolytes, IMA Journal of Numerical Analysis, 41 (2021), pp. 2186--2254, DOI 10.1093/imanum/draa082 .
Abstract
We consider a system of nonlinear PDEs modeling nematic electrolytes, and construct a dissipative solution with the help of its implementable, structure-inheriting space-time discretization. Computational studies are performed to study the mutual effects of electric, elastic, and viscous effects onto the molecules in a nematic electrolyte. -
B. García-Archilla, V. John, J. Novo, On the convergence order of the finite element error in the kinetic energy for high Reynolds number incompressible flows, Computer Methods in Applied Mechanics and Engineering, 385 (2021), pp. 114032/1--114032/54, DOI 10.1016/j.cma.2021.114032 .
-
L. Heltai, A. Caiazzo, L.O. Müller, Multiscale coupling of one-dimensional vascular models and elastic tissues, Annals of Biomedical Engineering (ABME), published online on 20.07.2021, DOI 10.1007/s10439-021-02804-0 .
Abstract
We present a computational multiscale model for the efficient simulation of vascularized tissues, composed of an elastic three-dimensional matrix and a vascular network. The effect of blood vessel pressure on the elastic tissue is surrogated via hyper-singular forcing terms in the elasticity equations, which depend on the fluid pressure. In turn, the blood flow in vessels is treated as a one-dimensional network. The pressure and velocity of the blood in the vessels are simulated using a high-order finite volume scheme, while the elasticity equations for the tissue are solved using a finite element method. This work addresses the feasibility and the potential of the proposed coupled multiscale model. In particular, we assess whether the multiscale model is able to reproduce the tissue response at the effective scale (of the order of millimeters) while modeling the vasculature at the microscale. We validate the multiscale method against a full scale (three-dimensional) model, where the fluid/tissue interface is fully discretized and treated as a Neumann boundary for the elasticity equation. Next, we present simulation results obtained with the proposed approach in a realistic scenario, demonstrating that the method can robustly and efficiently handle the one-way coupling between complex fluid microstructures and the elastic matrix. -
P.L. Lederer, Ch. Merdon, Guaranteed upper bounds for the velocity error of pressure-robust Stokes discretisations, Journal of Numerical Mathematics, published online on 6.11.2021, DOI https://doi.org/10.1515/jnma-2021-0078 .
Abstract
This paper improves guaranteed error control for the Stokes problem with a focus on pressure-robustness, i.e. for discretisations that compute a discrete velocity that is independent of the exact pressure. A Prager-Synge type result relates the errors of divergence-free primal and H(div)-conforming dual mixed methods (for the velocity gradient) with an equilibration constraint that needs special care when discretised. To relax the constraints on the primal and dual method, a more general result is derived that enables the use of a recently developed mass conserving mixed stress discretisation to design equilibrated fluxes that yield pressure-independent guaranteed upper bounds for any pressure-robust (but not necessarily divergence-free) primal discretisation. Moreover, a provably efficient local design of the equilibrated fluxes is presented that reduces the numerical costs of the error estimator. All theoretical findings are verified by numerical examples which also show that the efficiency indices of our novel guaranteed upper bounds for the velocity error are close to 1. -
D. Frerichs, V. John, On reducing spurious oscillations in discontinuous Galerkin (DG) methods for steady-state convection-diffusion equations, Journal of Computational and Applied Mathematics, 393 (2021), pp. 113487/1--113487/20, DOI 10.1016/j.cam.2021.113487 .
-
U. Wilbrandt, N. Alia, V. John, Optimal control of a buoyancy-driven liquid steel stirring modeled with single-phase Navier--Stokes equations, Journal of Mathematics in Industry, 11 (2021), pp. 10/1--10/22, DOI 10.1186/s13362-021-00106-7 .
Abstract
Gas stirring is an important process used in secondary metallurgy. It allows to homogenize the temperature and the chemical composition of the liquid steel and to remove inclusions which can be detrimental for the end-product quality. In this process, argon gas is injected from two nozzles at the bottom of the vessel and rises by buoyancy through the liquid steel thereby causing stirring, i.e., a mixing of the bath. The gas flow rates and the positions of the nozzles are two important control parameters in practice. A continuous optimization approach is pursued to find optimal values for these control variables. The effect of the gas appears as a volume force in the single-phase incompressible NavierStokes equations. Turbulence is modeled with the Smagorinsky Large Eddy Simulation (LES) model. An objective functional based on the vorticity is used to describe the mixing in the liquid bath. Optimized configurations are compared with a default one whose design is based on a setup from industrial practice. -
M. Akbas, Th. Gallouët, A. Gassmann, A. Linke, Ch. Merdon, A gradient-robust well-balanced scheme for the compressible isothermal Stokes problem, Computer Methods in Applied Mechanics and Engineering, 367 (2020), pp. 113069/1--113069/25, DOI 10.1016/j.cma.2020.113069 .
Abstract
A novel notion for constructing a well-balanced scheme --- a gradient-robust scheme --- is introduced and a showcase application for a steady compressible, isothermal Stokes equations is presented. Gradient-robustness means that arbitrary gradient fields in the momentum balance are well-balanced by the discrete pressure gradient --- if there is enough mass in the system to compensate the force. The scheme is asymptotic-preserving in the sense that it degenerates for low Mach numbers to a recent inf-sup stable and pressure-robust discretization for the incompressible Stokes equations. The convergence of the coupled FEM-FVM scheme for the nonlinear, isothermal Stokes equations is proved by compactness arguments. Numerical examples illustrate the numerical analysis, and show that the novel approach can lead to a dramatically increased accuracy in nearly-hydrostatic low Mach number flows. Numerical examples also suggest that a straight-forward extension to barotropic situations with nonlinear equations of state is feasible. -
I. Selmer, P. Farrell, I. Smirnova, P. Gurikov, Comparison of finite difference method and finite volume method simulations for a mass transport model describing the supercritical drying kinetic of gel particles in a packed bed, Gels, 6 (2020), pp. 45/1--45/26, DOI 10.3390/gels6040045 .
-
N. Ahmed, V. John, An assessment of two classes of variational multiscale methods for the simulation of incompressible turbulent flows, Computer Methods in Applied Mechanics and Engineering, 365 (2020), pp. 112997/1--112997/20, DOI 10.1016/j.cma.2020.112997 .
Abstract
A numerical assessment of two classes of variational multiscale (VMS) methods for the simulation of incompressible flows is presented. Two types of residual-based VMS methods and two types of projection-based VMS methods are included in this assessment. The numerical simulations are performed at turbulent channel flow problems with various friction Reynolds numbers. It turns out the the residual-based VMS methods, in particular when used with a pair of inf-sup stable finite elements, give usually the most accurate results for second order statistics. For this pair of finite element spaces, a flexible GMRES method with a Least Squares Commutator (LSC) preconditioner proved to be an efficient solver. -
B. García-Archilla, V. John, J. Novo, Symmetric pressure stabilization for equal-order finite element approximations to the time-dependent Navier--Stokes equations, IMA Journal of Numerical Analysis, 41 (2021), pp. 1093--1129 (published online on 23.06.2020), DOI 10.1093/imanum/draa037 .
-
D. Janke, A. Caiazzo, N. Ahmed, N. Alia, O. Knoth, B. Moreau, U. Wilbrandt, D. Willink, Th. Amon, V. John, On the feasibility of using open source solvers for the simulation of a turbulent air flow in a dairy barn, Computers and Electronics in Agriculture, 175 (2020), pp. 105546/1--105546/16, DOI 10.1016/j.compag.2020.105546 .
Abstract
Two transient open source solvers, OpenFOAM and ParMooN, are assessed with respect to the simulation of the turbulent air flow inside and around a dairy barn. For this purpose, data were obtained in an experimental campaign at a 1:100 scaled wind tunnel model. Both solvers used different meshes, discretization schemes, and turbulence models. The experimental data and numerical results agree well for time-averaged stream-wise and vertical-wise velocities. In particular, the air exchange was predicted with high accuracy by both solvers with relative errors less than 5 % compared to the experimental results. With respect to the turbulent quantities, good agreements at the second (downwind) half of the barn inside and especially outside the barn could be achieved, where both codes accurately predicted the flow separation and the root-mean-square velocities. Deviations between simulations and experimental results regarding turbulent quantities could be observed in the first part of the barn, due to different inlet conditions between the experimental setup and the numerical simulations. Both solvers proved to be promising tools for the accurate prediction of time-dependent phenomena in an agricultural context, e.g., like the transport of particulate matter or pathogen-laden aerosols in and around agricultural buildings. -
C.K. Macnamara, A. Caiazzo, I. Ramis-Conde, M.A.J. Chaplain, Computational modelling and simulation of cancer growth and migration within a 3D heterogeneous tissue: The effects of fibre and vascular structure, Journal of Computational Science, 40 (2020), pp. 101067/1--101067/24, DOI 10.1016/j.jocs.2019.101067 .
Abstract
The term cancer covers a multitude of bodily diseases, broadly categorised by having cells which do not behave normally. Since cancer cells can arise from any type of cell in the body, cancers can grow in or around any tissue or organ making the disease highly complex. Our research is focused on understanding the specific mechanisms that occur in the tumour microenvironment via mathematical and computational modeling. We present a 3D individual-based model which allows one to simulate the behaviour of, and spatio-temporal interactions between, cells, extracellular matrix fibres and blood vessels. Each agent (a single cell, for example) is fully realised within the model and interactions are primarily governed by mechanical forces between elements. However, as well as the mechanical interactions we also consider chemical interactions, for example, by coupling the code to a finite element solver to model the diffusion of oxygen from blood vessels to cells. The current state of the art of the model allows us to simulate tumour growth around an arbitrary blood-vessel network or along the striations of fibrous tissue. -
L. Blank, E. Meneses Rioseco, U. Wilbrandt, A. Caiazzo, Modeling, simulation, and optimization of geothermal energy production from hot sedimentary aquifers, Computer & Geosciences, 25 (2021), pp. 67--104 (published online on 02.09.2020), DOI 10.1007/s10596-020-09989-8 .
Abstract
Geothermal district heating development has been gaining momentum in Europe with numerous deep geothermal installations and projects currently under development. With the increasing density of geothermal wells, questions related to the optimal and sustainable reservoir exploitation become more and more important. A quantitative understanding of the complex thermo-hydraulic interaction between tightly deployed geothermal wells in heterogeneous temperature and permeability fields is key for a maximum sustainable use of geothermal resources. Motivated by the geological settings of the Upper Jurassic aquifer in the Greater Munich region, we develop a computational model based on finite element analysis and gradient-free optimization to simulate groundwater flow and heat transport in hot sedimentary aquifers, and investigate numerically the optimal positioning and spacing of multi-well systems. Based on our numerical simulations, net energy production from deep geothermal reservoirs in sedimentary basins by smart geothermal multi-well arrangements provides significant amounts of energy to meet heat demand in highly urbanized regions. Our results show that taking into account heterogeneous permeability structures and variable reservoir temperature may drastically affect the results in the optimal configuration. We demonstrate that the proposed numerical framework is able to efficiently handle generic geometrical and geologocal configurations, and can be thus flexibly used in the context of multi-variable optimization problems. Hence, this numerical framework can be used to assess the extractable geothermal energy from heterogeneous deep geothermal reservoirs by the optimized deployment of smart multi-well systems. -
D. Frerichs, Ch. Merdon, Divergence-preserving reconstructions on polygons and a really pressure-robust virtual element method for the Stokes problem, IMA Journal of Numerical Analysis, 42 (2022), pp. 597--619 (published online on 09.11.2020), DOI 10.1093/imanum/draa073 .
Abstract
Non divergence-free discretisations for the incompressible Stokes problem may suffer from a lack of pressure-robustness characterised by large discretisations errors due to irrotational forces in the momentum balance. This paper argues that also divergence-free virtual element methods (VEM) on polygonal meshes are not really pressure-robust as long as the right-hand side is not discretised in a careful manner. To be able to evaluate the right-hand side for the testfunctions, some explicit interpolation of the virtual testfunctions is needed that can be evaluated pointwise everywhere. The standard discretisation via an L2 -bestapproximation does not preserve the divergence and so destroys the orthogonality between divergence-free testfunctions and possibly eminent gradient forces in the right-hand side. To repair this orthogonality and restore pressure-robustness another divergence-preserving reconstruction is suggested based on Raviart--Thomas approximations on local subtriangulations of the polygons. All findings are proven theoretically and are demonstrated numerically in two dimensions. The construction is also interesting for hybrid high-order methods on polygonal or polyhedral meshes. -
V. John, P. Knobloch, P. Korsmeier, On the solvability of the nonlinear problems in an algebraically stabilized finite element method for evolutionary transport-dominated equations, Mathematics of Computation, 90 (2021), pp. 595--611 (published online on 16.11.2020), DOI 10.1090/mcom/3576 .
-
V. John, P. Knobloch, Existence of solutions of a finite element flux-corrected-transport scheme, Applied Mathematics Letters, 115 (2021), pp. 106932/1--106932/6 (published online on 01.12.2020), DOI 10.1016/j.aml.2020.106932 .
Abstract
The existence of a solution is proved for a nonlinear finite element flux-corrected-transport (FEM-FCT) scheme with arbitrary time steps for evolutionary convection-diffusion-reaction equations and transport equations. -
A. Linke, Ch. Merdon, M. Neilan, Pressure-robustness in quasi-optimal a priori estimates for the Stokes problem, Electronic Transactions on Numerical Analysis, 52 (2020), pp. 281--294, DOI 10.1553/etna_vol52s281 .
-
D. Peschka, S. Haefner, L. Marquant, K. Jacobs, A. Münch, B. Wagner, Signatures of slip in dewetting polymer films, Proceedings of the National Academy of Sciences of the United States of America, 116 (2019), pp. 9275--9284, DOI 10.1073/pnas.1820487116 .
-
N.R. Gauger, A. Linke, P. Schroeder, On high-order pressure-robust space discretisations, their advantages for incompressible high Reynolds number generalised Beltrami flows and beyond, SMAI Journal of Computational Mathematics, 5 (2019), pp. 89--129.
Abstract
Recently, high-order space discretisations were proposed for the numerical simulation of the incompressible Navier--Stokes equations at high Reynolds numbers, even for complicated domains from simulation practice. Although the overall spatial approximation order of the algorithms depends on the approximation quality of the boundary (often not better than third order), competitively accurate and efficient results were reported. In this contribution, first, a possible explanation for this somewhat surprising result is proposed: the velocity error of high-order space discretisations is more robust against quantitatively large and complicated pressure fields than low-order methods. Second, it is demonstrated that novel pressure-robust methods are significantly more accurate than comparable classical, non-pressure-robust space discretisations, whenever the quadratic, nonlinear convection term is a nontrivial gradient field like in certain generalised Beltrami flows at high Reynolds number. Then, pressure-robust methods even allow to halve the (formal) approximation order without compromising the accuracy. Third, classical high-order space discretisations are outperformed by pressure-robust methods whenever the boundary is not approximated with high-order accuracy. This improved accuracy of (low-order) pressure-robust mixed methods is explained in terms of a Helmholtz--Hodge projector, which cancels out the nonlinear convection term in any generalised Beltrami flow, since it is a gradient field. The numerical results are illustrated by a novel numerical analysis for pressure-robust and classical space discretisations. Further, the relevance of these results is discussed for flows that are not of Beltrami type. -
L. Heltai, A. Caiazzo, Multiscale modeling of vascularized tissues via non-matching immersed methods, International Journal of Numerical Methods in Biomedical Engineering, 35 (2019), pp. 3264/1--3264/32, DOI 10.1002/cnm.3264 .
Abstract
We consider a multiscale approach based on immersed methods for the efficient computational modeling of tissues composed of an elastic matrix (in two or three-dimensions) and a thin vascular structure (treated as a co-dimension two manifold) at a given pressure. We derive different variational formulations of the coupled problem, in which the effect of the vasculature can be surrogated in the elasticity equations via singular or hyper-singular forcing terms. These terms only depends on information defined on co-dimension two manifolds (such as vessel center line, cross sectional area, and mean pressure over cross section), thus drastically reducing the complexity of the computational model. We perform several numerical tests, ranging from simple cases with known exact solutions to the modeling of materials with random distributions of vessels. In the latter case, we use our immersed method to perform an in silico characterization of the mechanical properties of the effective biphasic material tissue via statistical simulations. -
A. Jha, V. John, A study of solvers for nonlinear AFC discretizations of convection-diffusion equations, Computational & Applied Mathematics, 78 (2019), pp. 3117--3138, DOI 10.1016/j.camwa.2019.04.020 .
-
P.L. Lederer, Ch. Merdon, J. Schöberl, Refined a posteriori error estimation for classical and pressure-robust Stokes finite element methods, Journal of Numerical Mathematics, 142 (2019), pp. 713--748.
Abstract
Recent works showed that pressure-robust modifications of mixed finite element methods for the Stokes equations outperform their standard versions in many cases. This is achieved by divergence-free reconstruction operators and results in pressure-independent velocity error estimates which are robust with respect to small viscosities. In this paper we develop a posteriori error control which reflects this robustness. -
L.O. Müller, A. Caiazzo, P.J. Blanco, Reduced-order unscented Kalman filter with observations in the frequency domain: Application to computational hemodynamics, IEEE Transactions on Biomedical Engineering, 66 (2019), pp. 1269--1276, DOI 10.1109/TBME.2018.2872323 .
Abstract
Objective: The aim of this work is to assess the potential of the reduced order unscented Kalman filter (ROUKF) in the context of computational hemodynamics, in order to estimate cardiovascular model parameters when employing real patient-specific data. Methods: The approach combines an efficient blood flow solver for one-dimensional networks (for the forward problem) with the parameter estimation problem cast in the frequency space. Namely, the ROUKF is used to correct model parameter after each cardiac cycle, depending on the discrepancies of model outputs with respect to available observations properly mapped into the frequency space. Results: First we validate the filter in frequency domain applying it in the context of a set of experimental measurements for an in vitro model. Second, we perform different numerical experiments aiming at parameter estimation using patient-specific data. Conclusion: Our results demonstrate that the filter in frequency domain allows a faster and more robust parameter estimation, when compared to its time domain counterpart. Moreover, the proposed approach allows to estimate parameters that are not directly related to the network but are crucial for targeting inter-individual parameter variability (e.g., parameters that characterize the cardiac output). Significance: The ROUKF in frequency domain provides a robust and flexible tool for estimating parameters related to cardiovascular mathematical models using in vivo data. -
P.W. Schroeder, V. John, P.L. Lederer, Ch. Lehrenfeld, G. Lube, J. Schöberl, On reference solutions and the sensitivity of the 2D Kelvin--Helmholtz instability problem, Computers & Mathematics with Applications. An International Journal, 77 (2019), pp. 1010--1028, DOI 10.1016/j.camwa.2018.10.030 .
-
J. DE Frutos, B. Garc'ia-Archilla, V. John, J. Novo, Error analysis of non inf-sup stable discretizations of the time-dependent Navier--Stokes equations with local projection stabilization, IMA Journal of Numerical Analysis, 39 (2019), pp. 1747--1786, DOI 10.1093/imanum/dry044 .
-
C. Bartsch, V. John, R.I.A. Patterson, Simulations of an ASA flow crystallizer with a coupled stochastic-deterministic approach, Comput. Chem. Engng., 124 (2019), pp. 350--363, DOI 10.1016/j.compchemeng.2019.01.012 .
Abstract
A coupled solver for population balance systems is presented, where the flow, temperature, and concentration equations are solved with finite element methods, and the particle size distribution is simulated with a stochastic simulation algorithm, a so-called kinetic Monte-Carlo method. This novel approach is applied for the simulation of an axisymmetric model of a tubular flow crystallizer. The numerical results are compared with experimental data. -
J. Fuhrmann, C. Guhlke, Ch. Merdon, A. Linke, R. Müller, Induced charge electroosmotic flow with finite ion size and solvation effects, Electrochimica Acta, 317 (2019), pp. 778--785, DOI 10.1016/j.electacta.2019.05.051 .
-
A. Linke, L.G. Rebholz, Pressure-induced locking in mixed methods for time-dependent (Navier--)Stokes equations, Journal of Computational Physics, 388 (2019), pp. 350--356, DOI 10.1016/j.jcp.2019.03.010 .
Abstract
We consider inf-sup stable mixed methods for the time-dependent incompressible Stokes and Navier--Stokes equations, extending earlier work on the steady (Navier-)Stokes Problem. A locking phenomenon is identified for classical inf-sup stable methods like the Taylor-Hood or the Crouzeix-Raviart elements by a novel, elegant and simple numerical analysis and corresponding numerical experiments, whenever the momentum balance is dominated by forces of a gradient type. More precisely, a reduction of the L2 convergence order for high order methods, and even a complete stall of the L2 convergence order for lowest-order methods on preasymptotic meshes is predicted by the analysis and practically observed. On the other hand, it is also shown that (structure-preserving) pressure-robust mixed methods do not suffer from this locking phenomenon, even if they are of lowest-order. A connection to well-balanced schemes for (vectorial) hyperbolic conservation laws like the shallow water or the compressible Euler equations is made. -
N. Alia, V. John, S. Ollila, Re-visiting the single-phase flow model for liquid steel ladle stirred by gas, Applied Mathematical Modelling. Simulation and Computation for Engineering and Environmental Systems. Elsevier Science Inc., New York, NY. English, English abstracts., 67 (2019), pp. 549--556 (published online on 21.11.2018), DOI 10.1016/j.apm.2018.11.005 .
-
M. Akbas, A. Linke, L.G. Rebholz, P.W. Schroeder, The analogue of grad-div stabilization in DG methods for incompressible flows: Limiting behavior and extension to tensor-product meshes, Computer Methods in Applied Mechanics and Engineering, 341 (2018), pp. 917--938, DOI 10.1016/j.cma.2018.07.019 .
Abstract
Grad-div stabilization is a classical remedy in conforming mixed finite element methods for incompressible flow problems, for mitigating velocity errors that are sometimes called poor mass conservation. Such errors arise due to the relaxation of the divergence constraint in classical mixed methods, and are excited whenever the spacial discretization has to deal with comparably large and complicated pressures. In this contribution, an analogue of grad-div stabilization is presented for nonconforming flow discretizations of Discontinuous Galerkin or nonconforming finite element type. Here the key is the penalization of the jumps of the normal velocities over facets of the triangulation, which controls the measure-valued part of the distributional divergence of the discrete velocity solution. Furthermore, we characterize the limit for arbitrarily large penalization parameters, which shows that the proposed nonconforming Discontinuous Galerkin methods remain robust and accurate in this limit. Several numerical examples illustrate the theory and show their relevance for the simulation of practical, nontrivial flows. -
G.R. Barrenechea, V. John, P. Knobloch, R. Rankin, A unified analysis of algebraic flux correction schemes for convection-diffusion equations, SeMA Journal. Boletin de la Sociedad Espannola de Matematica Aplicada, 75 (2018), pp. 655--685, DOI 10.1007/s40324-018-0160-6 .
-
C. Bertoglio, A. Caiazzo, Y. Bazilevs, M. Braack, M. Esmaily-Moghadam, V. Gravemeier, A.L. Marsden, O. Pironneau, I.E. Vignon-Clementel, W.A. Wall, Benchmark problems for numerical treatment of backflow at open boundaries, International Journal of Numerical Methods in Biomedical Engineering, 34 (2018), pp. e2918/1--e2918/34, DOI 10.1002/cnm.2918 .
Abstract
In computational fluid dynamics, incoming velocity at open boundaries, or backflow, often yields to unphysical instabilities already for moderate Reynolds numbers. Several treatments to overcome these backflow instabilities have been proposed in the literature. However, these approaches have not yet been compared in detail in terms of accuracy in different physiological regimes, in particular due to the difficulty to generate stable reference solutions apart from analytical forms. In this work, we present a set of benchmark problems in order to compare different methods in different backflow regimes (with a full reversal flow and with propagating vortices after a stenosis). The examples are implemented in FreeFem++ and the source code is openly available, making them a solid basis for future method developments. -
P.W. Schroeder, Ch. Lehrenfeld, A. Linke, G. Lube, Towards computable flows and robust estimates for inf-sup stable FEM applied to the time-dependent incompressible Navier--Stokes equations, SeMA Journal. Boletin de la Sociedad Espannola de Matematica Aplicada, 75 (2018), pp. 629--653, DOI 10.1007/s40324-018-0157-1 .
Abstract
Inf-sup stable FEM applied to time-dependent incompressible Navier--Stokes flows are considered. The focus lies on robust estimates for the kinetic and dissipation energies in a twofold sense. Firstly, pressure-robustness ensures the fulfilment of a fundamental invariance principle and velocity error estimates are not corrupted by the pressure approximability. Secondly, Re-semi-robustness means that constants appearing on the right-hand side of kinetic and dissipation energy error estimates (including Gronwall constants) do not explicitly depend on the Reynolds number. Such estimates rely on an essential regularity assumption for the gradient of the velocity, which is discussed in detail. In the sense of best practice, we review and establish pressure- and Re-semi-robust estimates for pointwise divergence-free H1-conforming FEM (like Scott--Vogelius pairs or certain isogeometric based FEM) and pointwise divergence-free H(div)-conforming discontinuous Galerkin FEM. For convection-dominated problems, the latter naturally includes an upwind stabilisation for the velocity which is not gradient-based. -
J. DE Frutos, B. Garc'ia-Archilla, V. John, J. Novo, Analysis of the grad-div stabilization for the time-dependent Navier--Stokes equations with inf-sup stable finite elements, Advances in Computational Mathematics, 44 (2018), pp. 195--225.
-
L. Blank, A. Caiazzo, F. Chouly, A. Lozinski, J. Mura, Analysis of a stabilized penalty-free Nitsche method for the Brinkman, Stokes, and Darcy problems, ESAIM: Mathematical Modelling and Numerical Analysis, 52 (2018), pp. 2149--2185, DOI 10.1051/m2an/2018063 .
-
N. Ahmed, C. Bartsch, V. John, U. Wilbrandt, An assessment of solvers for some saddle point problems emerging from the incompressible Navier--Stokes equations, Computer Methods in Applied Mechanics and Engineering, 331 (2018), pp. 492--513, DOI 10.1016/j.cma.2017.12.004 .
Abstract
Efficient incompressible flow simulations, using inf-sup stable pairs of finite element spaces, require the application of efficient solvers for the arising linear saddle point problems. This paper presents an assessment of different solvers: the sparse direct solver UMFPACK, the flexible GMRES (FGMRES) method with different coupled multigrid preconditioners, and FGMRES with Least Squares Commutator (LSC) preconditioners. The assessment is performed for steady-state and time-dependent flows around cylinders in 2d and 3d. Several pairs of inf-sup stable finite element spaces with second order velocity and first order pressure are used. It turns out that for the steady-state problems often FGMRES with an appropriate multigrid preconditioner was the most efficient method on finer grids. For the time-dependent problems, FGMRES with LSC preconditioners that use an inexact iterative solution of the velocity subproblem worked best for smaller time steps. -
N. Ahmed, V. John, G. Matthies, J. Novo, A local projection stabilization/continuous Galerkin--Petrov method for incompressible flow problems, Applied Mathematics and Computation, 333 (2018), pp. 304--324, DOI 10.1016/j.amc.2018.03.088 .
Abstract
The local projection stabilization (LPS) method in space is consid-ered to approximate the evolutionary Oseen equations. Optimal error bounds independent of the viscosity parameter are obtained in the continuous-in-time case for the approximations of both velocity and pressure. In addition, the fully discrete case in combination with higher order continuous Galerkin--Petrov (cGP) methods is studied. Error estimates of order k + 1 are proved, where k denotes the polynomial degree in time, assuming that the convective term is time-independent. Numerical results show that the predicted order is also achieved in the general case of time-dependent convective terms. -
N. Ahmed, A. Linke, Ch. Merdon, On really locking-free mixed finite element methods for the transient incompressible Stokes equations, SIAM Journal on Numerical Analysis, 56 (2018), pp. 185--209.
Abstract
Inf-sup stable mixed methods for the steady incompressible Stokes equations that relax the divergence constraint are often claimed to deliver locking-free discretizations. However, this relaxation leads to a pressure-dependent contribution in the velocity error, which is proportional to the inverse of the viscosity, thus giving rise to a (different) locking phenomenon. However, a recently proposed modification of the right hand side alone leads to a discretization that is really locking-free, i.e., its velocity error converges with optimal order and is independent of the pressure and the smallness of the viscosity. In this contribution, we extend this approach to the transient incompressible Stokes equations, where besides the right hand side also the velocity time derivative requires an improved space discretization. Semi-discrete and fully-discrete a-priori velocity and pressure error estimates are derived, which show beautiful robustness properties. Two numerical examples illustrate the superior accuracy of pressure-robust space discretizations in the case of small viscosities. -
M. Hintermüller, M. Hinze, Ch. Kahle, T. Keil, A goal-oriented dual-weighted adaptive finite element approach for the optimal control of a nonsmooth Cahn--Hilliard--Navier--Stokes system, Optimization and Engineering. International Multidisciplinary Journal to Promote Optimization Theory & Applications in Engineering Sciences, 19 (2018), pp. 629--662, DOI 10.1007/s11081-018-9393-6 .
Abstract
This paper is concerned with the development and implementation of an adaptive solution algorithm for the optimal control of a time-discrete Cahn--Hilliard--Navier--Stokes system with variable densities. The free energy density associated to the Cahn--Hilliard system incorporates the double-obstacle potential which yields an optimal control problem for a family of coupled systems in each time instant of a variational inequality of fourth order and the Navier--Stokes equation. A dual-weighed residual approach for goal-oriented adaptive finite elements is presented which is based on the concept of C-stationarity. The overall error representation depends on primal residual weighted by approximate dual quantities and vice versa as well as various complementary mismatch errors. Details on the numerical realization of the adaptive concept and a report on numerical tests are given. -
V. John, S. Kaya, J. Novo, Finite element error analysis of a mantle convection model, International Journal of Numerical Analysis and Modeling. Wuhan University, Wuhan and Institute for Scientific Computing and Information(ISCI), Edmonton, Alberta. English., 15 (2018), pp. 677--698, DOI 10.20347/WIAS.PREPRINT.2403 .
Abstract
A mantle convection model consisting of the stationary Stokes equations and a time-dependent convection-diffusion equation for the temperature is studied. The Stokes problem is discretized with a conforming inf-sup stable pair of finite element spaces and the temperature equation is stabilized with the SUPG method. Finite element error estimates are derived which show the dependency of the error of the solution of one problem on the error of the solution of the other equation. The dependency of the error bounds on the coefficients of the problem is monitored. -
V. John, P. Knobloch, J. Novo, Finite elements for scalar convection-dominated equations and incompressible flow problems -- A never ending story?, Computing and Visualization in Science, 19 (2018), pp. 47--63.
Abstract
The contents of this paper is twofold. First, important recent results concerning finite element methods for convection-dominated problems and incompressible flow problems are described that illustrate the activities in these topics. Second, a number of, in our opinion, important problems in these fields are discussed. -
A. Linke, Ch. Merdon, M. Neilan, F. Neumann, Quasi-optimality of a pressure-robust nonconforming finite element method for the Stokes problem, Mathematics of Computation, 87 (2018), pp. 1543--1566, DOI 10.1090/mcom/3344 .
Abstract
Nearly all classical inf-sup stable mixed finite element methods for the incompressible Stokes equations are not pressure-robust, i.e., the velocity error is dependent on the pressure. However, recent results show that pressure-robustness can be recovered by a non-standard discretization of the right hand side alone. This variational crime introduces a consistency error in the method which can be estimated in a straightforward manner provided that the exact velocity solution is sufficiently smooth. The purpose of this paper is to analyze the pressure-robust scheme with low regularity. The numerical analysis applies divergence-free H¹-conforming Stokes finite element methods as a theoretical tool. As an example, pressure-robust velocity and pressure a-priori error estimates will be presented for the (first order) nonconforming Crouzeix--Raviart element. A key feature in the analysis is the dependence of the errors on the Helmholtz projector of the right hand side data, and not on the entire data term. Numerical examples illustrate the theoretical results. -
P. Farrell, A. Linke, Uniform second order convergence of a complete flux scheme on unstructured 1D grids for a singularly perturbed advection-diffusion equation and some multidimensional extensions, Journal of Scientific Computing, 72 (2017), pp. 373--395, DOI 10.1007/s10915-017-0361-7 .
Abstract
The accurate and efficient discretization of singularly perturbed advection-diffusion equations on arbitrary 2D and 3D domains remains an open problem. An interesting approach to tackle this problem is the complete flux scheme (CFS) proposed by G. D. Thiart and further investigated by J. ten Thije Boonkkamp. For the CFS, uniform second order convergence has been proven on structured grids. We extend a version of the CFS to unstructured grids for a steady singularly perturbed advection-diffusion equation. By construction, the novel finite volume scheme is nodally exact in 1D for piecewise constant source terms. This property allows to use elegant continuous arguments in order to prove uniform second order convergence on unstructured one-dimensional grids. Numerical results verify the predicted bounds and suggest that by aligning the finite volume grid along the velocity field uniform second order convergence can be obtained in higher space dimensions as well. -
A. Linke, M. Neilan, L.G. Rebholz, N. Wilson, A connection between coupled and penalty projection timestepping schemes with FE spatial discretization for the Navier--Stokes equations, Journal of Numerical Mathematics, 25 (2017), pp. 229--248, DOI 10.1515/jnma-2016-1024 .
Abstract
We prove that in finite element settings where the divergence-free subspace of the velocity space has optimal approximation properties, the solution of Chorin/Temam projection methods for Navier-Stokes equations equipped with grad-div stabilization with parameter gamma, converge to the associated coupled method solution with rate 1/gamma as gamma goes to infinity. We prove this first for backward Euler schemes, and then extend the results to BDF2 schemes, and finally to schemes with outflow boundary conditions. Several numerical experiments are given which verify the convergence rate, and show how using projection methods in this setting with large grad-div stabilization parameters can dramatically improve accuracy. -
U. Wilbrandt, C. Bartsch, N. Ahmed, N. Alia, F. Anker, L. Blank, A. Caiazzo, S. Ganesan, S. Giere, G. Matthies, R. Meesala, A. Shamim, J. Venkatensan, V. John, ParMooN -- A modernized program package based on mapped finite elements, Computers & Mathematics with Applications. An International Journal, 74 (2017), pp. 74--88, DOI 10.1016/j.camwa.2016.12.020 .
-
S. Giere, V. John, Towards physically admissible reduced-order solutions for convection-diffusion problems, Applied Mathematics Letters, 73 (2017), pp. 78--83, DOI 10.1016/j.aml.2017.03.022 .
-
H. Antil, M. Hintermüller, R.H. Nochetto, Th.M. Surowiec, D. Wegner, Finite horizon model predictive control of electrowetting on dielectric with pinning, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 19 (2017), pp. 1--30, DOI 10.4171/IFB/375 .
-
J. Bulling, V. John, P. Knobloch, Isogeometric analysis for flows around a cylinder, Applied Mathematics Letters, 63 (2017), pp. 65--70.
-
P.L. Lederer, A. Linke, Ch. Merdon, J. Schöberl, Divergence-free reconstruction operators for pressure-robust Stokes discretizations with continuous pressure finite elements, SIAM Journal on Numerical Analysis, 55 (2017), pp. 1291--1314.
Abstract
Classical inf-sup stable mixed finite elements for the incompressible (Navier--)Stokes equations are not pressure-robust, i.e., their velocity errors depend on the continuous pressure. How-ever, a modification only in the right hand side of a Stokes discretization is able to reestablish pressure-robustness, as shown recently for several inf-sup stable Stokes elements with discontinuous discrete pressures. In this contribution, this idea is extended to low and high order Taylor--Hood and mini elements, which have continuous discrete pressures. For the modification of the right hand side a velocity reconstruction operator is constructed that maps discretely divergence-free test functions to exactly divergence-free ones. The reconstruction is based on local H(div)-conforming flux equilibration on vertex patches, and fulfills certain orthogonality properties to provide consistency and optimal a-priori error estimates. Numerical examples for the incompressible Stokes and Navier--Stokes equations confirm that the new pressure-robust Taylor--Hood and mini elements converge with optimal order and outperform signi--cantly the classical versions of those elements when the continuous pressure is comparably large. -
N. Ahmed, S. Becher, G. Matthies, Higher-order discontinuous Galerkin time stepping and local projection stabilization techniques for the transient Stokes problem, Computer Methods in Applied Mechanics and Engineering, 313 (2017), pp. 28--52.
Abstract
We introduce and analyze discontinuous Galerkin time discretizations coupled with continuous finite element methods based on equal-order interpolation in space for velocity and pressure in transient Stokes problems. Spatial stability of the pressure is ensured by adding a stabilization term based on local projection. We present error estimates for the semi-discrete problem after discretization in space only and for the fully discrete problem. The fully discrete pressure shows an instability in the limit of small time step length. Numerical tests are presented which confirm our theoretical results including the pressure instability. -
N. Ahmed, T.Ch. Rebollo, V. John, S. Rubino, A review of variational multiscale methods for the simulation of turbulent incompressible flows, Archives of Computational Methods in Engineering. State of the Art Reviews, 24 (2017), pp. 115--164.
Abstract
Various realizations of variational multiscale (VMS) methods for simulating turbulent incompressible flows have been proposed in the past fifteen years. All of these realizations obey the basic principles of VMS methods: They are based on the variational formulation of the incompressible Navier--Stokes equations and the scale separation is defined by projections. However, apart from these common basic features, the various VMS methods look quite different. In this review, the derivation of the different VMS methods is presented in some detail and their relation among each other and also to other discretizations is discussed. Another emphasis consists in giving an overview about known results from the numerical analysis of the VMS methods. A few results are presented in detail to highlight the used mathematical tools. Furthermore, the literature presenting numerical studies with the VMS methods is surveyed and the obtained results are summarized. -
N. Ahmed, T.Ch. Rebollo, V. John, S. Rubino, Analysis of a full space-time discretization of the Navier--Stokes equations by a local projection stabilization method, IMA Journal of Numerical Analysis, 37 (2017), pp. 1437--1467, DOI 10.1093/imanum/drw048 .
Abstract
A finite element error analysis of a local projection stabilization (LPS) method for the time-dependent Navier--Stokes equations is presented. The focus is on the high-order term-by-term stabilization method that has one level, in the sense that it is defined on a single mesh, and in which the projection-stabilized structure of standard LPS methods is replaced by an interpolation-stabilized structure. The main contribution is on proving, theoretically and numerically, the optimal convergence order of the arising fully discrete scheme. In addition, the asymptotic energy balance is obtained for slightly smooth flows. Numerical studies support the analytical results and illustrate the potential of the method for the simulation of turbulent flows. Smooth unsteady flows are simulated with optimal order of accuracy. -
N. Ahmed, A. Linke, Ch. Merdon, Towards pressure-robust mixed methods for the incompressible Navier--Stokes equations, Computational Methods in Applied Mathematics, 18 (2018), pp. 353--372 (published online on 18.11.2017), DOI 10.1515/cmam-2017-0047 .
Abstract
In this contribution, classical mixed methods for the incompressible Navier-Stokes equations that relax the divergence constraint and are discretely inf-sup stable, are reviewed. Though the relaxation of the divergence constraint was claimed to be harmless since the beginning of the 1970ies, Poisson locking is just replaced by another more subtle kind of locking phenomenon, which is sometimes called poor mass conservation. Indeed, divergence-free mixed methods and classical mixed methods behave qualitatively in a different way: divergence-free mixed methods are pressure-robust, which means that, e.g., their velocity error is independent of the continuous pressure. The lack of pressure-robustness in classical mixed methods can be traced back to a consistency error of an appropriately defined discrete Helmholtz projector. Numerical analysis and numerical examples reveal that really locking-free mixed methods must be discretely inf-sup stable and pressure-robust, simultaneously. Further, a recent discovery shows that locking-free, pressure-robust mixed methods do not have to be divergence-free. Indeed, relaxing the divergence constraint in the velocity trial functions is harmless, if the relaxation of the divergence constraint in some velocity test functions is repaired, accordingly. -
N. Ahmed, On the grad-div stabilization for the steady Oseen and Navier--Stokes equations, Calcolo. A Quarterly on Numerical Analysis and Theory of Computation, 54 (2017), pp. 471--501, DOI 10.1007/s10092-016-0194-z .
Abstract
This paper studies the parameter choice in the grad-div stabilization applied to the generalized problems of Oseen type. Stabilization parameters based on minimizing the H1(Ω) error of the velocity are derived which do not depend on the viscosity parameter. For the proposed parameter choices, the H1(Ω) error of the velocity is derived that shows a direct dependence on the viscosity parameter. Differences and common features to the situation for the Stokes equations are discussed. Numerical studies are presented which confirm the theoretical results. Moreover, for the Navier- Stokes equations, numerical simulations were performed on a two-dimensional ow past a circular cylinder. It turns out, for the MINI element, that the best results can be obtained without grad-div stabilization. -
V. John, A. Linke, Ch. Merdon, M. Neilan, L.G. Rebholz, On the divergence constraint in mixed finite element methods for incompressible flows, SIAM Review, 59 (2017), pp. 492--544, DOI 10.1137/15M1047696 .
Abstract
The divergence constraint of the incompressible Navier--Stokes equations is revisited in the mixed finite element framework. While many stable and convergent mixed elements have been developed throughout the past four decades, most classical methods relax the divergence constraint and only enforce the condition discretely. As a result, these methods introduce a pressure-dependent consistency error which can potentially pollute the computed velocity. These methods are not robust in the sense that a contribution from the right-hand side, which influences only the pressure in the continuous equations, impacts both velocity and pressure in the discrete equations. This paper reviews the theory and practical implications of relaxing the divergence constraint. Several approaches for improving the discrete mass balance or even for computing divergence-free solutions will be discussed: grad-div stabilization, higher order mixed methods derived on the basis of an exact de Rham complex, $bH(mathrmdiv)$-conforming finite elements, and mixed methods with an appropriate reconstruction of the test functions. Numerical examples illustrate both the potential effects of using non-robust discretizations and the improvements obtained by utilizing pressure-robust discretizations. -
A. Linke, Ch. Merdon, W. Wollner, Optimal L2 velocity error estimate for a modified pressure-robust Crouzeix--Raviart Stokes element, IMA Journal of Numerical Analysis, 37 (2017), pp. 354--374, DOI 10.1093/imanum/drw019 .
Abstract
Recently, a novel approach for the robust discretization of the incompressible Stokes equations was proposed that slightly modifies the nonconforming Crouzeix--Raviart element such that its velocity error becomes pressure-independent. The modification results in an O(h) consistency error that allows straightforward proofs for the optimal convergence of the discrete energy norm of the velocity and of the L2 norm of the pressure. However, though the optimal convergence of the velocity in the L2 norm was observed numerically, it appeared to be nontrivial to prove. In this contribution, this gap is closed. Moreover, the dependence of the error estimates on the discrete inf-sup constant is traced in detail, which shows that classical error estimates are extremely pessimistic on domains with large aspect ratios. Numerical experiments in 2D and 3D illustrate the theoretical findings. -
N. Rotundo, T.-Y. Kim, W. Jiang, L. Heltai, E. Fried, Error estimates of B-spline based finite-element method for the wind-driven ocean circulation, Journal of Scientific Computing, 69 (2016), pp. 430--459.
Abstract
We present the error analysis of a B-spline based finite-element approximation of the stream-function formulation of the large scale wind-driven ocean circulation. In particular, we derive optimal error estimates for h-refinement using a Nitsche-type variational formulations of the two simplied linear models of the stationary quasigeostrophic equations, namely the Stommel and Stommel--Munk models. Numerical results on rectangular and embedded geometries confirm the error analysis. -
A. Linke, G. Matthies, L. Tobiska, Robust arbitrary order mixed finite element methods for the incompressible Stokes equations with pressure independent velocity errors, ESAIM: Mathematical Modelling and Numerical Analysis, 50 (2016), pp. 289--309.
Abstract
Standard mixed finite element methods for the incompressible Navier-Stokes equations that relax the divergence constraint are not robust against large irrotational forces in the momentum balance and the velocity error depends on the continuous pressure. This robustness issue can be completely cured by using divergence-free mixed finite elements which deliver pressure-independent velocity error estimates. However, the construction of H1-conforming, divergence-free mixed finite element methods is rather difficult. Instead, we present a novel approach for the construction of arbitrary order mixed finite element methods which deliver pressure-independent velocity errors. The approach does not change the trial functions but replaces discretely divergence-free test functions in some operators of the weak formulation by divergence-free ones. This modification is applied to inf-sup stable conforming and nonconforming mixed finite element methods of arbitrary order in two and three dimensions. Optimal estimates for the incompressible Stokes equations are proved for the H1 and L2 errors of the velocity and the L2 error of the pressure. Moreover, both velocity errors are pressure-independent, demonstrating the improved robustness. Several numerical examples illustrate the results. -
C. Bertoglio, A. Caiazzo, A Stokes-residual backflow stabilization method applied to physiological flows, Journal of Computational Physics, 313 (2016), pp. 260--278.
Abstract
In computational fluid dynamics incoming flow at open boundaries, or emphbackflow, often yields to unphysical instabilities for high Reynolds numbers. It is widely accepted that this is due to the incoming energy arising from the convection term, which cannot be empha priori controlled when the velocity field is unknown at the boundary. In order to improve the robustness of the numerical simulations, we propose a stabilized formulation based on a penalization of the residual of a weak Stokes problem on the open boundary, whose viscous part controls the incoming convective energy, while the inertial term contributes to the kinetic energy. We also present different strategies for the approximation of the boundary pressure gradient, which is needed for defining the stabilization term. The method has the advantage that it does not require neither artificial modifications or extensions of the computational domain. Moreover, it is consistent with the Womersley solution. We illustrate our approach on numerical examples - both academic and real-life - relevant to blood and respiratory flows. The results also show that the stabilization parameter can be reduced with the mesh size. -
P. Bringmann, C. Carstensen, Ch. Merdon, Guaranteed error control for the pseudostress approximation of the Stokes equations, Numerical Methods for Partial Differential Equations. An International Journal, 32 (2016), pp. 1411--1432.
Abstract
The pseudostress approximation of the Stokes equations rewrites the stationary Stokes equations with pure (but possibly inhomogeneous) Dirichlet boundary conditions as another (equivalent) mixed scheme based on a stress in H(div) and the velocity in $L^2$. Any standard mixed finite element function space can be utilized for this mixed formulation, e.g. the Raviart-Thomas discretization which is related to the Crouzeix-Raviart nonconforming finite element scheme in the lowest-order case. The effective and guaranteed a posteriori error control for this nonconforming velocity-oriented discretization can be generalized to the error control of some piecewise quadratic velocity approximation that is related to the discrete pseudostress. The analysis allows for local inf-sup constants which can be chosen in a global partition to improve the estimation. Numerical examples provide strong evidence for an effective and guaranteed error control with very small overestimation factors even for domains with large anisotropy. -
A. Ern, D. Di Pietro, A. Linke, F. Schieweck, A discontinuous skeletal method for the viscosity-dependent Stokes problem, Computer Methods in Applied Mechanics and Engineering, 306 (2016), pp. 175--195.
Abstract
We devise and analyze arbitrary-order nonconforming methods for the discretization of the viscosity-dependent Stokes equations on simplicial meshes. We keep track explicitly of the viscosity and aim at pressure-robust schemes that can deal with the practically relevant case of body forces with large curl-free part in a way that the discrete velocity error is not spoiled by large pressures. The method is inspired from the recent Hybrid High-Order (HHO) methods for linear elasticity. After elimination of the auxiliary variables by static condensation, the linear system to be solved involves only discrete face-based velocities, which are polynomials of degree k >=0, and cell-wise constant pressures. Our main result is a pressure-independent energy-error estimate on the velocity of order (k+1). The main ingredient to achieve pressure-independence is the use of a divergence-preserving velocity reconstruction operator in the discretization of the body forces. We also prove an L2-pressure estimate of order (k+1) and an L2-velocity estimate of order (k+2), the latter under elliptic regularity. The local mass and momentum conservation properties of the discretization are also established. Finally, two- and three-dimensional numerical results are presented to support the analysis. -
M. Khodayari, P. Reinsberg, A.A. Abd-El-Latif, Ch. Merdon, J. Fuhrmann, H. Baltruschat, Determining solubility and diffusivity by using a flow cell coupled to a mass spectrometer, ChemPhysChem, 17 (2016), pp. 1647--1655.
-
J. DE Frutos, B. Garc'ia-Archilla, V. John, J. Novo, Grad-div stabilization for the evolutionary Oseen problem with inf-sup stable finite elements, Journal of Scientific Computing, 66 (2016), pp. 991--1024.
Abstract
The approximation of the time-dependent Oseen problem using inf-sup stable mixed finite elements in a Galerkin method with grad-div stabilization is studied. The main goal is to prove that adding a grad-div stabilization term to the Galerkin approximation has a stabilizing effect for small viscosity. Both the continuous-in-time and the fully discrete case (backward Euler method, the two-step BDF, and Crank--Nicolson schemes) are analyzed. In fact, error bounds are obtained that do not depend on the inverse of the viscosity in the case where the solution is sufficiently smooth. The bounds for the divergence of the velocity as well as for the pressure are optimal. The analysis is based on the use of a specific Stokes projection. Numerical studies support the analytical results. -
J. DE Frutos, V. John, J. Novo, Projection methods for incompressible flow problems with WENO finite difference schemes, Journal of Computational Physics, 309 (2016), pp. 368--386.
Abstract
Weighted essentially non-oscillatory (WENO) finite difference schemes have been recommended in a competitive study of discretizations for scalar evolutionary convection-diffusion equations [20]. This paper explores the applicability of these schemes for the simulation of incompressible flows. To this end, WENO schemes are used in several non-incremental and incremental projection methods for the incompressible Navier-Stokes equations. Velocity and pressure are discretized on the same grid. A pressure stabilization Petrov-Galerkin (PSPG) type of stabilization is introduced in the incremental schemes to account for the violation of the discrete inf-sup condition. Algorithmic aspects of the proposed schemes are discussed. The schemes are studied on several examples with different features. It is shown that the WENO finite difference idea can be transferred to the simulation of incompressible flows. Some shortcomings of the methods, which are due to the splitting in projection schemes, become also obvious. -
J. Fuhrmann, A. Linke, Ch. Merdon, F. Neumann, T. Streckenbach, H. Baltruschat, M. Khodayari, Inverse modeling of thin layer flow cells for detection of solubility, transport and reaction coefficients from experimental data, Electrochimica Acta, 211 (2016), pp. 1--10.
Abstract
Thin layer flow cells are used in electrochemical research as experimental devices which allow to perform investigations of electrocatalytic surface reactions under controlled conditions using reasonably small electrolyte volumes. The paper introduces a general approach to simulate the complete cell using accurate numerical simulation of the coupled flow, transport and reaction processes in a flow cell. The approach is based on a mass conservative coupling of a divergence-free finite element method for fluid flow and a stable finite volume method for mass transport. It allows to perform stable and efficient forward simulations that comply with the physical bounds namely mass conservation and maximum principles for the involved species. In this context, several recent approaches to obtain divergence-free velocities from finite element simulations are discussed. In order to perform parameter identification, the forward simulation method is coupled to standard optimization tools. After an assessment of the inverse modeling approach using known realistic data, first results of the identification of solubility and transport data for O2 dissolved in organic electrolytes are presented. A plausibility study for a more complex situation with surface reactions concludes the paper and shows possible extensions of the scope of the presented numerical tools. -
V. John, K. Kaiser, J. Novo, Finite element methods for the incompressible Stokes equations with variable viscosity, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 96 (2016), pp. 205--216.
Abstract
Finite element error estimates are derived for the incompressible Stokes equations with variable viscosity. The ratio of the supremum and the infimum of the viscosity appears in the error bounds. Numerical studies show that this ratio can be observed sometimes. However, often the numerical results show a weaker dependency on the viscosity. -
A. Linke, Ch. Merdon, On velocity errors due to irrotational forces in the Navier--Stokes momentum balance, Journal of Computational Physics, 313 (2016), pp. 654--661.
Abstract
This contribution studies the influence of the pressure on the velocity error in finite element discretisations of the Navier--Stokes equations. Three simple benchmark problems that are all close to real-world applications convey that the pressure can be comparably large and is not to be underestimated. For widely used finite element methods like the Taylor--Hood finite element method, such relatively large pressures can lead to spurious oscillations and arbitrarily large errors in the velocity, even if the exact velocity is in the ansatz space. Only mixed finite element methods, whose velocity error is pressure-independent, like the Scott--Vogelius finite element method can avoid this influence. -
A. Linke, Ch. Merdon, Pressure-robustness and discrete Helmholtz projectors in mixed finite element methods for the incompressible Navier--Stokes equations, Computer Methods in Applied Mechanics and Engineering, 311 (2016), pp. 304--326.
Abstract
Recently, it was understood how to repair a certain L2-orthogonality of discretely-divergence-free vector fields and gradient fields such that the velocity error of inf-sup stable discretizations for the incompressible Stokes equations becomes pressure-independent. These new 'pressure-robust' Stokes discretizations deliver a small velocity error, whenever the continuous velocity field can be well approximated on a given grid. On the contrary, classical inf-sup stable Stokes discretizations can guarantee a small velocity error only, when both the velocity and the pressure field can be approximated well, simultaneously.
In this contribution, 'pressure-robustness' is extended to the time-dependent Navier--Stokes equations. In particular, steady and time-dependent potential flows are shown to build an entire class of benchmarks, where pressure-robust discretizations can outperform classical approaches significantly. Speedups will be explained by a new theoretical concept, the 'discrete Helmholtz projector' of an inf-sup stable discretization. Moreover, different discrete nonlinear convection terms are discussed, and skew-symmetric pressure-robust discretizations are proposed. -
G.R. Barrenechea, V. John, P. Knobloch, Some analytical results for an algebraic flux correction scheme for a steady convection-diffusion equation in one dimension, IMA Journal of Numerical Analysis, 34 (2015), pp. 1729--1756.
Abstract
Algebraic flux correction schemes are nonlinear discretizations of convection dominated problems. In this work, a scheme from this class is studied for a steady-state convection--diffusion equation in one dimension. It is proved that this scheme satisfies the discrete maximum principle. Also, as it is a nonlinear scheme, the solvability of the linear subproblems arising in a Picard iteration is studied, where positive and negative results are proved. Furthermore, the non-existence of solutions for the nonlinear scheme is proved by means of counterexamples. Therefore, a modification of the method, which ensures the existence of a solution, is proposed. A weak version of the discrete maximum principle is proved for this modified method. -
CH. Brennecke, A. Linke, Ch. Merdon, J. Schöberl, Optimal and pressure-independent $L^2$ velocity error estimates for a modified Crouzeix--Raviart Stokes element with BDM reconstructions, Journal of Computational Mathematics, 33 (2015), pp. 191--208.
Abstract
Nearly all inf-sup stable mixed finite elements for the incompressible Stokes equations relax the divergence constraint. The price to pay is that a priori estimates for the velocity error become pressure-dependent, while divergence-free mixed finite elements deliver pressure-independent estimates. A recently introduced new variational crime using lowest-order Raviart-Thomas velocity reconstructions delivers a much more robust modified Crouzeix-Raviart element, obeying an optimal pressure-independent discrete H1 velocity estimate. Refining this approach, a more sophisticated variational crime employing the lowest-order BDM element is proposed, which also allows proving an optimal pressure independent L2 velocity error. Numerical examples confirm the analysis and demonstrate the improved robustness in the Navier-Stokes case. -
V. John, J. Novo, Analysis of the pressure stabilized Petrov--Galerkin (PSPG) method stabilization for the evolutionary Stokes equations avoiding time-step restrictions, SIAM Journal on Numerical Analysis, 53 (2015), pp. 1005--1031.
Abstract
Optimal error estimates for the pressure stabilized Petrov--Galerkin (PSPG) method for the continuous-in-time discretization of the evolutionary Stokes equations are proved in the case of regular solutions. The main result is applicable to higher order finite elements. The error bounds for the pressure depend on the error of the pressure at the initial time. An approach is suggested for choosing the discrete initial velocity in such a way that this error is bounded. The “instability of the discrete pressure for small time steps”, which is reported in the literature, is discussed on the basis of the analytical results. Numerical studies confirm the theoretical results, showing in particular that this instability does not occur for the proposed initial condition. -
S. Giere, T. Iliescu, V. John, D. Wells, SUPG reduced order models for convection-dominated convection-diffusion-reaction equations, Computer Methods in Applied Mechanics and Engineering, 289 (2015), pp. 454--474.
Abstract
This paper presents a Streamline-Upwind Petrov--Galerkin (SUPG) reduced order model (ROM) based on Proper Orthogonal Decomposition (POD). This ROM is investigated theoretically and numerically for convection-dominated convection-diffusion-reaction equations. The SUPG finite element method was used on realistic meshes for computing the snapshots, leading to some noise in the POD data. Numerical analysis is used to propose the scaling of the stabilization parameter for the SUPG-ROM. Two approaches are used: One based on the underlying finite element discretization and the other one based on the POD truncation. The resulting SUPG-ROMs and the standard Galerkin ROM (G-ROM) are studied numerically. For many settings, the results obtained with the SUPG-ROMs are more accurate. Finally, one of the choices for the stabilization parameter is recommended. -
A. Caiazzo, R. Guibert, Y. Boudjemline, I.E. Vignon-Clementel, Efficient blood flow simulations for the design of stented valve reducer in enlarged ventricular outflow tracts, Cardiovascular Engineering and Technology, 6 (2015), pp. 485--500.
Abstract
Tetralogy of Fallot is a congenital heart disease characterized over time, after the initial repair, by the absence of a functioning pulmonary valve, which causes regurgitation, and by progressive enlargement of the right ventricle and pulmonary arteries. Due to this pathological anatomy, available transcatheter valves are usually too small to be deployed in the enlarged right ventricular outflow tracts (RVOT). To avoid surgical valve replacement, an alternative consists in implanting a reducer prior to or in combination with a transcatheter valve. We describe a computational model to study the effect of a stented valve RVOT reducer on the hemodynamics in enlarged ventricular outflow tracts. To this aim, blood flow in the right ventricular outflow tract is modeled via the incompressible Navier--Stokes equations coupled to a simplified valve model, numerically solved with a standard finite element method and with a reduced order model based on Proper Orthogonal Decomposition (POD). Numerical simulations are based on a patient geometry obtained from medical imaging and boundary conditions tuned according to measurements of inlet flow rates and pressures. Different geometrical models of the reducer are built, varying its length and/or diameter, and compared with the initial device-free state. Simulations thus investigate multiple device configurations and describe the effect of geometry on hemodynamics. Forces exerted on the valve and on the reducer are monitored, varying with geometrical parameters. Results support the thesis that the reducer does not introduce significant pressure gradients, as was found in animal experiments. Finally, we demonstrate how computational complexity can be reduced with POD. -
A. Caiazzo, G. Montecinos, L.O. Müller, E.M. Haacke, E.F. Toro, Computational haemodynamics in stenotic internal jugular veins, Journal of Mathematical Biology, 70 (2015), pp. 745--772.
Abstract
Stenosis in internal jugular veins (IJVs) are frequently associated to pathological venous circulation and insufficient cerebral blood drainage. In this work, we set up a computational framework to assess the relevance of IJV stenoses through numerical simulation, combining medical imaging, patient-specific data and a mathematical model for venous occlusions. Coupling a three-dimensional (3D) description of blood flow in IJVs with a reduced one-dimesional model (1D) for major intracranial veins, we are able to model different anatomical configurations, an aspect of importance to understand the impact of IJV stenosis in intracranial venous haemodynamics. We investigate several stenotic configurations in a physiologic patient-specific regime, quantifying the effect of the stenosis in terms of venous pressure increase and wall shear stress patterns. Simulation results are in qualitative agreement with reported pressure anomalies in pathological cases. Moreover, they demonstrate the potential of the proposed multiscale framework for individual-based studies and computer-aided diagnosis. -
A. Caiazzo, I. Ramis-Conde, Multiscale modeling of palisade formation in glioblastoma multiforme, Journal of Theoretical Biology, 383 (2015), pp. 145--156.
Abstract
Palisades are characteristic tissue aberrations that arise in glioblastomas. Observation of palisades is considered as a clinical indicator of the transition from a noninvasive to an invasive tumour. In this article we propose a computational model to study the influence of genotypic and phenotypic heterogeneity in palisade formation. For this we produced three dimensional realistic simulations, based on a multiscale hybrid model, coupling the evolution of tumour cells and the oxygen diffusion in tissue, that depict the shape of palisades during its formation. Our results can be summarized as the following: (1) we show that cell heterogeneity is a crucial factor in palisade formation and tumour growth; (2) we present results that can explain the observed fact that recursive tumours are more malignant than primary tumours; and (3) the presented simulations can provide to clinicians and biologists for a better understanding of palisades 3D structure as well as glioblastomas growth dynamics -
A. Linke, Ch. Merdon, Guaranteed energy error estimators for a modified robust Crouzeix--Raviart Stokes element, Journal of Scientific Computing, 64 (2015), pp. 541--558.
Abstract
This paper provides guaranteed upper energy error bounds for a modified lowest-order nonconforming Crouzeix--Raviart finite element method for the Stokes equations. The modification from [A. Linke 2014, On the role of the Helmholtz-decomposition in mixed methods for incompressible flows and a new variational crime] is based on the observation that only the divergence-free part of the right-hand side should balance the vector Laplacian. The new method has optimal energy error estimates and can lead to errors that are smaller by several magnitudes, since the estimates are pressure-independent. An efficient a posteriori velocity error estimator for the modified method also should involve only the divergence-free part of the right-hand side. Some designs to approximate the Helmholtz projector are compared and verified by numerical benchmark examples. They show that guaranteed error control for the modified method is possible and almost as sharp as for the unmodified method. -
A. Linke, On the role of the Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime, Computer Methods in Applied Mechanics and Engineering, 268 (2014), pp. 782--800.
Abstract
According to the Helmholtz decomposition, the irrotational parts of the momentum balance equations of the incompressible Navier-Stokes equations are balanced by the pressure gradient. Unfortunately, nearly all mixed methods for incompressible flows violate this fundamental property, resulting in the well-known numerical instability of poor mass conservation. The origin of this problem is the lack of L2-orthogonality between discretely divergence-free velocities and irrotational vector fields. In order to cure this, a new variational crime using divergence-free velocity reconstructions is proposed. Applying lowest order Raviart-Thomas velocity reconstructions to the nonconforming Crouzeix-Raviart element allows to construct a cheap flow discretization for general 2d and 3d simplex meshes that possesses the same advantageous robustness properties like divergence-free flow solvers. In the Stokes case, optimal a-priori error estimates for the velocity gradients and the pressure are derived. Moreover, the discrete velocity is independent of the continuous pressure. Several detailed linear and nonlinear numerical examples illustrate the theoretical findings. -
E. Jenkins, V. John, A. Linke, L.G. Rebholz, On the parameter choice in grad-div stabilization for the Stokes equations, Advances in Computational Mathematics, 40 (2014), pp. 491--516.
Abstract
Grad-div stabilization has been proved to be a very useful tool in discretizations of incompressible flow problems. Standard error analysis for inf-sup stable conforming pairs of finite element spaces predicts that the stabilization parameter should be optimally chosen to be O(1). This paper revisits this choice for the Stokes equations on the basis of minimizing the $H^1$ error of the velocity and the $L^2$ error of the pressure. It turns out, by applying a refined error analysis, that the optimal parameter choice is more subtle than known so far in the literature. It depends on the used norm, the solution, the family of finite element spaces, and the type of mesh. Depending on the situation, the optimal stabilization parameter might range from being very small to very large. The analytic results are supported by numerical examples. -
C. Bertoglio, A. Caiazzo, A tangential regularization method for backflow stabilization in hemodynamics, Journal of Computational Physics, 261 (2014), pp. 162--171.
Abstract
In computational simulations of fluid flows, instabilities at the Neumann boundaries may appear during backflow regime. It is widely accepted that this is due to the incoming energy at the boundary, coming from the convection term, which cannot be controlled when the velocity field is unknown. We propose a stabilized formulation based on a local regularization of the fluid velocity along the tangential directions on the Neumann boundaries. The stabilization term is proportional to the amount of backflow, and does not require any further assumption on the velocity profile. The perfomance of the method is assessed on a two- and three-dimensional Womersley flows, as well as considering a hemodynamic physiological regime in a patient-specific aortic geometry. -
R. Eymard, J. Fuhrmann, A. Linke, On MAC schemes on triangular Delaunay meshes, their convergence and application to coupled flow problems, Numerical Methods for Partial Differential Equations. An International Journal, 30 (2014), pp. 1397--1424.
Abstract
We study two classical generalized MAC schemes on unstructured triangular Delaunay meshes for the incompressible Stokes and Navier-Stokes equations and prove their convergence for the first time. These generalizations use the duality between Voronoi and triangles of Delaunay meshes, in order to construct two staggered discretization schemes. Both schemes are especially interesting, since compatible finite volume discretizations for coupled convection-diffusion equations can be constructed which preserve discrete maximum principles. In the first scheme, called tangential velocity scheme, the pressures are defined at the vertices of the mesh, and the discrete velocities are tangential to the edges of the triangles. In the second scheme, called normal velocity scheme, the pressures are defined in the triangles, and the discrete velocities are normal to the edges of the triangles. For both schemes, we prove the convergence in $L^2$ for the velocities and the discrete rotations of the velocities for the Stokes and the Navier-Stokes problem. Further, for the normal velocity scheme, we also prove the strong convergence of the pressure in $L^2$. Linear and nonlinear numerical examples illustrate the theoretical predictions. -
J. DE Frutos, B. Garc'ia-Archilla, V. John, J. Novo, An adaptive SUPG method for evolutionary convection-diffusion equations, Computer Methods in Applied Mechanics and Engineering, 273 (2014), pp. 219--237.
Abstract
An adaptive algorithm for the numerical simulation of time-dependent convection-diffusion-reaction equations will be proposed and studied. The algorithm allows the use of the natural extension of any error estimator for the steady-state problem for controlling local refinement and coarsening. The main idea consists in considering the SUPG solution of the evolutionary problem as the SUPG solution of a particular steady-state convection-diffusion problem with data depending on the computed solution. The application of the error estimator is based on a heuristic argument by considering a certain term to be of higher order. This argument is supported in the one-dimensional case by numerical analysis. In the numerical studies, particularly the residual-based error estimator from [18] will be applied, which has proved to be robust in the SUPG norm. The effectivity of this error estimator will be studied and the numerical results (accuracy of the solution, fineness of the meshes) will be compared with results obtained by utilizing the adaptive algorithm proposed in [6]. -
A. Caiazzo, T. Iliescu, V. John, S. Schyschlowa, A numerical investigation of velocity-pressure reduced order models for incompressible flows, Journal of Computational Physics, 259 (2014), pp. 598--616.
Abstract
This report has two main goals. First, it numerically investigates three velocity-pressure reduced order models (ROMs) for incompressible flows. The proper orthogonal decomposition (POD) is used to generate the modes. One method computes the ROM pressure solely based on the velocity POD modes, whereas the other two ROMs use pressure modes as well. To the best of the authors' knowledge, one of the latter methods is novel. The second goal is to numerically investigate the impact of the snapshot accuracy on the ROMs accuracy. Numerical studies are performed on a two-dimensional laminar flow past a circular obstacle. It turns out that, both in terms of accuracy and efficiency, the two ROMs that utilize pressure modes are clearly superior to the ROM that uses only velocity modes. The numerical results also show a strong correlation of the accuracy of the snap shots with the accuracy of the ROMs. -
A. Caiazzo, V. John, U. Wilbrandt, On classical iterative subdomain methods for the Stokes--Darcy problem, Computer & Geosciences, 18 (2014), pp. 711--728.
Abstract
Iterative subdomain methods for the Stokes--Darcy problem that use Robin boundary conditions on the interface are reviewed. Their common underlying structure and their main differences are identified. In particular, it is clarified that there are different updating strategies for the interface conditions. For small values of fluid viscosity and hydraulic permeability, which are relevant in applications from geosciences, it is shown in numerical studies that only one of these updating strategies leads to an efficient numerical method, if this strategy is used in combination with appropriate parameters in the Robin boundary conditions. In particular, it is observed that the values of appropriate parameters are larger than those proposed so far. Not only the size but also the ratio of appropriate Robin parameters depends on the coefficients of the problem. -
V. John, L. Schumacher, A study of isogeometric analysis for scalar convection-diffusion equations, Applied Mathematics Letters, 27 (2014), pp. 43--48.
-
R. Bordás, V. John, E. Schmeyer, D. Thévenin, Numerical methods for the simulation of a coalescence-driven droplet size distribution, Theoretical and Computational Fluid Dynamics. Springer-Verlag, Berlin., 27 (2013), pp. 253--271.
Abstract
A droplet size distribution in a turbulent flow field is considered and modeled by means of a population balance system. This paper studies different numerical methods for the 4D population balance equation and their impact on an output of interest, the time-space-averaged droplet size distribution at the outlet which is known from experiments. These methods include different interpolations of the experimental data at the inlet, various discretizations in time and space, and different schemes for computing the aggregation integrals. It will be shown that notable changes in the output of interest might occur. In addition, the efficiency of the studied methods is discussed. -
G.R. Barrenechea, V. John, P. Knobloch, A local projection stabilization finite element method with nonlinear crosswind diffusion for convection-diffusion-reaction equations, ESAIM: Mathematical Modelling and Numerical Analysis, 47 (2013), pp. 1335--1366.
Abstract
An extension of the local projection stabilization (LPS) finite element method for convection-diffusion-reaction equations is presented and analyzed, both in the steady-state and the transient setting. In addition to the standard LPS method, a nonlinear crosswind diffusion term is introduced that accounts for the reduction of spurious oscillations. The existence of a solution can be proved and, depending on the choice of the stabilization parameter, also its uniqueness. Error estimates are derived which are supported by numerical studies. These studies demonstrate also the reduction of the spurious oscillations. -
A. Bradji, J. Fuhrmann, Some abstract error estimates of a finite volume scheme for a nonstationary heat equation on general nonconforming multidimensional spatial meshes, Applications of Mathematics, 58 (2013), pp. 1--38.
Abstract
A general class of nonconforming meshes has been recently studied for stationary anisotropic heterogeneous diffusion problems by R. Eymard and coworkers. Thanks to these basic ideas developed for stationary problems, we derive a new discretization scheme in order to approximate the nonstationary heat problem. The unknowns of this scheme are the values at the centre of the control volumes, at some internal interfaces, and at the mesh points of the time discretization. Although the numerical scheme stems from the finite volume method, its formulation is based on the discrete version for the weak formulation defined for the heat problem. We derive error estimates for the solution in discrete norm, and an error estimate for an approximation of the gradient, in a general framework in which the discrete bilinear form is satisfying ellipticity. We prove in particular, that, when the discrete flux is calculated using a stabilized discrete gradient, the convergence order is h+k , where h (resp. k) is the mesh size of the spatial (resp. time) discretization. This estimate is valid under the regularity assumption that the exact solution is twice continuously differentiable in time and space. These error estimates are useful because they allow us to get error estimates for the approximations of the exact solution and its first derivatives. -
B. Cousins, S. Le Borne, A. Linke, Z. Wang, Efficient linear solvers for incompressible flow simulations using Scott--Vogelius finite elements, Numerical Methods for Partial Differential Equations. An International Journal, 29 (2013), pp. 1217--1237.
Abstract
Recent research has shown that in some practically relevant situations like multiphysics flows (Galvin et al., Comput Methods Appl Mech Eng, 2012) divergence-free mixed finite elements may have a significantly smaller discretization error than standard nondivergence-free mixed finite elements. To judge the overall performance of divergence-free mixed finite elements, we investigate linear solvers for the saddle point linear systems arising in Scott-Vogelius finite element implementations of the incompressible Navier-Stokes equations. We investigate both direct and iterative solver methods. Due to discontinuous pressure elements in the case of Scott-Vogelius (SV) elements, considerably more solver strategies seem to deliver promising results than in the case of standard mixed finite elements such as Taylor-Hood elements. For direct methods, we extend recent preliminary work using sparse banded solvers on the penalty method formulation to finer meshes and discuss extensions. For iterative methods, we test augmented Lagrangian and H -LU preconditioners with GMRES, on both full and statically condensed systems. Several numerical experiments are provided that show these classes of solvers are well suited for use with SV elements and could deliver an interesting overall performance in several applications. -
V. John, J. Novo, A robust SUPG norm a posteriori error estimator for stationary convection-diffusion equations, Computer Methods in Applied Mechanics and Engineering, 255 (2013), pp. 289--305.
Abstract
A robust residual-based a posteriori estimator is proposed for the SUPG finite element method applied to stationary convection-diffusion-reaction equations. The error in the natural SUPG norm is estimated. The main concern of this paper is the consideration of the convection-dominated regime. A global upper bound and a local lower bound for the error are derived, where the global upper estimate relies on some hypotheses. Numerical studies demonstrate the robustness of the estimator and the fulfillment of the hypotheses. A comparison to other residual-based estimators with respect to the adaptive grid refinement is also provided. -
A. Linke, L. Rebholz, On a reduced sparsity stabilization of grad-div type for incompressible flow problems, Computer Methods in Applied Mechanics and Engineering, 261--262 (2013), pp. 142--153.
Abstract
We introduce a new operator for stabilizing error that arises from the weak enforcement of mass conservation in finite element simulations of incompressible flow problems. We show this new operator has a similar positive effect on velocity error as the well-known and very successful grad-div stabilization operator, but the new operator is more attractive from an implementation standpoint because it yields a sparser block structure matrix. That is, while grad-div produces fully coupled block matrices (i.e. block-full), the matrices arising from the new operator are block-upper triangular in two dimensions, and in three dimensions the 2,1 and 3,1 blocks are empty. Moreover, the diagonal blocks of the new operator's matrices are identical to those of grad-div. We provide error estimates and numerical examples for finite element simulations with the new operator, which reveals the significant improvement in accuracy it can provide. Solutions found using the new operator are also compared to those using usual grad-div stabilization, and in all cases, solutions are found to be very similar. -
R. Bordás, V. John, E. Schmeyer, D. Thévenin, Measurement and simulation of a droplet population in a turbulent flow field, Computers and Fluids. Pergamon Press, Oxford., 66 (2012), pp. 52--62.
Abstract
The interaction of a disperse droplet population (spray) in a turbulent flow field is studied by combining wind tunnel experiments with simulations based on the model of a population balance system. The behavior of the droplets is modeled numerically by a population balance equation. Velocities of the air and of the droplets are determined by non-intrusive measurements. A direct discretization of the 4D equation for the droplet size distribution is used in the simulations. Important components of the numerical algorithm are a variational multiscale method for turbulence modeling, an upwind scheme for the 4D equation and a pre-processing approach to evaluate the aggretation integrals. The simulations of this system accurately predict the modifications of the droplet size distribution from the inlet to the outlet of the measurement section. Since the employed configuration is simple and considering that all measurement data are freely available thanks to an Internet-based repository, the considered experiment is proposed as a benchmark problem for the simulation of disperse two-phase turbulent flows. -
R. Eymard, Th. Gallouët, R. Herbin, A. Linke, Finite volume schemes for the biharmonic problem on general meshes, Mathematics of Computation, 81 (2012), pp. 2019--2048.
Abstract
We propose a finite volume scheme for the approximation of a biharmonic problem with Dirichlet boundary conditions. We prove that the piece-wise constant approximate solution converges to the exact solution, as well as the discrete approximate of the gradient and the discrete approximate of the Laplacian of the exact solution. These results are confirmed by numerical results. -
K. Galvin, A. Linke, L. Rebholz, N. Wilson, Stabilizing poor mass conservation in incompressible flow problems with large irrotational forcing and application to thermal convection, Computer Methods in Applied Mechanics and Engineering, 237--240 (2012), pp. 166--176.
Abstract
We consider the problem of poor mass conservation in mixed finite element algorithms for flow problems with large rotation-free forcing in the momentum equation. We provide analysis that suggests for such problems, obtaining accurate solutions necessitates either the use of pointwise divergence-free finite elements (such as Scott-Vogelius), or heavy grad-div stabilization of weakly divergence-free elements. The theory is demonstrated in numerical experiments for a benchmark natural convection problem, where large irrotational forcing occurs with high Rayleigh numbers. -
W. Hackbusch, V. John, A. Khachatryan, C. Suciu, A numerical method for the simulation of an aggregation-driven population balance system, International Journal for Numerical Methods in Fluids, 69 (2012), pp. 1646--1660.
Abstract
A population balance system which models the synthesis of urea is studied in this paper. The equations for the flow field, the mass and the energy balances are given in a three-dimensional domain and the equation for the particle size distribution (PSD) in a four-dimensional domain. This problem is convection-dominated and aggregation-driven. Both features require the application of appropriate numerical methods. This paper presents a numerical approach for simulating the population balance system which is based on finite element schemes, a finite difference method and a modern method to evaluate convolution integrals that appear in the aggregation term. Two experiments are considered and the numerical results are compared with experimental data. Unknown parameters in the aggregation kernel have to be calibrated. For appropriately chosen parameters, good agreements are achieved of the experimental data and the numerical results computed with the proposed method. A detailed study of the computational results reveals the influence of different parts of the aggregation kernel. -
M. Augustin, A. Caiazzo, A. Fiebach, J. Fuhrmann, V. John, A. Linke, R. Umla, An assessment of discretizations for convection-dominated convection-diffusion equations, Computer Methods in Applied Mechanics and Engineering, 200 (2011), pp. 3395--3409.
Abstract
The performance of several numerical schemes for discretizing convection-dominated convection-diffusion equations will be investigated with respect to accuracy and efficiency. Accuracy is considered in measures which are of interest in applications. The study includes an exponentially fitted finite volume scheme, the Streamline-Upwind Petrov--Galerkin (SUPG) finite element method, a spurious oscillations at layers diminishing (SOLD) finite element method, a finite element method with continuous interior penalty (CIP) stabilization, a discontinuous Galerkin (DG) finite element method, and a total variation diminishing finite element method (FEMTVD). A detailed assessment of the schemes based on the Hemker example will be presented. -
M. Case, V. Ervin, A. Linke, L. Rebholz, N. Wilson, Stable computing with an enhanced physics based scheme for the 3D Navier--Stokes equations, International Journal of Numerical Analysis and Modeling. Wuhan University, Wuhan and Institute for Scientific Computing and Information(ISCI), Edmonton, Alberta. English., 8 (2011), pp. 118--136.
Abstract
We study extensions of an earlier developed energy and helicity preserving scheme for the 3D Navier-Stokes equations and apply them to a more general class of problems. The scheme is studied together with stabilizations of grad-div type in order to mitigate the effect of the Bernoulli pressure error on the velocity error. We prove stability, convergence, discuss conservation properties, and present numerical experiments that demonstrate the advantages of the scheme. -
M. Case, V. Ervin, A. Linke, L. Rebholz, A connection between Scott--Vogelius and grad-div stabilized Taylor--Hood FE approximations of the Navier--Stokes equations, SIAM Journal on Numerical Analysis, 49 (2011), pp. 1461--1481.
Abstract
This article studies two methods for obtaining excellent mass conservation in finite element computations of the Navier-Stokes equations using continuous velocity fields. Under mild restrictions, the Scott-Vogelius element pair has recently been shown to be inf-sup stable and have optimal approximation properties, while also providing pointwise mass conservation. We present herein the first numerical tests of this element pair for the time dependent Navier-Stokes equations. We also prove that, again under these mild restrictions, the limit of the grad-div stabilized Taylor-Hood solutions to the Navier-Stokes problem converges to the Scott-Vogelius solution as the stabilization parameter tends to infinity. That is, in this setting, we provide theoretical justification that choosing the parameter large does not destroy the solution. A limiting result is also proven for the general case. Numerical tests are provided which verify the theory, and show how both Scott-Vogelius and grad-div stabilized Taylor-Hood (with large stabilization parameter) elements can provide accurate results with excellent mass conservation for Navier-Stokes approximations. -
A. Caiazzo, D. Evans, J.-L. Falcone, J. Hegewald, E. Lorenz, ET AL., A complex automata approach for in-stent restenosis: Two-dimensional multiscale modeling and simulations, Journal of Computational Science, 2 (2011), pp. 9--17.
-
J. Fuhrmann, H. Langmach, A. Linke, A numerical method for mass conservative coupling between fluid flow and solute transport, Applied Numerical Mathematics. An IMACS Journal, 61 (2011), pp. 530--553.
Abstract
We present a new coupled discretization approach for species transport in an incompressible fluid. The Navier-Stokes equations for the flow are discretized by the divergence-free Scott-Vogelius element on barycentrically refined meshes guaranteeing LBB stability. The convection-diffusion equation for species transport is discretized by the Voronoi finite volume method. In accordance to the continuous setting, due to the exact integration of the normal component of the flow through the Voronoi surfaces, the species concentration fulfills discrete global and local maximum principles. Besides of the the numerical scheme itself, we present important aspects of its implementation. Further, for the case of homogeneous Dirichlet boundary conditions, we give a convergence proof for the coupled scheme. We report results of the application of the scheme to the interpretation of limiting current measurements in an electrochemical flow cell with cylindrical shape. -
A.L. Bowers, B.R. Cousins, A. Linke, L.G. Rebholz, New connections between finite element formulations of the Navier--Stokes equations, Journal of Computational Physics, 229 (2010), pp. 9020--9025.
Abstract
We show the velocity solutions to the convective, skew-symmetric, and rotational Galerkin finite element formulations of the Navier-Stokes equations are identical if Scott-Vogelius elements are used, and thus all three formulations will the same pointwise divergence free solution velocity. A connection is then established between the formulations for grad-div stabilized Taylor-Hood elements: under mild restrictions, the formulations' velocity solutions converge to each other (and to the Scott-Vogelius solution) as the stabilization parameter tends to infinity. Thus the benefits of using Scott-Vogelius elements can be obtained with the less expensive Taylor-Hood elements, and moreover the benefits of all the formulations can be retained if the rotational formulation is used. Numerical examples are provided that confirm the theory. -
A. Glitzky, J.A. Griepentrog, Discrete Sobolev--Poincaré inequalities for Voronoi finite volume approximations, SIAM Journal on Numerical Analysis, 48 (2010), pp. 372--391.
Abstract
We prove a discrete Sobolev-Poincare inequality for functions with arbitrary boundary values on Voronoi finite volume meshes. We use Sobolev's integral representation and estimate weakly singular integrals in the context of finite volumes. We establish the result for star shaped polyhedral domains and generalize it to the finite union of overlapping star shaped domains. In the appendix we prove a discrete Poincare inequality for space dimensions greater or equal to two. -
V. John, A. Kindl, O.C. Suciu, Finite element LES and VMS methods on tetrahedral meshes, Journal of Computational and Applied Mathematics, (2010), pp. 3095--3102.
-
V. John, A. Kindl, A variational multiscale method for turbulent flow simulation with adaptive large scale space, Journal of Computational Physics, 229 (2010), pp. 301--312.
-
V. John, A. Kindl, Numerical studies of finite element variational multiscale methods for turbulent flow simulations, Computer Methods in Applied Mechanics and Engineering, 199 (2010), pp. 841--852.
-
V. John, J. Rang, Adaptive time step control for the incompressible Navier--Stokes equations, Computer Methods in Applied Mechanics and Engineering, 199 (2010), pp. 514--524.
-
V. John, M. Roland, On the impact of the scheme for solving the higher-dimensional equation in coupled population balance systems, International Journal for Numerical Methods in Engineering, 82 (2010), pp. 1450--1474.
-
S. Bartels, M. Jensen, R. Müller, Discontinuous Galerkin finite element convergence for incompressible miscible displacement problems of low regularity, SIAM Journal on Numerical Analysis, 47 (2009), pp. 3720--3743.
-
P. Rudolph, M. Czupalla, N. Dropka, Ch. Frank-Rotsch, F.-M. Kiessling, O. Klein, B. Lux, W. Miller, U. Rehse, O. Root, Crystal growth from melt in combined heater-magnet modules, Journal of the Korean Crystal Growth and Crystal Technology, 19 (2009), pp. 215-222.
-
A. Glitzky, Energy estimates for electro-reaction-diffusion systems with partly fast kinetics, Discrete and Continuous Dynamical Systems, 25 (2009), pp. 159--174.
Abstract
We start from a basic model for the transport of charged species in heterostructures containing the mechanisms diffusion, drift and reactions in the domain and at its boundary. Considering limit cases of partly fast kinetics we derive reduced models. This reduction can be interpreted as some kind of projection scheme for the weak formulation of the basic electro--reaction--diffusion system. We verify assertions concerning invariants and steady states and prove the monotone and exponential decay of the free energy along solutions to the reduced problem and to its fully implicit discrete-time version by means of the results of the basic problem. Moreover we make a comparison of prolongated quantities with the solutions to the basic model. -
A. Glitzky, K. Gärtner, Energy estimates for continuous and discretized electro-reaction-diffusion systems, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 70 (2009), pp. 788--805.
Abstract
We consider electro-reaction-diffusion systems consisting of continuity equations for a finite number of species coupled with a Poisson equation. We take into account heterostructures, anisotropic materials and rather general statistic relations.
We investigate thermodynamic equilibria and prove for solutions to the evolution system the monotone and exponential decay of the free energy to its equilibrium value. Here the essential idea is an estimate of the free energy by the dissipation rate which is proved indirectly.
The same properties are shown for an implicit time discretized version of the problem. Moreover, we provide a space discretized scheme for the electro-reaction-diffusion system which is dissipative (the free energy decays monotonously). On a fixed grid we use for each species different Voronoi boxes which are defined with respect to the anisotropy matrix occurring in the flux term of this species. -
V. John, T. Mitkova, M. Roland, K. Sundmacher, L. Tobiska, A. Voigt, Simulations of population balance systems with one internal coordinate using finite element methods, Chemical Engineering Sciences, 64 (2009), pp. 733--741.
-
O. Klein, Ch. Lechner, P.-É. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F.M. Kiessling, W. Miller, U. Rehse, P. Rudolph, Numerical simulations of the influence of a traveling magnetic field, generated by an internal heater-magnet module, on liquid encapsulated Czochralski crystal growth, Magnetohydrodynamics. Consultants Bureau, New York (US). Consultants Bureau, New York. Translation from: Magnitnaya Gidrodinamika., 45 (2009), pp. 557-567.
-
A. Glitzky, Exponential decay of the free energy for discretized electro-reaction-diffusion systems, Nonlinearity, 21 (2008), pp. 1989--2009.
Abstract
Our focus are electro-reaction-diffusion systems consisting of continuity equations for a finite number of species coupled with a Poisson equation. We take into account heterostructures, anisotropic materials and rather general statistical relations. We introduce a discretization scheme (in space and fully implicit in time) using a fixed grid but for each species different Voronoi boxes which are defined with respect to the anisotropy matrix occurring in the flux term of this species. This scheme has the special property that it preserves the main features of the continuous systems, namely positivity, dissipativity and flux conservation. For the discretized electro-reaction-diffusion system we investigate thermodynamic equilibria and prove for solutions to the evolution system the monotone and exponential decay of the free energy to its equilibrium value. The essential idea is an estimate of the free energy by the dissipation rate which is proved indirectly. -
O. Klein, Ch. Lechner, P.-É. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F.M. Kiessling, W. Miller, U. Rehse, P. Rudolph, Numerical simulation of Czochralski crystal growth under the influence of a traveling magnetic field generated by an internal heater-magnet module (HMM), Journal of Crystal Growth, 310 (2008), pp. 1523-1532.
-
H. Stephan, A. Khrabustovskyi, Positivity and time behavior of a linear reaction-diffusion system, non-local in space and time, Mathematical Methods in the Applied Sciences, 31 (2008), pp. 1809--1834.
Abstract
We consider a general linear reaction-diffusion system in three dimensions and time, containing diffusion (local interaction), jumps (nonlocal interaction) and memory effects. We prove a maximum principle, and positivity of the solution, and investigate its asymptotic behavior. Moreover, we give an explicite expression of the limit of the solution for large times. In order to obtain these results we use the following method: We construct a Riemannian manifold with complicated microstructure depending on a small parameter. We study the asymptotic behavior of the solution of a simple diffusion equation on this manifold as the small parameter tends to zero. It turns out that the homogenized system coincides with the original reaction-diffusion system what allows us to investigate its properties. -
CH. Lechner, O. Klein, P.-É. Druet, Development of a software for the numerical simulation of VCz growth under the influence of a traveling magnetic field, Journal of Crystal Growth, 303 (2007), pp. 161-164.
-
J. Geiser, O. Klein, P. Philip, Influence of anisotropic thermal conductivity in the apparatus insulation for sublimation growth of SiC: Numerical investigation of heat transfer, Crystal Growth & Design, 6 (2006), pp. 2021--2028.
-
J. Geiser, O. Klein, P. Philip, Transient numerical study of temperature gradients during sublimation growth of SiC: Dependence on apparatus design, Journal of Crystal Growth, 297 (2006), pp. 20-32.
-
O. Klein, F. Luterotti, R. Rossi, Existence and asymptotic analysis of a phase field model for supercooling, Quarterly of Applied Mathematics, 64 (2006), pp. 291-319.
-
P. Philip, O. Klein, Transient conductive-radiative heat transfer: Discrete existence and uniqueness for a finite volume scheme, Mathematical Models & Methods in Applied Sciences, 15 (2005), pp. 227--258.
-
A. Glitzky, R. Hünlich, Global existence result for pair diffusion models, SIAM Journal on Mathematical Analysis, 36 (2005), pp. 1200--1225.
-
A. Glitzky, R. Hünlich, Stationary energy models for semiconductor devices with incompletely ionized impurities, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 85 (2005), pp. 778--792.
-
J. Griepentrog, On the unique solvability of a nonlocal phase separation problem for multicomponent systems, Banach Center Publications, 66 (2004), pp. 153-164.
-
H. Gajewski, I.V. Skrypnik, On unique solvability of nonlocal drift-diffusion-type problems, Nonlinear Analysis. Theory, Methods & Applications. An International Multidisciplinary Journal. Series A: Theory and Methods, 56 (2004), pp. 803--830.
-
H. Gajewski, I.V. Skrypnik, To the uniqueness problem for nonlinear parabolic equations, Discrete and Continuous Dynamical Systems, 10 (2004), pp. 315--336.
-
A. Glitzky, R. Hünlich, Stationary solutions of two-dimensional heterogeneous energy models with multiple species, Banach Center Publications, 66 (2004), pp. 135-151.
-
A. Glitzky, Electro-reaction-diffusion systems with nonlocal constraints, Mathematische Nachrichten, 277 (2004), pp. 14--46.
-
O. Klein, Asymptotic behaviour for a phase-field model with hysteresis in one-dimensional thermo-visco-plasticity, Applications of Mathematics, 49 (2004), pp. 309--341.
-
H. Gajewski, K. Zacharias, On a nonlocal phase separation model, Journal of Mathematical Analysis and Applications, 286 (2003), pp. 11--31.
-
G. Albinus, H. Gajewski, R. Hünlich, Thermodynamic design of energy models of semiconductor devices, Nonlinearity, 15 (2002), pp. 367--383.
-
H. Gajewski, On a nonlocal model of non-isothermal phase separation, Advances in Mathematical Sciences and Applications, 12 (2002), pp. 569--586.
-
A. Glitzky, R. Hünlich, Global properties of pair diffusion models, Advances in Mathematical Sciences and Applications, 11 (2001), pp. 293--321.
-
A. Glitzky, R. Hünlich, Electro-reaction-diffusion systems including cluster reactions of higher order, Mathematische Nachrichten, 216 (2000), pp. 95--118.
-
J.A. Griepentrog, An application of the Implicit Function Theorem to an energy model of the semiconductor theory, ZAMM. Zeitschrift für Angewandte Mathematik und Mechanik, 79 (1999), pp. 43--51.
Abstract
In this paper we deal with a mathematical model for the description of heat conduction and carrier transport in semiconductor heterostructures. We solve a coupled system of nonlinear elliptic differential equations consisting of the heat equation with Joule heating as a source, the Poisson equation for the electric field an drift-diffusion equations with temperature dependent coefficients describing the charge and current conservation, subject to general thermal and electrical boundary conditions. We prove the existence and uniqueness of Holder continuous weak solutions near thermodynamic equilibria points using the Implicit Function Theorem. To show the differentiability of maps corresponding to the weak formulation of the problem we use regularity results from the theory of nonsmooth linear elliptic boundary value problems in Sobolev-Campanato spaces.
 Contributions to Collected Editions
Contributions to Collected Editions
-
D. Frerichs-Mihov, M. Zainelabdeen, V. John, On collocation points for physics-informed neural networks applied to convection-dominated convection-diffusion problems, in: Numerical Mathematics and Advanced Applications ENUMATH 2023, Volume 1, A. Sequeira, A. Silvestre, S.S. Valtchev, J. Janela, eds., 153 of Lecture Notes in Computational Science and Engineering (LNCSE), Springer, Cham, 2025, pp. 335--344, DOI 10.1007/978-3-031-86173-4_34 .
Abstract
In recent years physics-informed neural networks (PINNs) for approximating the solution to (initial-)boundary value problems gained a lot of interest. PINNs are trained to minimize several residuals of the problem in collocation points. In this work we tackle convection-dominated convection-diffusion problems, whose solutions usually possess layers, which are small regions where the solution has a steep gradient. Inspired by classical Shishkin meshes, we compare hard- constrained PINNs trained with layer-adapted collocation points with ones trained with equispaced and uniformly randomly chosen points. We observe that layer-adapted points work the best for a problem with an interior layer and the worst for a problem with boundary layers. For both problems at most acceptable solutions can be obtained with PINNs. -
A. Linke, Ch. Merdon, On the significance of pressure-robustness for the space discretization of incompressible high Reynolds number flows, in: Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, R. Klöfkorn, E. Keilegavlen, A.F. Radu, J. Fuhrmann, eds., 323 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, pp. 103--112.
-
A. Linke, Ch. Merdon, Well-balanced discretisation for the compressible Stokes problem by gradient-robustness, in: Finite Volumes for Complex Applications IX -- Methods, Theoretical Aspects, Examples -- FVCA 9, Bergen, June 2020, R. Klöfkorn, E. Keilegavlen, A.F. Radu, J. Fuhrmann, eds., 323 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2020, pp. 113--121.
-
A. Jha, V. John, On basic iteration schemes for nonlinear AFC discretizations, in: Boundary and Interior Layers, Computational and Asymptotic Methods, BAIL 2018, G.N. Barrenechea, J. Mackenzie, eds., 135 of Lecture Notes in Computational Science and Engineering, Springer, Cham, 2020, pp. 113--128, DOI https://doi.org/10.1007/978-3-030-41800-7_7 .
Abstract
Algebraic flux correction (AFC) finite element discretizations of steady-state convection-diffusion-reaction equations lead to a nonlinear problem. This paper presents first steps of a systematic study of solvers for these problems. Two basic fixed point iterations and a formal Newton method are considered. It turns out that the fixed point iterations behave often quite differently. Using a sparse direct solver for the linear problems, one of them exploits the fact that only one matrix factorization is needed to become very efficient in the case of convergence. For the behavior of the formal Newton method, a clear picture is not yet obtained. -
J. Fuhrmann, C. Guhlke, A. Linke, Ch. Merdon, R. Müller, Models and numerical methods for electrolyte flows, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 183--209.
-
J. Fuhrmann, C. Guhlke, A. Linke, Ch. Merdon, R. Müller, Voronoi finite volumes and pressure robust finite elements for electrolyte models with finite ion sizes, in: Numerical Geometry, Grid Generation and Scientific Computing. Proceedings of the 9th International Conference, NUMGRID 2018 / Voronoi 150, V.A. Garanzha, L. Kamenski, H. Si, eds., 131 of Lecture Notes in Computational Science and Engineering, Springer Nature Switzerland AG, Cham, 2019, pp. 73--83, DOI 10.1007/978-3-030-23436-2 .
-
N. Ahmed, A. Linke, Ch. Merdon, Towards pressure-robust mixed methods for the incompressible Navier--Stokes equations, in: Finite Volumes for Complex Applications VIII -- Methods and Theoretical Aspects, FVCA 8, Lille, France, June 2017, C. Cancès, P. Omnes, eds., 199 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing AG, Cham, 2017, pp. 351--359.
-
P. Farrell, A. Linke, Uniform second order convergence of a complete flux scheme on nonuniform 1D grids, in: Finite Volumes for Complex Applications VIII -- Methods and Theoretical Aspects, FVCA 8, Lille, France, June 2017, C. Cancès, P. Omnes, eds., 199 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing AG, Cham, 2017, pp. 303--310.
-
S. Ganesan, V. John, G. Matthies, R. Meesala, A. Shamim, U. Wilbrandt, An object oriented parallel finite element scheme for computations of PDEs: Design and implementation, in: 2016 IEEE 23rd International Conference on High Performance Computing Workshops (PDF only), pp. 106--115, DOI 10.1109/HiPCW.2016.19 .
-
CH. Brennecke, A. Linke, Ch. Merdon, J. Schöberl, Optimal and pressure-independent $L^2$ velocity error estimates for a modified Crouzeix--Raviart element with BDM reconstructions, in: Finite Volumes for Complex Applications VII -- Methods and Theoretical Aspects -- FVCA 7, Berlin, June 2014, J. Fuhrmann, M. Ohlberger, Ch. Rohde, eds., 77 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2014, pp. 159--167.
Abstract
Nearly all inf-sup stable mixed finite elements for the incompressible Stokes equations relax the divergence constraint. The price to pay is that a priori estimates for the velocity error become pressure-dependent, while divergence-free mixed finite elements deliver pressure-independent estimates. A recently introduced new variational crime using lowest-order Raviart-Thomas velocity reconstructions delivers a much more robust modified Crouzeix-Raviart element, obeying an optimal pressure-independent discrete H1 velocity estimate. Refining this approach, a more sophisticated variational crime employing the lowest-order BDM element is proposed, which also allows proving an optimal pressureindependent L2 velocity error. Numerical examples confirm the analysis and demonstrate the improved robustness in the Navier-Stokes case. -
J. Fuhrmann, A. Linke, Ch. Merdon, Coupling of fluid flow and solute transport using a divergence-free reconstruction of the Crouzeix--Raviart element, in: Finite Volumes for Complex Applications VII -- Elliptic, Parabolic and Hyperbolic Problems -- FVCA 7, Berlin, June 2014, J. Fuhrmann, M. Ohlberger, Ch. Rohde, eds., 78 of Springer Proceedings in Mathematics & Statistics, Springer International Publishing, Cham et al., 2014, pp. 587--595.
-
A. Glitzky, J.A. Griepentrog, On discrete Sobolev--Poincaré inequalities for Voronoi finite volume approximations, in: Finite volumes for complex applications VI: Problems and perspectives, J. Fořt, J. Fürst, J. Halama, R. Herbin, F. Hubert, eds., Springer Proceedings in Mathematics 4, Springer, Heidelberg, 2011, pp. 533--541.
-
S. Bartels, R. Müller, Die kalte Zunge, in: Besser als Mathe --- Moderne angewandte Mathematik aus dem MATHEON zum Mitmachen, K. Biermann, M. Grötschel, B. Lutz-Westphal, eds., Reihe: Populär, Vieweg+Teubner, Wiesbaden, 2010, pp. 227--235.
-
M. Jensen, R. Müller, Stable Crank--Nicolson discretisation for incompressible miscible displacement problems of low regularity, in: Numerical Mathematics and Advanced Applications 2009, Part 2, G. Kreiss, P. Lötstedt, A. Målqvist, M. Neytcheva, eds., Springer, Heidelberg et al., pp. 469--477.
Abstract
In this article we study the numerical approximation of incompressible miscible displacement problems with a linearised Crank-Nicolson time discretisation, combined with a mixed finite element and discontinuous Galerkin method. At the heart of the analysis is the proof of convergence under low regularity requirements. Numerical experiments demonstrate that the proposed method exhibits second-order convergence for smooth and robustness for rough problems. -
V. John, E. Schmeyer, On finite element methods for 3D time-dependent convection-diffusion-reaction equations with small diffusion, in: BAIL 2008 --- Boundary and Interior Layers, A. Hegarty, N. Kopteva, E. O'Riordan, M. Stynes, eds., 69 of Lecture Notes in Computational Science and Engineering, Springer, Berlin/Heidelberg, 2009, pp. 173--181.
-
H. Gajewski, H.-Chr. Kaiser, H. Langmach, R. Nürnberg, R.H. Richter, Mathematical modelling and numerical simulation of semiconductor detectors, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 355--364.
-
R. Hünlich, G. Albinus, H. Gajewski, A. Glitzky, W. Röpke, J. Knopke, Modelling and simulation of power devices for high-voltage integrated circuits, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 401--412.
-
U. Bandelow, H. Gajewski, H.-Chr. Kaiser, Modeling combined effects of carrier injection, photon dynamics and heating in Strained Multi-Quantum-Well Laser, in: Physics and Simulation of Optoelectronic Devices VIII, R.H. Binder, P. Blood, M. Osinski, eds., 3944 of Proceedings of SPIE, SPIE, Bellingham, WA, 2000, pp. 301--310.
-
G. Schwarz, E. Schöll, R. Nürnberg, H. Gajewski, Simulation of current filamentation in an extended drift-diffusion model, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1334--1336.
-
H. Gajewski, K. Zacharias, On a reaction-diffusion system modelling chemotaxis, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1098--1103.
-
R. Hünlich, A. Glitzky, On energy estimates for electro-diffusion equations arising in semiconductor technology, in: Partial differential equations. Theory and numerical solution, W. Jäger, J. Nečas, O. John, K. Najzar, eds., 406 of Chapman & Hall Research Notes in Mathematics, Chapman & Hall, Boca Raton, FL, 2000, pp. 158--174.
-
H.-Chr. Kaiser, J. Rehberg, About some mathematical questions concerning the embedding of Schrödinger-Poisson systems into the drift-diffusion model of semiconductor devices, in: EQUADIFF 99: International Conference on Differential Equations, Berlin 1999, B. Fiedler, K. Gröger, J. Sprekels, eds., 2, World Scientific, Singapore [u. a.], 2000, pp. 1328--1333.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
O. Pártl, E. Meneses Rioseco, Computational framework for modeling, simulation, and optimization of geothermal energy production from naturally fractured reservoirs, Preprint no. 3239, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3239 .
Abstract, PDF (51 MByte)
We describe an open-source computational framework for the automated search for deviated multi-well lay- outs in hot fracture-controlled reservoirs that sustainably optimize geothermal energy production. This search is performed via 3D simulations of groundwater flow and heat transfer. We model the reservoirs as geologi- cally consistent, randomly generated discrete fracture networks (DFNs) in which the fractures are 2D manifolds with polygonal boundaries embedded in a 3D porous medium. The wells are modeled as line sources and sinks. The flow and heat transport in the DFN-matrix system are modeled by solving the balance equations for mass and energy, while expressing the momentum balance by the Darcy law. The spatial discretization is based on the finite element method stabilized via the algebraic flux correction. For the time discretization, we use a semi-implicit approach to enhance the solver efficiency. The optimization is performed via a gradient-free global optimization algorithm. By employing the immersed boundary method and a non-matching discretization strategy, the need for computationally expensive remeshing when altering well configurations within the reser- voir is effectively eliminated, thereby enhancing the robustness of the proposed framework and enabling fully automated optimization. We present the results of our optimization tests for randomly generated DFNs consist- ing of thousands of fractures, considering realistic values of physical parameters. To demonstrate the analytical capabilities of our open-source framework, we use it to analyze and visualize the above optimization results and the structure of the above DFNs. The developed framework was verified and validated using a set of simpli- fied yet purpose-specific fracture configurations relevant to geothermal energy extraction in naturally fractured reservoirs. -
A. Alphonse, A. Djurdjevac, E. Engström, E. Hansen, Transmission problems and domain decompositions for non--autonomous parabolic equations on evolving domains, Preprint no. 3187, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3187 .
Abstract, PDF (400 kByte)
Parabolic equations on evolving domains model a multitude of applications including various industrial processes such as the molding of heated materials. Such equations are numerically challenging as they require large-scale computations and the usage of parallel hardware. Domain decomposition is a common choice of numerical method for stationary domains, as it gives rise to parallel discretizations. In this study, we introduce a variational framework that extends the use of such methods to evolving domains. In particular, we prove that transmission problems on evolving domains are well posed and equivalent to the corresponding parabolic problems. This in turn implies that the standard non-overlapping domain decompositions, including the Robin-Robin method, become well defined approximations. Furthermore, we prove the convergence of the Robin-Robin method. The framework is based on a generalization of fractional Sobolev-Bochner spaces on evolving domains, time-dependent Steklov-Poincaré operators, and elements of the approximation theory for monotone maps. -
R. Araya, C. Cárcamo, A.H. Poza, A stabilized finite element method for the Navier--Stokes/Darcy coupled problem, Preprint no. 3183, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3183 .
Abstract, PDF (2163 kByte)
In this work, we propose, analyze, and numerically verify a new stabilized finite element method for the Navier--Stokes/Darcy coupled problem, which models a fluid flowing through a free medium into a porous medium. At the interface between both domains, we impose mass conservation, the balance of normal forces, and the well-known Beavers--Joseph--Saffman con- ditions [9]. The stabilization terms are defined using Galerkin's least-squares stabilization for the Navier--Stokes equation and Masud--Hughes stabilization [30] for the Darcy equation. This new discrete scheme employs equal-order elements to approximate the velocity and pressure of the fluid and generalizes the scheme recently analyzed for the linear case in [4]. The well-posedness of the discrete problem is established via fixed-point theorems under small data conditions, and we prove optimal error estimates in natural norms. Finally, we present numerical examples to confirm the expected theoretical convergence orders in cases where a manufactured solution is available, as well as to demonstrate the effectiveness of our scheme in a physical model with varying permeability fields. -
D. Peschka, M. Thomas, A. Zafferi, Reference map approach to Eulerian thermomechanics using GENERIC, Preprint no. 3178, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3178 .
Abstract, PDF (7829 kByte)
An Eulerian GENERIC model for thermo-viscoelastic materials with diffusive components is derived based on a transformation framework that maps a Lagrangian formulation to corresponding Eulerian coordi- nates. The key quantity describing the deformation in Eulerian coordinates is the inverse of the deformation, i.e. the reference map. The Eulerian model is formally constructed, and by reducing the GENERIC system to a damped Hamiltonian system, the isothermal limit is derived. A structure-preserving weak formulation is developed. As an example, the coupling of finite strain viscoelasticity and diffusion in a multiphase system governed by Lagrangian indicator functions is demonstrated. -
O. Pártl, E. Meneses Rioseco, Efficient numerical framework for geothermal energy production optimization in fracture-controlled reservoirs, Preprint no. 3169, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3169 .
Abstract, PDF (3112 kByte)
We describe an open-source numerical framework for the automated search for the placements of injection and production wells in hot fracture-controlled reservoirs that sustainably optimize geothermal energy production, where we consider deviated multiwell layouts (smart multiwell arrangement). This search is carried out via 3D simulations of groundwater flow and heat transfer. We model the reservoirs as discrete fracture networks (DFN) in which the fractures are 2D manifolds with polygonal boundaries embedded in a 3D porous medium. The wells are modeled via the immersed boundary method. The flow and heat transport in the DFN-matrix system are modeled by solving the balance equations for mass, momentum, and energy. The fully developed numerical framework combines the finite element method with semi-implicit time-stepping, algebraic flux correction, and approximation of the wells via the non-matching approach. To perform the optimization, we use various gradient- free algorithms. We present the results of verification and validation tests with DFNs of simple structure and realistic physical parameter values.
 Talks, Poster
Talks, Poster
-
J. Fuhrmann, Two point flux finite volume methods for mixture flows in porous media, Mixtures: Modeling, analysis and computing, February 5 - 7, 2025, Charles University, Faculty of Mathematics and Physics, Prag, Czech Republic, February 5, 2025.
-
V. John, Finite element methods respecting the discrete maximum principle for convection-diffusion equations, The International Conference on Multigrid and Multiscale Methods in Computational Science (IMG) 2025, February 3 - 5, 2025, King Abdullah University of Science and Technology (KAUST), Thuwal, Saudi Arabia, February 3, 2025.
-
CH. Merdon, Pressure-robustness for (nearly) incompressible flows, The ninth international conference on Ädvanced COmputational Methods in ENgineering and Applied Mathematics" (ACOMEN2025), MS9 Ädvanced Numerical Methods for Flow and Related Problems", September 15 - 19, 2025, Ghent University, University of Liège, Ghent, Belgium.
-
O. Pártl, Efficient numerical framework for fracture-controlled reservoir performance optimization, Leibniz MMS Days 2025, March 26 - 28, 2025, The Leibniz Research Network "Mathematical Modeling and Simulation", Leibniz Institute for Baltic Sea Research Warnemünde (IOW), March 27, 2025.
-
O. Pártl, Geothermal well placement optimization for sustainable energy production: New computational framework for fracture-controlled reservoirs, European Geothermal Congress (EGC), October 6 - 10, 2025, Zürich, Switzerland, October 8, 2025.
-
Z. Amer, Numerical methods for coupled drift-diffusion and Helmholtz models for laser applications, Leibniz MMS Days 2024, April 10 - 12, 2024, Leibniz Network "Mathematical Modeling and Simulation", Leibniz Institut für Verbundwerkstoffe GmbH (IVW), Kaiserslautern, April 11, 2024.
-
M. Demir, Pressure-robust approximation of the Navier--Stokes equations with coriolis force, 9th European Congress of Mathematics (9ECM), July 15 - 19, 2024, Congress of the European Mathematical Society, School of Engineering of the University of Seville, Spain, July 15, 2024.
-
M. Demir, Pressure-robust approximation of the incompressable Navier--Stokes equationsin a rotating frame of reference, Exploring Scientific Research: Workshop for Early Career Researchers, November 11 - 12, 2024, Gulf University for Science and Technology, Center for Applied Mathematics and Bioinformatics, Kuwait-Stadt, Kuwait, November 11, 2024.
-
M. Demir, Time filtered second order backward Euler method for EMAC formulation of Navier--Stokes equations, 20th Annual Workshop on Numerical Methods for Problems with Layer Phenomena, May 23 - 24, 2024, University of Cyprus, Department of Mathematics and Statistics, Protaras, Cyprus, May 24, 2024.
-
M. Zainelabdeen, Physics-informed neural networks for convection-dominated convection-diffusion problems, 20th Annual Workshop on Numerical Methods for Problems with Layer Phenomena, May 22 - 25, 2024, Department of Mathematics and Statistics, University of Cyprus, Protaras, May 24, 2024.
-
M. Zainelabdeen, Physics-informed neural networks for convection-dominated convection-diffusion problems, International Conference on Boundary and Interior Layers, BAIL 2024, June 10 - 14, 2024, University of A Coruña, Department of Mathematic, Spain, June 11, 2024.
-
A. Caiazzo, Validation of an open-source lattice Boltzmann solver (OpenLB) for the simulation of airflow over diary building, Leibniz MMS Days 2024, April 10 - 12, 2024, Leibniz Network "Mathematical Modeling and Simulation", Leibniz Institut für Verbundwerkstoffe GmbH (IVW), Kaiserslautern, April 11, 2024.
-
V. John, Finite element methods respecting the discrete maximum principle for convection-diffusion equations, International Conference on Latest Advances in Computational and Applied Mathematics (LACAM) 2024, February 21 - 24, 2024, Indian Institute of Science Education and Research, Thiruvananthapuram, Kerala, India, February 21, 2024.
-
V. John, Finite element methods respecting the discrete maximum principle for convection-diffusion equations, Mathematical Fluid Mechanics In 2024, August 19 - 23, 2024, Czech Academy of Sciences, Institute of Mathematics, Prague, Czech Republic, August 21, 2024.
-
V. John, Finite element methods respecting the discrete maximum principle for convection-diffusion equations, Trends in Scientific Computing -- 30 Jahre Wissenschaftliches Rechnen in Dortmund, May 21 - 22, 2024, Technische Universität Dortmund, Fakultät für Mathematik, LSIII, May 21, 2024.
-
V. John, On two modeling issues in aortic blood flow simulations, Seminar of Dr. Nagaiah Chamakuri, Scientific Computing Group (SCG), School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram, Kerala, India, February 20, 2024.
-
V. John, On using machine learning techniques for the numerical solution of convection-diffusion problems, ALGORITMY 2024, Central-European Conference on Scientific Computing, Minisymposium ``Numerical Methods for Convection-dominated Problems'', March 16 - 20, 2024, Department of Mathematics and Descriptive Geometry, Slovak University of Technology in Bratislava, Podbanske, Slovakia, March 19, 2024.
-
V. John, On using machine learning techniques for the numerical solution of convection-diffusion problems, Seminar of Prof. Sashikumaar Ganesan, Indian Institute of Science Bangalore, Department of Computational and Data Sciences, Bangalore, India, February 13, 2024.
-
CH. Merdon, Mass-conservative reduced basis approach for heterogeneous catalysis, Leibniz MMS Days 2024, Kaiserslautern, April 10 - 12, 2024.
-
CH. Merdon, Mass-conservative reduced basis approach for heterogeneous catalysis, Leibniz MMS Days 2024, April 10 - 12, 2024, Leibniz Network "Mathematical Modeling and Simulation", Leibniz Institut für Verbundwerkstoffe GmbH (IVW), Kaiserslautern.
-
CH. Merdon, Pressure-robustness in Navier--Stokes finite element simulations, 10th International Conference on Computational Methods in Applied Mathematics (CMAM-10), June 10 - 14, 2024, Universität Bonn, Institut für Numerische Simulation, June 11, 2024.
-
CH. Merdon, Pressure-robustness in Navier--Stokes finite elements simulations, Wissenschaftlicher Beirat, WIAS Berlin, September 27, 2024.
-
CH. Merdon, Pressure-robustness in the context of the weakly compressible Navier--Stokes equations, The Chemnitz Finite Element Symposium 2024, September 9 - 11, 2024, Technische Universität Chemnitz, September 9, 2024.
-
O. Pártl, Fracture-controlled reservoir performance optimization via 3D numerical modeling and simulation, Leibniz MMS Days 2024, April 10 - 12, 2024, Leibniz Network "Mathematical Modeling and Simulation", Leibniz Institut für Verbundwerkstoffe GmbH (IVW), Kaiserslautern, April 11, 2024.
-
O. Pártl, Optimization of geothermal energy production from fracture-controlled reservoirs via 3D numerical modeling and simulation, General Assembly 2024 of the European Geosciences Union (EGU), April 14 - 19, 2024, European Geosciences Union (EGU), Wien, Austria, April 15, 2024, DOI 10.5194/egusphere-egu24-4164 .
-
F. Romor, Efficient numerical resolution of parametric partial differential equations on solution manifolds parametrized by neural networks, 9th European Congress on Computational Methods in Applied Sciences and Engineering, June 3 - 7, 2024, ECCOMAS, scientific organization, Lissabon, Portugal, June 4, 2024.
-
D. Runge, Mass-conservative reduced basis approach for heterogeneous catalysis, Leibniz MMS Days 2024, Kaiserslautern, April 10 - 12, 2024.
-
S. Katz, Impact of turbulence modeling on the full and reduced simulations of aortic blood flow, 22nd Computational Fluids Conference (CFC 2023), April 25 - 28, 2023, International Association for Computational Mechanics (IACM), Cannes, France, April 28, 2023.
-
D. Runge, Mass-conservative reduced basis approach for convection-diffusion equations with non-linear boundary reaction conditions, Leibniz MMS Days 2023, Leibniz Network "Mathematical Modeling and Simulation", Leibniz Institute for Agricultural Engineering and Bioeconomy Potsdam (ATB), Potsdam, April 18, 2023.
-
A. Selahi, A finite-element-solver for coupled domains in rust, SIAM Conference on Computational Science and Engineering (CSE23), Amsterdam, Netherlands, February 26 - March 3, 2023.
-
D. Frerichs-Mihov, On deep learning techniques for solving convection-dominated convection-diffusion equations, 10th International Congress on Industrial and Applied Mathematics (ICIAM), Minisymposium 00747 ''Analysis and Numerics on Deep Learning Based Methods for Solving PDEs'', August 20 - 25, 2023, Waseda University, Tokyo, Japan, August 23, 2023.
-
D. Frerichs-Mihov, Using deep learning techniques for solving convection-dominated convection-diffusion equations, 22nd Computational Fluids Conference (CFC 2023), April 25 - 28, 2023, International Association for Computational Mechanics (IACM), Cannes, France, April 28, 2023.
-
V. John, A SUPG-stabilized POD-ROM method for convection-diffusion-reaction problems (online talk), Numerical Analysis of Galerkin ROMs seminar series (Online Event), February 28, 2023.
-
V. John, Finite element methods respecting the discrete maximum principle for convection-diffusion equations I, 19th Workshop on Numerical Methods for Problems with Layer Phenomena, Charles University, Faculty of Mathematics and Physics, Department of Numerical Mathematics, Prague, Czech Republic, May 26, 2023.
-
V. John, On recent topics in the finite element analysis of convection-diffusion problems (online talk), Numerical Analysis Seminar (Hybrid Event), University of Waterloo, Applied Mathematics, Canada, April 11, 2023.
-
O. Pártl, A computational framework for sustainable geothermal energy production in fracture-controlled reservoir based on well placement optimization, Leibniz MMS Days 2023, Potsdam, April 17, 2023.
-
O. Pártl, Finite element methods respecting the discrete maximum principle for convection-diffusion equations III, 19th Workshop on Numerical Methods for Problems with Layer Phenomena, Charles University, Faculty of Mathematics and Physics, Department of Numerical Mathematics, Prague, Czech Republic, May 26, 2023.
-
V. John, Finite element methods respecting the discrete maximum principle for convection-diffusion equations I, International Conference on Boundary and Interior Layers, November 28 - December 2, 2022, Universidad de Buenos Aires, Argentina, December 1, 2022.
-
P. Farrell, Modelling and simulation of the lateral photovoltage scanning method (online talk), European Conference on Mathematics for Industry (ECMI2021), MSOEE: ``Mathematical Modeling of Charge Transport in Graphene and Low dimensional Structures'' (Online Event), April 13 - 15, 2021, Bergische Universität Wuppertal, April 13, 2021.
-
P. Farrell, D. Peschka, Challenges in drift-diffusion semiconductor simulations, Finite Volumes for Complex Applications IX (Online Event), Bergen, Norway, June 15 - 19, 2020.
-
J. Fuhrmann, D.H. Doan, A. Glitzky, M. Liero, G. Nika, Unipolar drift-diffusion simulation of S-shaped current-voltage relations for organic semiconductor devices, Finite Volumes for Complex Applications IX (Online Event), Bergen, Norway, June 15 - 19, 2020.
-
V. John, On the provable convergence order for the kinetic energy of FEMs for the incompressible Navier--Stokes equations, 7th European Seminar on Computing (ESCO 2020) (Online Event), Pilsen, Czech Republic, June 8 - 12, 2020.
-
R. Lasarzik, Dissipative solutions in the context of the numerical approximation of nematic electrolytes (online talk), Oberseminar Numerik, Universität Bielefeld, Fakultät für Mathematik, June 23, 2020.
-
A. Linke, Ch. Merdon, On high-order pressure-robust space discretisations, their advantages for incompressible high Reynolds number generalised Beltrami flows and beyond, Einstein Semester on Energy-based Mathematical Methods for Reactive Multiphase Flows: Kick-off Conference (Online Event), Berlin, October 26 - 30, 2020.
-
A. Linke, Ch. Merdon, On the significance of pressure-robustness for the space discretization of incompressible high Reynolds number flows, Finite Volumes for Complex Applications IX (Online Event), Bergen, Norway, June 15 - 19, 2020.
-
H. Si, Adaptive exponential time integration of the Navier--Stokes equations, 3rd AIAA Sonic Boom Prediction Workshop, January 5 - 10, 2020, American Institute of Aeronautics and Astronautics SciTech Forum, Orlando, Florida, USA, January 10, 2020.
-
D. Peschka, Mathematical modeling and simulation of substrate-flow interaction using generalized gradient flow, Begutachtungskolloquium für die Anträge des SPP 2171 ``Dynamische Benetzung flexibler, adaptiver und schaltbarer Oberflächen'', Mainz, February 7 - 8, 2019.
-
A. Caiazzo, Data assimilation in one-dimensional hemodynamics, European Conference on Numerical Mathematics and Advanced Applications (ENUMATH 2019), Minisymposium 36 ``Data-Driven Computational Fluid Dynamics (Part 2)'', September 30 - October 4, 2019, Eindhoven University of Technology, Netherlands, October 1, 2019.
-
A. Caiazzo, Geothermal reservoir: Modeling, simulation and optimization for district heating in hot sedimentary acquires, Leibniz MMS Days 2019, March 20 - 22, 2019, Universität Rostock , Leibniz-Institut für Atmosphärenphysik, Kühlungsborn, March 22, 2019.
-
V. John, Algebraic finite element stabilizations for convection-diffusion equations, Workshop on Computational Modeling and Numerical Analysis (WCMNA 2019), February 25 - 28, 2019, Laboratório Nacional de Computação Científica, Petrópolis, Brazil, February 26, 2019.
-
V. John, Algebraic finite element stabilizations for convection-diffusion equations, Workshop ''Towards Computable Flows'', April 26 - 27, 2019, Georg-August-Universität Göttingen, Institut für Numerische und Angewandte Mathematik, April 26, 2019.
-
V. John, Finite element methods for incompressible flows, Workshop on Computational Modeling and Numerical Analysis (WCMNA 2019), February 25 - 28, 2019, Laboratório Nacional de Computação Científica, Petrópolis, Brazil.
-
V. John, Finite elements for scalar convection-dominated equations and incompressible flow problems -- A never ending story?, Conference on Applied Mathematics, August 19 - 21, 2019, Lahore University of Management Sciences, Pakistan, August 19, 2019.
-
V. John, Finite elements for scalar convection-dominated equations and incompressible flow problems -- A never ending story?, Indo-German Conference on Computational Mathematics (IGCM), December 2 - 4, 2019, Indian Institute of Science, Department of Computer and Data Sciences, Bangalore, India, December 3, 2019.
-
V. John, On $L^2(Omega)$ estimates for finite element methods for evolutionary convection-dominated problems, PIMS-Germany Workshop on Discretization of Variational Eigenvalue and Flow Problems, June 24 - 26, 2019, Universität Heidelberg, June 25, 2019.
-
V. John, Variational Multiscale (VMS) methods for the simulation of turbulent incompressible flows, University of Groningen, Bernoulli Institute, Computational Mechanics & Numerical Mathematics, Netherlands, September 23, 2019.
-
V. John, Variational Multiscale (VMS) methods for the simulation of turbulent incompressible flows, Indian Institute of Science, Department of Computational and Data Science, Bangalore, India, November 28, 2019.
-
N. Alia, Modeling and optimization of a gas-stirred liquid flow for steelmaking processes, The 20th European Conference on Mathematics for Industry (ECMI), MS27: MSO for steel production and manufacturing, June 18 - 22, 2018, University Budapest, Institute of Mathematics at Eötvös Loránd, Hungary, June 19, 2018.
-
R. Ahrens, F. Anker, C. Bartsch, A. Voigt, V. Wiedmeyer, K. Sundmacher, V. John, S. Le Borne, Advanced numerical methods for the simulation of population balance systems, 6th International Conference on Population Balance Modelling (PBM2018), Ghent University, Belgium, May 7 - 9, 2018.
-
L. Blank, A robust finite element method for the Brinkman problem, 13th International Workshop on Variational Multiscale and Stabilized Finite Elemements, Weierstraß-Institut, Berlin, December 5, 2018.
-
L. Blank, An unconditionally stable, low order, and robust finite element method for the numerical simulation of porous media flow, 39th Northern German Colloquium on Applied Analysis and Numerical Mathematics (NoKo 2018), June 1 - 2, 2018, Technische Universität Braunschweig, June 2, 2018.
-
C. Bartsch, V. John, R.I.A. Patterson, A new mixed stochastic-deterministic simulation approach to particle populations in fluid flows, 6th International Conference on Population Balance Modelling (PBM2018), Ghent University, Belgium, May 7 - 9, 2018.
-
A. Caiazzo, A penalty-free Nitsche method for the Stokes, Darcy and Brinkman problems, Universität Augsburg, Lehrstuhl für Numerische Mathematik, May 15, 2018.
-
A. Caiazzo, Mathematical modeling and simulations of geothermal reservoirs, 16th European Finite Element Fair (EFEF 2018), June 8 - 9, 2018, Universität Heidelberg,, June 8, 2018.
-
A. Caiazzo, Mathematical modeling and simulations of geothermal reservoirs, Leibniz-Institut für Angewandte Geophysik, Hannover, November 7, 2018.
-
A. Caiazzo, Multiscale and reduced-order modeling of biphasic materials with application to tissue elastography, Rheinische Friedrich-Wilhelms-Universität Bonn, Institut für Numerische Simulation, November 23, 2018.
-
A. Caiazzo, Multiscale modeling of individual-based cancer models with arbitrary vasculature and fiber structure, 6th European Conference on Computational Mechanics, 7th European Conference on Computational Fluid Dynamics (ECCM-ECFD 2018), June 11 - 15, 2018, University of Glasgow, UK, June 12, 2018.
-
A. Caiazzo, Robust open boundary conditions and efficient data assimilation in multiscale hemodynamics, International Symposium ``Modeling, Simulation and Optimization of the Cardiovascular System'', October 22 - 24, 2018, Universität Magdeburg, October 22, 2018.
-
A. Caiazzo, Towards the personalization of (1D) blood-flow simulations, University of Amsterdam, Computational Science Lab, Netherlands, September 21, 2018.
-
V. John, A new mixed stochastic-deterministic simulation approach for particle populations in fluid flows, 6th European Seminar on Computing (ESCO), June 3 - 8, 2018, University of West Bohemia, Pilsen, Czech Republic, June 6, 2018.
-
V. John, Angewandte Mathematik für Strömungssimulationen, Martin-Luther-Universität Halle, Fachbereich Mathematik, October 27, 2018.
-
V. John, Finite elements for scalar convection-dominated equations and incompressible flow problems -- A never ending story?, International Conference of Boundary and Interior Layers (BAIL 2018), June 18 - 22, 2018, University of Strathclyde, Glasgow, Scotland, UK, June 18, 2018.
-
V. John, Variational Multiscale (VMS) methods for the simulation of turbulent incompressible flows, University of Strathclyde, Department of Mathematics and Statistics, Glasgow, UK, November 14, 2018.
-
A. Linke, On high-order pressure-robust space discretisations, their advantages for incompressible high Reynolds number generalised Beltrami flows and beyond, 13th International Workshop on Variational Multiscale and Stabilized Finite Elemements, Weierstraß-Institut, Berlin, December 5, 2018.
-
A. Linke, On the role of the Helmholtz--Hodge projector for a novel pressure-robust discretization theory for the incompressible Navier--Stokes equations, The University of Texas at Austin, Institute for Computational Engineering and Scienses, USA, September 18, 2018.
-
A. Linke, On the role of the Helmholtz--Leray projector for a novel pressure-robust discretization theory for the incompressible Navier--Stokes equations, Workshop ``Finite Element Exterior Calculus (FEEC) and High Order Methods'', June 4 - 6, 2018, University of Oslo, Faculty of Mathematics and Natural Sciences, Norway, June 6, 2018.
-
A. Linke, On the role of the Helmholtz--Leray projector for a novel pressure-robust discretization theory for the incompressible Navier--Stokes equations, Georg-August-Universität Göttingen, Institut für Numerische und Angewandte Mathematik, January 23, 2018.
-
A. Linke, On the role of the Helmholtz--Leray projector for a novel pressure-robust discretization theory for the incompressible Navier--Stokes equations, Aix Marseille Université, Institut de Mathématiques, France, April 3, 2018.
-
A. Linke, On the role of the Helmholtz--Leray projector for a novel pressure-robust discretization theory for the incompressible Navier--Stokes equations, Clemson University, Department of Mathematical Sciences, South Carolina, USA, August 17, 2018.
-
A. Linke, On the role of the Helmholtz--Leray projector in the space discretization of the Navier--Stokes equations, 3rd Leibniz MMS Days 2018, February 28 - March 2, 2018, Wissenschaftszentrum Leipzig, March 1, 2018.
-
A. Linke, Towards pressure-robust mixed methods for the incompressible Navier--Stokes equations, 89th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2018), March 19 - 23, 2018, Technische Universität München, March 22, 2018.
-
A. Linke, User talk: Pressure-robust space discretization for the incompressible Navier--Stokes equations, 2nd NGSolve User Meeting, July 4 - 6, 2018, Georg-August-Universität Göttingen, Institut für Numerische und Angewandte Mathematik, July 5, 2018.
-
U. Wilbrandt, Iterative subdomain methods for the Stokes--Darcy coupling, 6th European Conference on Computational Mechanics, 7th European Conference on Computational Fluid Dynamics (ECCM-ECFD 2018), June 11 - 15, 2018, University of Glasgow, UK, June 11, 2018.
-
T. Keil, Simulation and control of a nonsmooth Cahn--Hilliard Navier--Stokes system with variable fluid densities (with Carmen Graessle), Annual Meeting of the DFG Priority Programme 1962, October 9 - 11, 2017, Kremmen (Sommerfeld), October 11, 2017.
-
T. Keil, Strong stationarity conditions for the optimal control of a Cahn--Hilliard--Navier--Stokes system, 14th International Conference on Free Boundary Problems: Theory and Applications, Theme Session 8 ``Optimization and Control of Interfaces'', July 9 - 14, 2017, Shanghai Jiao Tong University, China, July 10, 2017.
-
CH. Merdon, A novel concept for the discretisation of the coupled Nernst--Planck--Poisson--Navier--Stokes system, 14th Symposium on Fuel Cell Modelling and Experimental Validation (MODVAL 14), March 2 - 3, 2017, Karlsruher Institut für Technologie, Institut für Angewandte Materialien, Karlsruhe, Germany, March 3, 2017.
-
CH. Merdon, Druckrobuste Finite-Elemente-Methoden für die Navier-Stokes-Gleichungen, Universität Paderborn, Institut für Mathematik, April 25, 2017.
-
CH. Merdon, Pressure-robustness in mixed finite element discretisations for the Navier--Stokes equations, Universität des Saarlandes, Fakultät für Mathematik und Informatik, July 12, 2017.
-
D. Peschka, Modelling and simulation of suspension flow, Graduate Seminar PDE in the Sciences, Universität Bonn, Institut für Angewandte Mathematik, January 20, 2017.
-
N. Kumar, J.H.M. Ten Thije Boonkkamp, B. Koren, A. Linke, A nonlinear flux approximation scheme for the viscous Burgers equation, 8th International Symposium on Finite Volumes for Complex Applications (FVCA 8), Université Lille 1, Villeneuve d'Ascq, France, June 12 - 16, 2017.
-
N. Ahmed, Higher-order discontinuous Galerkin time discretizations for the evolutionary Navier--Stokes equations, Technische Universität Dresden, Institut für Numerische Mathematik, March 9, 2017.
-
N. Ahmed, On really locking-free mixed finite element methods for the transient incompressible Stokes equations, CASM International Conference on Applied Mathematics, May 22 - 24, 2017, Lahore University of Management Sciences, Centre for Advanced Studies in Mathematics, Pakistan, May 22, 2017.
-
C. Bartsch, ParMooN -- A parallel finite element solver, Part I, Indian Institute of Science, Supercomputer Education and Research Centre, Bangalore, India, March 16, 2017.
-
M. Hintermüller, Optimal control of multiphase fluids based on non smooth models, 14th International Conference on Free Boundary Problems: Theory and Applications, Theme Session 8 ``Optimization and Control of Interfaces'', July 9 - 14, 2017, Shanghai Jiao Tong University, China, July 10, 2017.
-
M. Hintermüller, Total variation diminishing Runge--Kutta methods for the optimal control of conservation laws: Stability and order-conditions, SIAM Conference on Optimization, Minisymposium MS111 ``Optimization with Balance Laws on Graphs'', May 22 - 25, 2017, Vancouver, British Columbia, Canada, May 25, 2017.
-
V. John, Analytical and numerical results for algebraic flux correction schemes, 12th International Workshop on Variational Multiscale and Stabilization Methods (VMS-2017), April 26 - 28, 2017, Edificio Celestino Mutis, Campus Reina Mercedes, Sevilla, Spain, April 26, 2017.
-
V. John, Finite element methods for incompressible flow problems, May 14 - 18, 2017, Beijing Computational Science Research Center, Applied and Computational Mathematics, China.
-
V. John, Finite elements for scalar convection-dominated equations and incompressible flow problems --- A never ending story?, 30th Chemnitz FEM Symposium, September 25 - 27, 2017, Bundesinstitut für Erwachsenenbildung, St. Wolfgang / Strobl, Austria, September 27, 2017.
-
V. John, Variational multiscale (VMS) methods for the simulation of turbulent incompressible flows, CDS: Computational Science Symposium, March 16 - 18, 2017, Indian Institute of Science, Department of Computer and Data Sciences, Bangalore, India, March 16, 2017.
-
V. John, Variational multiscale (VMS) methods for the simulation of turbulent incompressible flows, Mahindra École Centrale, School of Natural Sciences, Hyderabad, India, March 9, 2017.
-
V. John, Variational multiscale (VMS) methods for the simulation of turbulent incompressible flows, Chinese Academy of Sciences, Academy of Mathematics and Systems Science, Beijing, May 10, 2017.
-
V. John, Variational multiscale (VMS) methods for the simulation of turbulent incompressible flows, Peking University, School of Mathematical Sciences, Beijing, China, May 11, 2017.
-
A. Linke, Towards pressure-robust mixed methods for the incompressible Navier--Stokes equations, 12th International Workshop on Variational Multiscale and Stabilization Methods (VMS-2017), April 26 - 28, 2017, Edificio Celestino Mutis, Campus Reina Mercedes, Sevilla, Spain, April 27, 2017.
-
CH. Merdon, Pressure-robust finite element methods for the Navier--Stokes equations, GAMM Workshop on Numerical Analysis, November 1 - 2, 2017, Rheinisch-Westfälische Technische Hochschule Aachen, November 2, 2017.
-
CH. Merdon, Pressure-robust mixed finite element methods for the Navier--Stokes equations, scMatheon Workshop RMMM 8 - Berlin 2017, Reliable Methods of Mathematical Modeling, July 31 - August 3, 2017, Humboldt-Universität zu Berlin, August 2, 2017.
-
U. Wilbrandt, ParMooN -- A parallel finite element solver, Part II, Indian Institute of Science, Supercomputer Education and Research Centre, Bangalore, India, March 16, 2017.
-
N. Alia, V. John, Optimal control of ladle stirring, 1st Leibniz MMS Mini Workshop on CFD & GFD, WIAS Berlin, September 8 - 9, 2016.
-
CH. Merdon, J. Fuhrmann, A. Linke, A.A. Abd-El-Latif, M. Khodayari, P. Reinsberg, H. Baltruschat, Inverse modelling of thin layer flow cells and RRDEs, The 67th Annual Meeting of the International Society of Electrochemistry, Den Haag, Netherlands, August 21 - 26, 2016.
-
D. Peschka, A free boundary problem for the flow of viscous liquid bilayers, ERC Workshop on Modeling Materials and Fluids using Variational Methods, February 22 - 26, 2016, WIAS Berlin, Berlin, February 26, 2016.
-
D. Peschka, Multi-phase flows with contact lines: Solid vs liquid substrates, Industrial and Applied Mathematics Seminar, University of Oxford, Mathematical Institute, UK, October 27, 2016.
-
N. Ahmed, A review of VMS methods for the simulation of turbulent incompressible flows, International Conference on Differential Equations and Applications, May 26 - 28, 2016, Lahore University of Management Sciences, Pakistan, May 27, 2016.
-
N. Ahmed, On the grad-div stabilization for the steady Oseen and Navier--Stokes evaluations, International Conference of Boundary and Interior Layers (BAIL 2016), August 15 - 19, 2016, Beijing Computational Science Research Center, Beijing, China, August 15, 2016.
-
V. John, A review of variational multiscale methods for the simulation of turbulent incompressible flows, 15th Mathematics of Finite Elements and Applications, June 14 - 17, 2016, Brunel University London, London, UK, June 17, 2016.
-
V. John, A review of variational multiscale methods for the simulation of turbulent incompressible flows, ``Variational Multiscale and Stabilization Methods'' (VMS2016), March 16 - 18, 2016, Otto-von-Guericke Universität Magdeburg, Magdeburg, March 17, 2016.
-
V. John, A review of variational multiscale methods for the simulation of turbulent incompressible flows, International Conference of Boundary and Interior Layers (BAIL 2016), August 15 - 19, 2016, Beijing Computational Science Research Center, Beijing, China, August 15, 2016.
-
V. John, A review of variational multiscale methods for the simulation of turbulent incompressible flows, 7th American Mathematical Society Meeting, Special Session on Above and Beyond Fluid Flow Studies, October 8 - 9, 2016, Denver, Colorado, USA, October 9, 2016.
-
V. John, A survey on the analysis and numerical analysis of some turbulence models, Technische Universität Darmstadt, Fachbereich Mathematik, January 20, 2016.
-
V. John, Ein weites Feld -- Wissenschaftliche Beiträge von Prof. Dr. Lutz Tobiska, Festkolloquium aus Anlass des 65. Geburtstags von Prof. Dr. Lutz Tobiska, Universität Magdeburg, Institut für Analysis und Numerik, March 31, 2016.
-
V. John, On the divergence constraint in mixed finite element methods for incompressible flows, 5th European Seminar on Computing (ESCO 2016), June 5 - 10, 2016, Pilsen, Czech Republic, June 7, 2016.
-
V. John, On the divergence constraint in mixed finite element methods for incompressible flows, Beijing Computational Science Research Center, China, August 23, 2016.
-
V. John, The role of the pressure in finite element methods for incompressible flow problems, Summer School 2016 ``Fluids under Pressure'' and Workshop, August 29 - September 2, 2016, Nečas Center for Mathematical Modeling, Prague, Czech Republic.
-
CH. Merdon, Inverse modeling of thin layer flow cells for detection of solubility transport and reaction coefficients from experimental data, 17th Topical Meeting of the International Society of Electrochemistry Multiscale Analysis of Electrochemical Systems, May 31 - June 3, 2015, Saint Malo Congress Center, France, June 1, 2015.
-
N. Ahmed, Adaptive time step control with variational time stepping schemes for convection-diffusion-reaction equations, 26th Biennial Numerical Analysis Conference, June 23 - 26, 2015, University of Strathclyde, Glasgow, UK, June 23, 2015.
-
N. Ahmed, Higher order time stepping schemes, 13th European Finite Element Fair, June 5 - 6, 2015, Charles University in Prague, Praha, Czech Republic, June 5, 2015.
-
A. Caiazzo, Assessment of Kalman filtering for parameter identification in one-dimensional blood flow model, 4th International Conference on Computational & Mathematical Biomedical Engineering, June 29 - July 1, 2015, Ecole Normale Supérieure de Cachan, Cachan, France, June 29, 2015.
-
V. John, S. Rockel, S. Sobolev, Viscoelastic mantle flow --- Numerical modeling of geological phenomena, 4th Annual GEOSIM Workshop, Potsdam, November 17 - 18, 2015.
-
U. Wilbrandt, Classical iterative subdomain methods for the Stokes--Darcy problem, Rheinisch-Westfälische Technische Hochschule Aachen, Institut für Geometrie und Praktische Mathematik, Aachen, June 11, 2015.
-
A. Linke, On the role of the Helmholtz decomposition in mixed methods for incompressible flows, International Conference of Boundary and Interior Layers (BAIL 2014), September 15 - 19, 2014, Carles University Prague, Czech Republic, September 17, 2014.
-
A. Linke, Ch. Merdon, Optimal and pressure-independent $L^2$ velocity error estimates for a modified Crouzeix--Raviart element with BDM reconstructions, The International Symposium of Finite Volumes for Complex Applications VII (FVCA 7), Berlin-Brandenburgische Akademie der Wissenschaften, June 15 - 20, 2014.
-
A. Linke, Ein neues Konstruktionsprinzip zur divergenzfreien Diskretisierung der inkompressiblen Navier-Stokes-Gleichungen, Ruhr-Universität Bochum, Fakultät für Mathematik, July 17, 2014.
-
A. Linke, On the role of the Helmholtz decomposition in incompressible flows and a new variational crime, NonLinear PDE and Applications: Theoretical and Numerical Study, May 5 - 7, 2014, Abdelmalek Essadi University, Tanger, Morocco, May 6, 2014.
-
A. Linke, On the role of the Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime, Technische Universität Wien, Institut für Analysis und Scientific Computing, Austria, April 2, 2014.
-
A. Linke, On the role of the Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime, Technische Universität Hamburg-Harburg, Institut für Mathematik, January 7, 2014.
-
A. Linke, On the role of the Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime, Friedrich-Alexander-Universität Erlangen-Nürnberg, Fachbereich Mathematik, November 20, 2014.
-
A. Linke, On the role of the Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime, Georg-August-Universität Göttingen, Institut für Numerische und Angewandte Mathematik, December 9, 2014.
-
V. John, On isogeometric analysis for convection-diffusion and Navier--Stokes equations, International Conference of Boundary and Interior Layers (BAIL 2014), September 15 - 19, 2014, Carles University Prague, Czech Republic, September 15, 2014.
-
J. Fuhrmann, A. Linke, Ch. Merdon, M. Khodayari, H. Baltruschat, Detection of solubility, transport and reaction coefficients from experimental data by inverse modeling of thin layer flow cells, 65th Annual Meeting of the International Society of Electrochemistry, Lausanne, Switzerland, August 31 - September 5, 2014.
-
J. Fuhrmann, A. Linke, Ch. Merdon, Coupling of fluid flow and solute transport using a divergence-free reconstruction of the Crouzeix--Raviart element, The International Symposium of Finite Volumes for Complex Applications VII (FVCA 7), Berlin-Brandenburgische Akademie der Wissenschaften, June 15 - 20, 2014.
-
J. Fuhrmann, Activity based finite volume methods for generalised Nernst--Planck--Poisson systems, The International Symposium of Finite Volumes for Complex Applications VII (FVCA 7), Berlin-Brandenburgische Akademie der Wissenschaften, June 15 - 20, 2014.
-
J. Fuhrmann, Voronoi finite volume methods, XVI. Mathematica-Tag, Berlin, December 9, 2014.
-
V. John, S. Rockel, S. Sobolev, Viscoelastic mantle flow, 3rd Annual GEOSIM Workshop, Potsdam, November 13 - 14, 2014.
-
V. John, Finite element methods for incompressible flow problems, Indian National Program on Differential Equations -- Theory, Computation, and Applications (NPDE-TCA) Advanced Workshop on Finite Element Methods for Navier--Stokes Equations, September 8 - 12, 2014, Indian Institute of Science, Numerical Mathematics & Scientific Computing, Bangalore.
-
V. John, Numerical methods for convection-dominated equations, 2nd Workshop ``Populationsbilanzen'' of the DFG Priority Program SPP 1679 ``Dyn-Sim-FP -- Dynamic Simulation of Interconnected Solids Processes'', May 6 - 7, 2014, Technische Universität Hamburg-Harburg, May 6, 2014.
-
V. John, On the simulation of mantle convection, Symposium on Simulation and Optimization of Extreme Fluids, November 10 - 12, 2014, Internationales Wissenschaftsforum Heidelberg, November 12, 2014.
-
V. John, Turbulent flows and their numerical simulation, Humboldt Kolleg on Interdisciplinary Science: Catalyst for Sustainable Progress, September 4 - 6, 2014, Indian Institute of Science, Numerical Mathematics & Scientific Computing, Bangalore, September 5, 2014.
-
U. Wilbrandt, Iterative subdomain methods for Stokes--Darcy problems, Norddeutsches Kolloquium über Angewandte Analysis und Numerische Mathematik (NoKo), May 9 - 10, 2014, Christian-Albrechts-Universität zu Kiel, May 9, 2014.
-
V. John, On recent analytical and numerical investigations of the SUPG method, Advances in Computational Mechanics (ACM 2013) -- A Conference Celebrating the 70th Birthday of Thomas J.R. Hughes, February 24 - 27, 2013, San Diego, USA, February 27, 2013.
-
A. Linke, Coupled flows and poor mass conservation, Workshop ``Complex grids and fluid flows, conclusion of VFSitCom, National Research Project'', April 2 - 4, 2012, Rhône-Alpes, Lyon, France, April 3, 2012.
-
V. John, On reduced order modeling methods for incompressible flows based proper orthogonal decomposition, 6th Variational Multiscale Methods Workshop (VMS 2012), June 27 - 29, 2012, Christian-Albrechts-Universität zu Kiel, June 28, 2012.
-
V. John, On the analysis and numerical analysis of some turbulence models, Workshop ``Connections Between Regularized and Large-Eddy Simulation Methods for Turbulence'', May 14 - 17, 2012, Banff International Research Station for Mathematical Innovation and Discovery, Canada, May 15, 2012.
-
A. Glitzky, J.A. Griepentrog, Discrete Sobolev--Poincaré inequalities for Voronoi finite volume approximations, Finite Volumes for Complex Applications VI (FVCA 6), Prague, Czech Republic, June 6 - 10, 2011.
-
O.C. Suciu, A numerical method for the simulation of population balance systems with one internal coordinate, 8th International Conference on Large-Scale Scientific Computations, June 6 - 10, 2011, Bulgarian Academy of Sciences, Sozopol, June 7, 2011.
-
A. Caiazzo, J. Fuhrmann, V. John, Finite element-finite volume coupling for simulations of thin porous layer fuel cells, Workshop on Simulation of Flow in Porous Media and Applications in Waste Management and CO2 Sequestration, John Radon Institute for Computational and Applied Mathematics, Linz, Austria, October 3 - 7, 2011.
-
A. Caiazzo, Darcy-Stokes coupling for simulation of solute transport in thin-layer channel fuel cells, Workshop on Fluid Dynamics and Porous Media, September 12 - 14, 2011, University of Coimbra, Department of Mathematics, Portugal, September 13, 2011.
-
A. Caiazzo, Model reduction approaches for simulation of cardiovascular stents and pulmonary valve, Laboratory of Modeling and Scientific Computing, Department of Mathematics, Milan, Italy, October 27, 2011.
-
A. Caiazzo, Physical- and mathematical-based reduced order modeling in computational hemodynamics, Wroclaw University of Technology, Institute of Mathematics and Computer Science, Poland, November 16, 2011.
-
E. Schmeyer, V. John, R. Bordás, D. Thévenin, Referenzexperimente im Windkanal, numerische Simulation und Validierung, Annual Meeting 2010 of DFG Priority Program 1276 MetStröm, Zuse Institute Berlin, October 28 - 29, 2010.
-
O.C. Suciu, On numerical methods for simulation of 3D/4D of population balance system, SimParTurS Meeting, Max-Planck-Institut Leipzig, February 17, 2010.
-
V. John, A posteriori optimization of parameters in stabilized methods for convection-diffusion problems, BIRS Workshop ``Nonstandard Discretizations for Fluid Flows'', November 21 - 26, 2010, Banff International Research Station, Canada.
-
V. John, Error analysis of the SUPG finite element discretization of evolutionary convection-diffusion-reaction equations, 6th Variational Multiscale Methods Workshop (VMS 2010), May 27 - 28, 2010, Université de Pau et des Pays de l'Adour, France, May 27, 2010.
-
V. John, Error analysis of the SUPG finite element discretization of evolutionary convection-diffusion-reaction equations, International Conference of Boundary and Interior Layers (BAIL 2010), July 5 - 9, 2010, University of Zaragoza, Spain, July 8, 2010.
-
V. John, On the numerical simulation of population balance systems, Technische Universität Dresden, Fakultät Mathematik und Naturwissenschaften, April 20, 2010.
-
V. John, Variational multiscale methods for the simulation of turbulent flows, Volkswagen Wolfsburg, August 27, 2010.
-
M. Ehrhardt, J. Fuhrmann, A. Linke, Finite volume methods for the simulation of flow cell experiments, Workshop ``New Trends in Model Coupling --- Theory, Numerics & Applications'' (NTMC'09), Paris, France, September 2 - 4, 2009.
-
M. Ehrhardt, A high order finite element method for waves in periodic structures, 9th International Conference on Spectral and High Order Methods (ICOSAHOM09), Minisymposium ``High-order Methods for Linear and Nonlinear Wave Equations'', June 22 - 26, 2009, Norwegian University of Science and Technology, Trondheim, June 24, 2009.
-
V. John, A variational multiscale method for turbulent flow simulation with adaptive large scale space, Workshop on Computational Multiscale Modeling, November 26 - 27, 2009, University of Twente, Enschede, Netherlands, November 27, 2009.
-
V. John, On the numerical simulation of population balance systems, Karlsruher Institut für Technologie, Fakultät für Mathematik, December 9, 2009.
-
H.-Chr. Kaiser, Transient Kohn--Sham theory, Jubiläumssymposium ``Licht -- Materialien -- Modelle'' (100 Jahre Innovation aus Adlershof), Berlin-Adlershof, September 7 - 8, 2009.
-
K. Hoke, Numerical treatment of the Kohn--Sham system for semiconductor devices, Workshop on Mathematical Aspects of Transport in Mesoscopic Systems, Dublin, Ireland, December 4 - 7, 2008.
-
E. Bänsch, H. Berninger, U. Böhm, A. Bronstert, M. Ehrhardt, R. Forster, J. Fuhrmann, R. Klein, R. Kornhuber, A. Linke, A. Owinoh, J. Volkholz, Pakt für Forschung und Innovation: Das Forschungsnetzwerk ``Gekoppelte Strömungsprozesse in Energie- und Umweltforschung'', Show of the Leibniz Association ``Exzellenz durch Vernetzung. Kooperationsprojekte der deutschen Wissenschaftsorganisationen mit Hochschulen im Pakt für Forschung und Innovation'', Berlin, November 12, 2008.
-
M. Ehrhardt, O. Gloger, Th. Dietrich, O. Hellwich, K. Graf, E. Nagel, Level Set Methoden zur Segmentierung von kardiologischen MR-Bildern, 22. Treffpunkt Medizintechnik: Fortschritte in der medizinischen Bildgebung, Charité, Campus Virchow Klinikum Berlin, May 22, 2008.
-
A. Glitzky, Analysis of spin-polarized drift-diffusion models, 79th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2008), session ``Applied Analysis'', March 31 - April 4, 2008, University of Bremen, April 1, 2008.
-
A. Glitzky, Energy estimates for continuous and discretized reaction-diffusion systems in heterostructures, Annual Meeting of the Deutsche Mathematiker-Vereinigung 2008, minisymposium ``Analysis of Reaction-Diffusion Systems with Internal Interfaces'', September 15 - 19, 2008, Friedrich-Alexander-Universität Erlangen-Nürnberg, September 15, 2008.
-
A. Glitzky, Energy estimates for space and time discretized electro-reaction-diffusion systems, Conference on Differential Equations and Applications to Mathematical Biology, June 23 - 27, 2008, Université Le Havre, France, June 26, 2008.
-
H.-Chr. Kaiser, A drift-diffusion model for semiconductors with internal interfaces, Annual Meeting of the Deutsche Mathematiker-Vereinigung 2008, Minisymposium ``Analysis of Reaction-Diffusion Systems with Internal Interfaces'', September 15 - 19, 2008, Friedrich-Alexander-Universität Erlangen-Nürnberg, September 15, 2008.
-
H.-Chr. Kaiser, A thermodynamic approach to transient Kohn--Sham theory, 100th Statistical Mechanics Conference, December 13 - 18, 2008, Rutgers, The State University of New Jersey, New Brunswick, USA, December 16, 2008.
-
H.-Chr. Kaiser, On drift-diffusion Kohn--Sham theory, 79th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2008), session ``Applied Analysis'', March 31 - April 4, 2008, University of Bremen, April 1, 2008.
-
A. Glitzky, Energy estimates for reaction-diffusion processes of charged species, 6th International Congress on Industrial and Applied Mathematics (ICIAM), July 16 - 20, 2007, ETH Zürich, Switzerland, July 16, 2007.
-
H.-Chr. Kaiser, A drift-diffusion model of transient Kohn--Sham theory, First Joint International Meeting between the American Mathematical Society and the Polish Mathematical Society, Special Session ``Mathematics of Large Quantum Systems'', July 31 - August 3, 2007, University of Warsaw, Poland, August 3, 2007.
-
K. Gärtner, A. Glitzky, Th. Koprucki, Analysis and simulation of spin-polarized drift-diffusion models, Evaluation Colloquium of the DFG Priority Program SPP 1285 ``Semiconductor Spintronics'', Bad Honnef, December 14 - 15, 2006.
-
A. Glitzky, Energy estimates for electro-reaction-diffusion systems with partly fast kinetics, 6th AIMS International Conference on Dynamical Systems, Differential Equations & Applications, June 25 - 28, 2006, Université de Poitiers, France, June 27, 2006.
-
A. Glitzky, An application of the Implicit Function Theorem to stationary energy models for semiconductor devices, International Workshop ``Regularity for nonlinear and linear PDEs in nonsmooth domains'', September 4 - 7, 2005, Universität Stuttgart, Hirschegg, Austria, September 5, 2005.
-
A. Glitzky, Stationary energy models for semicoductor devices with incompletely ionized impurities, 2nd Joint Meeting of AMS, DMV, ÖMG, June 16 - 19, 2005, Johannes Gutenberg Universität, Mainz, June 19, 2005.
-
H. Gajewski, R. Hünlich, H.-Chr. Kaiser, M. Baro, Quantum mechanical and macroscopic models for optoelectronic devices, DFG Research Center sc Matheon, Technische Universität Berlin, July 19, 2004.
-
H. Gajewski, Zur Numerik des Ladungsträgertransports in Halbleiterbauelementen, Technische Universität München, Institut fär Technische Elektrophysik, February 5, 2004.
-
M. Baro, H. Gajewski, R. Hünlich, H.-Chr. Kaiser, Optoelektronische Bauelemente: mikroskopische & makroskopische Modelle, MathInside --- Überall ist Mathematik, event of the DFG Research Center ``Mathematics for Key Technologies'' on the occasion of the Open Day of Urania, Berlin, September 13, 2003 - December 3, 2004.
-
A. Glitzky, R. Hünlich, Stationary solutions of two-dimensional heterogeneous energy models with multiple species, Nonlocal Elliptic and Parabolic Problems, September 9 - 11, 2003, Bedlewo, Poland, September 10, 2003.
-
H.-Chr. Kaiser, Classical solutions of van Roosbroeck's equations with discontinuous coefficients and mixed boundary conditions on two-dimensional space domains, 19th GAMM Seminar Leipzig on High-dimensional problems --- Numerical treatment and applications, January 23 - 25, 2003, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, January 25, 2003.
 External Preprints
External Preprints
-
C.K. Macnamara, I. Ramis-Conde, T. Lorenzi, A. Caiazzo, An agent-based modelling framework for tumour growth incorporating mechanical and evolutionary aspects of cell dynamics, Preprint no. bioRxiv:596685, Cold Spring Harbor Laboratory, 2024, DOI 10.1101/2024.05.30.596685 .
Abstract
We develop an agent-based modelling framework for tumour growth that in-corporates both mechanical and evolutionary aspects of the spatio-temporal dynamics of cancer cells. In this framework, cells are regarded as viscoelastic spheres that interact with other neighbouring cells through mechanical forces. The phenotypic state of each cell is described by the level of expression of an hypoxia-inducible factor that regulates the cellular response to available oxygen. The rules that govern proliferation and death of cells in different phenotypic states are then defined by integrating mechanical constraints and evolutionary principles. Computational simulations of the model are carried out under a variety of scenarios corresponding to different intra-tumoural distributions of oxygen. The results obtained, which indicate excellent agreement between simulation outputs and the results of formal analysis of phenotypic selection, recapitulate the emergence of stable phenotypic heterogeneity among cancer cells driven by inhomogeneities in the intra-tumoural distribution of oxygen. This article is intended to present a proof of concept for the ideas underlying the proposed modelling framework, with the aim to apply the related modelling methods to elucidate specific aspects of cancer progression in the future. -
R. Araya, A. Caiazzo, F. Chouly, Stokes problem with slip boundary conditions using stabilized finite elements combined with Nitsche, Preprint no. arXiv:2404.08810, Cornell University, 2024, DOI 10.48550/arXiv.2404.08810 .
Abstract
We discuss how slip conditions for the Stokes equation can be handled using Nitsche method, for a stabilized finite element discretization. Emphasis is made on the interplay between stabilization and Nitsche terms. Well-posedness of the discrete problem and optimal convergence rates, in natural norm for the velocity and the pressure, are established, and illustrated with various numerical experiments. The proposed method fits naturally in the context of a finite element implementation while being accurate, and allows an increased flexibility in the choice of the finite element pairs. -
TH. Belin, P. Lafitte-Godillon, V. Lescarret, J. Fuhrmann, C. Mascia, hrefhttps://hal.science/hal-04647129/file/main_article_HAL.pdfEntropy solutions of a diffusion equation with discontinuous hysteresis and their finite volume approximation, Preprint no. hal-04647129, HAL (Hyper Articles en Ligne) open science, National Center for Scientific Research (CNRS), Inria, and INRAE, 2024.
Abstract
We provide a finite volume approximation in dimension d>1 to a quasilinear parabolic equation with discontinuous hysteresis modelling a phase change, arising as a singluar limit of a pseudo-parabolic regularisation of a foward-backward diffusion equation. The convergence of the numerical solution to a suitable weak entropy solutions is shown under a parallelism assumption between the nonlinearities driving the evolution in each phase. The main challenge lies in the treatment of the discontinuous hysteresis operator in the proof of the compactness of the sequence of approximate solutions. This is achieved by regularising the hysteresis operator with a continuous one for which Hilpert inequalities are accessible and let us obtain crucial uniform translation estimates in L1 in space. Numerical simulations, computed using a Julia-based framework for the finite volume discretisation of reaction-diffusion equations, are shown. -
B. García-Archilla, V. John, J. Novo, POD-ROMs for incompressible flows including snapshots of the temporal derivative of the full order solution, Preprint no. arXiv:2206.09123, Cornell University, 2022, DOI 10.48550/arXiv.2206.09123 .
-
V. John, X. Li, Ch. Merdon, H. Rui, Inf-sup stabilized Scott--Vogelius pairs on general simplicial grids by Raviart--Thomas enrichment, Preprint no. arXiv:2206.01242, Cornell University, 2022, DOI 10.48550/arXiv.2206.01242 .
-
M. Coghi, W. Dreyer, P. Gajewski, C. Guhlke, P. Friz, M. Maurelli, A McKean--Vlasov SDE and particle system with interaction from reflecting boundaries, Preprint no. 2102.12315v1, Cornell University Library, arXiv.org, 2021.
-
V. John, P. Knobloch, On algebraically stabilized schemes for convection-diffusion-reaction problems, Preprint no. 2111.08697, Cornell University Library, arXiv.org, 2021.
-
J. Fuhrmann, C. Guhlke, Ch. Merdon, A. Linke, R. Müller, Induced charge electroosmotic flow with finite ion size and solvation effects, Preprint no. arXiv:1901.06941, Cornell University Library, 2019, DOI 10.1016/j.electacta.2019.05.051 .
-
A. Linke, Ch. Merdon, M. Neilan, Pressure-robustness in quasi-optimal a priori estimates for the Stokes problem, Preprint no. arXiv:1906.03009, Cornell University Library, arXiv.org, 2019.
-
N. Alia, V. John, S. Ollila, Re-visiting the single-phase flow model for liquid steel ladle stirred by gas, Preprint no. arXiv.1811.11535, Cornell University Library, arXiv.org, 2018, DOI 10.1016/j.apm.2018.11.005 .
Abstract
Ladle stirring is an important step of the steelmaking process to homogenize the temperature and the chemical composition of the liquid steel and to remove inclusions before casting. Gas is injected from the bottom of the bath to induce a turbulent flow of the liquid steel. Multiphase modeling of ladle stirring can become computationally expensive, especially when used within optimal flow control problems. This paper focuses therefore on single-phase flow models. It aims at improving the existing models from the literature. Simulations in a 2d axial-symmetrical configuration, as well as, in a real 3d laboratory-scale ladle, are performed. The results obtained with the present model are in a relative good agreement with experimental data and suggest that it can be used as an efficient model in optimal flow control problems. -
N.R. Gauger, A. Linke, P. Schroeder, On high-order pressure-robust space discretisations, their advantages for incompressible high Reynolds number generalised Beltrami flows and beyond, Preprint no. arXiv:1808.10711, Cornell University Library, arXiv.org, 2018.
Abstract
Recently, high-order space discretisations were proposed for the numerical simulation of the incompressible Navier--Stokes equations at high Reynolds numbers, even for complicated domains from simulation practice. Although the overall spatial approximation order of the algorithms depends on the approximation quality of the boundary (often not better than third order), competitively accurate and efficient results were reported. In this contribution, first, a possible explanation for this somewhat surprising result is proposed: the velocity error of high-order space discretisations is more robust against quantitatively large and complicated pressure fields than low-order methods. Second, it is demonstrated that novel pressure-robust methods are significantly more accurate than comparable classical, non-pressure-robust space discretisations, whenever the quadratic, nonlinear convection term is a nontrivial gradient field like in certain generalised Beltrami flows at high Reynolds number. Then, pressure-robust methods even allow to halve the (formal) approximation order without compromising the accuracy. Third, classical high-order space discretisations are outperformed by pressure-robust methods whenever the boundary is not approximated with high-order accuracy. This improved accuracy of (low-order) pressure-robust mixed methods is explained in terms of a Helmholtz--Hodge projector, which cancels out the nonlinear convection term in any generalised Beltrami flow, since it is a gradient field. The numerical results are illustrated by a novel numerical analysis for pressure-robust and classical space discretisations. Further, the relevance of these results is discussed for flows that are not of Beltrami type.
Contact
Contributing Groups of WIAS
Projects/Grants
- Dynamic wetting and dewetting of viscous liquid droplets films on viscoelastic substrates
- Equilibria for Distributed Multi-Modal Energy Systems under Uncertainty
- Multicriteria optimization subject to equilibrium constraints using the example of gas markets
- Stochastic gradient methods for almost sure state constraints for optimal control of gas flow under uncertainty