Benedikt Jahnel
Mitarbeiterinnen und Mitarbeiter:
Jonas Köppl, Lukas Lüchtrath, Peteris Klavs Silins, Anh Duc Vu
Teamassistenz:
Christina van de Sand





Von links nach rechts: Benedikt Jahnel, Jonas Köppl, Lukas Lüchtrath, Christina van de Sand, Anh Duc Vu.
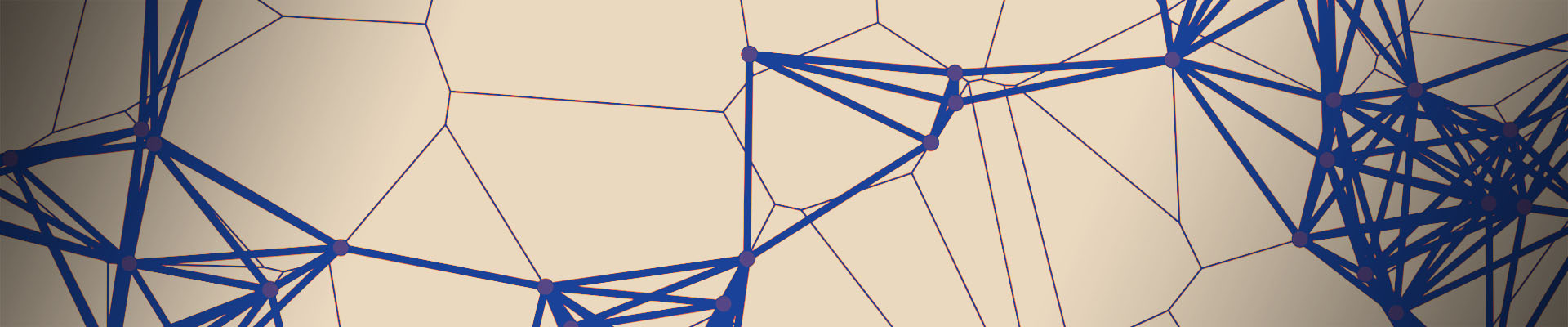
mit Basisstationen (grün) und mobilen Geräten
(blau). Über D2D-Verbindungen werden die
Abdeckungszonen (Grüntöne) der Basisstationen dynamisch erweitert.
- Verbesserung der Konnektivität in mobilen urbanen D2D-erweiterten Netzwerken
- Datenrouting in D2D-Systemen
- Verbreitung von Malware in reinen D2D-Systemen
- Dynamische Kontinuumsperkolation
- Theorie großer Abweichungen für Raum-Zeit-Punkt-Prozessen
- Interagierende Partikelsysteme auf Zufallsgraphen
In einer zunehmend vernetzten Welt mit dem Internet der Dinge (IoT), der Kommunikation von Gerät zu Gerät (D2D), selbstfahrenden Autos und interagierenden intelligenten Geräten muss eine überwältigende Datenmenge schnell über hochkomplexe Netzwerke übertragen werden. Die unvermeidlichen dramatischen Änderungen in der Systemarchitektur wirken sich auf fast jeden Aspekt des Netzwerkdesigns aus. Mit der Einführung des neuen 5G-Telekommunikationsstandards werden beispielsweise schnellere Verbindungen, höherer Durchsatz und mehr Kapazität über ein verbessertes mobiles Breitband ins Auge gefasst. Darüber hinaus sollte eine äußerst zuverlässige Kommunikation mit geringer Latenz das System in die Lage versetzen, zeitkritische Anwendungen wie die Kommunikation von Auto zu Auto zu unterstützen, während massive Kommunikationssysteme vom Maschinentyp den Schlüssel für einen erfolgreichen Übergang in Richtung Industrie 4.0 darstellen.
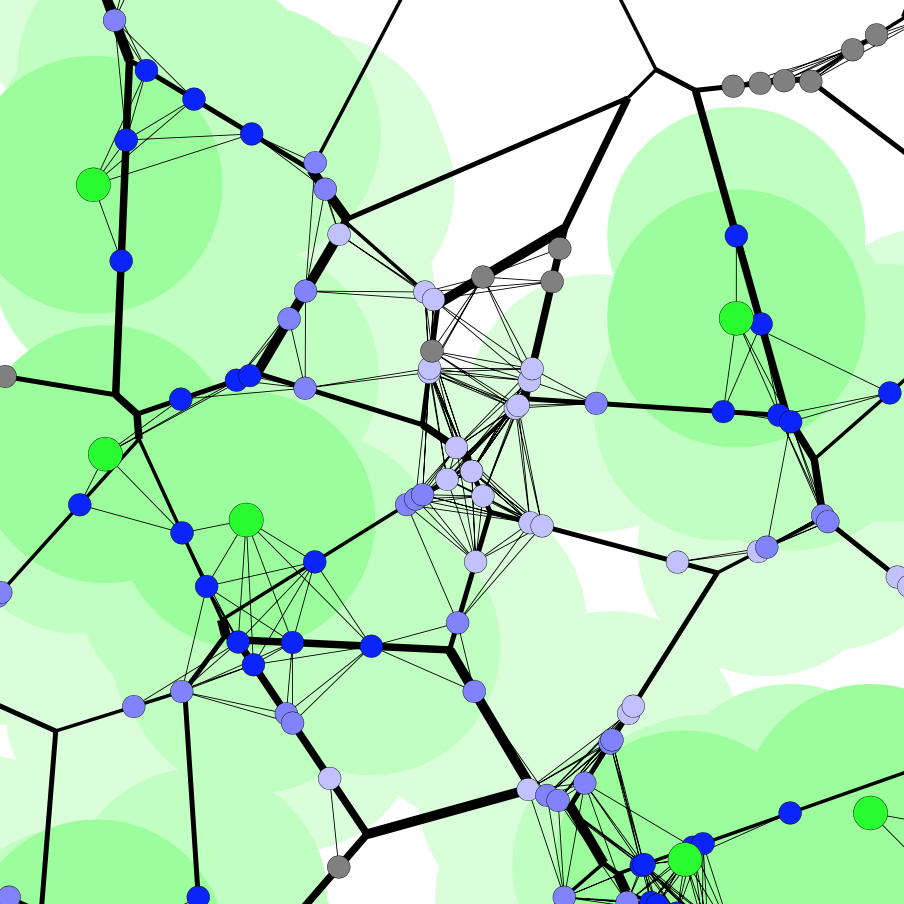
über ein gerichtetes Routing-Schema (schwarze
Ränder) an eine zentrale Basisstation (grün) senden.
Angesichts dieser ständig wachsenden Möglichkeiten, aber auch der Anforderungen moderner Kommunikationssysteme wird die D2D-Kommunikation (Device-to-Device) zu einer der Schlüsseltechnologien, die eine Vielzahl von Anwendungsfällen durchdringen, siehe beispielsweise die Proximity-Based Messenger Apps Firechat, Briar oder Bridgefy. Obwohl Sensornetzwerke und verwandte Ad-hoc-Netzwerke in der Wissenschaft theoretisch ausführlich diskutiert wurden, bilden die jüngsten technologischen Durchbrüche erst jetzt die Grundlage dafür, dass die D2D-Technologie ihr volles Potenzial entfalten kann. Die geplanten Vorteile sind vielfältig und reichen von Erweiterungserweiterungen in Schwellenländern über Robustheit der Netzwerke bis hin zu umweltfreundlichen Netzwerken in städtischen Umgebungen.
Gleichzeitig sind D2D-Komponenten für Netzwerkbetreiber weniger steuerbar und ihre Leistung schwankt stärker. Eine gründliche und sorgfältige Modellierung und Analyse ist daher entscheidend, um potenzielle Bedrohungen für die Servicequalität in solchen Netzwerken zu identifizieren und zu mindern. Hier haben sich Methoden der Wahrscheinlichkeitstheorie sowohl bei der Analyse als auch beim Design des Systems als hilfreich erwiesen. Es ist zu beachten, dass die Wahrscheinlichkeit auf zwei Arten ins Bild kommt: Es ist unabdingbar, mit intrinsischen Unsicherheiten im Netzwerk wie den Standorten von Geräten umzugehen, aber es ist auch äußerst hilfreich, da beispielsweise stochastische Algorithmen zur Verwaltung des Systems verwendet werden können.
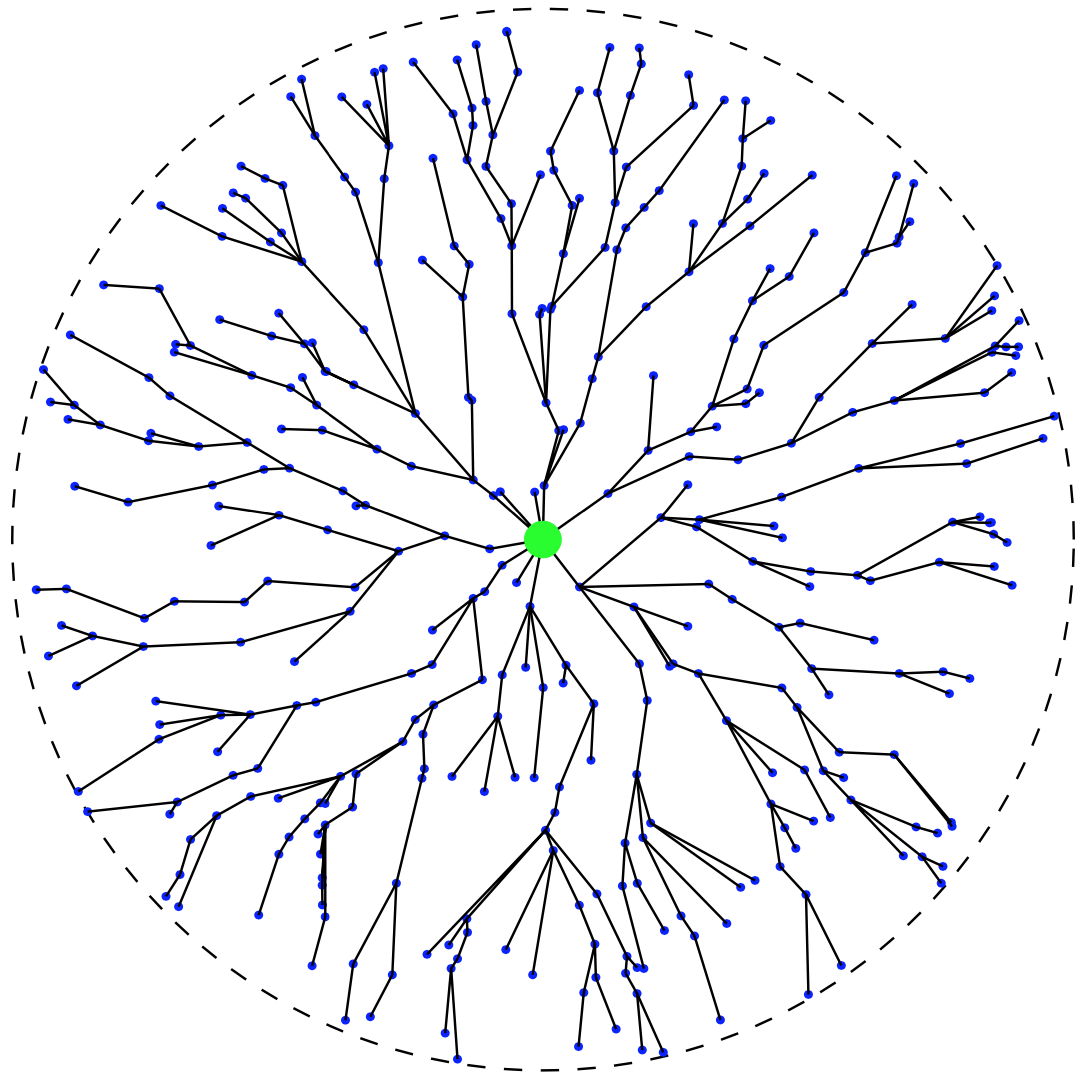
in einem D2D-Netzwerk anfälliger Knoten (blau)
mit weißen Rittern (grün), die Patches enthalten.
Der allgegenwärtige Ansatz für eine umfassende Modellierung mobiler D2D-Netzwerke besteht darin, die Netzwerkkomponenten als Punkte in einem stochastischen Punktprozess zu identifizieren. Das statistische Wissen über Benutzerverhalten, Umgebungsbedingungen oder Mobilität wird dann in der Verteilung der zufälligen Punktwolke codiert. Die Art und Weise, wie Nachrichten oder Datenpakete von Gerät zu Gerät übertragen werden, ist ein hochkomplizierter Mechanismus, der Codierungsschemata, Protokolle für den mittleren Zugriff, Interferenzkontrolle, Sicherheitsanforderungen, Routing-Schemata und viele weitere Aspekte umfasst. Typischerweise spiegelt sich diese Komplexität in zusätzlichen Ebenen zufälliger Eingaben wider, die in ein aussagekräftiges umfassendes Modell des dynamischen Systems integriert werden müssen. Letztendlich muss die Leistung des Netzwerks anhand einer Vielzahl von Leistungsmetriken bewertet werden, beispielsweise anhand des Durchsatzes, die an die spezifischen Anwendungsfälle angepasst sind und zu einer Vielzahl von empfohlenen Maßnahmen für Netzwerkbetreiber und -designer führen.
Der Stand der Technik auf dem Gebiet der probabilistischen Modellierung und strengen Analyse räumlicher D2D-Netzwerke konzentriert sich normalerweise auf isolierte Aspekte des soeben beschriebenen Gesamtbildes. Es speist sich aus einer Vielzahl von Communities, die von Ingenieurwesen, Physik, Computer- und Informationswissenschaft bis hin zu angewandter Mathematik reichen. Der Großteil der derzeit verfügbaren Arbeiten zu diesem Thema trägt zum Verständnis statischer Netzwerke bei, in denen Geräte unbeweglich und unabhängig voneinander zufällig verteilt sind, wobei der Schwerpunkt auf Konnektivität und Kapazität liegt, um das erwartete Verhalten zu verstehen. Hier wird die Leibniz Junior Research Group entscheidende Fortschritte machen. Wir möchten den Einfluss der Gerätemobilität in realistischen Umgebungen auf die Systemleistung verstehen und vorhersagen. Wir möchten verschiedene Routing- und Zugriffsstrategien zur Interferenzreduzierung in Mehrkanal-D2D-Kommunikationsnetzen analysieren und verstehen, wie sich erwünschte und unerwünschte Daten im System verteilen. Dazu müssen wir die Theorie der räumlichen stochastischen Dynamik, der Navigation und der abhängigen zufälligen Ausdünnung für Punktprozesse sowie der Markovschen und nicht-Markovschen Dynamik auf zufälligen Graphen weiterentwickeln, auch hinsichtlich ihres Verhaltens bei mathematischen großen Abweichungen.
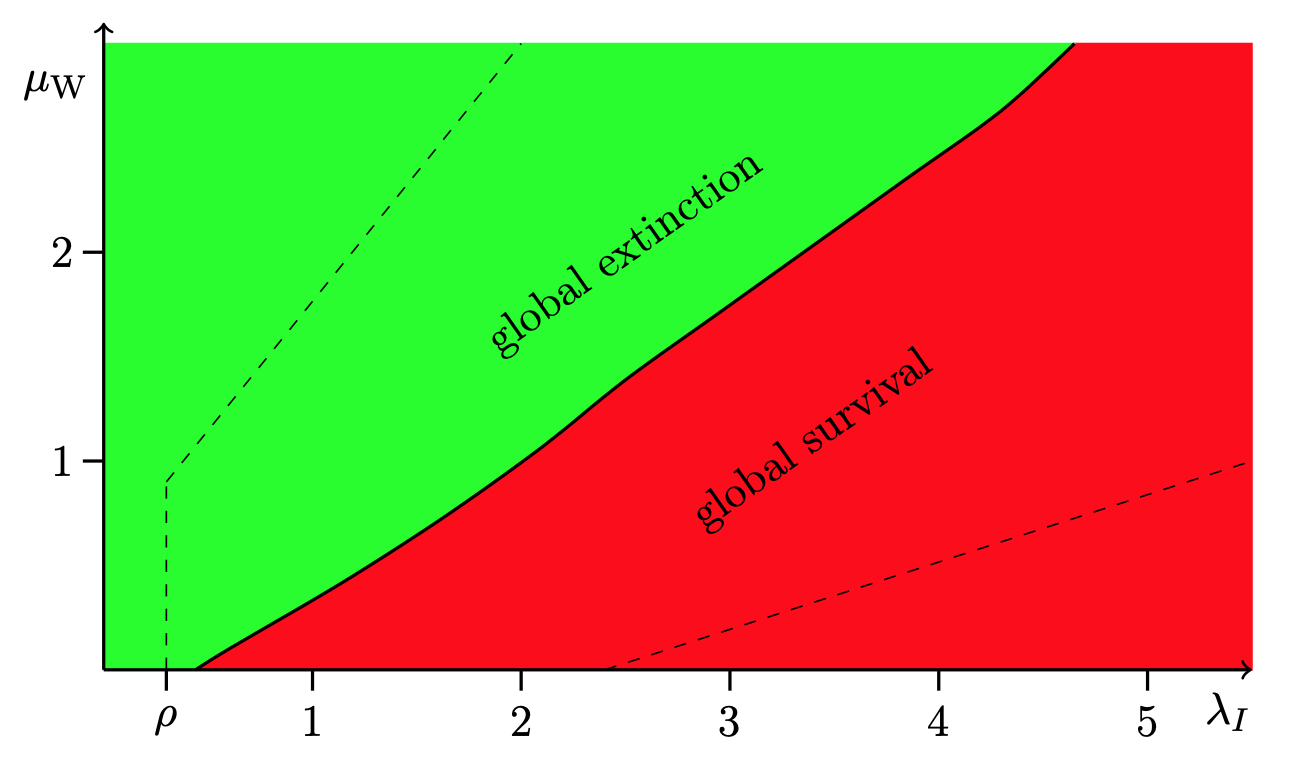
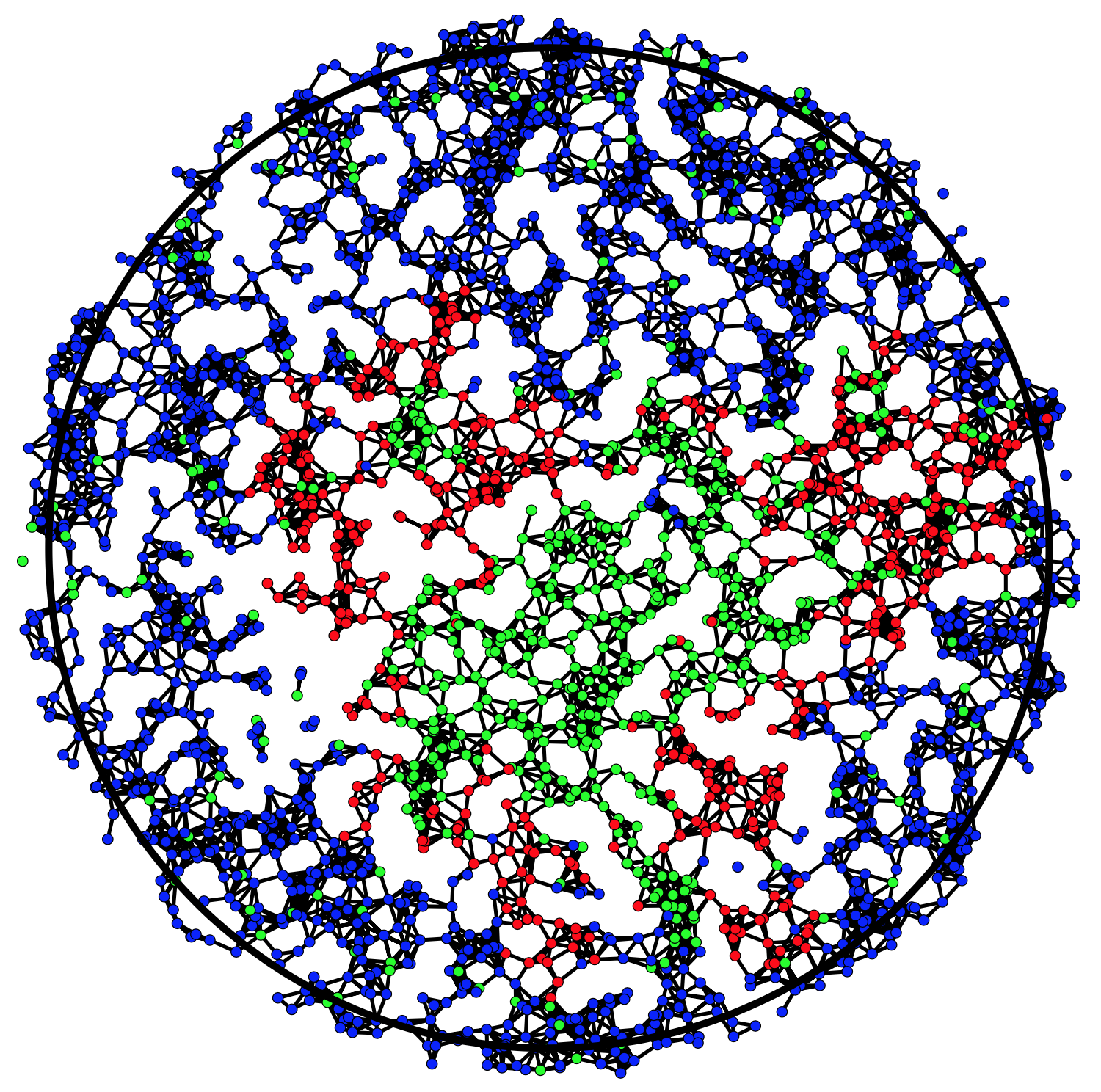
globalem überleben und Auslöschung eines
Virus in einem zufälligen Wachstumsmodell auf
dem Poisson-Gilbert-Graphen.
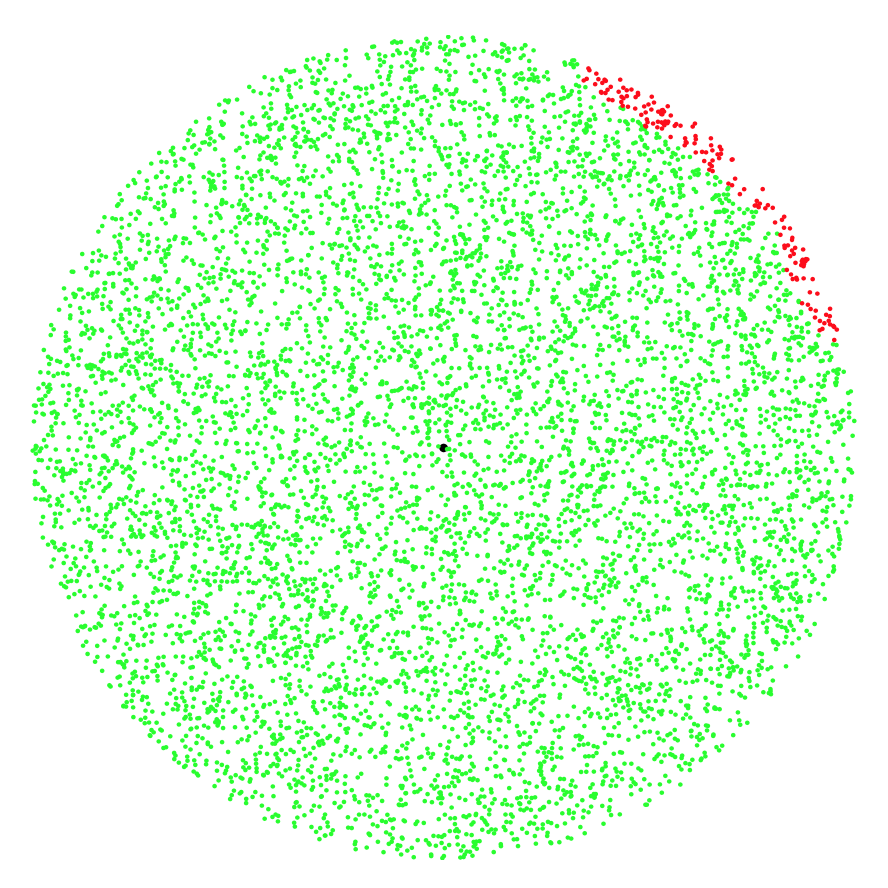
(grün, rot), die darauf abzielen, unter Interferenz-
bedingungen eine Verbindung zum Zentrum her-
zustellen. Rote Punkte werden aufgrund des großen
Abstands und der Interferenz, die durch
zu viele Punkte im Zentrum erzeugt wird, getrennt.

(blau) basierend auf einem Cox-Punkt-Prozess
(rot) mit zufälliger Umgebung (grün), gegeben
durch ein unabhängiges Poisson-Boolesches Modell.
Flexible Forschungsplattform
- Datengetriebene Optimierung und Steuerung
- Erhaltungssätze und Bilanzgleichungen für Multikomponentensysteme
- Numerische Methoden für innovative Halbleiter-Bauteile
- Probabilistische Methoden für dynamische Kommunikationsnetzwerke
- Simulation von Halbleiterbauelementen für Quantentechnologien
- Ehemalige Gruppen