Numerische Methoden für innovative Halbleiter-Bauteile

Leitung:
Patricio Farrell

Mitarbeiterinnen und Mitarbeiter:
Dilara Abdel, Zeina Amer, Yiannis Hadjimichael

Teamassistenz:
Imke Weitkamp

von links nach rechts: Patricio Farrell, Dilara Abdel, Zeina Amer, Yiannis Hadjimichael, Imke Weitkamp

Überblick

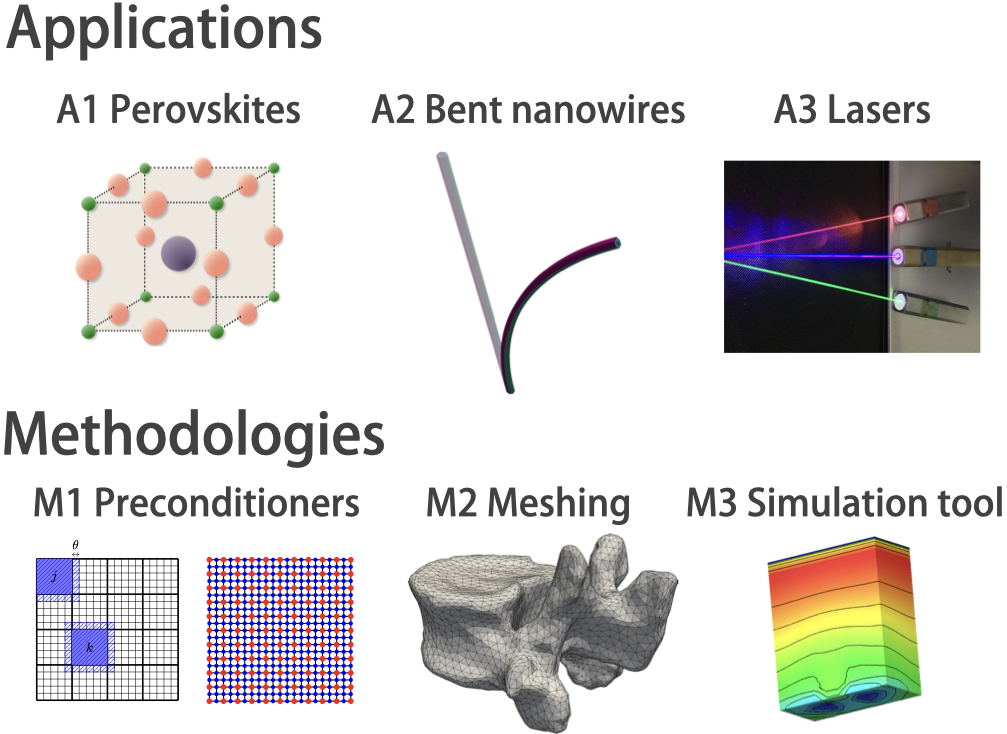
Die Leibniz-Gruppe NUMSEMIC entwickelt und löst nichtlineare PDE-Modelle. Diese Modelle sind häufig durch Ladungstransport in innovativen Halbleiterbauelementen inspiriert. Zu den Anwendungen gehören insbesondere Perowskit-Solarzellen, Nanodrähte, Laser sowie die Dotierungsrekonstruktion. Um diese Anwendungen in mathematische Modelle zu übersetzen, stützen wir uns auf nichtlineare Drift-Diffusions-Gleichungen, hyperelastische Materialmodelle, inverse PDE-Probleme, lokalisierte Landschaftstheorie und atomistische Kopplung. Unsere Methodiken umfassen physikerhaltende Finite-Volumen-Methoden, datengesteuerte Techniken sowie gitterfreie Methoden.

Forschungsschwerpunkte

• Modellieren mit und numerische Lösen von Systemen nichtlinearer partieller Differentialgleichungen
• Nichtlineare Drift-Diffusionsmodelle, hyperelastische Materialien, inverse PDE-Probleme, lokalisierte Landschaftstheorie und atomistische Kopplung
• Physik-erhaltende Finite-Volumen-Methoden auf Voronoi-Gittern
• Ladungstransport in Halbleitern/Bauteilen
• Präkonditionierer und anisotrope Gitter-Strategien
• Hochdimensionale gitterfreie Approximation
• Datengetriebene Techniken für schlecht gestellte inverse Probleme

Ausführlichere Informationen finden sich auf der englischsprachigen Version dieser Webseite.

Highlights

Siehe die englischsprachige Version dieser Webseite.