WIAS Research Highlights 2021 and 2022
back to recent research highlights »
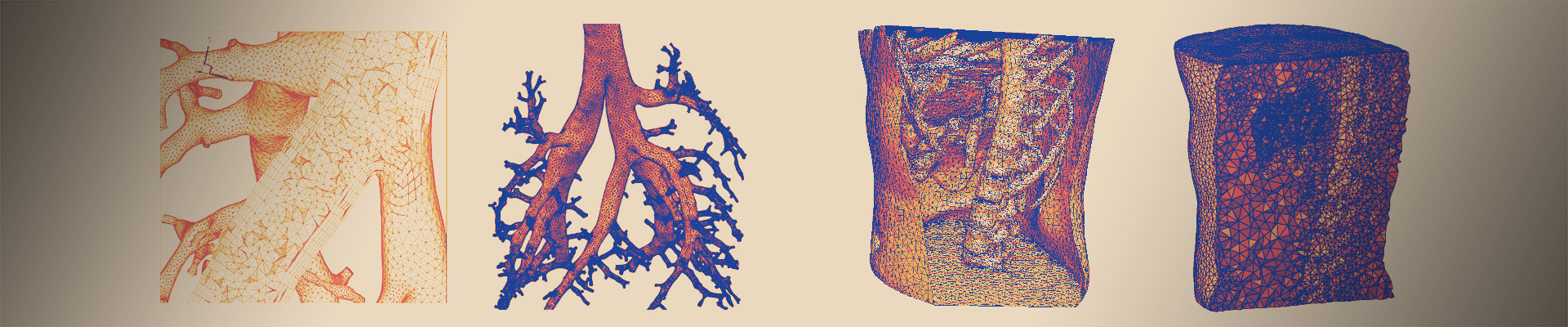
Biophysics-based Modeling and Simulation in Medical Imaging
A. Caiazzo, S. Katz, and K. TabelowModern image acquisition technologies allow clinicians to record detailed information not only on patient anatomy, but also related to biophysical processes. We focus on three selected applications of mathematical methods in this context.
Energy-based Solution Concepts for a Geophysical Fluid Model
T. Eiter, and R. LasarzikOn a model that describes the deformation of rocks in the lithosphere as the flow of a fluid with viscous, elastic, and plastic properties is studied and a generalized solution concept is proposed.
Extremely Short Optical Pulses
S. AmiranashvilUltrashort optical pulses are of great theoretical and practical interest. Practical applications of these pulses clearly benefit from the reduction in pulse duration, which enhances data transmission capacity and enable the observation of extremely fast processes.
How do Ants Form Trails?
R.I.A. PattersonWe identify simple mathematical models that explain how active particles or agents can interact with each other to form large-scale structures and patterns (like models that are appropriate on the time and space scales of insects such as ants).
Hydrogels Models for Soft Biomaterials
A. H. Erhardt, D. Peschka, L. Schmeller, and B. WagnerA journey from a novel abstract thermodynamic description, to nonlinear coupled systems that capture the various phase transitions in hydrogels, to agent models for cell motion in these materials.
Model-based Geometry Reconstruction of Quantum Dots from TEM
A. Maltsi, T. Koprucki, K. Tabelow, and T. StreckenbachWe explore the structure and composition of materials such as semiconductor quantum dots and discover how mathematical theory plays a critical role in solving the reconstruction problem and automated processing of transmission electron microscopy (TEM) images.
Multi-scale Chemical Reaction Systems
A. StephanThinking of everyday biochemical processes, chemical reaction systems are intrinsically of multi-scale nature, which involves many challenging difficulties. We show, how, in a thermodynamical consistent way, the complexity can be reduced by deriving effective gradient systems.
Optimization and Uniform Point Sets on the Sphere
H. Heitsch, and R. HenrionWe provide a fully explicit, easy to implement formula for the spherical cap discrepancy - a widely used measure for how uniformly a sample of points on the sphere is distributed.
Perovskite Models, Finite Volume Methods, and Painless Simulation
D. Abdel, P. Farrell, J. Fuhrmann, and P. VagnerPerovskite solar cells are an efficient alternative to classical silicon ones. We deal with the question how their efficiency can be further improve while preventing degradation in four stages: modeling, discretization, analysis, and simulation.
Probabilistic Methods for Communication Systems
A. Hinsen, and B. JahnelThe explosion of interconnected devices requires radical advancements in the design of communication networks including for example peer-to-peer data transmission. Probabilistic methods can help to analyze the potential benefits but also challenges of such systems.
RKHS Regularization of Singular Local Stochastic Volatility McKean-Vlasov Models
C. Bayer, O. Butkovsky, and J. SchoenmakersOn a novel regularization method for the problem of calibrating local stochastic volatility models. Numerical results suggest that the approach is efficient for the calibration of local stochastic volatility models and can outperform widely used local kernel methods.
Quasi-Variational Inequalities and Optimal Control
A. Alphonse, and M. HintermüllerQuasi-variational inequalities (QVIs) are powerful mathematical objects that can be used to describe real-world phenomena as varied as thermoforming, or fluid flow in the heart. The control of QVIs is important from the point of view of theoretical understanding as well as for applications.