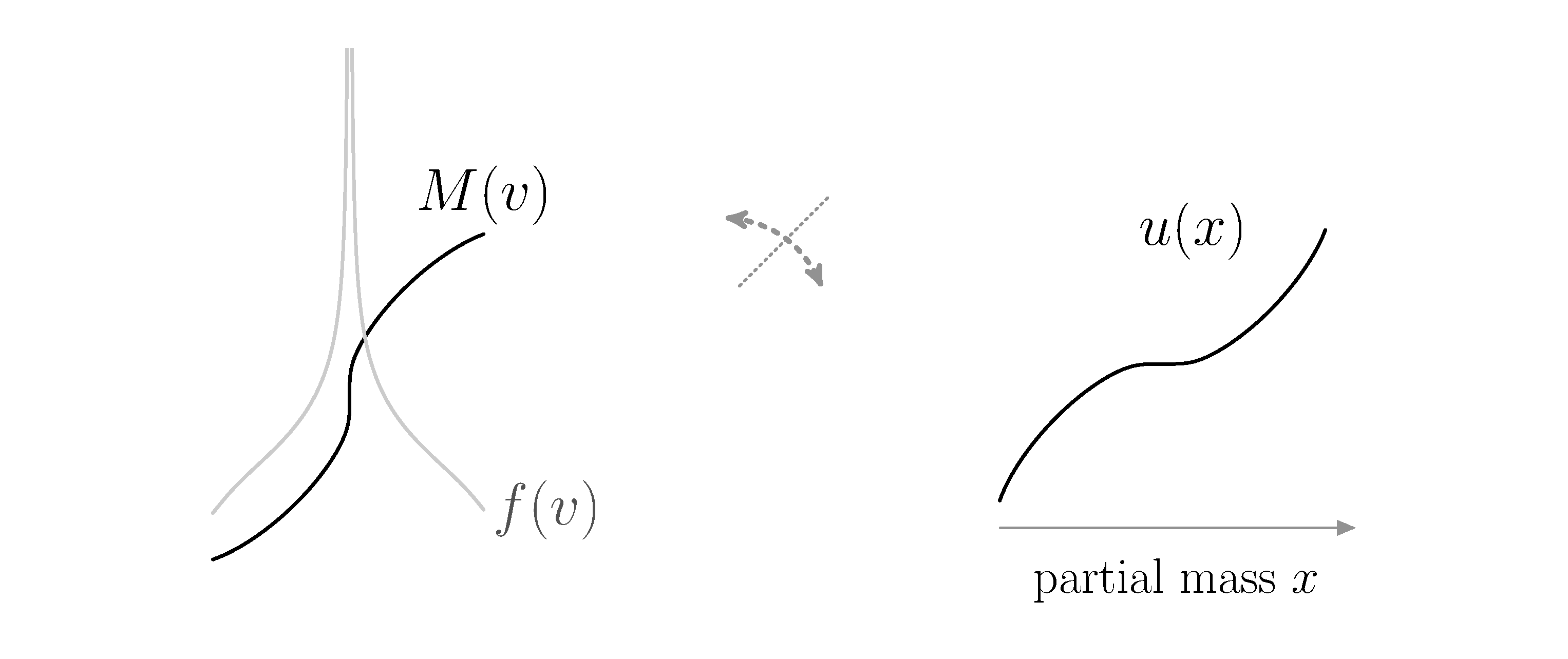Dissertation von Katharina Hopf mit Faculty of Science Thesis Prize in Mathematics der Universität Warwick ausgezeichnet
In den frühen 1990er Jahren führten Kaniadakis und Quarati eine Klasse von Fokker-Planck-Gleichungen mit quadratischem Drift als Kontinuumsmodelle für das Langzeitverhalten eines homogenen Quantensystems identischer und ununterscheidbarer Teilchen ein. Lösungen solcher Gleichungen können als Dichten verstanden werden, die bei gegebener Temperatur zu festem Zeitpunkt die Geschwindigkeitsverteilung des homogenen Systems beschreiben. Diese Gleichungen haben eine Familie von zeitunabhängigen glatten Lösungen, die im Folgenden als stationäre Zustände bezeichnet werden. Für Fermionen stimmen sie mit den klassischen Fermi-Dirac-Verteilungen und für Bosonen mit den Bose-Einstein-Verteilungen überein. Im Falle von Fermionen existiert für eine gegebene Temperatur genau ein stationärer Zustand, und es kann gezeigt werden, dass sich Lösungen im Langzeitlimes diesem Gleichgewichtszustand nähern. Für Bosonen in einem dreidimensionalen Geschwindigkeitsraum hingegen existiert eine kritische Temperatur, unterhalb derer sich kein regulärer stationärer Zustand mehr findet. Auf den ersten Blick ist daher unklar, wie sich Lösungen in diesem Fall typischerweise für große Zeiten verhalten sollten und ob sich diese schließlich in einer Art Gleichgewicht einpendelt. Einer der Hauptteile der vorliegenden Arbeit behandelt genau diese Frage.
Ein Kandidat für das potentielle Langzeitverhalten kann mit Hilfe der dem Problem zugrunde liegenden Entropie gefunden werden. In der Tat gibt es auch im Fall von Bosonen bei gegebener Temperatur genau einen Zustand, der das Entropiefunktional minimiert. Oberhalb der kritischen Temperaturschwelle stimmt dieser Zustand mit dem glatten stationären Zustand des Problems überein. Unterhalb der kritischen Schwelle ist er jedoch keine Funktion mehr, sondern ein Maß auf dem Geschwindigkeitsraum mit einer singulären Komponente, die bei Geschwindigkeit Null konzentriert ist (d.h. ein Dirac-Delta bei Null). Im Zusammenhang mit bosonischen Quantensystemen ist ein solches singuläres Maß physikalisch sinnvoll und wird als ein Bose-Einstein-Kondensat interpretiert.
Für ein Analogon in 1D des Modells von Kaniadakis und Quarati entwickelt die Arbeit einen Rahmen, um die Frage nach dem Langzeitverhalten rigoros zu beantworten. Eine grundsätzliche Schwierigkeit liegt dabei in dem Umstand, dass die ursprüngliche Formulierung der Gleichung nur für hinreichend reguläre Dichten sinnvoll ist. Insbesondere sind Maße mit einem singulären Anteil nicht zulässig.
Der Ansatz zur Lösung dieses Problems beruht auf einer Umformulierung des Problems zu einer Gleichung für die pseudo-inverse kumulative Verteilungsfunktion (siehe Abbildung unten), welche es erlaubt, die singulären Entropieminimierer als Lösungen im Viskositätssinn zu begreifen. Basierend auf diesem Lösungskonzept lässt sich nun globale Wohlgestelltheit zeigen. Ein essentielles Werkzeug bildet dabei ein recht wirkmächtiges Vergleichsprinzip. Neben dem asymptotischen Verhalten für lange Zeiten erlaubt dieser Rahmen auch eine Untersuchung der qualitativen Eigenschaften von Lösungen wie etwa die blow-up Dynamik sowie die Formation und das mögliche Verschwinden von Kondensaten.