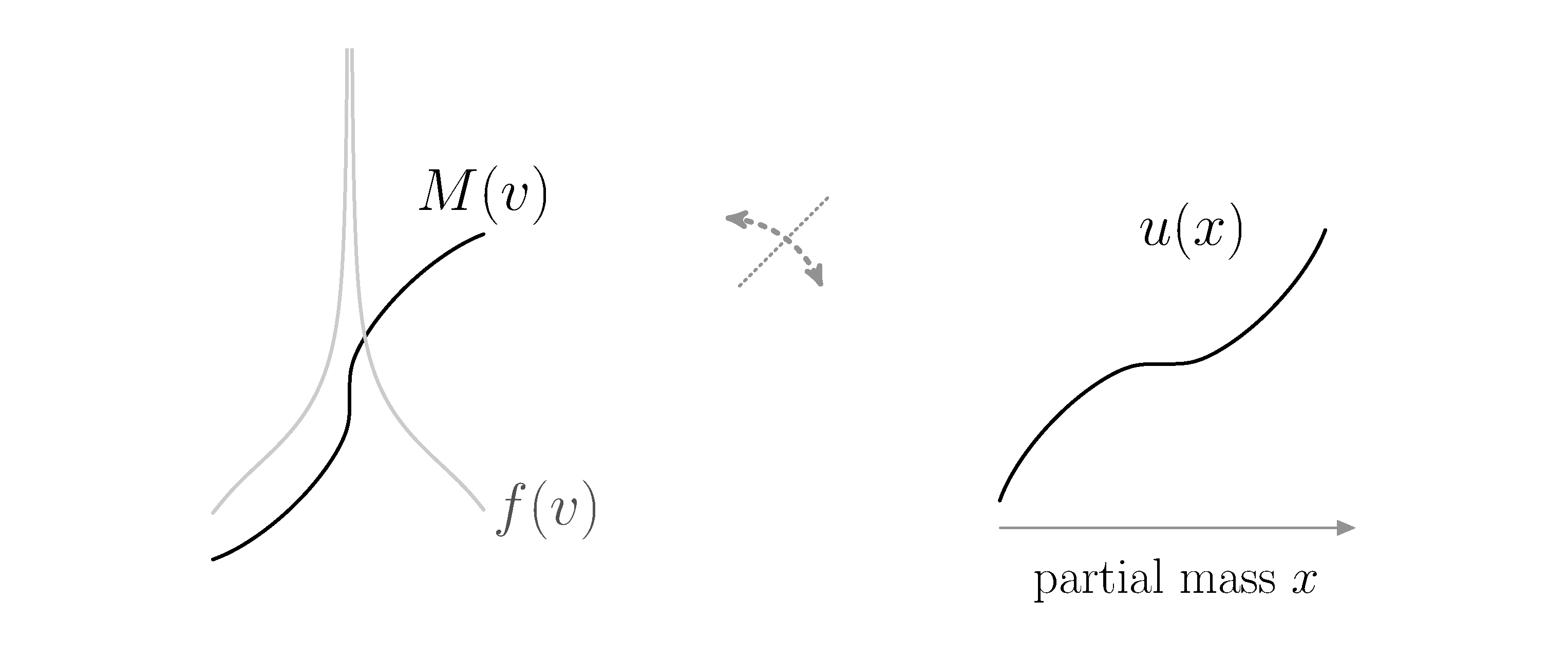Katharina Hopf's PhD thesis awarded Faculty of Science Thesis Prize in Mathematics at the University of Warwick
In the early 1990s, Kaniadakis and Quarati introduced a class of Fokker-Planck equations with quadratic drift as continuum models for the long-time dynamics of a spatially homogeneous system of identical and indistinguishable quantum particles. Solutions of such equations should be thought of as densities describing for a given temperature, at each point in time, the distribution in velocity space of the homogeneous quantum system. These equations have a family of time-independent smooth solutions, referred to below as steady states. For fermions they coincide with the classical Fermi-Dirac distributions, and for bosons with the Bose-Einstein distributions. In the case of fermionic particles, for any given temperature, there exists exactly one steady state, and it can be shown that in the long-time limit, solutions approach this equilibrium state. For bosonic particles in a three dimensional velocity space, however, there exists a critical temperature, below which no regular steady state exists. At first glance, it is therefore unclear how in this case a solution should typically behave for long times and whether it eventually settles to some kind of equilibrium. One of the main parts of this thesis is centred around precisely this question.
Heuristics for the potential long-time behaviour can be obtained from an underlying convex entropy associated with the problem. In fact, also in the bosonic case, for a given temperature (even below the critical threshold) there exists precisely one state minimising the entropy functional. Above the critical temperature threshold this state coincides with the smooth steady state of the problem. Below the critical threshold, however, it is no longer a function, but rather a measure on the velocity space with a singular component concentrated at velocity zero (i.e. a Dirac delta at zero). In the context of bosonic quantum systems, such a singular measure is physically meaningful and interpreted as a Bose-Einstein condensate.
For a 1D analogue of the model by Kaniadakis and Quarati, the thesis establishes a framework to answer rigorously the question of the long-time asymptotic behaviour and proves that in this setting solutions indeed relax to the unique measure minimising the entropy. Here, a fundamental difficulty lies in the fact that the original formulation of the equation is only meaningful for sufficiently regular densities. In particular, measures with a singular part are not admitted when using standard weak formulations of the PDE, and possible renormalised forms (which can make sense of the entropy minimisers) appear to be too weak a concept for ensuring wellposedness of the problem, since uniqueness may not be expected.
The approach to cope with this issue takes a mass transportation perspective and is based on a reformulation of the problem in terms of the pseudo-inverse distribution function (see the figure below). While the equation in these new variables is highly nonlinear and degenerate, it allows to give a meaning to the singular entropy minimisers as solutions in the viscosity sense. Based on this notion of solution, a global-in-time wellposedness theory is developed. Here, a core ingredient is a rather powerful comparison principle, which is derived using maximum principles for semicontinuous functions. Besides the long-time asymptotics, the framework further allows to study the qualitative properties of solutions such as blow-up dynamics as well as formation and possible extinction of condensates.