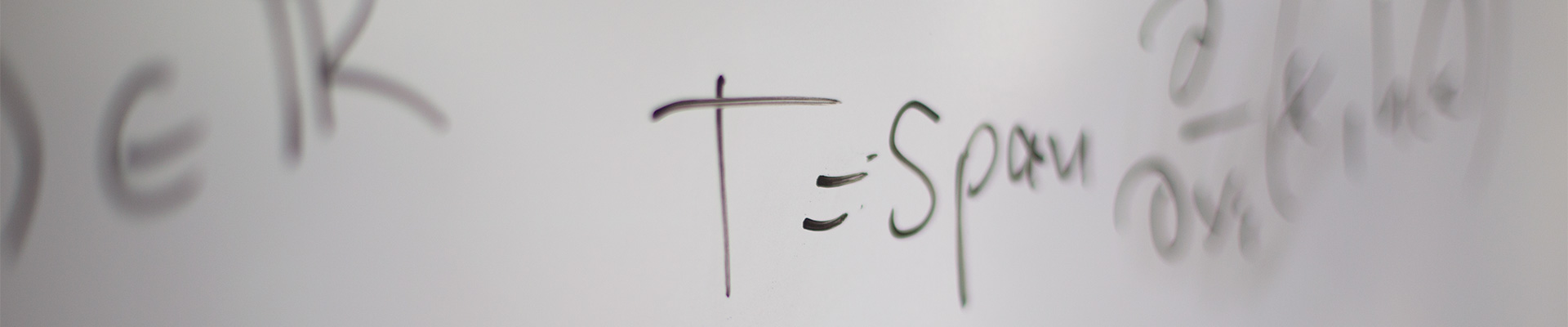Error estimates for the finite-element approximation of an elliptic control problem with pointwise state and control constraints
Authors
- Meyer, Christian
2010 Mathematics Subject Classification
- 49K20 49M25 65N30
Keywords
- Linear-quadratic optimal control problems, elliptic equations, state constraints, numerical approximation
DOI
Abstract
We consider a linear-quadratic elliptic optimal control problem with pointwise state constraints. The problem is fully discretized using linear ansatz functions for state and control. Based on a Slater-type argument, we investigate the approximation behavior for mesh size tending to zero. The obtained convergence order for the $L^2$-error of the control and for $H^1$-error of the state amounts $1-ve$ in the two-dimensional case and $1/2-ve$ in three dimension. In a second step, a state-constrained problem with additional control constraints is considered. Here, the control is discretized by constant ansatz functions. It is shown that the convergence theory can be adapted to this case yielding the same order of convergence. The theoretical findings are confirmed by numerical examples.
Download Documents