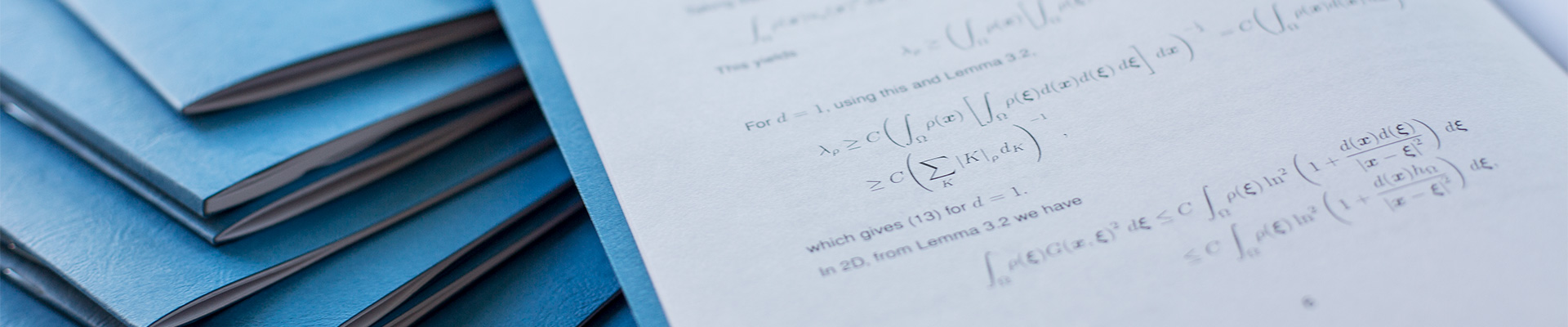Error analysis of the SUPG finite element discretization of evolutionary convection-diffusion-reaction equations
Authors
- John, Volker
ORCID: 0000-0002-2711-4409 - Novo, Julia
ORCID: 0000-0001-6667-5666
2010 Mathematics Subject Classification
- 65M12 65M60
Keywords
- Evolutionary convection-diffusion-reaction equation, Streamline-Upwind Petrov-Galerkin (SUPG) finite element method, backward Euler scheme, error analysis, time-continuous problem
DOI
Abstract
Conditions on the stabilization parameters are explored for different approaches in deriving error estimates for the SUPG finite element stabilization of time-dependent convection-diffusion-reaction equations that is combined with the backward Euler method. Standard energy arguments lead to estimates for stabilization parameters that depend on the length of the time step. The stabilization vanishes in the time-continuous limit. However, based on numerical experiences, this seems not to be the correct behavior. For this reason, the time-continuous case is analyzed under certain conditions on the coefficients of the equation and the finite element method. An error estimate with the standard order of convergence is derived for stabilization parameters of the same form that is optimal for the steady-state problem. Numerical studies support the analytical results.
Appeared in
- SIAM J. Numer. Anal., (2011) pp. 1149 -- 1176.
Download Documents