Development of an Ion-Channel Model-Framework for in-vitro assisted interpretation of current voltage relations
Project heads : Manuel Landstorfer, Jürgen Fuhrmann, Barbara Wagner
Cooperation partner: Robert S. Eisenberg (Rush Univ. Chicago)
Project staff : Christine Keller
MATH+ link :https://mathplus.de/research-2/application-areas/aa1-life-sciences/aa1-14/
Summary
Within this project a PDE based model framework was developed to better understand how ion channels control the flow of charged particles such as sodium and potassium in and out of cells. These channels are crucial for many life processes, from nerve signaling to muscle contraction. The new model combines physics, electrochemistry and mathematics to explain how these channels selectively allow certain ions to pass through and block others. By including detailed effects such as the size of the ions and interactions with water, the model provides a clearer picture of how these microscopic gatekeepers work.
Description
Ion channels are pore-forming proteins in cell membranes and like valves and transistors, they can be interpreted as “devices’’ which allow to control macroscopic system behavior with small energetical input. The behavior of such nanopores, even single ion channels, can be studied in laboratory conditions by measuring the current response to some time dependent voltage difference. This signal is a unique signature of a channel and its environment and depends on various local and global quantities.
The interpretation of measured current voltage (IV) relations, and especially their variation with the structure of the channel protein and bulk ion concentrations is of great importance for biology, physiology and medicine.
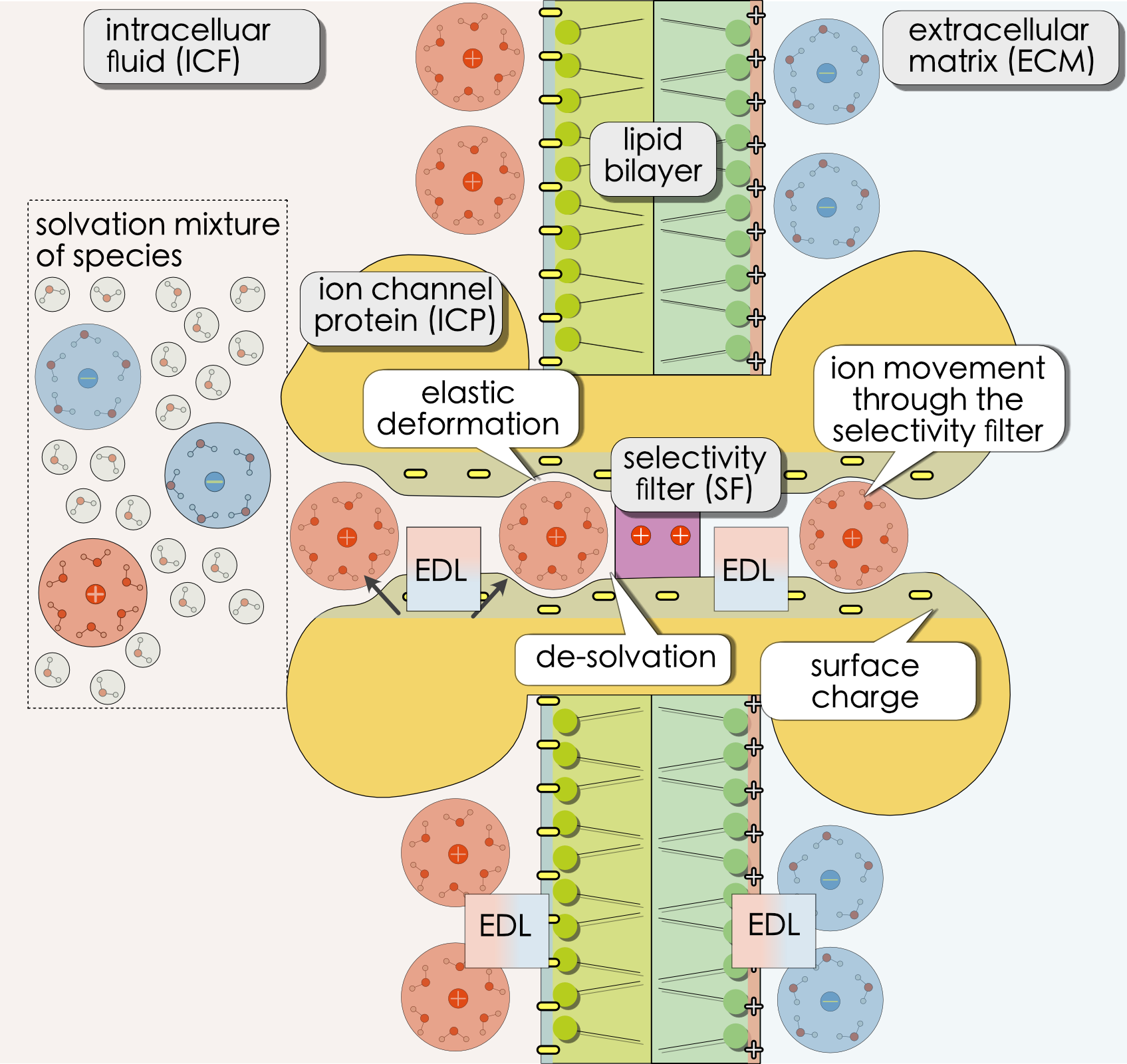
Sketch of a deformable ion channel modeled as a multidomain heterostructure.
Theoretical investigations of ion channels use methods from quantum chemical approaches via molecular dynamics (MD) simulations to PDE based models. While MD simulations resolve an ion channel on the atomic scale, enabling detailed investigations of the channel protein, they lack predictability on IV relations and bulk concentration variations, e.g. of Ca2+ concentrations from \(10^{-8}\) to \(10^{-6}\) M.
Continuum based, molecular mean field theories essentially yield averages of trajectories of MD simulations [1]. They treat the ion channel as a geometric domain without resolving all its atoms explicitly in space and allow to yield IV curves via numerical simulations. The project aims at the development of a continuum based mathematical and numerical modeling framework from first principles of non-equilibrium thermodynamics.
Methods
Based on the general field theory of coupled non-equilibrium thermo-electrodynamics [2], a continuum model for ion transport proteins in lipid bilayers was derived [3]. It incorporates a continuum model for electrolyte mixtures [4]–[6], which is developed at WIAS. The free energy density is a key factor of the modeling approach, which allows to account for solvation and finite ion size effects and to derive flow relations that govern non-equilibrium processes, e.g. diffusion along electrochemical gradients or electrochemical reactions at interfaces.The framework allows to consistently consider different compartments with different structures, e.g., liquid or solid electrolytes. This also required the derivation of nonlinear boundary conditions at interfaces.
In the scope of this project we consider a membrane including a single ion channel that is placed between two infinite resevoirs with an incompressible idealized mixture of sodium, calcium, chloride and water. Within the channel we consider a selectivity filter, an additional embedded domain that behaves like a solid or polymeric electrolyte. Hence, the free energy within the bulk regions and the selecivity filter is different. In the liquid electrolyte, the mixing entropy is determined by a mixture of freely moving ions and solvents, whereas in the polymeric electrolyte, immobile lattice-forming species such as amino acid residues of the channel protein and mobile ions passing through the channel mix. Furthermore, the ions diffuse more slowly through the solid region. In order to couple the different subdomains we derived interface reactions in terms of dehydration reactions. Throughout this work we treat the channel protein as a fixed boundary and assume that also the lattice sites are fixed.
The model is solved numerically in Julia using the VoronoiFVM.jl
package [7]. The Voronoi
Finite Volume Method is thermodynamically consistent as well as
positivity preserving, and mass conserving [8].
We are able to calculate current-voltage relations under different
conditions such as varying channel properties and ion
concentrations.
Results
The simulation results were validated with experimental current-voltage curves taken from literature for calcium selective ion channels [9]. Within the experiment the total ionic current for different extracellular calcium concentrations was measured. It was observed, that for low calcium concentrations a sodium current was measured. However, as the calcium concentration was increased, sodium was blocked and the calcium current was dominant. The model shows a good agreement with the experimental data and is able to depict this behavior which is known as anomalous mole fraction effect [3]. We used the diffusion coefficients within the selecitivity filter region to fit the model to the data. A comprehensive parameter study showed that the ionic currents not only depend on diffusion coefficients but also on the surface charge of the protein and the available space. More importantly, it is not clear in steady state experiments whether the ion flux through the channel is dominated due to diffusion or limited by the interface reactions.
During the project duration, further efforts on the numerical analysis of the finite volume method have been made. An earlier developed analogon of the Scharfetter-Gummel scheme nonlinear drift-diffusion problems defines its two-point numerical flux via an integral equation. A new approximation of this locally exact numerical flux has been introduced and investigated for its thermodynamic and convergence properties [10], [11]. It gives rise to possible future improvements of the discretization approach for the coupled systems.
Figure 1 shows a comparison of the total ion current calculated from the simulation (circles) with the total current measured experimentally (squares) [3]. We find that the model agrees with the data. The external calcium concentration is given in pCa = −log10([CaCl2]\(_{\text{out}}\)). By additionally plotting the partial sodium current (\(I_{Na^+}\), blue line) and the calcium current (\(I_{Ca^{2+}}\), red-orange line), it can be seen that at low pCa, mainly a sodium current is measured. We therefore conclude that the channel is blocked for monovalent cations at a certain extracellular Ca2+ concentration and that the current is then dominated by the Ca2+ current. This behavior is also known as the anomalous molar fraction effect (AMFE).
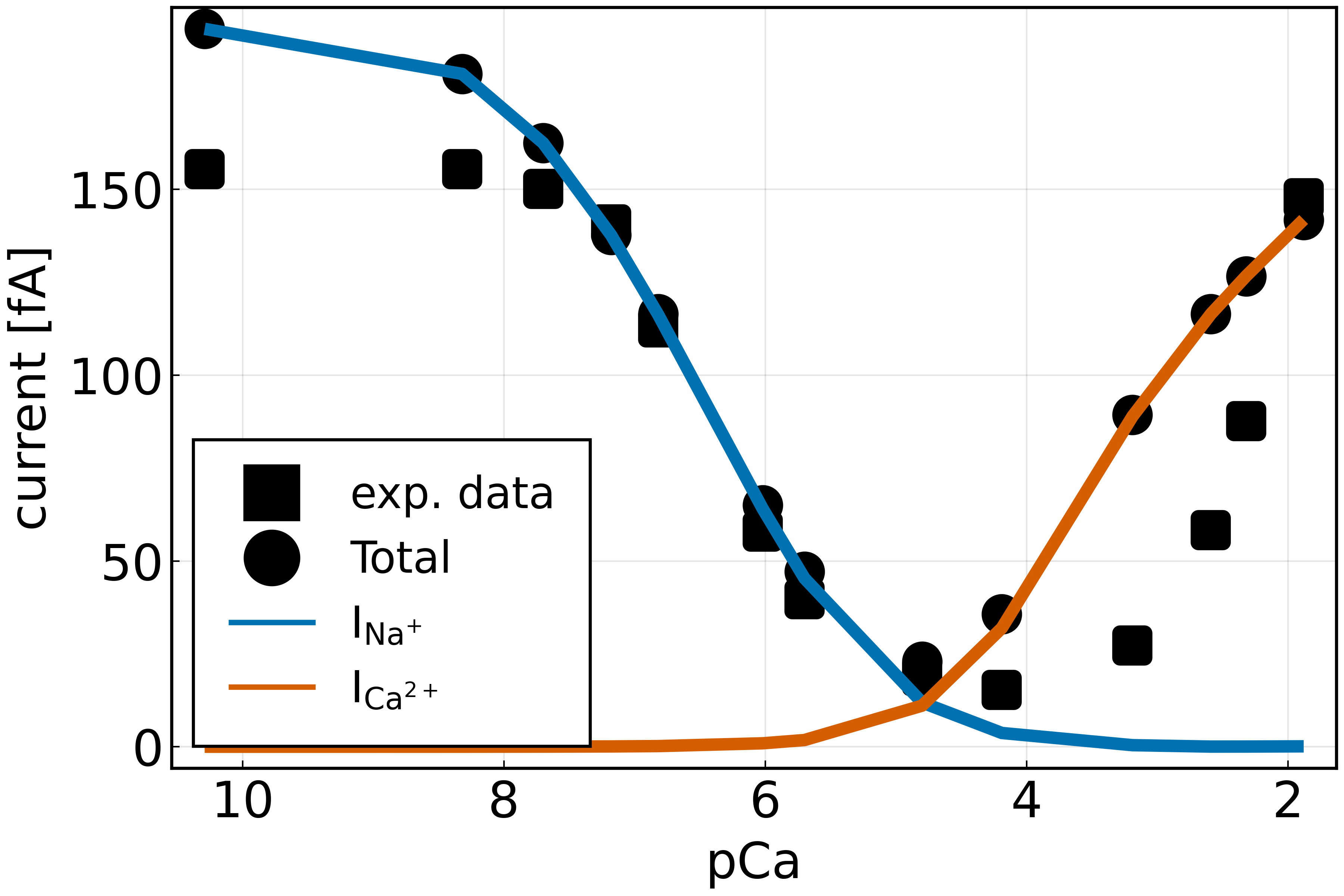
Figure 1. Total current for different calcium concentrations in the outer bath. Model simulation (circles) compared to experimental data (squares) from Almers et al. Figure 11A [9].
Figure 2 (a) illustrates the total current (black), the sodium current (blue) and calcium current (red-orange) as a function of an applied surface charge on the channel wall [3]. We can observe that as the surface charge increases, the calcium current rises continuously, while the sodium current initially increases, reaches a maximum, and then decreases again.
Figure 2 (b) shows the currents as a function of the number of lattice sites that are available in the selectivity filter (see [3] for more details). As the number of lattice sites increases we find that the calcium current decreases while the sodium current increases.
The results illustrated in Figure 2 indicate that space-charge competition might play an important role in the selectivity of monovalent over bivalent ions in channels and in the AMFE.
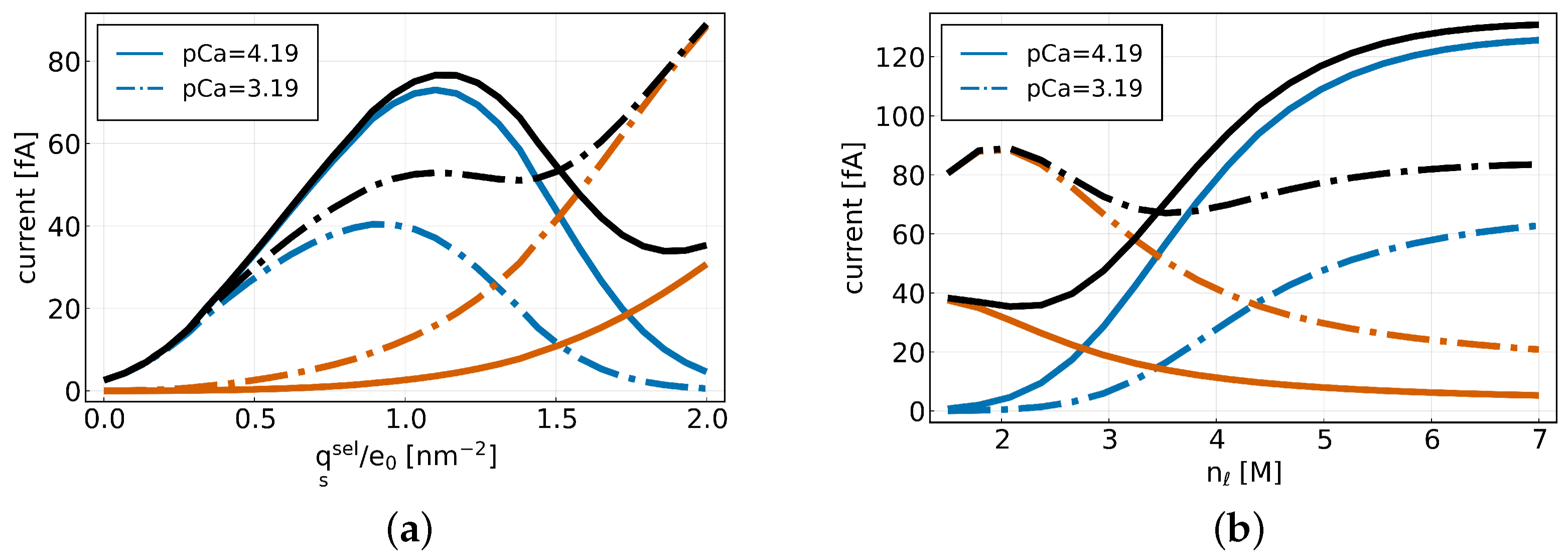
Figure 2. (a) Sodium (blue), calcium (red-orange), and total (black) currents plotted as a function of the surface charge for different calcium concentrations pCa = 4.19 (solid) and pCa = 3.19 (dash). (b) Sodium (blue), calcium (red-orange) and total (black) currents plotted as a function of the number of lattice sites for different calcium concentrations.