Numerical Mathematics and Scientific Computing

The group contributes to the following mathematical research topics of WIAS:

A main research field is the development, analysis, improvement and application of numerical methods for equations coming from CFD. The spatial discretization of the equations is based on finite element and finite volume methods. A focus of research is on so-called physically consistent methods, i.e., methods where important physical properties of the continuous problem are transferred to the discrete problem. [>> more]

The mathematical modelling of many scientific and technological problems leads to (initial) boundary value problems with systems of partial differential equations (PDEs). [>> more]

Archive

Further mathematical research topics where the institute has expertise in:

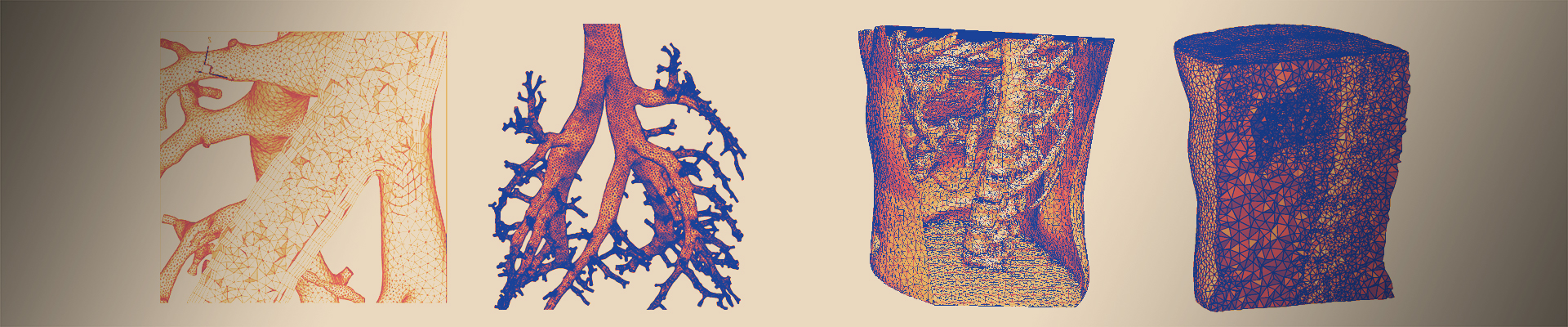
This work is motivated by the needs of the numerical solution of partial differential equations by finite element or finite volume methods. In order to apply these methods, a given domain has to be subdivided into a number of cells with simple geometry. The quality of this subdivision affects the accuracy and convergence of the method. Boundary conforming Delaunay meshes with good quality are the prerequisite for the construction of the Voronoi-box based finite volume method. This method allows to carry over important qualitative properties from the continuous problem to the discretized one. The project is devoted to the construction of boundary conforming Delaunay meshes for three-dimensional domains. [>> more]