Collaborative Research Center 910: Control of self-organizing nonlinear systems: Theoretical methods and concepts of application Subproject A5: Pattern formation in coupled parabolic systems

Project Head:	Prof. Dr. Alexander Mielke
Investigator:	Stefanie Schindler
Funding period III:	January 1, 2019 - Dezember 31, 2022
Previous funding periods:	2011 - 2018, Investigator: Dr. Sina Reichelt

Description

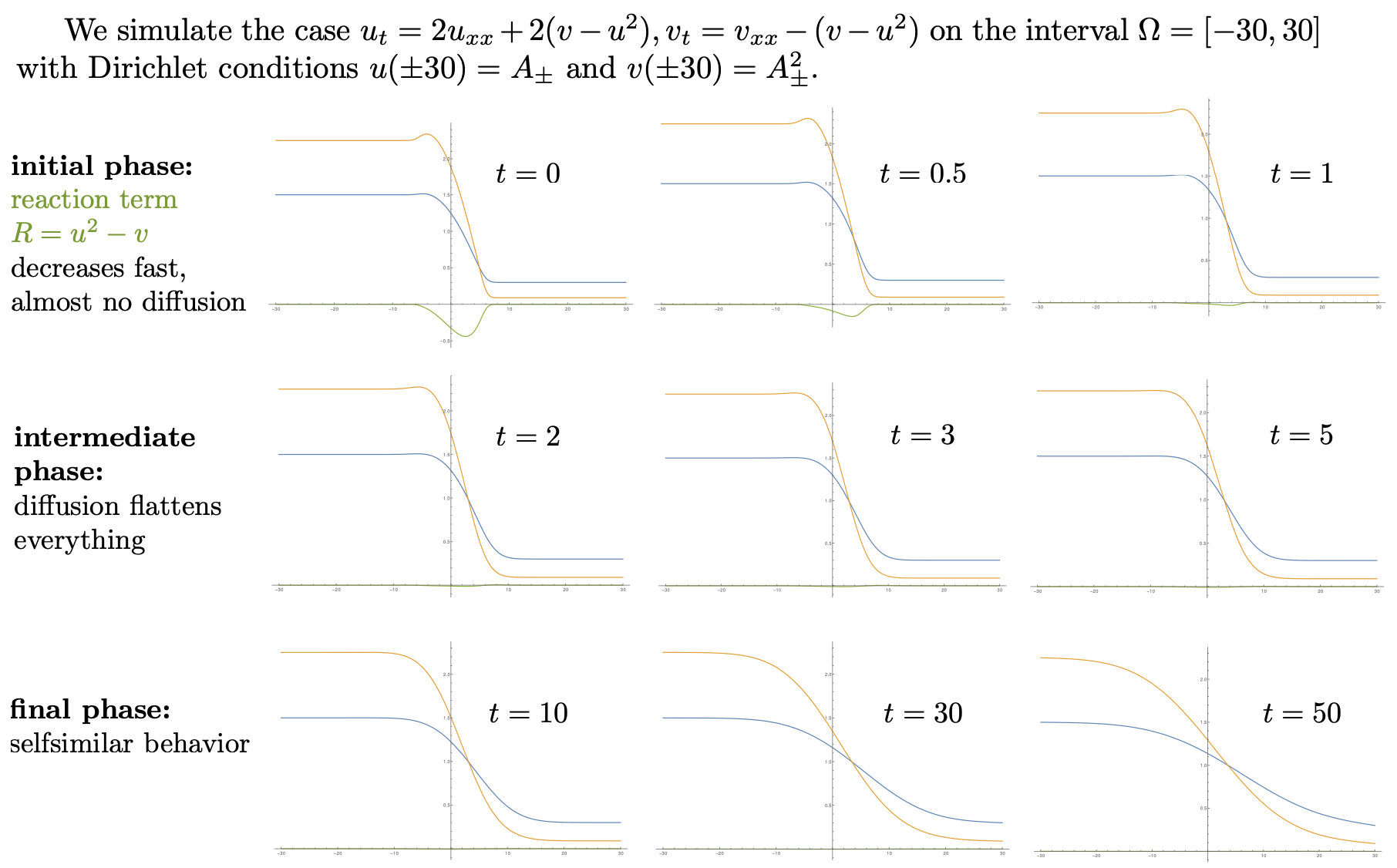
This project studies pattern formation in reaction-diffusion systems and in models of fluid dynamics, such as Kolmogorov's two-equation model for turbulence. In addition to traveling waves, such as fronts and pulses, we also study self-similar structures that describe the asymptotic decay of localized profiles on unbounded domains. On the methodological side we use homogenization techniques for periodically structured materials and evolutionary Gamma-convergence for perturbed gradient flows, which will be combined with self-similar scaling techniques.

---

---

Publications

show hide

• A. Mielke: On two coupled degenerate parabolic equations motivated by thermodynamics, arXiv-Preprint, 2022.
• A. Mielke and S.Reichelt: Traveling fronts in a reaction-diffusion equation with a memory term, J. Dynam. Differ. Eqns. 2022, online first, DOI: 10.1007/s10884-022-10133-6.
• A. Mielke: Relating a rate-independent system and a gradient system for the case of one-homogeneous potentials, J. Dynam. Differ. Eqns. 34, 3143-3164, 2022, DOI: 10.1007/s10884-021-10007-3.
• A. Mielke and J. Naumann: On the existence of global-in-time weak solutions and scaling laws for Kolmogorov's two-equation model of turbulence, Zeitschrift für Angewandte Mathematik und Mechanik 102(9), 1-31, 2022.
• A. Bacho, E. Emmrich, and A. Mielke: An existence result and evolutionary Gamma-convergence for perturbed gradient systems, J. of Evolution Equations 19, 479-522, 2019.
• O. Burylko, A. Mielke, M. Wolfrum, and S. Yanchcopyuk: Coexistence of Hamiltonian-like and dissipative dynamics in chains of coupled phase oscillators with skew-symmetric coupling, SIAM J Appl. Dynam. Syst. 17(3), 2076-2105, 2018.
• M. Becker, Th. Frenzel, Th. Niedermayer, S. Reichelt, A. Mielke, and M. Bär: Local control of globally competing patterns in coupled Swift-Hohenberg equations, Chaos 28(4), 043121, 2018.
• P. Gurevich and S. Reichelt: Pulses in FitzHugh-Nagumo systems with rapidly oscillating coefficients, Multiscale Model. Simul. 16(2), 833-856, 2018.
• S. Reichelt: Corrector estimates for a class of imperfect transmission problems, Asymptot. Anal., 105, 3-26, 2017.
• A. Mielke: Uniform exponential decay for reaction-diffusion systems with complex-balanced mass-action kinetics, in Pattern of Dynamics, Eds. P. Gurevich, J. Hell, B. Sanstede, A. Scheel, Springer Proc. in Math. & Stat. Vol. 205, 149-171, 2017.
• A. Muntean and S. Reichelt: Corrector estimates for a thermo-diffusion model with weak thermal coupling, Multiscale Model. Simul. 16(2), 807-832, 2018.
• S. Reichelt: Error estimates for elliptic equations with not-exactly periodic coefficients, Adv. Math. Sci. Appl., 25, 117-131, 2016.
• S. Reichelt: Two-scale Homogenisation of Systems of Nonlinear Parabolic Equations, PhD Thesis, Humboldt-Universität zu Berlin, 2015.
• A. Mielke: On evolutionary Γ-convergence for gradient systems, in: Lecture Notes in Applied Mathematics and Mechanics, Springer International Publishing, Heidelberg, 187-249, 2016.
• A. Mielke: Deriving effective models for multiscale systems via evolutionary Γ-convergence, in: Control of Self-Organizing Nonlinear Systems, Understanding Complex Systems, Springer, 235-251, 2016.
• W. Dreyer, R. Huth, A. Mielke, J. Rehberg, and M. Winkler: Global existence for a nonlocal and nonlinear Fokker-Planck equation, ZAMP Zeitschrift für Angewandte Mathematik und Physik, 66: 293-315, 2015.
• M. Liero and S. Reichelt: Homogenization of Cahn-Hilliard-type equations via evolutionary Γ-convergence, NoDEA Nonlinear Differential Equations Appl. 25, no. 1, Art. 6, 31 pp., 2018.
• S. Reichelt: Error estimates for nonlinear reaction-diffusion systems involving different length scales, MURPHYS-HSFS-2014: 7th MUlti-Rate Processes and HYSteresis (MURPHYS) & 2nd International Workshop on Hysteresis and Slow-Fast Systems (HSFS), vol. 727 of Journal of Physics: Conference Series, IOP Publishing, 012013/1--012013/15, 2016.
• A. Mielke: Deriving amplitude equations via Γ-convergence, Discr. Cont. Dynam. Systems Ser. A, 35(6), 2679-2700, 2015.
• A. Mielke, S. Reichelt, and M. Thomas: Two-scale homogenization of nonlinear reaction-diffusion systems with small diffusion, Netw. Heterog. Media, 9(2): 353-382, 2014.
copy
• S. Yanchuk, L. Lücken, M. Wolfrum, and A. Mielke: Spectrum and amplitude equations for scalar delay-differential equations with large delay, Discrete Contin. Dyn. Syst., 35(1): 537-553, 2015.
• A. Mielke and E. Rohan: Homogenization of elastic waves in fluid-saturated porous media using the Biot model, Math. Models Meth. Appl. Sci., 23(5): 873-916, 2013.
• A. Mielke, J. Haskovec, and P.A. Markowich: On uniform decay of the entropy for reaction-diffusion systems, J. Dynam. Differential Equations, 27: 897-928, 2015.
• A. Mielke: Multiscale gradient systems and their amplitude equations, Oberwolfach Report 9: 3588-3591, 2012.

---

Posters

show hide

• Stefanie Schindler: Convergence to self-similar profiles for a coupled RDS on the real line, Workshop on "Control of Self-organizing Nonlinear Systems", Wittenberg, September 26-28, 2022.
• Anieza Maltsi, Arbi Moses Badlyan, Willem van Oosterhout, Stefanie Schindler: PDEs in Partial Differential Equations, WIAS Days, March 2-3, 2022.
• M. Heida, A. Mielke, Ch. Kraus, and M. Thomas: Effective models for interfaces with many scales, SCCS Days, Ketzin, October 10-12, 2016.
• M. Becker, Th. Frenzel, Th. Niedermayer, S. Reichelt, A. Mielke, and M. Bär: Competing patterns in anti-symmetrically coupled Swift-hohenberg equations, International Conference on Control of Complex Systems and Networks, Heringsdorf, September 4-8, 2016.
• S. Reichelt: Homogenization of Cahn-Hilliard equations, Conference "Patterns of Dynamics", FU Berlin, July 25-27, 2016.
• S. Reichelt: Homogenization of degenerated reaction-diffusion equations, Doktorandenforum der Leibniz-Gemeinschaft Sektion D, Berlin, June 6-7, 2013.
• M. Thomas: Coupling of reaction diffusion processes with thermomechanics using GENERIC (joint work with A. Mielke), Winter School "Calculus of Variations in Physics and Materials Science", Julius-Maximilians-Universität Würzburg, January 9-13, 2012.

---

Talks

show hide

• S. Schindler: On asymptotic self-similar behavior of solutions to parabolic systems, International Conference on "Control of Self-Organizing Nonlinear Systems", November 25, 2022.
• S. Schindler: Entropy method for a coupled reaction-diffusion system on the real line, Annual workshop of the GAMM Activity Group, October 05, 2022.
• S. Schindler: Entropy method for a coupled reaction-diffusion system on the real line, Langenbach-Seminar, June 29, 2022.
• S. Schindler: Entropy method for a coupled reaction-diffusion system on the real line, Applied Analysis Seminar, University of Graz, online, June 28, 2022.
• S. Schindler: The entropy method for the linear diffusion equation on the whole real line, PhD Seminar WIAS, May 9, 2022.
• A. Mielke: On the existence and longtime behavior of solutions to a degenerate parabolic system, SIAM Conference on Analysis of Partial Differential Equations, online, March, 16, 2022.
• A. Mielke: On two coupled degenerate parabolic equations motivated by thermodynamics, Langenbach-Seminar, online via Zoom, January, 26, 2022.
• A. Mielke: On the longtime behavior of solutions to a coupled degenerate parabolic system motivated by thermodynamics, Nonlinear Waves and Coherent Structures Webinar, online, January, 25, 2022.
• S. Schindler: Energy approach for a coupled reaction-diffusion system on the real line, SFB 910 Symposium "Pattern formation and coherent structures in dissipative systems", online via Zoom, January 14, 2022.
• S. Schindler: Self-similar diffusive equilibration for a coupled reaction-diffusion system with mass-action kinetics, SFB 910 Conference "Control of Self-Organizing Nonlinear Systems", Potsdam, August 29 to September 2, 2021.
• S. Schindler: Self-similar diffusive equilibration for a coupled reaction-diffusion system with mass-action kinetics, Langenbach-Seminar, online via Zoom, June, 30, 2021.
• A. Mielke: Towards a justification of GENERIC: coarse-graining of an infinite-dimensional Hamiltonian systems, Langenbach-Seminar, online via Zoom, Mai, 19, 2021.
• A. Mielke: Convergence for multiscale gradient systems with applications to fast-slow reaction systems, One World Dynamics Seminar, online via Zoom, November, 13, 2020.
• A. Mielke: Similarity solutions for Kolmogorov's two-equation model for turbulence, SFB910 Workshop, TU Berlin, September, 2-3, 2020.
• A. Mielke: On Kolmogorov's two-equation model for turbulence, 90th Annual Meeting of GAMM, Universität/TU Wien, February 18-22, 2019.
• A. Mielke: Traveling fronts in two-scale homogenized reaction-diffusion systems, Analysis Seminar, Universität Bremen, December 18, 2018.
• S. Reichelt: Traveling waves in FitzHugh-Nagumo systems with rapidly oscillating coefficients, SIAM Annual Meeting, Minisymposium "Multiscale analysis and simulation of heterogeneous media", Portland, USA, July, 9-13, 2018.
• S. Reichelt: Pulses in FitzHugh-Nagumo systems with rapidly oscillating coefficients, 89th Annual Meeting of GAMM, Section "Applied Analysis", München, March, 19-23, 2018.
• S. Reichelt: Traveling waves in FitzHugh-Nagumo systems with rapidly oscillating coefficients, SFB 910 Workshop, Wittenberg, August, 29-31, 2017.
• S. Reichelt: Corrector estimates for elliptic and parabolic equations with periodic coefficients,
  Analysis Kolloquium, FAU Erlangen-Nürnberg, May 18, 2017, and Analysis Seminar, Universität Augsburg, May 23, 2017.
• A. Mielke: On self-induced oscillations for friction reduction with applications to walking, Conference "Dynamical Systems and Geometric Mechanics",
  June 12-14, 2017, Technische Universität München, Zentrum für Mathematik, June 13, 2017.
• A. Mielke: Uniform exponential decay for energy-reaction-diffusion systems, Analysis Seminar, University of Pavia, Department of Mathematics, Italien,
  March 21, 2017.
• S. Reichelt: Corrector estimates for a class of imperfect transmission problems, 88th Annual Meeting of GAMM, Weimar, March 6-10, 2017.
June
• A. Mielke: Exponential decay into thermodynamical equilibrium for reaction-diffusion systems with detailed balance, Conference "Patterns of Dynamics", FU Berlin, July 25-27, 2016.
• S. Reichelt: Homogenization of Cahn-Hilliard equations via evolutionary Γ-convergence,
  11th AIMS Conference on Dynamical Systems, Differential Equations, and Applications, Orlando, USA, July 1-5, 2016.
• S. Reichelt: Konvergenz und Homogenisierung, 21. Tag der Mathematik, FU Berlin, April 30, 2016.
• S. Reichelt: Error estimates for elliptic and parabolic equations, Karlstads Universitet, Karlstad, Schweden, April 13, 2016.
• S. Reichelt: Homogenization of Cahn-Hilliard equations via evolutionary Γ-convergence, GAMM-DMV Jahrestagung, Young Researcher's Minisymposium YR1, TU Braunschweig, March 7-11, 2016.
• S. Reichelt: On periodic homogenization, 20th Harz-Seminar, Hahnenklee-Goslar, February 21-23, 2016.
• S. Reichelt: Homogenization of Cahn-Hilliard equations, SFB 910 Workshop, Wittenberg, September 14-19, 2015.
• S. Reichelt: Achilles und die Schildkröte, Lange Nacht der Wissenschaften, Berlin, June 13, 2015.
• A. Mielke: Homogenizing the Penrose-Fife system via evolutionary Γ-convergence, INdAM Workshop ``Special Materials in Complex Systems - SMaCS 2015'', Rome, May 18-20, 2015.
• S. Reichelt: Two-scale homogenization and error estimates for nonlinear reaction-diffusion systems with slow diffusion, CASA Colloquium, TU Eindhoven, March 11, 2015.
• S. Reichelt: Two-scale homogenization and error estimates for nonlinear reaction-diffusion systems, MATHEON Multiscale Seminar, TU Berlin, December 3, 2014.
• degenerate A. Mielke: Homogenization of parabolic gradient systems via evolutionary Γ-convergence, Second Workshop of the GAMM Activity Group on ``Analysis of Partial Differential Equations", Universität Stuttgart, September 29 - October 1, 2014.
• A. Mielke: Multiscale modeling and evolutionary Gamma-convergence for gradient flows, BMS-WIAS Summer School ``Applied Analysis for Materials'', TU Berlin, August 25 - September 5, 2014.
• S. Reichelt: Two-scale homogenization of nonlinear reaction-diffusion systems involving different diffusion length scales, AIMS Conference on Dynamical Systems and Differential Equations, Madrid, June 7-11, 2014
• S. Reichelt: Effective model for a reaction-diffusion system in strongly heterogenous media, MURPHYS-HSFS, WIAS Berlin, April 7-11, 2014.
• A. Mielke: Evolutionary Gamma convergence and amplitude equations, 85th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2014), Friedrich-Alexander Universität Erlangen-Nürnberg, March 10-14, 2014.
• S. Reichelt: Two-scale homogenization of nonlinear reaction-difusion problems with small diffusion, 13th GAMM seminar on microstructures, Bochum, January 17-18, 2014.
• S. Reichelt: Two-scale homogenization of nonlinear reaction-difusion problems with small diffusion, BMS Intensive Course on Evolution Equations and Applications, Berlin, November 27-29, 2013.
• A. Mielke: Introduction to evolutionary Gamma convergence for gradient systems, School "Multi-scale and Multi-field Representations of Condensed Matter Behavior", Centro di Ricerca Matematica "Ennio De Giorgi", Pisa, Italy, November 25-29, 2013.
• M. Thomas: Local versus energetic solutions in rate-independent brittle delamination, Diffuse interface models -- DIMO 2013, Levico (Italy), September 10-13, 2013.
• A. Mielke: Deriving the Ginzburg-Landau equation as amplitude equation via evolutionary Gamma convergence, ERC Workshop on Variational Views on Mechanics and Materials, University of Pavia, June 24-26, 2013.
• June A. Mielke: Gradient structures and uniform global decay for reaction-diffusion systems, Mathematisches Kolloquium, Universität Bielefeld, April 25, 2013.
• S. Reichelt: Introduction toepri homogenization, Seminar, FU Berlin, April 11, 2013.
• A. Mielke: Evolutionary Gamma convergence and amplitude equations, Matheon Multiscale Seminar, TU Berlin, April 8, 2013.
• A. Mielke: Multiscale gradient systems and their amplitude equations, Dynamics of Patterns, Oberwolfach, December 17-21, 2012.
• A. Mielke: Linearized elastoplasticity is the evolutionary Γ-limit of finite elastoplasticity, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), TU Darmstadt, March 26-30, 2012.
• M. Thomas: Delamination in visco-elastic materials with thermal effects, 83th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2012), TU Darmstadt, March 26-30, 2012.
• M. Thomas: Thermomechanical modeling via energy and entropy using GENERIC (joint work with A. Mielke),
  MFO-Workshop "Mechanics of Materials", Oberwolfach, March 18-24, 2012.
• A. Mielke: Gamma convergence and evolution, International Conference "Trends in Mathematical Analysis", Politecnico di Milano, March 1-3, 2012.
• M. Thomas: Thermomechanical modeling via energy and entropy (joint work with A. Mielke), University of Pavia, February 14, 2012.
• S. Reichelt: Homogenization in reaction-diffusion problems, SFB 910 Symposium, TU Berlin, November 25, 2011.
• S. Reichelt: Homogenization in reaction-diffusion problems, SFB 910 Workshop, Wittenberg, August 31 - September 2, 2011.

---

Symposia and Workshops

show hide

• March 14-18, 2022: Nonlinear Parabolic Equations and Systems, SIAM Conference on Analysis of Partial Differential Equations, online, organized by William E. Fitzgibbon (Univ. Houston), A. Mielke (SFB 910), Hong-Ming Yin (Washington State Univ.).
• January 14, 2022: Pattern formation and coherent structures in dissipative systems, SFB 910 Symposium, online via Zoom.
• October 30, 2020: Colloquium of SFB 910 in cooperation with the Thematic Einstein Semester 2020/21 "Energy-based mathematical methods for reactive multiphase flows" organized by TU Berlin (V. Mehrmann) and WIAS (M. Liero, A. Mielke, D. Peschka, M. Thomas, B. Wagner).
• September 24-28, 2018: Analysis of Evolutionary and Complex Systems, WIAS Berlin.
• October 4-6, 2017: Homogenization Theory and Applications, WIAS Berlin.
• May 18, 2012: Mathematical methods in multiscale systems, SFB 910 Symposium, TU Berlin.
• Further events at SFB 910