The phenomenon of coagulation occurs in a wide range of applications, e.g., in physics (aggregation of particles, growth of gas bubbles), meteorology (merging of drops in atmospheric clouds, aerosol transport), chemistry (hydrogels, reacting polymers, soot formation) and astrophysics (formation of stars and planets).
Key questions include the number or concentration of particles with different sizes or ranges of sizes and shapes as well as their distribution in space. A common tool for the mathematical treatment of the subject are nonlinear partial integro-differential equations. In particular, the time evolution of the average concentration of objects of a given size are often described by Smoluchowski's coagulation equation and its spatially inhomogeneous extensions. However, the Smoluchowski description sometimes breaks down and then stochastic interacting particle systems are important for identifying how to augment or replace the Smoluchowski equation. The particle systems are also an important source of numerical approximations.
A form of explosive coagulation known as gelation arises in some situations and leads to a phase transition: At a critical time one finds for the first time that a positive fraction of the total mass of particles in the system is collected into a single aggregate. This might be observed as fine dust forming well defined clumps, but it is better known when a previously liquid mixture turns into a a gel (something like a jelly), because dissolved or suspended material has undergone so many local coagulations that a wide reaching network arises, immobilising the remaining fluid.
Contribution of the Institute
Aspects of the gelation phase transition mentioned above are currently the main focus of the work at WIAS on coagulation. This has highlighted connections to random graph (network) models, which arise when one regards coagulating particles as the nodes of a graph and indicates coagulation of two particles by adding an edge connecting them in the graph (a connection in the network).
Questions of gelation are particularly interesting in spatially resolved systems of coagulating particles where coagulation is, to a significant extent, controlled by the rate at which particles meet (e.g. diffusion limited aggregation). To resolve questions in this field we are developing new mathematical methods using tools from the areas of large deviations and random graphs.
Many coagulation processes in chemical engineering have been successfully modelled by stochastic particle systems in recent years. For example, the formation of soot particles in combustion systems is a highly complex process, which needs rather sophisticated modelling of the resulting soot particle populations. The stochastic approach allows for very detailed models of individual particles to be included with little additional impact on computation times.
In collaboration with the Department of Chemical Engineering and Biotechnology (University of Cambridge, UK), a mathematical model for such processes has been developed. In this model, each particle is described by its constituent primary particles and the connectivity between these primaries (see Figure). Each primary in turn has internal variables that describe its chemical composition.
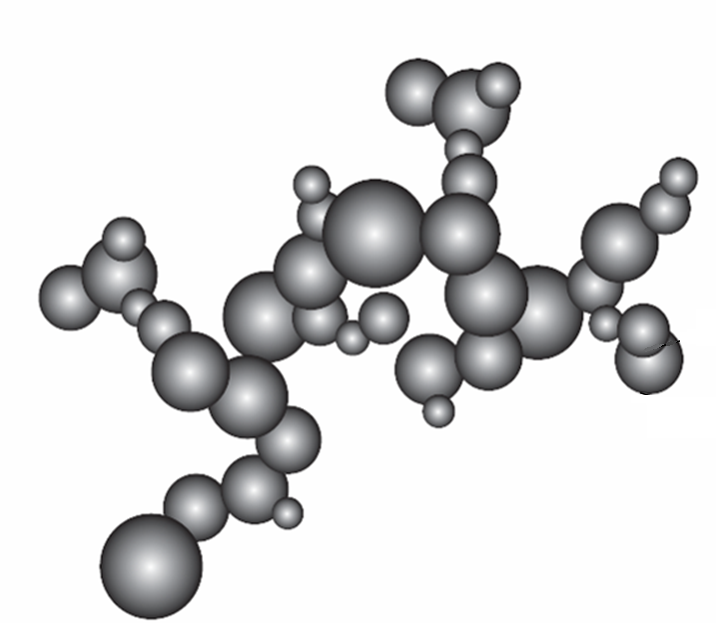
Stochastic weighted algorithms were applied to this multidimensional particle model. The weighting mechanisms are designed in such a way that various physical processes changing individual particles (such as growth, or other surface reactions) can be treated by the algorithms. A spatially resolved stochastic particle model for coagulation-advection problems in bounded domains with inception at the boundary was studied. Convergence of the particle system to a deterministic limit was proved. It was demonstrated that stochastic weighted algorithms can be successfully used with realistic coagulation kernels and high dimensional particle models.
Stochastic particle methods depend on several discretization parameters, due to the finite number of particles, the decoupling of transport and interaction (time step), and the spatial delocalization of the interaction (cell size). The dependence on the cell size of the steady state solution obtained in the infinite-particle-number limit was studied. This work was then combined with fluid dynamics simulations to study the formation of particles in turbulent flows, see the topic Numerical methods for the simulation of population balance systems.
Publications
 Articles in Refereed Journals
Articles in Refereed Journals
-
D. Heydecker, R.I.A. Patterson, A bilinear flory equation, Annales de l'Institut Henri Poincare. Probabilites et Statistiques, 60 (2024), pp. 2508--2548, DOI 10.1214/23-aihp1409 .
Abstract
We consider coagulation equations of Smoluchowski or Flory type where the total merge rate has a bilinear form π(y) · Aπ (x) for a vector of conserved quantities π, generalising the multiplicative kernel. For these kernels, a gelation transition occurs at a finite time tg ∈ (0,∞), which can be given exactly in terms of an eigenvalue problem in finite dimensions. We prove a hydrodynamic limit for a stochastic coagulant, including a corresponding phase transition for the largest particle, and exploit a coupling to random graphs to extend analysis of the limiting process beyond the gelation time. -
L. Andreis, W. König, H. Langhammer, R.I.A. Patterson, A large-deviations principle for all the components in a sparse inhomogeneous random graph, Probability Theory and Related Fields, 186 (2023), pp. 521--620, DOI 10.1007/s00440-022-01180-7 .
Abstract
We study an inhomogeneous sparse random graph, GN, on [N] = { 1,...,N } as introduced in a seminal paper [BJR07] by Bollobás, Janson and Riordan (2007): vertices have a type (here in a compact metric space S), and edges between different vertices occur randomly and independently over all vertex pairs, with a probability depending on the two vertex types. In the limit N → ∞ , we consider the sparse regime, where the average degree is O(1). We prove a large-deviations principle with explicit rate function for the statistics of the collection of all the connected components, registered according to their vertex type sets, and distinguished according to being microscopic (of finite size) or macroscopic (of size ≈ N). In doing so, we derive explicit logarithmic asymptotics for the probability that GN is connected. We present a full analysis of the rate function including its minimizers. From this analysis we deduce a number of limit laws, conditional and unconditional, which provide comprehensive information about all the microscopic and macroscopic components of GN. In particular, we recover the criterion for the existence of the phase transition given in [BJR07]. -
P. Ral, A.K. Giri, V. John, Instantaneous gelation and non-existence of weak solutions for the Oort--Hulst--Safronov coagulation model, Proceedings of The Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences, 479 (2023), pp. 20220385/1--20220385/13, DOI 10.1098/rspa.2022.0385 .
Abstract
The possible occurrence of instantaneous gelation to the Oort--Hulst--Safronov (OHS) coagulation equation is investigated for a certain class of unbounded coagulation kernels. The existence of instantaneous gelation is confirmed by showing the non-existence of mass-conserving weak solutions. Finally, it is shown that for such kernels, there is no weak solution to the OHS coagulation equation at any time interval. -
L. Andreis, W. König, R.I.A. Patterson, A large-deviations principle for all the cluster sizes of a sparse Erdős--Rényi random graph, Random Structures and Algorithms, 59 (2021), pp. 522--553, DOI 10.1002/rsa.21007 .
Abstract
A large-deviations principle (LDP) is derived for the state, at fixed time, of the multiplicative coalescent in the large particle number limit. The rate function is explicit and describes each of the three parts of the state: microscopic, mesoscopic and macroscopic. In particular, it clearly captures the well known gelation phase transition given by the formation of a particle containing a positive fraction of the system mass at time t=1. Via a standard map of the multiplicative coalescent onto a time-dependent version of the Erdős-Rényi random graph, our results can also be rephrased as an LDP for the component sizes in that graph. Our proofs rely on estimates and asymptotics for the probability that smaller Erdős-Rényi graphs are connected. -
C. Bartsch, V. Wiedmeyer, Z. Lakdawala, R.I.A. Patterson, A. Voigt, K. Sundmacher, V. John, Stochastic-deterministic population balance modeling and simulation of a fluidized bed crystallizer experiment, Chemical Engineering Sciences, 208 (2019), pp. 115102/1--115102/14, DOI 10.1016/j.ces.2019.07.020 .
-
A.D. Mcguire, S. Mosbach, G. Reynolds, R.I.A. Patterson, E.J. Bringley, N.A. Eaves, J. Dreyer, M. Kraft, Analysing the effect of screw configuration using a stochastic twin-screw granulation model, Chemical Engineering Sciences, 203 (2019), pp. 358--379, DOI https://doi.org/10.1016/j.ces.2019.03.078 .
-
C. Bartsch, V. John, R.I.A. Patterson, Simulations of an ASA flow crystallizer with a coupled stochastic-deterministic approach, Comput. Chem. Engng., 124 (2019), pp. 350--363, DOI 10.1016/j.compchemeng.2019.01.012 .
Abstract
A coupled solver for population balance systems is presented, where the flow, temperature, and concentration equations are solved with finite element methods, and the particle size distribution is simulated with a stochastic simulation algorithm, a so-called kinetic Monte-Carlo method. This novel approach is applied for the simulation of an axisymmetric model of a tubular flow crystallizer. The numerical results are compared with experimental data. -
A. Mielke, R.I.A. Patterson, M.A. Peletier, D.R.M. Renger, Non-equilibrium thermodynamical principles for chemical reactions with mass-action kinetics, SIAM Journal on Applied Mathematics, 77 (2017), pp. 1562--1585, DOI 10.1137/16M1102240 .
Abstract
We study stochastic interacting particle systems that model chemical reaction networks on the micro scale, converging to the macroscopic Reaction Rate Equation. One abstraction level higher, we study the ensemble of such particle systems, converging to the corresponding Liouville transport equation. For both systems, we calculate the corresponding large deviations and show that under the condition of detailed balance, the large deviations induce a non-linear relation between thermodynamic fluxes and free energy driving force. -
R.I.A. Patterson, S. Simonella, W. Wagner, A kinetic equation for the distribution of interaction clusters in rarefied gases, Journal of Statistical Physics, 169 (2017), pp. 126--167.
-
R.I.A. Patterson, Properties of the solutions of delocalised coagulation and inception problems with outflow boundaries, Journal of Evolution Equations, 16 (2016), pp. 261--291.
Abstract
Well posedness is established for a family of equations modelling particle populations undergoing delocalised coagulation, advection, inflow and outflow in a externally specified velocity field. Very general particle types are allowed while the spatial domain is a bounded region of $d$-dimensional space for which every point lies on exactly one streamline associated with the velocity field. The problem is formulated as a semi-linear ODE in the Banach space of bounded measures on particle position and type space. A local Lipschitz property is established in total variation norm for the propagators (generalised semi-groups) associated with the problem and used to construct a Picard iteration that establishes local existence and global uniqueness for any initial condition. The unique weak solution is shown further to be a differentiable or at least bounded variation strong solution under smoothness assumptions on the parameters of the coagulation interaction. In the case of one spatial dimension strong differentiability is established even for coagulation parameters with a particular bounded variation structure in space. This one dimensional extension establishes the convergence of the simulation processes studied in [Patterson, Stoch. Anal. Appl. 31, 2013] to a unique and differentiable limit. -
R.I.A. Patterson, W. Wagner, Cell size error in stochastic particle methods for coagulation equations with advection, SIAM Journal on Numerical Analysis, 52 (2014), pp. 424--442.
Abstract
The paper studies the approximation error in stochastic particle methods for spatially inhomogeneous population balance equations. The model includes advection, coagulation and inception. Sufficient conditions for second order approximation with respect to the spatial discretization parameter (cell size) are provided. Examples are given, where only first order approximation is observed. -
M. Sander, R.I.A. Patterson, A. Braumann, A. Raj, M. Kraft, Developing the PAH-PP soot particle model using process informatics and uncertainty propagation, Proceedings of the Combustion Institute, 33 (2011), pp. 675--683.
Abstract
n this work we present the new PAH-PP soot model and use a data collaboration approach to determine some of its parameters. The model describes the formation, growth and oxidation of soot in laminar premixed flames. Soot particles are modelled as aggregates containing primary particles, which are built from polycyclic aromatic hydrocarbons (PAHs), the main building blocks of a primary particle (PP). The connectivity of the primary particles is stored and used to determine the rounding of the soot particles due to surface growth and condensation processes. Two neighbouring primary particles are replaced by one if the coalescence level between the two primary particles reaches a threshold. The model contains, like most of the other models, free parameters that are unknown a priori. The experimental premixed flame data from Zhao et al. [B. Zhao, Z. Yang, Z. Li, M.V. Johnston, H. Wang, Proc. Combust. Inst. 30 (2) (2005) 1441?1448] have been used to estimate the smoothing factor of soot particles, the growth factor of PAHs within particles and the soot density using a low discrepancy series method with a subsequent response surface optimisation. The optimised particle size distributions show good agreement with the experimental ones. The importance of a standardised data mining system in order to optimise models is underlined. -
R.I.A. Patterson, W. Wagner, M. Kraft, Stochastic weighted particle methods for population balance equations, Journal of Computational Physics, 230 (2011), pp. 7456--7472.
Abstract
A class of stochastic algorithms for the numerical treatment of population balance equations is introduced. The algorithms are based on systems of weighted particles, in which coagulation events are modelled by a weight transfer that keeps the number of computational particles constant. The weighting mechanisms are designed in such a way that physical processes changing individual particles (such as growth, or other surface reactions) can be conveniently treated by the algorithms. Numerical experiments are performed for complex laminar premixed flame systems. Two members of the class of stochastic weighted particle methods are compared to each other and to a direct simulation algorithm. One weighted algorithm is shown to be consistently better than the other with respect to the statistical noise generated. Finally, run times to achieve fixed error tolerances for a real flame system are measured and the better weighted algorithm is found to be up to three times faster than the direct simulation algorithm. -
M. Celnik, R.I.A. Patterson, M. Kraft, W. Wagner, A predictor-corrector algorithm for the coupling of stiff ODEs to a particle population balance, Journal of Computational Physics, 228 (2009), pp. 2758--2769.
-
M. Celnik, R.I.A. Patterson, M. Kraft, W. Wagner, Coupling a stochastic soot population balance to gas-phase chemistry using operator splitting, , 148 (2007), pp. 158-176.
-
N. Morgan, C. Wells, M. Goodson, M. Kraft, W. Wagner, A new numerical approach for the simulation of the growth of inorganic nanoparticles, Journal of Computational Physics, 211 (2006), pp. 638--658.
-
R.I.A. Patterson, J. Singh, M. Balthasar, M. Kraft, W. Wagner, Extending stochastic soot simulation to higher pressures, Combustion and Flame, 145 (2006), pp. 638-642.
-
C. Wells, N. Morgan, M. Kraft, W. Wagner, A new method for calculating the diameters of partially-sintered nanoparticles and its effect on simulated particle properties, , 61 (2006), pp. 158--166.
-
M. Kraft, S. Mosbach, W. Wagner, Using a web module to teach stochastic modelling, Chemical Engineering Education, 39 (2005), pp. 244-248.
-
N. Morgan, W. Wells, M. Kraft, W. Wagner, Modelling nanoparticle dynamics: Coagulation, sintering, particle inception and surface growth, Combustion Theory and Modelling, 9 (2005), pp. 449--461.
-
J. Singh, M. Balthasar, M. Kraft, W. Wagner, Stochastic modeling of soot particle size and age distributions in laminar premixed flames, Proceedings of the Combustion Institute, 30 (2005), pp. 1457-1465.
-
C. Lecot, W. Wagner, A quasi-Monte Carlo scheme for Smoluchowski's coagulation equation, Mathematics of Computation, 73 (2004), pp. 1953-1966.
-
M. Kraft, W. Wagner, An improved stochastic algorithm for temperature-dependent homogeneous gas phase reactions, Journal of Computational Physics, 185 (2003), pp. 139--157.
-
M. Kraft, W. Wagner, Numerical study of a stochastic particle method for homogeneous gas phase reactions, Computers & Mathematics with Applications. An International Journal, 45 (2003), pp. 329--349.
-
W. Wagner, Stochastic, analytic and numerical aspects of coagulation processes, Mathematics and Computers in Simulation, 62 (2003), pp. 265--275.
 Contributions to Collected Editions
Contributions to Collected Editions
-
D. Knees, R. Kornhuber, Ch. Kraus, A. Mielke, J. Sprekels, C3 -- Phase transformation and separation in solids, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 189--203.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
L. Andreis, T. Iyer, E. Magnanini, Convergence of cluster coagulation dynamics, Preprint no. 3182, WIAS, Berlin, 2025, DOI 10.20347/WIAS.PREPRINT.3182 .
Abstract, PDF (435 kByte)
We study hydrodynamic limits of the cluster coagulation model; a coagulation model introduced by Norris [Comm. Math. Phys., 209(2):407-435 (2000)]. In this process, pairs of particles x,y in a measure space E, merge to form a single new particle z according to a transition kernel K(x, y, dz), in such a manner that a quantity, one may regard as the total emphmass of the system, is conserved. This model is general enough to incorporate various inhomogeneities in the evolution of clusters, for example, their shape, or their location in space. We derive sufficient criteria for trajectories associated with this process to concentrate among solutions of a generalisation of the emphFlory equation, and, in some special cases, by means of a uniqueness result for solutions of this equation, prove a weak law of large numbers. This multi-type Flory equation is associated with emphconserved quantities associated with the process, which may encode different information to conservation of mass (for example, conservation of centre of mass in spatial models). We also apply criteria for emphgelation in this process to derive sufficient criteria for this equation to exhibit emphgelling solutions. When this occurs, this multi-type Flory equation encodes, via the associated conserved property, the interaction between the emphgel and the finite size emphsol particles. -
L. Andreis, W. König, H. Langhammer, R.I.A. Patterson, Spatial particle processes with coagulation: Gibbs-measure approach, gelation and Smoluchowski equation, Preprint no. 3086, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3086 .
Abstract, PDF (651 kByte)
We study a spatial Markovian particle system with pairwise coagulation, a spatial version of the Marcus--Lushnikov process: according to a coagulation kernel K, particle pairs merge into a single particle, and their masses are united. We introduce a statistical-mechanics approach to the study of this process. We derive an explicit formula for the empirical process of the particle configuration at a given fixed time T in terms of a reference Poisson point process, whose points are trajectories that coagulate into one particle by time T. The non-coagulation between any two of them induces an exponential pair-interaction, which turns the description into a many-body system with a Gibbsian pair-interaction. Based on this, we first give a large-deviation principle for the joint distribution of the particle histories (conditioning on an upper bound for particle sizes), in the limit as the number N of initial atoms diverges and the kernel scales as 1/N K. We characterise the minimiser(s) of the rate function, we give criteria for its uniqueness and prove a law of large numbers (unconditioned). Furthermore, we use the unique minimiser to construct a solution of the Smoluchowski equation and give a criterion for the occurrence of a gelation phase transition. endabstract -
L. Andreis, T. Iyer, E. Magnanini, Gelation, hydrodynamic limits and uniqueness in cluster coagulation processes, Preprint no. 3039, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3039 .
Abstract, PDF (495 kByte)
We consider the problem of gelation in the cluster coagulation model introduced by Norris [Comm. Math. Phys., 209(2):407-435 (2000)]; this model is general enough to incorporate various inhomogenieties in the evolution of clusters, for example, their shape, or their location in space. We derive general, sufficient criteria for stochastic gelation in this model, and for trajectories associated with this process to concentrate among solutions of a generalisation of the Flory equation; thus providing sufficient criteria for the equation to have gelling solutions. As particular cases, we extend results related to the classical Marcus-Lushnikov coagulation process and Smoluchowski coagulation equation, showing that reasonable 'homogenous' coagulation processes with exponent γ larger than 1 yield gelation. In another special case, we prove a law of large numbers for the trajectory of the empirical measure of the stochastic cluster coagulation process, by means of a uniqueness result for the solution of the aforementioned generalised Flory equation. Finally, we use coupling arguments with inhomogeneous random graphs to deduce sufficient criterion for strong gelation (the emergence of a particle of size O(N)). -
D. Heydecker, R.I.A. Patterson, Bilinear coagulation equations, Preprint no. 2637, WIAS, Berlin, 2019, DOI 10.20347/WIAS.PREPRINT.2637 .
Abstract, PDF (453 kByte)
We consider coagulation equations of Smoluchowski or Flory type where the total merge rate has a bilinear form π(y) · Aπ (x) for a vector of conserved quantities π, generalising the multiplicative kernel. For these kernels, a gelation transition occurs at a finite time tg ∈ (0,∞), which can be given exactly in terms of an eigenvalue problem in finite dimensions. We prove a hydrodynamic limit for a stochastic coagulant, including a corresponding phase transition for the largest particle, and exploit a coupling to random graphs to extend analysis of the limiting process beyond the gelation time. -
R.I.A. Patterson, D.R.M. Renger, Dynamical large deviations of countable reaction networks under a weak reversibility condition, Preprint no. 2273, WIAS, Berlin, 2016, DOI 10.20347/WIAS.PREPRINT.2273 .
Abstract, PDF (343 kByte)
A dynamic large deviations principle for a countable reaction network including coagulation--fragmentation models is proved. The rate function is represented as the infimal cost of the reaction fluxes and a minimiser for this variational problem is shown to exist. A weak reversibility condition is used to control the boundary behaviour and to guarantee a representation for the optimal fluxes via a Lagrange multiplier that can be used to construct the changes of measure used in standard tilting arguments. Reflecting the pure jump nature of the approximating processes, their paths are treated as elements of a BV function space.
 Talks, Poster
Talks, Poster
-
J. Köppl, Condensation with Optimal Rate and Excitation Spectrum for Bose Gases in the Gross-Pitaevskii Limit, Arbeitsgemeinschaft: Analysis of Many-body Quantum Systems, October 5 - 10, 2025, Mathematisches Forschungsinstitut Oberwolfach.
-
E. Magnanini, A Markovian particle system with coagulation, Oberseminar Stochastik, Universität zu Kö ln, Department Mathematik/Informatik, January 22, 2025.
-
E. Magnanini, Gelation and hydrodynamic limits in cluster coagulation processes, 4th Italian Meeting on Probability and Mathematical Statistics, June 10 - 14, 2024, University of Rome, Tor Vergata, Sapienza University of Rome, The University of Roma Tre, LUISS, Rome, Italy, June 14, 2024.
-
E. Magnanini, Spatial coagulation and gelation, Random Geometric Systems, Third Annual Conference of SPP 2265, October 28 - 30, 2024, Harnack-Haus, Tagungsstätte der Max-Planck-Gesellschaft, October 29, 2024.
-
H. Langhammer, A large-deviations principle for all the components in a sparse inhomogeneous random graph, Workshop ``Random Graphs: Combinatorics, Complex Networks and Disordered Systems", March 27 - 31, 2023, Mathematisches Forschungsinstitut Oberwolfach, Oberwolfach, March 28, 2023.
-
E. Magnanini, Gelation and hydrodynamic limits in a spatial Marcus--Lushnikov process, In Search of Model Structures for Non-equilibrium Systems, Münster, April 24 - 28, 2023.
-
E. Magnanini, Gelation and hydrodynamic limits in a spatial Marcus--Lushnikov process, Workshop ``In search of model structures for non-equilibrium systems'', April 24 - 28, 2023, Westfälische Wilhelms-Universität Münster, Fachbereich Mathematik und Informatik, April 25, 2023.
-
E. Magnanini, Gelation in a spatial Marcus--Lushnikov process, Workshop MathMicS 2023: Mathematics and Microscopic Theory for Random Soft Matter Systems, Düsseldorf, February 13 - 15, 2023.
-
E. Magnanini, Gelation in a spatial Marcus--Lushnikov process, Workshop MathMicS 2023: Mathematics and microscopic theory for random Soft Matter systems, February 13 - 15, 2023, Heinrich-Heine-Universität Düsseldorf, Institut für Theoretische Physik II - Soft Matter, February 14, 2023.
-
E. Magnanini, Spatial coagulation and gelation, SPP2265-Reviewer-Kolloquium, Köln, August 29, 2023.
-
B. Jahnel, Percolation, Oberseminar, Technische Universität Braunschweig, Institut für Mathematische Stochastik, November 8, 2023.
-
D.R.M. Renger, Macroscopic fluctuation theory of chemical reaction networks, Workshop on Chemical Reaction Networks, July 1 - 3, 2019, Politecnico di Torino, Dipartimento di Scienze Matematiche ``G. L. Lagrange``, Italy, July 2, 2019.
-
L. Andreis, A large-deviations approach to the multiplicative coagulation process, Workshop ``Woman in Probability'', May 31 - June 1, 2019, Technische Universität München, Fakultät für Mathematik, May 31, 2019.
-
L. Andreis, Coagulating particles and gelation phase transition: A large-deviation approach, Second Italian Meeting on Probability and Mathematical Statistics, June 17 - 20, 2019, Vietri sul Mare, Italy, June 19, 2019.
-
L. Andreis, Large-deviation approach to coagulation processes and gelation, Workshop on Chemical Reaction Networks, July 1 - 3, 2019, Politecnico di Torino, Dipartimento di Scienze Matematiche ''G. L. Lagrange``, Italy, July 2, 2019.
-
L. Andreis, Phase transitions in coagulation processes and random graphs, Workshop ``Welcome Home 2019'', December 19 - 20, 2019, Università di Torino, Dipartimento di Matematica ``G. Peano'', Italy, December 19, 2019.
-
R.I.A. Patterson, A novel simulation method for stochastic particle systems, Seminar, Department of Chemical Engineering and Biotechnology, University of Cambridge, Faculty of Mathematics, UK, May 9, 2019.
-
R.I.A. Patterson, Interaction clusters for the Kac process, Berlin--Leipzig Workshop in Analysis and Stochastics, January 16 - 18, 2019, Max-Planck-Institut für Mathematik in den Naturwissenschaften, Leipzig, January 18, 2019.
-
R.I.A. Patterson, Interaction clusters for the Kac process, Workshop on Effective Equations: Frontiers in Classical and Quantum Systems, June 24 - 28, 2019, Hausdorff Research Institute for Mathematics, Bonn, June 28, 2019.
-
R.I.A. Patterson, Kinetic interaction clusters, Oberseminar, Martin-Luther-Universität Halle-Wittenberg, Naturwissenschaftliche Fakultät II -- Chemie, Physik und Mathematik, April 17, 2019.
-
L. Andreis, A large-deviations approach to the multiplicative coagulation process, Probability Seminar, Università degli Studi di Padova, Dipartimento di Matematica ``Tullio Levi--Civita'', Italy, October 12, 2018.
-
L. Andreis, A large-deviations approach to the multiplicative coagulation process, Seminar ''Theory of Complex Systems and Neurophysics --- Theory of Statistical Physics and Nonlinear Dynamics``, Humboldt-Universität zu Berlin, Institut für Physik, October 30, 2018.
-
D.R.M. Renger, Gradient flows and GENERIC in flux space, Workshop ``Variational Methods for Evolution'', November 12 - 18, 2017, Mathematisches Forschungsinstitut Oberwolfach, November 16, 2017.
-
R.I.A. Patterson, Confidence intervals for coagulation--advection simulations, Clausthal-Göttingen International Workshop on Simulation Science, April 27 - 28, 2017, Georg-August-Universität Göttingen, Institut für Informatik, April 28, 2017.
-
R.I.A. Patterson, Coagulation --- Transport Simulations with Stochastic Particles, CIM-WIAS Workshop ``Topics in Applied Analysis and Optimisation'', December 6 - 8, 2017, University of Lisbon, International Center for Mathematics, Lisboa, Portugal, December 7, 2017.
-
R.I.A. Patterson, Simulation of particle coagulation and advection, Numerical Methods and Applications of Population Balance Equations, October 13, 2017, GRK 1932, Technische Universität Kaiserslautern, Fachbereich Mathematik, October 13, 2017.
-
R.I.A. Patterson, Monte Carlo simulation of soot, King Abdullah University of Science and Technology (KAUST), Clean Combustion Research Center, Thuwal, Saudi Arabia, January 11, 2016.
-
R.I.A. Patterson, Population balance simulation, University of Cambridge, Department for Chemical Engineering and Biotechnology, UK, May 5, 2016.
-
R.I.A. Patterson, Simulations of flame generated particles, Advances in Uncertainty Quantification Methods, Algorithms and Applications (UQAW 2016), January 5 - 10, 2016, King Abdullah University of Science and Technology (KAUST), Thuwal, Saudi Arabia, January 5, 2016.
-
D.R.M. Renger, Large deviations for reacting particle systems: The empirical and ensemble processes, Workshop ``Interplay of Analysis and Probability in Applied Mathematics'', July 26 - August 1, 2015, Mathematisches Forschungsinstitut Oberwolfach, Oberwolfach, July 30, 2015.
-
D.R.M. Renger, The empirical process of reacting particles: Large deviations and thermodynamic principles, Minisymposium ``Real World Phenomena Explained by Microscopic Particle Models'' of the 8th International Congress on Industrial and Applied Mathematics (ICIAM 2015), August 8 - 22, 2015, International Council for Industrial and Applied Mathematics, Beijing, China, August 10, 2015.
-
R.I.A. Patterson, Approximation errors for Smoluchowski simulations, 10 th IMACS Seminar on Monte Carlo Methods, July 6 - 10, 2015, Johannes Kepler Universität Linz, Austria, July 7, 2015.
-
R.I.A. Patterson, Particle systems, kinetic equations and their simulation, 8th International Congress on Industrial and Applied Mathematics, ICIAM 2015, August 8 - 15, 2015, CNCC - China National Convention Center, Beijing, China.
-
R.I.A. Patterson, Uniqueness and regularity for coagulation-advection problems, Workshop on Theory and Numerics of Kinetic Equations, June 1 - 4, 2015, Universität Saarbrücken, June 2, 2015.
-
R.I.A. Patterson, Convergence of coagulation-advection simulations, Workshop on Particle Transport with Emphasis on Stochastics, November 6 - 7, 2014, Aarhus University, Denmark, November 6, 2014.
-
R.I.A. Patterson, Monte Carlo simulation of nano-particle formation, University of Technology Eindhoven, Institute for Complex Molecular Systems, Netherlands, September 5, 2013.
-
R.I.A. Patterson, Stochastic methods for particle coagulation problems in flows with boundaries, 5th Workshop ``Theory and Numerics of Kinetic Equations'', May 13 - 15, 2013, Universität des Saarlandes, Saarbrücken, May 14, 2013.
-
W. Wagner, Stochastic particle methods for population balance equations, 5th Workshop ``Theory and Numerics of Kinetic Equations'', May 13 - 15, 2013, Universität des Saarlandes, Saarbrücken, May 13, 2013.
-
W. Wagner, Stochastic particle methods for coagulation problems, 28th International Symposium on Rarefied Gas Dynamics, July 9 - 13, 2012, University of Zaragoza, Spain, July 9, 2012.
-
W. Wagner, Fragmentation equations and stochastic models, Workshop ``Asymptotic Methods for Dissipative Particle Systems'', May 18 - 22, 2009, University of California, Institute for Pure and Applied Mathematics, Los Angeles, USA, May 18, 2009.
-
W. Wagner, Fragmentation models, Workshop on Theory and Applications of Classical and Quantum Kinetic Theory, June 21 - 26, 2009, Banff International Research Station for Mathematical Innovation and Discovery, Canada, June 23, 2009.
-
W. Wagner, Introduction to Markov jump processes, Scuola Superiore di Catania, Laboratory for Complex Systems, Italy, October 27, 2009.
-
W. Wagner, Random and deterministic fragmentation models, Seventh IMACS Seminar on Monte Carlo Methods (MCM2009), September 6 - 11, 2009, Université Libre de Bruxelles, Brussels, Belgium, September 7, 2009.
-
W. Wagner, Explosion properties of random fragmentation models, Workshop ``Coagulation et Fragmentation Stochastiques'', April 15 - 18, 2008, Université Paris VI, Laboratoire de Probabilités, France, April 16, 2008.
-
W. Wagner, Explosion properties of random fragmentation models, Università di Catania, Dipartimento di Matematica e Informatica, Italy, May 8, 2008.
-
W. Wagner, Stochastic models for coagulation-fragmentation processes, Workshop on Coagulation-Fragmentation Processes: Theory and Application, July 4 - 8, 2005, University of Edinburgh, UK, July 5, 2005.
-
W. Wagner, Modelling nanoparticle dynamics: Coagulation, sintering, particle inception and surface growth, MC$^2$QMC 2004, June 7 - 10, 2004, Juan-les-Pins, France, June 7, 2004.
-
W. Wagner, Numerical simulation of coagulation dynamics using quasi-random numbers, MC$^2$QMC 2004, June 7 - 10, 2004, Juan-les-Pins, France, June 7, 2004.
-
W. Wagner, A quasi-Monte Carlo simulation of cluster coagulation, IV IMACS Seminar on Monte Carlo Methods, September 15 - 19, 2003, Berlin, September 18, 2003.
 External Preprints
External Preprints
-
L. Andreis, T. Iyer, E. Magnanini, Convergence of cluster coagulation dynamics, Preprint no. arXiv:2406.12401, Cornell University, 2024, DOI 10.48550/arXiv.2406.12401 .
Abstract
We study hydrodynamic limits of the cluster coagulation model; a coagulation model introduced by Norris [Comm. Math. Phys., 209(2):407-435 (2000)]. In this process, pairs of particles x,y in a measure space E, merge to form a single new particle z according to a transition kernel K(x,y,dz), in such a manner that a quantity, one may regard as the total mass of the system, is conserved. This model is general enough to incorporate various inhomogeneities in the evolution of clusters, for example, their shape, or their location in space. We derive sufficient criteria for trajectories associated with this process to concentrate among solutions of a generalisation of the Flory equation, and, in some special cases, by means of a uniqueness result for solutions of this equation, prove a weak law of large numbers. This multi-type Flory equation is associated with conserved quantities associated with the process, which may encode different information to conservation of mass (for example, conservation of centre of mass in spatial models). We also apply criteria for gelation in this process to derive sufficient criteria for this equation to exhibit gelling solutions. When this occurs, this multi-type Flory equation encodes, via the associated conserved property, the interaction between the gel and the finite size sol particles. -
D. Heydecker , R.I.A. Patterson, Kac interaction clusters: A bilinear coagulation equation and phase transition, Preprint no. arXiv:1902.07686, Cornell University Library, 2019.
Abstract
We consider the interaction clusters for Kac's model of a gas with quadratic interaction rates, and show that they behave as coagulating particles with a bilinear coagulation kernel. In the large particle number limit the distribution of the interaction cluster sizes is shown to follow an equation of Smoluchowski type. Using a coupling to random graphs, we analyse the limiting equation, showing well-posedness, and a closed form for the time of the gelation phase transition tg when a macroscopic cluster suddenly emerges. We further prove that the second moment of the cluster size distribution diverges exactly at tg. Our methods apply immediately to coagulating particle systems with other bilinear coagulation kernels. -
W.J. Menz, R.I.A. Patterson, W. Wagner, M. Kraft, Application of stochastic weighted algorithms to a multidimensional silica particle model, Preprint no. 120, University of Cambridge, Cambridge Center for Computational Chemical Engineering, 2012.
-
A. Braumann, M. Kraft, W. Wagner, Numerical study of a stochastic particle algorithm solving a multidimensional population balance model for high shear granulation, Technical report no. 93, c4e-Preprint Series, Cambridge Centre for Computational Chemical Engineering, University of Cambridge, Department of Chemical Engineering, 2010.
Abstract
This paper is concerned with computational aspects of a multi-dimensional population balance model of a wet granulation process. Wet granulation is a manufacturing method to form composite particles, granules, from small particles and binders. A detailed numerical study of a stochastic particle algorithm for the solution of a five-dimensional population balance model for wet granulation is presented. Each particle consists of two types of solids (containing pores) and of external and internal liquid (located in the pores). Several transformations of particles are considered, including coalescence, compaction and breakage. A convergence study is performed with respect to the parameter that determines the number of numerical particles. Averaged properties of the system are computed. In addition, the ensemble is subdivided into practically relevant size classes and analysed with respect to the amount of mass and the particle porosity in each class. These results illustrate the importance of the multi-dimensional approach. Finally, the kinetic equation corresponding to the stochastic model is discussed. -
M.S. Celnik, R.I.A. Patterson, M. Kraft, W. Wagner, A predictor-corrector algorithm for the coupling of stiff ODEs to a particle population balance, Preprint no. 58, Cambridge Center for Computational Chemical Engineering, 2008.
Abstract
In this paper a novel predictor-corrector algorithm is presented for the solution of coupled gas-phase---particulate systems. The emphasis of this work is the study of soot formation, but the concepts can be applied to other systems. This algorithm couples a stiff ODE solver to a Monte Carlo population balance solver. Such coupling has been achieved previously for similar systems using a Strang operator splitting algorithm, however, that algorithm demonstrated several numerical issues which resulted in a high computational cost to acquire adequate precision. In particular a source-sink instability was identified whereby a large-magnitude source term present in the ODE system was competing with a similarly sized sink term in the population balance. This instability required that the splitting-step size was very small in order to keep numerical error sufficiently low. A predictor-corrector algorithm has been formulated to negate this instability. An additional efficiency is gained with this algorithm as a principal computational cost of the Strang splitting algorithm is removed: the requirement to re-initialise the ODE solver every splitting-step. The numerical convergence of the new algorithm is demonstrated, and its efficiency is compared to that of the Strang splitting algorithm. Substantial computation time savings are demonstrated, which allow a fixed error in three studied system functionals to be achieved with an order-of-magnitude reduction in computation time.


