This group existed from 2009 to 2016. It was led by Dorothee Knees (until 2014) and Christiane Kraus.
The group focussed on the modeling, analysis and simulation of damage processes. It emerged from a successful application in the Leibniz competition.
Former Members:
Gonca Aki, Jan Giesselmann, Jens André Griepentrog, Hauke Hanke, Christian Heinemann, Rüdiger Müller, Markus Radszuweit, Sina Reichelt, Arne Roggensack
Overview
Damage processes in elastic materials are complex phenomena, which evolve on multiple temporal and spatial scales. Various interacting physical phenomena have to be considered for its understanding. This leads to highly nonlinear and non-smooth coupled, time-dependent systems of partial differential equations. The treatment of those systems in the framework of phase field models requires the development of new analytical tools and adequate numerical algorithms. Thermodynamic consistency played an important role within the approach.A main feature of damage processes is that they are usually unidirectional, in simple terms, the material cannot heal itself. This imposes certain irreversibility constraints on the evolution equations, which are challenging both from the analytical and numerical point of view. In our group we focus on the phase field modeling approach, where sharp (crack) interfaces are approximated by smooth transitions with an order parameter (that is called the damage variable) ranging from fully intact states to completely damaged states. Phase field models can be used to describe the density evolution of micro defects (mean-field approach) as well as to approximate classical (not averaged) fracture phenomena. The evolution of this damage variable can be elegantly described by variational inequalities. Phase field models have recently attracted much attention in fracture mechanics since they are able to predict crack evolution in very general situations without the use of additional criteria and allow to account for crack nucleation, branching and deflection.
Former Research Projects
1. Questions about existence and smoothness properties of solutions for damage models coupled with:- Electrochemical reactions as, for instance, observed in Li-ion batteries
- Phase separation phenomena that occur in solder alloys
- Heat conduction and thermal expansion
- Heterogeneities and phase separation
- Thermomechanics and heat conduction
- Anisotropy
Highlights
Numerical Simulations
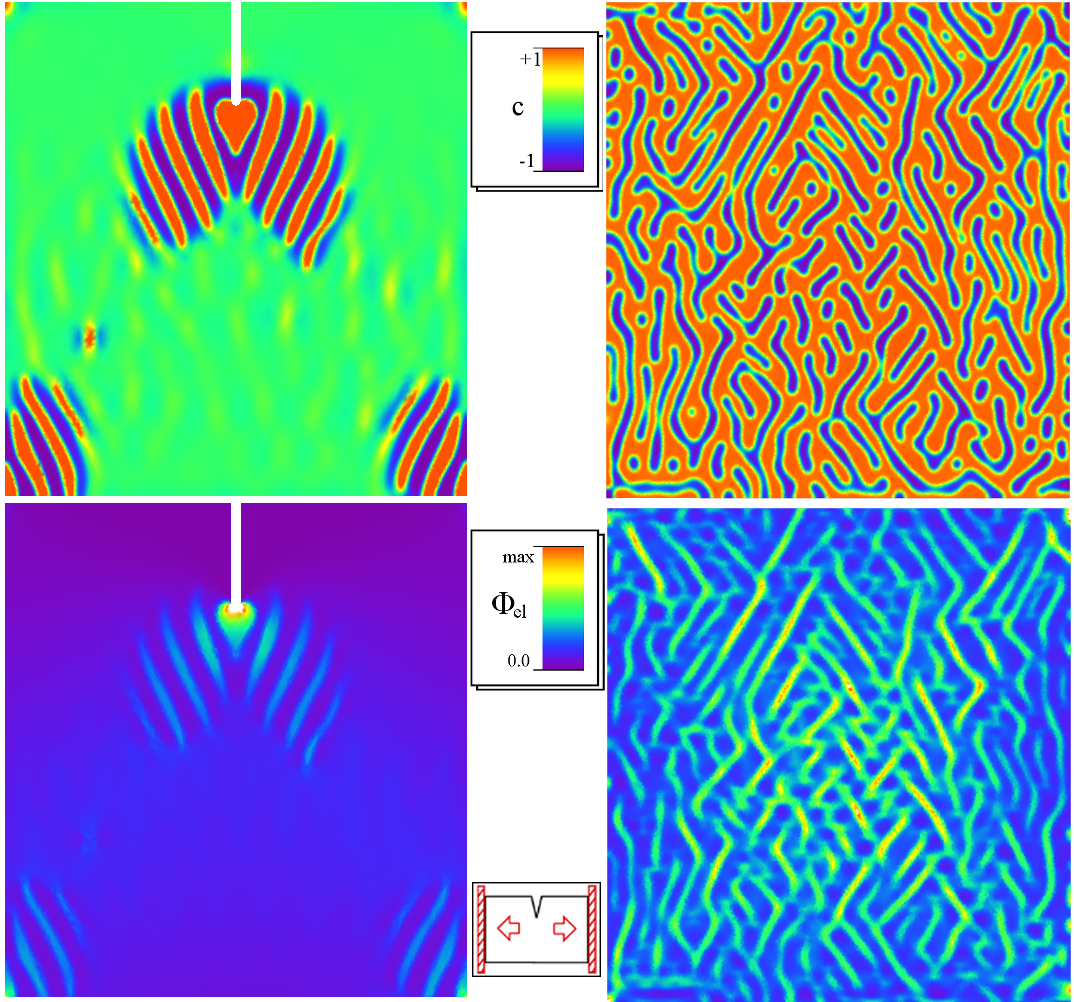 | 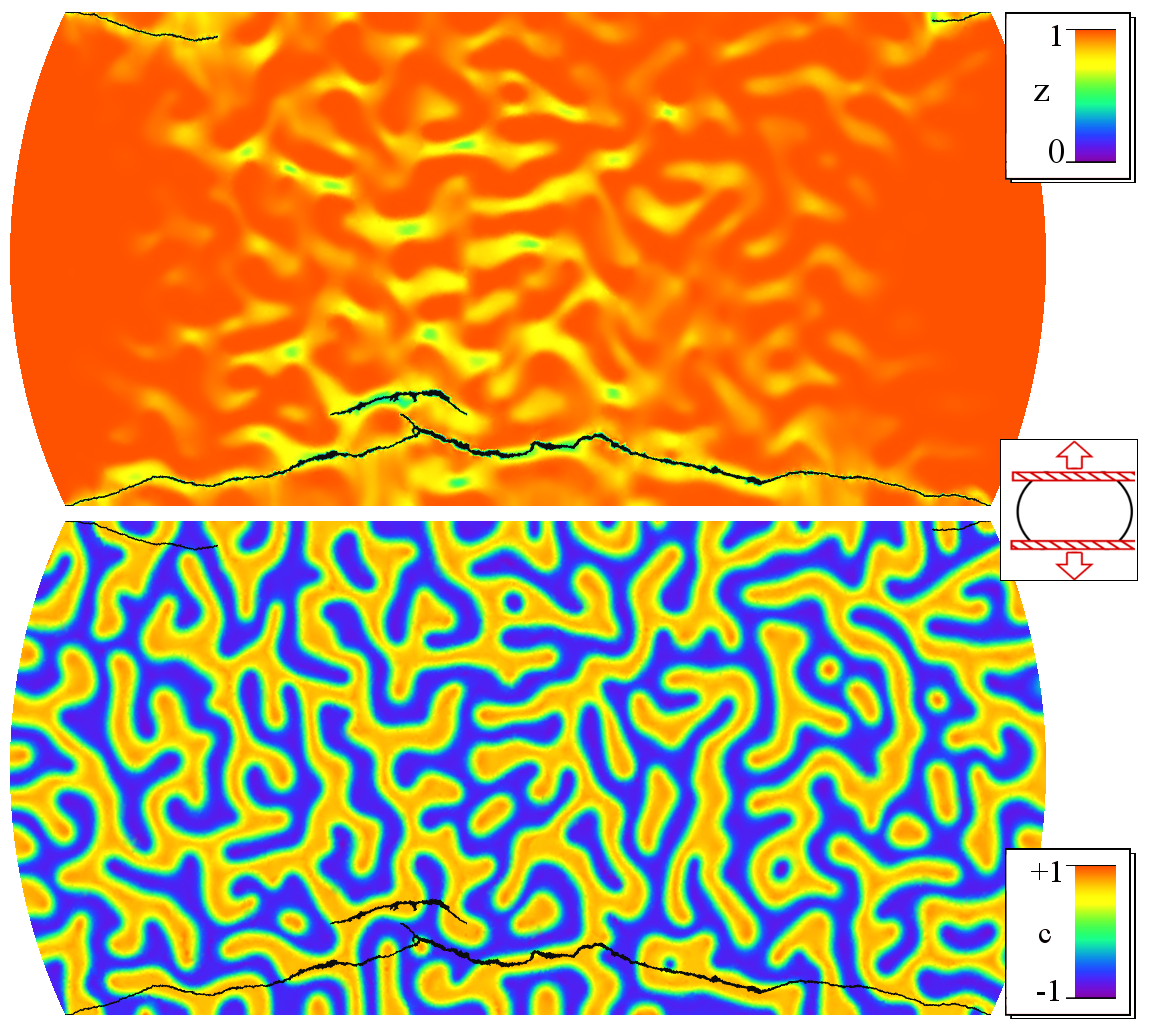 | ||
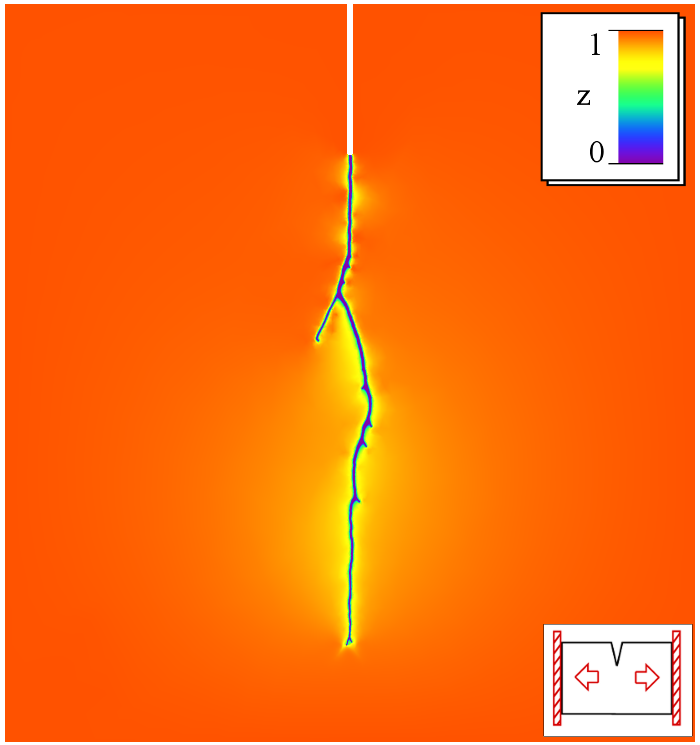 | 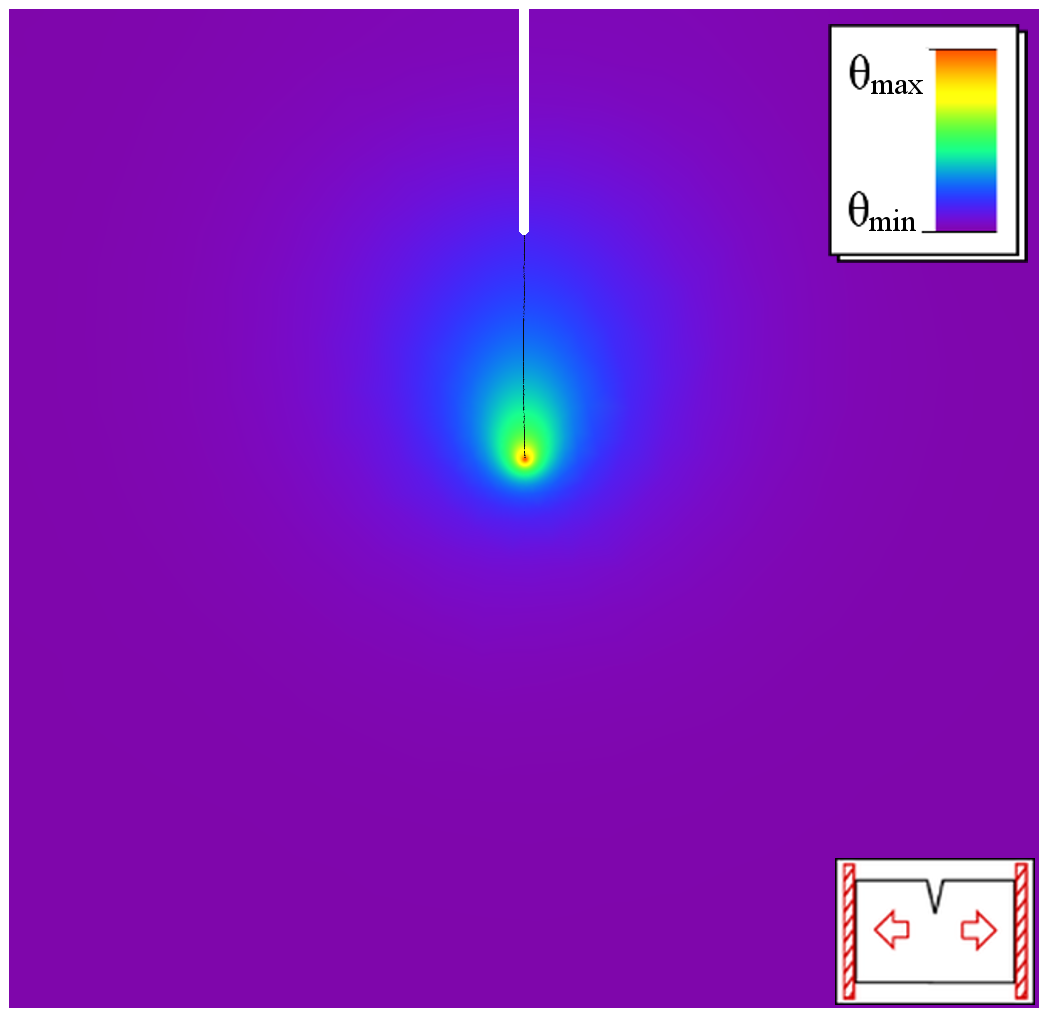 |
Monographs and Dissertations
Ch. Heinemann, Ch. Kraus, Phase Separation Coupled with Damage Processes: Analysis of Phase Field Models in Elastic Media, Springer Fachmedien, Wiesbaden, 2014, 173 pages.
AbstractH. Hanke, Rigorous Derivation of Two-scale and Effective Damage Models Based on Microstructure Evolution, Dissertation, Humboldt-Universität zu Berlin, Mathematisch-Naturwissenschaftliche Fakultät , 2014, 164 pages.
Abstract

