This topic is currently not treated at the WIAS.
In order to produce semiconductor components used in computers, mobile phones, laser devices or solar cells, semiconductor (single- and poly-) crystals of high quality are needed. The growth process of such crystals is complex and quite often expensive. It is important to find strategies to reduce the costs of the growth process and to improve the quality of the produced crystals. In this context electromagnetic fields often play an essential role.Applied mathematics, in particular the techniques of modeling, analysis, and simulation, is used to support the development of growth processes. Their modeling leads to systems of partial differential equations (PDEs) consisting of the following components:
- Maxwell's equations to describe the electromagnetic fields
- (nonlinear) heat equation with nonlocal radiation boundary conditions,
- Navier-Stokes equations in the Boussinesq approximation
- In the framework of the project C9 (2002-2014) of the DFG research center Matheon existence and uniqueness of solutions to the above system of PDEs has been proved. Moreover, optimal control problems have been studied.
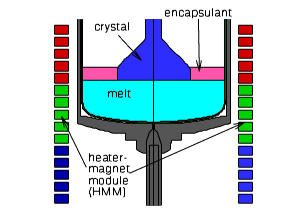
- Within the interdisciplinary project "Kristallzüchtung im Magnetfeld - KirstMAG® (Crystal Growth in Magnetic Fields)" (2005-2008) the use of traveling magnetic field generated by special heater-magnet modules (HMM) has been investigated. Those HMM consists of coils placed above each other (see figure below) replacing the usual meander formed resistance heater units inside the pressure chamber of the growth device. LEC crystal growth processes as well as processes according to the vapour-pressure-controlled Czochralski - VCz strategy have been investigated. The simulations reveal the stabilizing influence of the Lorentz force on the melt. This fact improves the quality of the grown semiconductor single crystals.
- Within the project "Anlagen- und Verfahrensentwicklung sowie Absatz einer neuen Technologie zur Kristallisation von Solar-Silizium, AVANTSolar, (Equipment and process development as well as sale of a new technology for the crystallization of solar silicon)" (2008-2011) is has been studied how time dependent magnetic magnetic fields can be used to improve the yield during the production of multi-crystalline solar silicon. To this end the evolution of impurities within the melt has been studied. Moreover, effects near the triple line where the interface between melt and crystal meets the crucible wall have been considered. Finally, global simulations of temperature and magnetic field within the overall growth apparatus have been performed.
Publications
 Articles in Refereed Journals
Articles in Refereed Journals
-
P. Nestler, N. Schlömer, O. Klein, J. Sprekels, F. Tröltzsch, Optimal control of semiconductor melts by traveling magnetic fields, Vietnam Journal of Mathematics, 47 (2019), pp. 793--812, DOI 10.1007/s10013-019-00355-5 .
Abstract
In this paper, the optimal control of traveling magnetic fields in a process of crystal growth from the melt of semiconductor materials is considered. As controls, the phase shifts of the voltage in the coils of a heater-magnet module are employed to generate Lorentz forces for stirring the crystal melt in an optimal way. By the use of a new industrial heater-magnet module, the Lorentz forces have a stronger impact on the melt than in earlier technologies. It is known from experiments that during the growth process temperature oscillations with respect to time occur in the neighborhood of the solid-liquid interface. These oscillations may strongly influence the quality of the growing single crystal. As it seems to be impossible to suppress them completely, the main goal of optimization has to be less ambitious, namely, one tries to achieve oscillations that have a small amplitude and a frequency which is sufficiently high such that the solid-liquid interface does not have enough time to react to the oscillations. In our approach, we control the oscillations at a finite number of selected points in the neighborhood of the solidification front. The system dynamics is modeled by a coupled system of partial differential equations that account for instationary heat condution, turbulent melt flow, and magnetic field. We report on numerical methods for solving this system and for the optimization of the whole process. Different objective functionals are tested to reach the goal of optimization. -
P.-É. Druet, Higher $L^p$ regularity for vector fields that satisfy divergence and rotation constraints in dual Sobolev spaces, and application to some low-frequency Maxwell equations, Discrete and Continuous Dynamical Systems, 8 (2015), pp. 479--496.
Abstract
We show that Lp vector fields over a Lipschitz domain are integrable to higher exponents if their generalized divergence and rotation can be identified with bounded linear operators acting on standard Sobolev spaces. A Div-Curl Lemma-type argument provides compact embedding results for such vector fields. We investigate the regularity of the solution fields for the low-frequency approximation of the Maxwell equations in time-harmonic regime. We focus on the weak formulation 'in H' of the problem, in a reference geometrical setting allowing for material heterogeneities. -
P.-É. Druet, Some mathematical problems related to the second order optimal shape of a crystallization interface, Discrete and Continuous Dynamical Systems, 35 (2015), pp. 2443--2463.
Abstract
We consider the problem to optimize the stationary temperature distribution and the equilibrium shape of the solid-liquid interface in a two-phase system subject to a temperature gradient. The interface satisfies the minimization principle of the free energy, while the temperature is solving the heat equation with a radiation boundary conditions at the outer wall. Under the condition that the temperature gradient is uniformly negative in the direction of crystallization, the interface is expected to have a global graph representation. We reformulate this condition as a pointwise constraint on the gradient of the state, and we derive the first order optimality system for a class of objective functionals that account for the second surface derivatives, and for the surface temperature gradient. -
CH. Kudla, A.T. Blumenau, F. Büllesfeld, N. Dropka, Ch. Frank-Rotsch, F. Kiessling, O. Klein, P. Lange, W. Miller, U. Rehse, U. Sahr, M. Schellhorn, G. Weidemann, M. Ziem, G. Bethin, R. Fornari, M. Müller, J. Sprekels, V. Trautmann, P. Rudolph, Crystallization of 640 kg mc-silicon ingots under traveling magnetic field by using a heater-magnet module, Journal of Crystal Growth, 365 (2013), pp. 54--58.
-
P.-E. Druet, The classical solvability of the contact angle problem for generalized equations of mean curvature type, Portugaliae Mathematica. A Journal of the Portuguese Mathematical Society, 69 (2012), pp. 233--258.
Abstract
In this paper, mean curvature type equations with general potentials and contact angle boundary conditions are considered. We extend the ideas of Ural'tseva, formulating sharper hypotheses for the existence of a classical solution. Corner stone for these results is a method to estimate quantities on the boundary of the free surface. We moreover provide alternative proofs for the higher-order estimates, and for the existence result. -
W. Dreyer, P.-É. Druet, O. Klein, J. Sprekels, Mathematical modeling of Czochralski type growth processes for semiconductor bulk single crystals, Milan Journal of Mathematics, 80 (2012), pp. 311--332.
Abstract
This paper deals with the mathematical modeling and simulation of crystal growth processes by the so-called Czochralski method and related methods, which are important industrial processes to grow large bulk single crystals of semiconductor materials such as, e.,g., gallium arsenide (GaAs) or silicon (Si) from the melt. In particular, we investigate a recently developed technology in which traveling magnetic fields are applied in order to control the behavior of the turbulent melt flow. Since numerous different physical effects like electromagnetic fields, turbulent melt flows, high temperatures, heat transfer via radiation, etc., play an important role in the process, the corresponding mathematical model leads to an extremely difficult system of initial-boundary value problems for nonlinearly coupled partial differential equations. In this paper, we describe a mathematical model that is under use for the simulation of real-life growth scenarios, and we give an overview of mathematical results and numerical simulations that have been obtained for it in recent years. -
P.-E. Druet, P. Philip, Noncompactness of integral operators modeling diffuse-gray radiation in polyhedral and transient settings, Integral Equations and Operator Theory, 69 (2011), pp. 101--111.
-
P.-É. Druet, O. Klein, J. Sprekels, F. Tröltzsch, I. Yousept, Optimal control of three-dimensional state-constrained induction heating problems with nonlocal radiation effects, SIAM Journal on Control and Optimization, 49 (2011), pp. 1707--1736.
Abstract
The paper is concerned with a class of optimal heating problems in semiconductor single crystal growth processes. To model the heating process, time-harmonic Maxwell equations are considered in the system of the state. Due to the high temperatures characterizing crystal growth, it is necessary to include nonlocal radiation boundary conditions and a temperature-dependent heat conductivity in the description of the heat transfer process. The first goal of this paper is to prove the existence and uniqueness of the solution to the state equation. The regularity analysis associated with the time harmonic Maxwell equations is also studied. In the second part of the paper, the existence and uniqueness of the solution to the corresponding linearized equation is shown. With this result at hand, the differentiability of the control-to-state mapping operator associated with the state equation is derived. Finally, based on the theoretical results, first oder necessary optimality conditions for an associated optimal control problem are established. -
P.-É. Druet, Weak solutions to a time-dependent heat equation with nonlocal radiation boundary condition and arbitrary $p$-summable right-hand side, Applications of Mathematics, 55 (2010), pp. 111--149.
Abstract
It is known that the time-dependent heat equation with nonlocal radiation boundary conditions possesses a unique weak solution if the heat sources are in L-2. In this paper, we generalize the known existence and uniqueness results to the case that the right-hand side belongs to an arbitrary L-p space (p >= 1). This is the continuation of the results that we recently proved for the stationary problem. The purpose of both papers is to obtain energy estimates that involve only the L-p norm of the heat sources for some exponent p close to one. Such estimates are important for the investigation of models in which the heat equation is coupled to Maxwell's equations or to the Navier-Stokes equations (dissipative heating). -
P.-É. Druet, Existence for the stationary MHD equations coupled to heat transfer with nonlocal radiation effects, Czechoslovak Mathematical Journal, 59 (2009), pp. 791--825.
-
P.-É. Druet, Existence of weak solution to time-dependent MHD equations coupled to heat transfer with nonlocal radiation boundary conditions, Nonlinear Analysis. Real World Applications. An International Multidisciplinary Journal, 10 (2009), pp. 2914--2936.
-
P. Rudolph, M. Czupalla, N. Dropka, Ch. Frank-Rotsch, F.-M. Kiessling, O. Klein, B. Lux, W. Miller, U. Rehse, O. Root, Crystal growth from melt in combined heater-magnet modules, Journal of the Korean Crystal Growth and Crystal Technology, 19 (2009), pp. 215-222.
-
O. Klein, Ch. Lechner, P.-É. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F.M. Kiessling, W. Miller, U. Rehse, P. Rudolph, Numerical simulations of the influence of a traveling magnetic field, generated by an internal heater-magnet module, on liquid encapsulated Czochralski crystal growth, Magnetohydrodynamics. Consultants Bureau, New York (US). Consultants Bureau, New York. Translation from: Magnitnaya Gidrodinamika., 45 (2009), pp. 557-567.
-
P.-É. Druet, Weak solutions to a stationary heat equation with nonlocal radiation boundary condition and right-hand side in $L^p$ with $pge 1$, Mathematical Methods in the Applied Sciences, 32 (2008), pp. 135--166.
Abstract
Accurate modeling of heat transfer in high-temperatures situations requires to account for the effect of heat radiation. In complex applications such as Czochralski's method for crystal growth, in which the conduction radiation heat transfer problem couples to an induction heating problem and to the melt flow problem, we hardly can expect from the mathematical theory that the heat sources will be in a better space than L-1. In such situations, the known results on the unique solvability of the heat conduction problem with surface radiation do not apply, since a right-hand side in L-p with p < 6/5 no longer belongs to the dual of the Banach space in which coercivity is obtained. In this paper, we focus on a stationary heat equation with non-local boundary conditions and right-hand side in L-p with p>=1 arbitrary. Essentially, we construct an approximation procedure and, thanks to new coercivity results, we are able to produce energy estimates that involve only the L-p-norm of the heat-sources, and to pass to the limit. -
J. Geiser, O. Klein, P. Philip, A finite volume scheme designed for anisotropic heat transfer in general polyhedral domains, Advances in Mathematical Sciences and Applications, 18 (2008), pp. 43--67.
-
O. Klein, Ch. Lechner, P.-É. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F.M. Kiessling, W. Miller, U. Rehse, P. Rudolph, Numerical simulation of Czochralski crystal growth under the influence of a traveling magnetic field generated by an internal heater-magnet module (HMM), Journal of Crystal Growth, 310 (2008), pp. 1523-1532.
-
CH. Lechner, O. Klein, P.-É. Druet, Development of a software for the numerical simulation of VCz growth under the influence of a traveling magnetic field, Journal of Crystal Growth, 303 (2007), pp. 161-164.
-
J. Geiser, O. Klein, P. Philip, Numerical simulation of temperature fields during the sublimation growth of SiC single crystals, using WIAS-HiTNIHS, Journal of Crystal Growth, 303 (2007), pp. 352-356.
-
J. Geiser, O. Klein, P. Philip, Influence of anisotropic thermal conductivity in the apparatus insulation for sublimation growth of SiC: Numerical investigation of heat transfer, Crystal Growth & Design, 6 (2006), pp. 2021--2028.
-
J. Geiser, O. Klein, P. Philip, Transient numerical study of temperature gradients during sublimation growth of SiC: Dependence on apparatus design, Journal of Crystal Growth, 297 (2006), pp. 20-32.
-
P. Philip, O. Klein, Transient conductive-radiative heat transfer: Discrete existence and uniqueness for a finite volume scheme, Mathematical Models & Methods in Applied Sciences, 15 (2005), pp. 227--258.
-
O. Klein, P. Philip, J. Sprekels, Modeling and simulation of sublimation growth of SiC bulk single crystals, Interfaces and Free Boundaries. Mathematical Analysis, Computation and Applications, 6 (2004), pp. 295--314.
-
O. Klein, P. Philip, Transient numerical investigation of induction heating during sublimation growth of silicon carbide single crystals, Journal of Crystal Growth, 247 (2003), pp. 219--235.
-
O. Klein, P. Philip, Transient temperature phenomena during sublimation growth of silicon carbide single crystals, Journal of Crystal Growth, 249 (2003), pp. 514--522.
-
O. Klein, P. Philip, J. Sprekels, K. Wilmanski, Radiation- and convection-driven transient heat transfer during sublimation growth of silicon carbide single crystals, Journal of Crystal Growth, 222 (2001), pp. 832--851.
 Contributions to Collected Editions
Contributions to Collected Editions
-
M. Hintermüller, D. Hömberg, O. Klein, J. Sprekels, F. Tröltzsch, C4 -- PDE-constrained optimization with industrial applications, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 207--222.
-
O. Klein, J. Sprekels, SHOWCASE 13 -- Growth of semiconductor bulk single crystals, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 224--225.
-
N. Dropka, W. Miller, U. Rehse, P. Rudolph, F. Bullesfeld, U. Sahr, O. Klein, D. Reinhardt, Numerical study on improved mixing in silicon melts by double-frequency TMF, in: Proceedings of the 16th International Conference on Crystal Growth (ICCG-16), J. Crystal Growth, 318, 2011, pp. 275--279.
-
P.-É. Druet, Weak solutions to a model for crystal growth from the melt in changing magnetic fields, in: Optimal Control of Coupled Systems of Partial Differential Equations, K. Kunisch, G. Leugering, J. Sprekels, F. Tröltzsch, eds., 158 of Internat. Series Numer. Math., Birkhäuser, Basel et al., 2009, pp. 123--137.
-
P. Rudolph, Ch. Frank-Rotsch, F.-M. Kiessling, W. Miller, U. Rehse, O. Klein, Ch. Lechner, J. Sprekels, B. Nacke, H. Kasjanov, P. Lange, M. Ziem, B. Lux, M. Czupalla, O. Root, V. Trautmann, G. Bethin, Crystal growth in heater-magnet modules --- From concept to use, in: Proceedings of the International Scientific Colloquium Modelling for Electromagnetic Processing (MEP2008), Hannover, October 26--29, 2008, E. Braake, B. Nacke, eds., Leibniz University of Hannover, 2008, pp. 79-84.
-
P.-É. Druet, Weak solutions to a model for global heat transfer arising in crystal growth from the melt with applied magnetic fields, in: Optimal Control of Coupled Systems of PDE, Workshop, March 2--8, 2008, 5 of Oberwolfach Reports, Mathematisches Forschungsinstitut Oberwolfach, 2008, pp. 597--599.
-
O. Klein, P.-É. Druet, J. Sprekels, Ch. Lechner, P. Philip, Ch. Frank-Rotsch, F.-M. Kiessling, W. Miller, U. Rehse, P. Rudolph, Numerical simulations of the influence of a traveling magnetic field, generated by an internal heater magnetic module, on Czochralski crystal growth, in: Proceedings of the International Scientific Colloquium Modelling for Electromagnetic Processing (MEP2008), Hannover, October 26--29, 2008, E. Braake, B. Nacke, eds., Leibniz University of Hannover, 2008, pp. 91-96.
-
J. Geiser, O. Klein, P. Philip, tt WIAS-HiTNIHS: Software tool for simulation in crystal growth for SiC single crystal: Application and methods, in: Proceedings of ``International Congress of Nanotechnology'', San Francisco, USA, November 7 -- 10, 2004, 2005.
-
J. Sprekels, O. Klein, P. Philip, K. Wilmanski, Optimal control of sublimation growth of SiC crystals, in: Mathematics --- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.-J. Krebs, eds., Springer, Berlin [u.a.], 2003, pp. 334--343.
 Talks, Poster
Talks, Poster
-
P.-E. Druet, On the heat equation coupled to a mean curvature type equation, Seminar ``Dünne Filme und freie Randwertprobleme'', Technische Universität Berlin, June 19, 2014.
-
P.-E. Druet, Optimization of crystal growth using magnetic fields: Some mathematical aspects, The 18th European Conference on Mathematics for Industry 2014 (ECMI 2014), Minisymposium 36: Recent Trends in Modeling, Analysis, and Simulation of Induction Heat Treatments, June 9 - 14, 2014, Taormina, Italy, June 13, 2014.
-
P.-E. Druet, Some results on distributional solvability vs. higher regularity of the fields in low-frequency electromagnetics, IFIP TC7.2 Workshop Electromagnetics -- Modelling, Simulation, Control and Industrial Applications, May 13 - 17, 2013, WIAS, Berlin, May 13, 2013.
-
P.-E. Druet, On the convexification of functionals associated with the mean-curvature equation, 12th International Conference on Free Boundary Problems: Theory and Applications, June 11 - 15, 2012, Frauenchiemsee, June 13, 2012.
-
P.-É. Druet, Some problems associated with the second order optimal shape of a crystallisation interface, PDEs for multiphase advanced materials, ADMAT2012, September 17 - 21, 2012, Cortona, Italy, September 20, 2012.
-
O. Klein, Modeling and numerical simulation of the application of traveling magneticfields to stabilize crystal growth from the melt, 12th International Conference on Free Boundary Problems: Theory and Applications, June 11 - 15, 2012, Frauenchiemsee, June 11, 2012.
-
J. Sprekels, Mathematical challenges in the industrial growth of semiconductor bulk single crystals, Kick-off Symposium Mathematics: Official Opening of the Felix Klein Building, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, January 13, 2012.
-
J. Sprekels, Optimal control problems arising in the industrial growth of bulk semiconductor single crystals, 21st International Symposium on Mathematical Programming (ISMP), Invited Session ``Optimization Applications in Industry I'', August 19 - 24, 2012, Technische Universität Berlin, August 21, 2012.
-
J. Sprekels, Optimal control problems arising in the industrial growth of bulk single semiconductor crystals, Applied Mathematics Seminar, Università di Pavia, Dipartimento di Matematica ``F. Casorati'', Italy, September 11, 2012.
-
P.-E. Druet, On existence and regularity results for the equations of magnetohydrodynamics in complex geometries, Seminar of International Research Training Group 1529 ``Mathematical Fluid Dynamics'', Technische Universität Darmstadt, June 14, 2011.
-
J. Sprekels, Mathematical challenges in the industrial growth of semiconductor bulk single crystals, Multiphase and Multiphysics Problems, September 25 - 30, 2011, Riemann International School of Mathematics, Verbania, Italy, September 26, 2011.
-
J. Sprekels, Real-life crystal growth: Turbulence, magnetic fields, heat transfer via radiation, and free boundaries, Interfaces and Discontinuities in Solids, Liquids and Crystals (INDI2011), Special Session: Between Mechanics and Mathematics: The ``Non-smooth'' View by Michel Frémond, June 20 - 23, 2011, Gargnano (Brescia), Italy, June 21, 2011.
-
J. Sprekels, Technological and mathematical problems in the industrial growth of semiconductor bulk single crystals, Workshop ``Nonlinear Diffusion: Algorithms, Analysis and Applications'', June 6 - 8, 2011, Warwick Mathematics Institute, UK, June 7, 2011.
-
J. Sprekels, Technological and mathematical problems in the industrial growth of semiconductor bulk single crystals, Academy of Sciences of the Czech Republic, Institute of Mathematics, Prague, March 15, 2011.
-
K. Afanasiev, F. Duderstadt, W. Dreyer, S. Eichler, O. Klein, J. Sprekels, On effects in the vicinity of the solid melt interface during GaAs crystal growth from the melt, Status Seminar AVANTem SOLAR, Griebnitzsee, September 9 - 10, 2010.
-
W. Dreyer, P.-É. Druet, F. Duderstadt, Ch. Grützmacher, O. Klein, D. Reinhardt, J. Sprekels, Ch. Frank-Rotsch, F.-M. Kiessling, W. Miller, U. Rehse, P. Rudolph, Ch. Lechner, Crystal growth under the influence of traveling magnetic fields, Status Seminar AVANTem SOLAR, Griebnitzsee, September 9 - 10, 2010.
-
O. Klein, K. Afanasiev, F. Duderstadt, W. Dreyer, S. Eichler, J. Sprekels, On effects in the vicinity of the solid melt interface during crystal growth from the melt, The 16th International Conference on Crystal Growth (ICCG-16) in conjunction with The 14th International Conference on Vapor Growth and Epitaxy (ICVGE-14), Beijing, China, August 8 - 13, 2010.
-
O. Klein, Modeling and simulations for directional solidification of solar-grade silicon under the influence of traveling magnetic fields, The 16th International Conference on Crystal Growth (ICCG-16) in conjunction with The 14th International Conference on Vapor Growth and Epitaxy( ICVGE-14), August 8 - 13, 2010, Beijing, China, August 10, 2010.
-
O. Klein, Numerical simulation of the use of traveling magnetic fields to stabilize crystal growth from the melt, Warsaw Seminar on Industrial Mathematics (WSIM'10), March 18 - 19, 2010, Warsaw University of Technology, Poland, March 18, 2010.
-
J. Sprekels, Mathematical problems in industrial crystal growth: Radiation, magnetic fields, and free boundaries, Symposium zur Angewandten Mathematik (zum 100. Geburtstag von Lothar Collatz), October 7 - 8, 2010, Universität Hamburg, October 7, 2010.
-
J. Sprekels, Praktische und mathematische Probleme bei der Züchtung von Halbleiter-Einkristallen, Technische Universität Chemnitz, Forschungsseminar Numerik, January 5, 2010.
-
J. Sprekels, Technical and mathematical problems in the Czochralski growth of single crystals, Workshop ``New Directions in Simulation, Control and Analysis for Interfaces and Free Boundaries'', January 31 - February 6, 2010, Mathematisches Forschungsinstitut Oberwolfach, February 1, 2010.
-
P.-É. Druet, Higher integrability of the magnetic field for 3D induction heating and MHD problems, 14th Belgian-French-German Conference on Optimization, September 14 - 18, 2009, Leuven, Belgium, September 15, 2009.
-
O. Klein, Modulierung und Simulation der LEC GaAs Züchtung in Heizer-Magnetmodulen, 10. Kinetikseminar & 6. Workshop Angewandte Simulation in der Kristallzüchtung, April 1 - 3, 2009, Deutsche Gesellschaft für Kristallwachstum und Kristallzüchtung e.V., Griebnitzsee, April 2, 2009.
-
O. Klein, Numerical simulation of Czochralski crystal growth stabilized by a traveling magnetic field generated by an internal heater-magnet module (HMM), EUROTHERM 84 - ``Thermodynamics of Phase Changes'', May 25 - 27, 2009, Université Catholique de Louvain, Namur, Belgium, May 25, 2009.
-
J. Sprekels, Problems in the industrial growth of semiconductor crystals: Radiative transfer, convection, magnetic fields, and free boundaries, Seminar of the Institute of Applied Mathematics and Information Technology, Università di Pavia, Dipartimento di Matematica ``F. Casorati'', Italy, September 23, 2009.
-
J. Sprekels, Problems in the industrial growth of semiconductor crystals: Radiative transfer, convection, magnetic fields, and free boundaries, BMS Days 2009, Berlin Mathematical School, Urania Berlin, February 17, 2009.
-
P.-É. Druet, Weak solutions to a model for global heat transfer arising in crystal growth from the melt with applied magnetic fields, Workshop ``Optimal Control of Coupled Systems'', March 2 - 7, 2008, Mathematisches Forschungsinstitut Oberwolfach, March 5, 2008.
-
P.-É. Druet, On weak solutions to the system of magnetohydrodynamics coupled to heat transfer, including nonlocal radiation effects, Oberseminar Analysis, Technische Universität Dresden, Institut für Analysis, January 31, 2008.
-
O. Klein, Numerical simulations of the influenece of a traveling magnetic field, generated by an internal heater magnetic module, on Czochralski crystal growth, International Scientific Colloquium ``Modelling for Electromagnetic Processing'' (MEP 2008), October 26 - 29, 2008, Leibniz Universität Hannover, Hannover, October 27, 2008.
-
J. Sprekels, Problems in the industrial growth of semiconductor crystals: Radiative heat transfer, convection, magnetic fields and free boundaries, The Legacy of John Crank -- Developments in Time Dependent PDE's, Diffusion and Free Boundary Problems, July 9 - 11, 2008, Brunel University, Uxbridge, UK, July 10, 2008.
-
O. Klein, Ch. Lechner, P.-É. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F.-M. Kiessling, W. Miller, U. Rehse, P. Rudolph, Numerical simulation of Czochralski crystal growth under the influence of a traveling magnetic field generated by an internal heater-magnet module (HMM), The 15th International Conference on Crystal Growth, Salt Lake City, USA, August 12 - 17, 2007.
-
O. Klein, P. Philip, J. Geiser, D. Siche, J. Wollweber, Numerical investigation of the influence of an anisotropic insulation felt on the temperature field in a PVT growth apparatus, The 15th International Conference on Crystal Growth, Salt Lake City, USA, August 12 - 17, 2007.
-
J. Geiser, O. Klein, P. Philip, Numerical simulation of temperature fields during the sublimation growth of SiC single crystals using ttfamily WIAS-HiTNIHS, 5th International Workshop on Modeling in Crystal Growth, Bamberg, September 10 - 13, 2006.
-
O. Klein, Ch. Lechner, P.-É. Druet, Numerical simulation of VCz growth with a traveling magnetic field, 5th International Workshop on Modeling in Crystal Growth, Bamberg, September 10 - 13, 2006.
-
O. Klein, Modeling Czochralski crystal growth under the influence of electromagnetic forces, Recent Advances in Free Boundary Problems and Related Topics (FBP2006), September 14 - 16, 2006, Levico, Italy, September 15, 2006.
-
J. Geiser, O. Klein, Numerical simulations of sublimation growth for SiC single crystals: Anisotropy materials, radiation and transient heat-transfer, Eighth U.S. National Congress on Computational Mechanics, Session: Complex Models in Solid and Fluid Mechanics: Methods and Applications in Multi-physical and Multi-scaling Problems (2), July 24 - 28, 2005, U.S. Association for Computational Mechanics, Austin, USA, July 27, 2005.
-
O. Klein, Neue Entwicklungen in der Simulation der Sublimationszüchtung mit WIAS-HiTNIHS: Anisotropie, Semitransparenz, Nutzeroberfläche, DGKK Arbeitskreis Angewandte Simulation in der Kristallzüchtung, November 2 - 4, 2005, Deutsche Gesellschaft für Kristallwachstum und Kristallzüchtung e.V., Heigenbrücken, November 3, 2005.
-
O. Klein, Numerical simulations of sublimation growth for SiC single crystal: Induction heating, anisotropy materials, radiation and Considerations for dealing with several coils within the project KristMag, Treffen der Numeriker-Gruppe des KristMag-Projektes, Universität Hannover, Institut für Elektrothermische Prozesse, September 7, 2005.
-
O. Klein, Optimierung des Temperaturfeldes bei der Sublimationszüchtung von SiC Einkristallen, DGKK Arbeitskreis Angewandte Simulation in der Kristallzüchtung, February 5 - 6, 2004, Deutsche Gesellschaft für Kristallwachstum und Kristallzüchtung e.V., Volkach, February 5, 2004.
-
C. Meyer, O. Klein, P. Philip, A. Rösch, J. Sprekels, F. Tröltzsch, Optimal"-steuerung bei der Herstellung von SiC-Einkristallen, MathInside---Überall ist Mathematik, event of the DFG Research Center ``Mathematics for Key Technologies'' on the occasion of the Open Day of Urania, Berlin, September 13, 2003.
-
O. Klein, P. Philip, J. Sprekels, K. Wilmanski, Numerical simulations and control of SiC bulk single crystal growth, Statusseminar zum BMBF-Fördergebiet "`Ausgewählte Gebiete der Mathematik"', Frankfurt am Main, December 11 - 12, 2000.
Contact
Contributing Groups of WIAS
Mathematical Context
- Algorithms for the generation of 3D boundary conforming Delaunay meshes
- Direct and inverse problems for the Maxwell equations
- Free boundary problems for partial differential equations
- Magnetohydrodynamics
- Numerical methods for problems from fluid dynamics
- Optimal control of partial differential equations and nonlinear optimization
- Systems of partial differential equations: modeling, numerical analysis and simulation