Strömung und Transport von Stoffen sind wichtige Phänomene in vielen Prozessen in Natur und Industrie. Die physikalische Konsistenz von Diskretisierungen ist von großer Bedeutung in vielen Anwendungen. Physikalische Konsistenz bedeutet für parabolische und elliptische (Anfangs-) Randwert-Probleme beispielsweise, dass diskrete Maximumprinzipien erfüllt sind, wie in diesem Übersichtsartikel beschrieben. Für inkompressible Strömungsprobleme sind die Massenerhaltung und die Unabhängigkeit von Geschwindigkeitsfehlern vom Druck, die sogenannte Druckrobustheit, wesentliche Eigenschaften einer physikalisch konsistenten numerischen Lösung, siehe diese in SIAM Review publizierte Arbeit. Andere mehr theoretische Forschungsthemen befassen sich mit konvektions-robusten Diskretisierungen und mit reduzierten Modellen, welche auf Singulärwertzerlegungen beruhen (POD-ROM).
Die untersuchten Diskretisierungen werden in Simulationen für Anwendungen genutzt. Betrachtete Anwendungen sind beispielsweise Probleme aus der Biomedizin und elektrochemische Systeme. Anwendungen innerhalb dieses Hauptanwendungsgebiets bilden aktive Themen und Kooperationsprojekte innerhalb des Leibniz-Forschungsnetzwerk Mathematische Modellierung und Simulation (MMS).
*) D. Janke, A. Caiazzo, N. Ahmed, N. Alia, O. Knoth, B. Moreau, U. Wilbrandt, D. Willink, Th. Amon, V. John, On the feasibility of using open source solvers for the simulation of a turbulent air flow in a dairy barn, Computers and Electronics in Agriculture, 175 (2020), pp. 105546/1--105546/16, DOI 10.1016/j.compag.2020.105546

Thermodynamische Modelle elektrochemischer Systeme
Das Verhalten elektrochemischer Systeme wird auf der Basis von Kontinuumsmodellen untersucht. Solche Modelle lassen sich u.a. auf Gebieten wie Elektrochemie an Einkristalloberflächen, Lithium-Ionen-Batterien, Brennstoffzellen, Nanoporen in biologischen Membranen, Elektrolyse und Korrosion einsetzen.

Phasenfeldmodelle für komplexe Materialien und Grenzflächen
Dieses Forschungsthema behandelt die Modellierung komplexer Materialsysteme mit verschiedenen Phasen, einschließlich Mehrphasen- und Grenzflächenströmungen, Schadens- und Materialermüdungsmodellierung, Topologieoptimierung und komplexe Materialien. Zu den modellierten physikalischen Phänomenen gehören Flüssigkeitsströmung, diffuser Transport und (visko)elastische Deformationsprozesse im Zusammenhang mit Phasentrennung und Phasenübergängen. Die Anwendungen reichen von der Biologie über die Physik bis hin zum Ingenieurwesen.
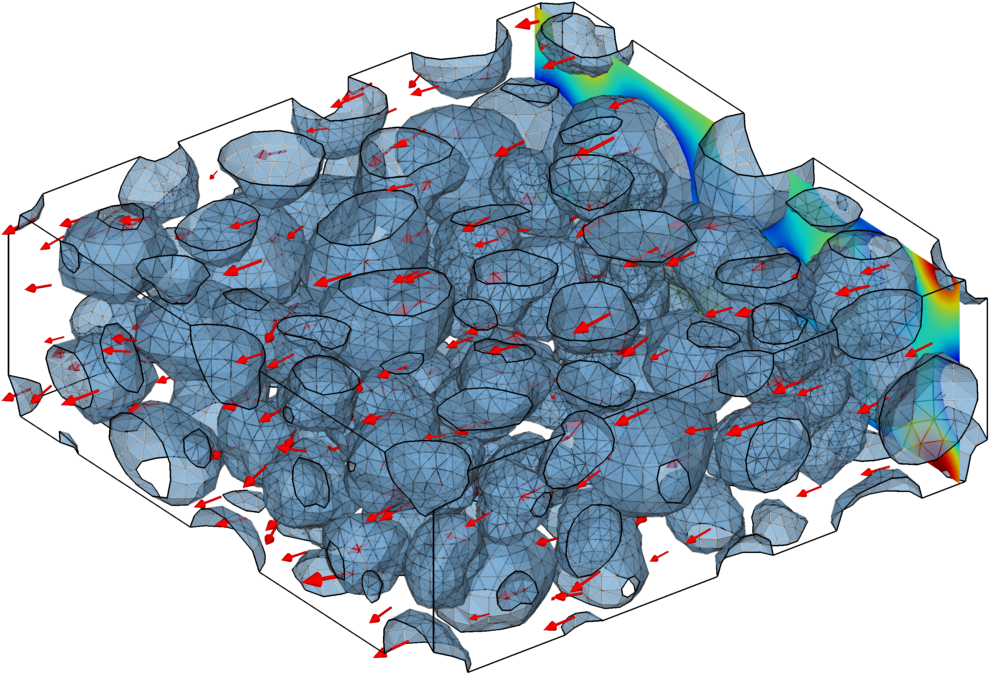
Mathematische Modelle und Methoden für Lithium-Ionen-Batterien
In modernen Lithium-Ionen-Batterien laufen eine Vielzahl von physikochemischen Prozessen parallel auf verschiedenen Größen- und Zeitskalen ab. Um ihren Einfluss sowie ihre Wechselwirkung innerhalb einer Batterie systematisch untersuchen zu können, werden mathematische Modelle entwickelt, die mithilfe von partiellen Differentialgleichungen die entsprechenden Prozesse abbilden. Mithilfe numerischer Methoden können spezifische Kenngrößen einer Batterie berechnet werden, wie zum Beispiel die Zellspannung in Abhängigkeit des Ladezustands. Die Modelle werden kontinuierlich weiterentwickelt, um beispielsweise Alterungseffekte berücksichtigen zu können.

Modellierung, Simulation und Optimierung für Anwendungen in der Biomedizin
In der Medizin werden heute bei der Diagnostik und Therapieplanung digitale Instrumente zur Simulation von Prozessen im menschlichen Körper genutzt. Am WIAS werden Modelle für biologische Gewebe, Fluide und deren Interaktion, sowie Techniken der Optimierung und Steuerung zur Unterstützung von Entscheidungsprozessen in der Biomedizin entwickelt.
Modellierung dünner Filme und Nanostrukturen auf Substraten
Dünne Filme spielen eine wichtige Rolle in der Natur und vielen technologischen Anwendungen. Insbesondere im Mikro- und Nanometerbereich werden zum Beispiel Entnetzungsprozesse oder epitaktisches Wachstum zum Design von Oberflächen mit spezifischen Materialeigenschaften eingesetzt. Neben der Bedeutung, die die mathematische Modellierung, Analysis und numerische Simulation für die Beschleunigung der Entwicklung neuere Technologien hat, ist es auch wissenschsftlich auch äußerst interessant Materialeigenschaften auf diesen kleinen Skalen zu verstehen.
Hauptanwendungsgebiete
Ansprechpartner
Beteiligte Gruppen
- Partielle Differentialgleichungen
- Numerische Mathematik und Wissenschaftliches Rechnen
- Nichtlineare Optimierung und Inverse Probleme
- Stochastische Systeme mit Wechselwirkung
- Thermodynamische Modellierung und Analyse von Phasenübergängen
- Nichtglatte Variationsprobleme und Operatorgleichungen
- Erhaltungssätze und Bilanzgleichungen für Multikomponentensysteme


