Multiscale coupling of one-dimensional vascular models and elastic tissues
Authors
- Heltai, Luca
- Caiazzo, Alfonso
ORCID: 0000-0002-7125-8645 - Müller, Lucas O.
2020 Mathematics Subject Classification
- 74F10 74Q99 74S05 74G15
Keywords
- Vascularized tissues, immersed methods, finite element methods, finite volume methods
DOI
Abstract
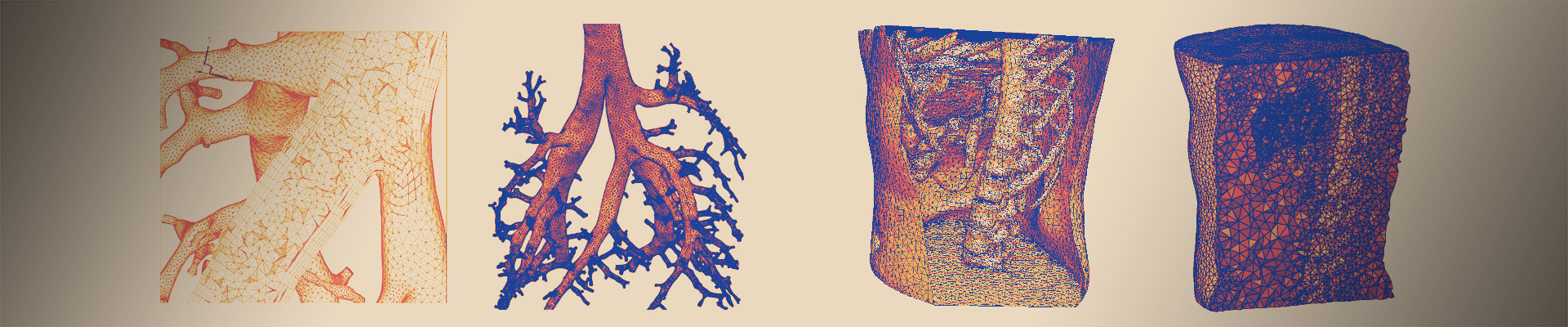
We present a computational multiscale model for the efficient simulation of vascularized tissues, composed of an elastic three-dimensional matrix and a vascular network. The effect of blood vessel pressure on the elastic tissue is surrogated via hyper-singular forcing terms in the elasticity equations, which depend on the fluid pressure. In turn, the blood flow in vessels is treated as a one-dimensional network. The pressure and velocity of the blood in the vessels are simulated using a high-order finite volume scheme, while the elasticity equations for the tissue are solved using a finite element method. This work addresses the feasibility and the potential of the proposed coupled multiscale model. In particular, we assess whether the multiscale model is able to reproduce the tissue response at the effective scale (of the order of millimeters) while modeling the vasculature at the microscale. We validate the multiscale method against a full scale (three-dimensional) model, where the fluid/tissue interface is fully discretized and treated as a Neumann boundary for the elasticity equation. Next, we present simulation results obtained with the proposed approach in a realistic scenario, demonstrating that the method can robustly and efficiently handle the one-way coupling between complex fluid microstructures and the elastic matrix.
Appeared in
- Ann. Biomed. Eng., published online on 20.07.2021, DOI 10.1007/s10439-021-02804-0 .
Download Documents