Modeling, Analysis, and Scaling Limits for Bulk-Interface Processes

Modern devices and materials are heterogeneous and posses a bulk-interface structure. They are composed of different materials joined by thin interfacial layers—lower-dimensional substructures that substantially influence a system’s overall functionality. For example, biological tissue is made of cells including fluidic phases and protein clusters, separated by semipermeable membranes. Metals and rocks consist of crystal grains with different orientation, forming grain boundaries between them. Electronic devices are made of layers of different semiconductor materials, forming interfaces where different materials meet. In all these examples, the interfaces strongly impact the functionality of the whole system: They influence and regulate heat and mass transport, chemical reactions, the response to mechanical forces, optical properties, and electric currents between neighboring bulk phases. Thus, interface processes and bulk processes are always coupled.

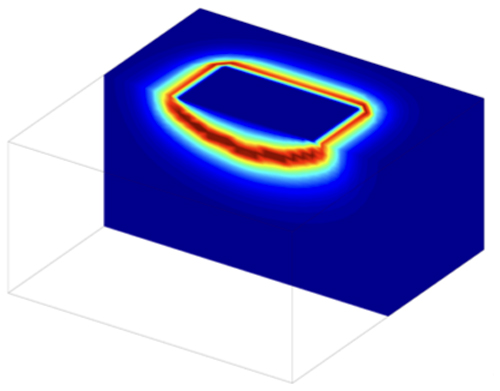
The shape of a sliding liquid droplet is determined by surface energies and by its interaction with an underlying substrate by interfacial friction; cf. Figure 5. The growth of cracks in solid materials can be seen as the creation of new material surfaces with complicated geometry that leads to a release of strain energy; cf. Figure 1. The optical emission of a laser can be substantially enhanced by suitably including thin insulating layers to guide electronic charges into the optically active region; cf. Figure 2. These are only three of the examples of systems with bulk-interface interaction that have been studied mathematically by the Weierstrass Group “Modeling, Analysis, and Scaling Limits for Bulk-Interface Processes” (WG BIP) within several third-party-funded projects, in particular within the DFG Priority Programs SPP 2171 Dynamic Wetting of Flexible, Adaptive, and Switchable Substrates, SPP 1748 Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretisation Methods, Mechanical and Mathematical Analysis, SPP 2256 Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials, the DFG Research Center MATHEON, ECMath – Einstein Center for Mathematics Berlin, and the Berlin Mathematics Research Center MATH+.

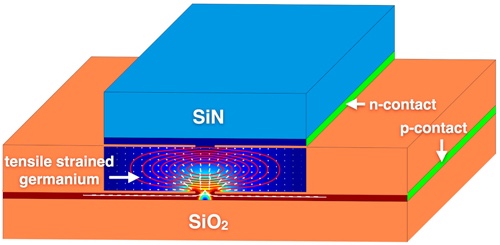
The Weierstrass Group WG BIP was funded for the period 04/2017–06/2023, and it was devoted to the development of mathematical methods for systems with bulk-interface interaction in different applications. For this, an overarching goal of WG BIP was the formulation of a general mathematical structure that supports the mathematical modeling and analysis of processes with bulk-interface coupling in a variational framework. This article highlights some research results that have been achieved by the group in that direction. It is based on joint works of Dirk Peschka (04/2017–09/2023, now RG 1 Partial Differential Equations) and Marita Thomas (04/2017–06/2023, now Freie Universität (FU) Berlin and RG 1) with the former group members Mohammad Hassan Farshbaf Shaker (01/2020–04/2022, now Hochschule für Technik und Wirtschaft Berlin), Xin Liu (01/2021–12/2021, now Texas A&M University), Sven Tornquist (07/2018–09/2022, now FU Berlin), Andrea Zafferi (07/2018–12/2022, now FU Berlin), and many collaborators.

Variational modeling of bulk-interface systems using GENERIC

The variational modeling framework of GENERIC, the acronym for General Equation of Non-Equilibrium Reversible Irreversible Coupling, was originally introduced by Miroslav Grmela and Hans Christian Öttinger in 1997 for thermodynamically closed systems with applications in fluid dynamics. In recent years, its versatility has been proved by different authors also for many other applications such as dissipative solids, complex and reactive fluids, semiconductors and electro-chemistry, quantum mechanics, and thermodynamical multiscale processes. In addition to its physical relevance for thermodynamically consistent modeling, GENERIC is beneficial for mathematicians due to its formulation using abstract operators, function spaces, and functionals. This establishes a sound foundation for mathematical analysis, facilitates the application of multiscale methods, and provides an effective framework to develop structure-preserving numerical solution strategies, particularly in the context of systems of nonlinearly coupled partial differential equations. A GENERIC system is characterized by a quintuple ${\displaystyle (\mathcal{Q},\mathcal{E},\mathcal{S},\mathbb{J},\mathbb{K})}$ consisting of a state space ${\displaystyle \mathcal{Q},}$ the two driving potentials: ${\displaystyle \mathcal{E}}$ the total energy and ${\displaystyle \mathcal{S}}$ the entropy, and two geometric structures: ${\displaystyle \mathbb{J}}$ a Poisson operator and ${\displaystyle \mathbb{K}}$ an Onsager operator. Simple structural properties and variants of GENERIC are illustrated schematically below.

Herein, the triple ${\displaystyle (\mathcal{Q},\mathcal{E},\mathbb{J})}$ forms a Hamiltonian system characterizing the reversible contributions to the dynamics, and the triple ${\displaystyle (\mathcal{Q},\mathcal{S},\mathbb{K})}$ forms a gradient system accounting for the irreversible, dissipative contributions. Both triples are coupled in a GENERIC system, constrained by the additional non-interaction conditions NIC. In thermodynamically closed systems, the NIC automatically ensures conservation of energy and positivity of the entropy production, i.e., the corresponding systems of equations are thermodynamically consistent by construction. The GENERIC evolution equation clearly displays the coupling of reversible and dissipative contributions. The thermodynamical driving forces are the functional derivatives ${\displaystyle \mathrm{D}\mathcal{E}(q)}$ for reversible dynamics and ${\displaystyle \mathrm{D}\mathcal{S}(q)}$ for dissipative dynamics. GENERIC for thermodynamically closed systems generalizes related concepts for energy-driven evolution, e.g., gradient flows for overdamped systems, Hamiltonian dynamics (symplectic flows) for reversible systems, or damped Hamiltonian dynamics for isothermal systems with temperature ${\displaystyle {\theta }^{\ast }}$ . For bulk-interface GENERIC forces ${\displaystyle \mathrm{D}\mathcal{E},\mathrm{D}\mathcal{S}}$ , and states ${\displaystyle q}$ need to be divided into bulk and surface terms.

Bulk-interface GENERIC

One general aim of the WG BIP was to extend the GENERIC framework to systems with bulk-interface interaction. These are systems composed of two (or more) subsystems ${\displaystyle {\mathrm{\Omega }}_{\pm }\subset {\mathbb{R}}^d,}$ coupled with each other along a joint interface ${\displaystyle \mathrm{\Gamma }={{\displaystyle \overline{\mathrm{\Omega }}}}_{+}\cap {{\displaystyle \overline{\mathrm{\Omega }}}}_{-}}$ through which they exchange quantities like heat, stresses, mass, etc. Along ${\displaystyle \mathrm{\Gamma }}$ , also additional processes may take place that are modeled by additional state variables solely defined on ${\displaystyle \mathrm{\Gamma }}$ with individual evolution laws on ${\displaystyle \mathrm{\Gamma },}$ but also driven by the interaction with the quantities from the bulk subdomains ${\displaystyle {\mathrm{\Omega }}_{\pm }}$ . While the compound ${\displaystyle \mathrm{\Omega }=\mathrm{i}\mathrm{n}\mathrm{t}({{\displaystyle \overline{\mathrm{\Omega }}}}_{+}\cup {{\displaystyle \overline{\mathrm{\Omega }}}}_{-})}$ can be assumed to form a thermodynamically closed system, none of the two individual subsystems ${\displaystyle {\mathrm{\Omega }}_{\pm }}$ nor the interface ${\displaystyle \mathrm{\Gamma }}$ do so. Each of these components alone is an open system. A first approach to the GENERIC framework for thermodynamically open systems was proposed by Öttinger in 2006 using driving functionals and geometric structures for the bulk and the boundary components. Following this idea and, based on the definition of functional derivatives for integral functionals with bulk and interfacial contributions, it was proposed in [1] to regard the GENERIC formulation for bulk-interface processes in terms of a weak formulation:

$${\displaystyle \langle q^{\ast },{\mathrm{\partial }}_{t}q{\rangle }_{\mathcal{Q}}=\langle q_{\mathrm{B}}^{\ast },{\mathbb{J}}_{\mathrm{B}}{\mathrm{D}\mathcal{E}}_{\mathrm{B}}(q)+{\mathbb{K}}_{\mathrm{B}}{\mathrm{D}\mathcal{S}}_{\mathrm{B}}(q){\rangle }_{\mathrm{B}}+\langle q_{\mathrm{\Gamma }\gamma }^{\ast },{\mathbb{J}}_{\mathrm{\Gamma }}{\mathrm{D}\mathcal{E}}_{\mathrm{\Gamma }}(q)+{\mathbb{K}}_{\mathrm{\Gamma }}{\mathrm{D}\mathcal{S}}_{\mathrm{\Gamma }}(q){\rangle }_{\mathrm{\Gamma }}(1)}$$

for all suitable test functions ${\displaystyle q^{\ast }=(q_{\mathrm{B}}^{\ast },q_{\mathrm{\Gamma }\gamma }^{\ast })}$ . Above, ${\displaystyle \langle \cdot ,\cdot {\rangle }_{\mathrm{B}},}$ ${\displaystyle \langle \cdot ,\cdot {\rangle }_{\mathrm{\Gamma }}}$ denote suitable dual pairings related to the function spaces on the bulk domain ${\displaystyle \mathrm{\Omega }\mathrm{\backslash }\mathrm{\Gamma }={\mathrm{\Omega }}_{+}\cup {\mathrm{\Omega }}_{-}}$ and on the interface, where both trace spaces induced from the bulk and function spaces for the surface variables are involved. The state vector ${\displaystyle q=(q_{\mathrm{B}},q_{\mathrm{\Gamma }})}$ now consists of variables ${\displaystyle q_{\mathrm{B}}}$ defined on ${\displaystyle \mathrm{\Omega }\mathrm{\backslash }\mathrm{\Gamma }}$ and of surface variables ${\displaystyle q_{\mathrm{\Gamma }}}$ defined on ${\displaystyle \mathrm{\Gamma }}$ . Similarly, also the integral functionals representing energy, entropy, or (dual) dissipation of the bulk-interface system have bulk and surface contributions. More precisely, for ${\displaystyle \mathrm{\Phi }={\mathrm{\Phi }}_{\mathrm{B}}+{\mathrm{\Phi }}_{\mathrm{\Gamma }}}$ as a placeholder for one of these integral functionals, we find that ${\displaystyle \mathrm{\Phi }}$ is of the following form

$${\displaystyle \mathrm{\Phi }(q)={\mathrm{\Phi }}_{\mathrm{B}}(q)+{\mathrm{\Phi }}_{\mathrm{\Gamma }}(q):={\int }_{\mathrm{\Omega }\mathrm{\backslash }\mathrm{\Gamma }}{\varphi }_{\mathrm{B}}(q_{\mathrm{B}},\mathrm{\nabla }{q}_{\mathrm{B}})\mathrm{d}x+{\int }_{\mathrm{\Gamma }}{\varphi }_{\mathrm{\Gamma }}(q_{\mathrm{\Gamma }\gamma })\mathrm{d}s\text{with }{q}_{\mathrm{\Gamma }\gamma }:=({\gamma }_{+}{q}_{+},{\gamma }_{-}{q}_{-},q_{\mathrm{\Gamma }}),}$$

where ${\displaystyle q_{\pm }}$ denotes the restriction of ${\displaystyle q_{\mathrm{B}}}$ to ${\displaystyle {\mathrm{\Omega }}_{\pm }}$ and ${\displaystyle {\gamma }_{\pm }{q}_{\pm }}$ its trace on ${\displaystyle {\mathrm{\Gamma }}_{\pm }=\mathrm{\partial }{\mathrm{\Omega }}_{\pm }\cap \mathrm{\Gamma }}$ the part of the boundary of ${\displaystyle {\mathrm{\Omega }}_{\pm }}$ that belongs to ${\displaystyle \mathrm{\Gamma }}$ . Accordingly, the functional derivative reads

$$\begin{array}{c}\text{D}\Phi (q)[\tilde{q}]={\displaystyle {\int }_{\mathrm{\Omega }\mathrm{\backslash }\mathrm{\Gamma }}({\partial }_{q_{\text{B}}}{\varphi }_{\text{B}}(q_{\text{B}},\nabla q_{\text{B}})-\text{div\hspace{0.05em}}{\partial }_{\nabla q_{\text{B}}}{\varphi }_{\text{B}}(q_{\text{B}},\nabla q_{\text{B}})){\tilde{q}}_{\text{B}}\text{d}x}\\ +{\displaystyle \sum _{i\in \{+,-\}}{\int }_{\mathrm{\Gamma }}({\partial }_{\nabla q_i}{\varphi }_{\text{B}}({\gamma }_i{q}_i,{\gamma }_i\nabla q_i){\text{n}}_i+{\partial }_{q_i}{\varphi }_{\mathrm{\Gamma }}({\gamma }_{+}{q}_{+},{\gamma }_{-}{q}_{-},q_{\mathrm{\Gamma }})){\gamma }_i{\tilde{q}}_i\text{d}s}\\ +{\displaystyle {\int }_{\mathrm{\Gamma }}{\partial }_{q_{\mathrm{\Gamma }}}{\varphi }_{\mathrm{\Gamma }}({\gamma }_{+}{q}_{+},{\gamma }_{-}{q}_{-},q_{\mathrm{\Gamma }}){\tilde{q}}_{\mathrm{\Gamma }}\text{d}s}\end{array}(2)$$

for all suitable test functions ${\displaystyle \tilde{q}}$ . Regarding ${\displaystyle \mathrm{D}\mathrm{\Phi }(q)}$ as a force acting on ${\displaystyle {\displaystyle \tilde{q}},}$ (2) states its split into bulk and interface forces. Similarly, also the Poisson and Onsager operators ${\displaystyle \mathbb{J}}$ and ${\displaystyle \mathbb{K}}$ are composed by a bulk and a surface contribution, which can only act on the corresponding bulk and surface terms of the driving forces ${\displaystyle \mathrm{D}\mathcal{E}(q)}$ and ${\displaystyle \mathrm{D}\mathcal{S}(q)}$ . In view of (2), interfacial coupling conditions are thus displayed in the weak form of GENERIC (1) as a natural outcome.

Heat conduction as an example for bulk-interface GENERIC

As an example, we discuss here the Onsager structure for heat conduction taking into account different interfacial Onsager operators along ${\displaystyle \mathrm{\Gamma }}$ and thus resulting in different coupling conditions. The state vector ${\displaystyle q_{\mathrm{\Gamma }\gamma }=({\gamma }_{+}{q}_{+},{\gamma }_{-}{q}_{-}{)}^{\mathrm{\top }}}$ here only accounts for the traces of the bulk variables, since there are no additional interfacial variables ${\displaystyle q_{\mathrm{\Gamma }}}$ with an evolution law described on the interface.

Heat conduction in the bulk ${\displaystyle {\mathrm{\Omega }}_{+}\cup {\mathrm{\Omega }}_{-}}$ : The dual dissipation potential in the bulk is defined as

$${\displaystyle {\mathrm{\Psi }}_{\mathrm{B}}^{\ast }(\theta ;\cdot ):Q^{\ast }\to \mathbb{R},{\mathrm{\Psi }}_{\mathrm{B}}^{\ast }(\theta ;\xi ):={\displaystyle \sum _{i\in \{+,-\}}}{\int }_{{\mathrm{\Omega }}_i}\frac{{\theta }^2\kappa (\theta )}{2}{\left|\mathrm{\nabla }\left(\frac{\xi }{{\mathrm{D}}_{\theta }E}\right)\right|}^2\mathrm{d}x,}$$

where ${\displaystyle {\mathcal{Q}}^{\ast }}$ denotes the dual space of a suitable Banach space ${\displaystyle \mathcal{Q}}$ and where the temperature ${\displaystyle \theta }$ is related to the energy and entropy densities ${\displaystyle E,S}$ through the Gibbs relation $\theta =\frac{{\mathrm{D}}_{\theta }E}{{\mathrm{D}}_{\theta }S}$ . Its functional derivative generates the bulk Onsager operator ${\displaystyle {\mathbb{K}}_{\mathrm{B}}}$ , and it reads

$$\begin{array}{l}{\displaystyle {\displaystyle {\mathrm{D}}_{\xi }{\mathrm{\Psi }}_{\mathrm{B}}^{\ast }(\theta ;\xi )[{\displaystyle \tilde{\xi }}]=}}{\displaystyle {\displaystyle {\displaystyle \sum _{i\in \{+,-\}}}{\int }_{{\mathrm{\Omega }}_i}-\mathrm{div}\left({\theta }^2\kappa (\theta )\mathrm{\nabla }(\frac{\xi }{{\mathrm{D}}_{\theta }E})\right)\frac{{\displaystyle \tilde{\xi }}}{{\mathrm{D}}_{\theta }E}\mathrm{d}x+{\int }_{{\mathrm{\Gamma }}_i}{\gamma }_i\left({\theta }_i^2\kappa ({\theta }_i)\mathrm{\nabla }(\frac{{\xi }_i}{{\mathrm{D}}_{\theta }{E}_i})\right)\cdot {\mathrm{n}}_i{\gamma }_i\left(\frac{{{\displaystyle \tilde{\xi }}}_i}{{\mathrm{D}}_{\theta }{E}_i}\right)\mathrm{d}s}}\\ {\displaystyle =:}{\displaystyle \langle {\mathbb{K}}_{\mathrm{B}}(\theta )\xi ,{\displaystyle \tilde{\xi }}{\rangle }_Q.}\end{array}$$

Here, ${\displaystyle {\gamma }_i{a}_i}$ denotes the trace of the function ${\displaystyle a_i=a|{}_{{\mathrm{\Omega }}_i}}$ on the interface ${\displaystyle {\mathrm{\Gamma }}_i=\mathrm{\Gamma }\cap {{\displaystyle \overline{\mathrm{\Omega }}}}_i}$ for ${\displaystyle i\in \{+,-\}}$ .

Ideal heat transfer across the perfectly conducting interface ${\displaystyle \mathrm{\Gamma }}$ : At the perfectly conducting interface ${\displaystyle \mathrm{\Gamma }}$ , all quantities are continuous, which implies ${\displaystyle {\gamma }_{+}{{\displaystyle \tilde{\xi }}}_{+}={\gamma }_{-}{{\displaystyle \tilde{\xi }}}_{-}}$ for the test functions, and

$${\displaystyle {\displaystyle {\gamma }_{+}\left(\frac{{\theta }_{+}^2{\kappa }_{+}({\theta }_{+})}{{\mathrm{D}}_{\theta }{E}_{+}}\mathrm{\nabla }\left(\frac{{\xi }_{+}}{{\mathrm{D}}_{\theta }{E}_{+}}\right)\right)\cdot {\mathrm{n}}_{+}=-{\gamma }_{-}\left(\frac{{\theta }_{-}^2{\kappa }_{-}({\theta }_{-})}{{\mathrm{D}}_{\theta }{E}_{-}}\mathrm{\nabla }\left(\frac{{\xi }_{-}}{{\mathrm{D}}_{\theta }{E}_{-}}\right)\right)\cdot {\mathrm{n}}_{-}.}}$$

he first condition then is encoded in a suitable choice of the function space ${\displaystyle {\mathcal{Q}}^{\ast }}$ . Integration by parts in ${\displaystyle \langle {\mathbb{K}}_{\mathrm{B}}(\theta )\xi ,{\displaystyle \tilde{\xi }}{\rangle }_{\mathcal{Q}}}$ shows that the Onsager operator ${\displaystyle {\mathbb{K}}_{\mathrm{B}}}$ is symmetric and positively definite. Applying it to ${\displaystyle \xi =\mathrm{D}E}$ shows that also the non-interaction conditions are satisfied.

Heat transfer across the imperfect interface ${\displaystyle \mathrm{\Gamma }}$ : We assume that the heat transfer through ${\displaystyle \mathrm{\Gamma }}$ is regulated by the heat transfer coefficient ${\displaystyle {{\displaystyle \widehat{\kappa }}}_{\mathrm{\Gamma }}({\gamma }_{+}{\theta }_{+},{\gamma }_{-}{\theta }_{-})}$ . In this spirit, we introduce the quadratic dual dissipation potential along ${\displaystyle \mathrm{\Gamma },}$ for every suitable ${\displaystyle {\xi }_{\gamma }=({\xi }_{+},{\xi }_{-}{)}^{\mathrm{\top }}}$

$${\displaystyle {\mathrm{\Psi }}_{\mathrm{\Gamma }}^{\ast }({\theta }_{\gamma };{\xi }_{\gamma }):={\int }_{\mathrm{\Gamma }}\frac{{{\displaystyle \widehat{\kappa }}}_{\mathrm{\Gamma }}({\gamma }_{+}{\theta }_{+},{\gamma }_{-}{\theta }_{-})}{2}|{\gamma }_{+}\left(\frac{{\xi }_{+}}{{\mathrm{D}}_{\theta }{E}_{+}}\right)-{\gamma }_{-}\left(\frac{{\xi }_{-}}{{\mathrm{D}}_{\theta }{E}_{-}}\right){|}^2\mathrm{d}s,}$$

and we find for all suitable ${\displaystyle {\xi }_{\gamma },{{\displaystyle \tilde{\xi }}}_{\gamma }}$ that

$$\begin{array}{ll}{\mathrm{D}}_{{\xi }_{\gamma }}{\mathrm{\Psi }}_{\mathrm{\Gamma <!--\; G\; -->}}^{\ast <!--\; *\; -->}({\theta }_{\gamma };{\xi }_{\gamma })[{\stackrel{~<!--\; ~\; -->}{\xi }}_{\gamma }]& ={\int }_{\mathrm{\Gamma <!--\; G\; -->}}{\stackrel{^<!--\; ^\; -->}{\kappa }}_{\mathrm{\Gamma <!--\; G\; -->}}({\theta }_{\gamma })({\gamma }_{+}(\frac{{\xi }_{+}}{{\mathrm{D}}_{\theta }{E}_{+}})-<!--\; -\; -->{\gamma }_{-<!--\; -\; -->}(\frac{{\xi }_{-<!--\; -\; -->}}{{\mathrm{D}}_{\theta }{E}_{-<!--\; -\; -->}}))({\gamma }_{+}(\frac{{\stackrel{~<!--\; ~\; -->}{\xi }}_{+}}{{\mathrm{D}}_{\theta }{E}_{+}})-<!--\; -\; -->{\gamma }_{-<!--\; -\; -->}(\frac{{\stackrel{~<!--\; ~\; -->}{\xi }}_{-<!--\; -\; -->}}{{\mathrm{D}}_{\theta }{E}_{-<!--\; -\; -->}}))\mathrm{d}s\\ & =:⟨{\mathbb{K}}_{\mathrm{\Gamma <!--\; G\; -->}}({\theta }_{\gamma }){\xi }_{\gamma },{\stackrel{~<!--\; ~\; -->}{\xi }}_{\gamma }{⟩}_{{\stackrel{~<!--\; ~\; -->}{\mathcal{Q}}}_{\mathrm{\Gamma <!--\; G\; -->}}}.\end{array}$$

Clearly, ${\displaystyle {\mathbb{K}}_{\mathrm{\Gamma }}({\theta }_{\gamma })}$ is symmetric and positively semidefinite provided that ${\displaystyle {{\displaystyle \widehat{\kappa }}}_{\mathrm{\Gamma }}({\theta }_{\mathrm{\Gamma }})\ge 0}$ . Choosing ${\displaystyle {\xi }_{\gamma }=({\mathrm{D}}_{\theta }{E}_{+},{\mathrm{D}}_{\theta }{E}_{-}{)}^{\mathrm{\top }}}$ above shows that also the non-interaction condition holds true. Thus, also the Onsager operator of the full system ${\displaystyle \mathbb{K}(\theta )={\mathbb{K}}_{\mathrm{B}}(\theta )+{\mathbb{K}}_{\mathrm{\Gamma }}({\theta }_{\gamma })}$ is symmetric, positively semidefinite, and satisfies the non-interaction conditions.

Now, the evolution equation of the system can be understood in a weak form (1), such that for a.a. ${\displaystyle t\in (0,T)}$ and for all ${\displaystyle {\displaystyle \tilde{\xi }}\in {\displaystyle \tilde{\mathcal{Q}}}=H^1(\mathrm{\Omega }\mathrm{\backslash }\mathrm{\Gamma })}$ there holds

$${\displaystyle {\displaystyle \langle {\displaystyle \dot{\theta }},{\displaystyle \tilde{\xi }}{\rangle }_{{\displaystyle \tilde{\mathcal{Q}}}}}}{\displaystyle {\displaystyle =\langle \mathbb{K}(\theta ){\mathrm{D}}_{\theta }\mathcal{S}(\theta ),{\displaystyle \tilde{\xi }}{\rangle }_{{\displaystyle \tilde{\mathcal{Q}}}}=\langle {\mathbb{K}}_{\mathrm{B}}(\theta ){\mathrm{D}}_{\theta }\mathcal{S}(\theta ),{\displaystyle \tilde{\xi }}{\rangle }_{H^1(\mathrm{\Omega }\mathrm{\backslash }\mathrm{\Gamma })}+\langle {\mathbb{K}}_{\mathrm{\Gamma }}({\theta }_{\mathrm{\Gamma }}){\mathrm{D}}_{\theta }{\mathcal{S}}_{\mathrm{\Gamma }}(\theta ),{{\displaystyle \tilde{\xi }}}_{\mathrm{\Gamma }}{\rangle }_{H^{1/2}(\mathrm{\Gamma })}.}}$$

For a closed system, the heat flux through the boundary vanishes, i.e., ${\displaystyle {\theta }^2\kappa (\theta )\mathrm{\nabla }(\frac{{\mathrm{D}}_{\theta }S}{{\mathrm{D}}_{\theta }E})\frac{1}{{\mathrm{D}}_{\theta }E}\cdot {\mathrm{n}}_{\mathrm{\partial }\mathrm{\Omega }}=0}$ on ${\displaystyle \mathrm{\partial }\mathrm{\Omega }.}$ Hence, choosing test functions ${\displaystyle {\displaystyle \tilde{\xi }}={\mathrm{D}}_{\theta }E{\displaystyle \widehat{\xi }}}$ with ${\displaystyle {\displaystyle \widehat{\xi }}\in {\displaystyle \tilde{\mathcal{Q}}}}$ and using the Gibbs relation, there holds in a weak sense

$${\displaystyle {\mathrm{D}}_{\theta }E{\displaystyle \dot{\theta }}=-\mathrm{div}({\theta }^2\kappa (\theta )\mathrm{\nabla }\frac{1}{\theta })\text{ in }\mathrm{\Omega }\mathrm{\backslash }\mathrm{\Gamma }}$$

for a.a. ${\displaystyle t\in (0,T),}$ together with the following transmission conditions along ${\displaystyle \mathrm{\Gamma }}$

$$\begin{array}{lll}{\gamma }_{+}(\frac{{\theta }_{+}^2{\kappa }_{+}({\theta }_{+})}{{\text{D}}_{\theta }{E}_{+}}\nabla (\frac{1}{{\theta }_{+}}))\cdot {\text{n}}_{+}\hfill & =\hfill & -{\gamma }_{-}(\frac{{\theta }_{-}^2{\kappa }_{-}({\theta }_{-})}{{\text{D}}_{\theta }{E}_{-}}\nabla (\frac{1}{{\theta }_{-}}))\cdot {\text{n}}_{-},\hfill \\ {\gamma }_{+}(\frac{{\theta }_{+}^2{\kappa }_{+}({\theta }_{+})}{{\text{D}}_{\theta }{E}_{+}}\nabla (\frac{1}{{\theta }_{+}}))\cdot {\text{n}}_{+}\hfill & =\hfill & -{{\displaystyle \widehat{\kappa }}}_{\mathrm{\Gamma }}({\theta }_{\gamma })(\frac{1}{{\gamma }_{+}{\theta }_{+}}-\frac{1}{{\gamma }_{-}{\theta }_{-}})=\frac{{{\displaystyle \widehat{\kappa }}}_{\mathrm{\Gamma }}({\theta }_{\gamma })}{{\gamma }_{+}{\theta }_{+}{\gamma }_{-}{\theta }_{-}}({\gamma }_{+}{\theta }_{+}-{\gamma }_{-}{\theta }_{-}),\hfill \end{array}$$

complemented by the above homogeneous boundary condition along ${\displaystyle \mathrm{\partial }\mathrm{\Omega }}$ and by an initial condition.

Heat conduction provides a simple example to illustrate how different phenomena of bulk-interface interaction can be described with the aid of the weak form of GENERIC and how interfacial coupling conditions arise as a natural outcome of this formulation. This framework also applies to more complex systems with bulk-interface coupling, as we further address below.

Fluid-structure interaction

Fluid-structure interaction (FSI) is another example of a larger class of bulk-interface systems that do not need additional state variables to be defined on interfaces, but rather require the systematic decomposition of driving forces from different types of physics in different subdomains of the system into contributions from the bulk and from the interface. Then, the operators acting on these contributions need to be defined consistently with the GENERIC formalism shown schematically above. In [2], the GENERIC formalism is applied to deduce a weak form of a damped Hamiltonian system describing FSI using a representation ${\displaystyle \xi =({\xi }_{\mathrm{B}},{\xi }_{\mathrm{\Gamma }})}$ of bulk forces ${\displaystyle {\xi }_{\mathrm{B}}}$ and interface forces ${\displaystyle {\xi }_{\mathrm{\Gamma }}}$ via a decomposition

$${\displaystyle \langle \mathrm{D}\mathcal{E}(q),v\rangle ={\int }_{\mathrm{\Omega }}{\xi }_{\mathrm{B}}\cdot v\mathrm{d}x+{\int }_{\mathrm{\Gamma }}{\xi }_{\mathrm{\Gamma }}\cdot v|{}_{\mathrm{\Gamma }}\mathrm{d}s=b(\xi ,v),}(3)$$

where the energy $\mathcal{E}(q)={\int }_{\mathrm{\Omega }\backslash \mathrm{\Gamma }}E(q,\mathrm{\nabla }q)\mathrm{d}x$ has a density ${\displaystyle E}$ that has only a bulk part and only depends on the bulk state and its gradient without distinguished contributions on the interface. However, the dependence on ${\displaystyle \mathrm{\nabla }q}$ generates mechanical contributions in the Piola–Kirchhoff stress in the bulk and on the interface that need to be properly transmitted through a solid-fluid interface. This was achieved in [2] with the ansatz described in the previous paragraphs and by making use of a general formalism for Lagrangian-Eulerian coordinate transformations within GENERIC that was established in [3]. In particular, it was shown in this work that such transformations preserve the structural properties of a GENERIC system. Typical Lagrangian contributions to ${\displaystyle E}$ include kinetic energy ${\displaystyle \frac{p^2}{2\varrho }}$ , hyperelastic energy ${\displaystyle E_{\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{s}\mathrm{t}}(F)}$ with deformation gradient ${\displaystyle F=\mathrm{\nabla }\chi }$ , or an internal energy ${\displaystyle E_{\mathrm{i}\mathrm{n}\mathrm{t}}(\frac{\varrho }{detF})}$ for a compressible fluid. One key observation in [2] is that the weak form (1) of the FSI system can be rewritten as a nonlinear saddle-point problem for ${\displaystyle q(t),\xi (t)}$

$${\displaystyle {\displaystyle a(\xi (t),\eta )-b(\eta ,{\mathrm{\partial }}_{t}q(t))}}{\displaystyle {\displaystyle =}}{\displaystyle {\displaystyle 0,}}\text{(4a)}$$ $${\displaystyle {\displaystyle b(\xi (t),v)}}{\displaystyle {\displaystyle =}}{\displaystyle {\displaystyle \langle \mathrm{D}\mathcal{E}(q(t)),v\rangle }}\text{(4b)}$$

to be satisfied for all suitable test functions ${\displaystyle v,\eta }$ . Here, for this damped Hamiltonian system, the bilinear form ${\displaystyle a=j-k}$ is the difference of a skew-symmetric part ${\displaystyle j}$ and a positive definite, symmetric part ${\displaystyle k}$ , induced by the Poisson operator ${\displaystyle {\mathbb{J}}_{\mathrm{B}}}$ and the Onsager operator ${\displaystyle {\mathbb{K}}_{\mathrm{B}}}$ comprising the bulk contributions of the fluid and the solid in the weak form (1).

The saddle-point formulation (4) is a useful approach for numerical implementation. Figure 4 shows a snapshot of a corresponding nonlinear elastodynamics modeled by (4). These and similar mathematical modeling approaches were investigated within the Thematic Einstein Semester Energy-based mathematical methods for reactive multiphase flows, co-organized by members of WG BIP in 2020/21.

Moving contact lines

Free boundary problems with moving contact lines are one important class of problems that require a force decomposition (3) and that were investigated in WG BIP. One main feature of this particular type of problem is that domains evolve over time ${\displaystyle \mathrm{\Omega }=\mathrm{\Omega }(t)}$ . Therefore, derivatives ${\displaystyle \mathrm{D}\mathcal{E}(q)}$ need to incorporate appropriate shape derivatives of the time-dependent domains. Surface energies of the form ${\mathcal{E}}_{\mathrm{\Gamma }}={\int }_{\mathrm{\Gamma }}\mathrm{d}s$ then produce forces proportional to mean curvature on interfaces ${\displaystyle \mathrm{\Gamma }(t)}$ and conditions for contact angles on ${\displaystyle \mathrm{\partial }\mathrm{\Gamma }(t)}$ . The strategy is to reformulate these problems in the form of (4) to provide a GENERIC framework that can be discretized in time using time-incremental schemes and in space using finite elements.

Corresponding higher-order space and time discretizations for thin-film type models with dynamic contact angles are developed jointly with Luca Heltai, cf. 10.1016/j.jcp.2022.111325, and self-similar solutions are studied in [4]. The main challenge of these higher-order parabolic equations ${\displaystyle {\mathrm{\partial }}_{t}h-\mathrm{\nabla }\cdot (m(h)\mathrm{\nabla }\xi )=0}$ for the film height ${\displaystyle h}$ is the degeneracy in the mobility ${\displaystyle m(h)\to 0}$ as ${\displaystyle h\to 0}$ . This makes the evolution of the support set ${\displaystyle \mathrm{\Omega }(t)=\{x:h(x,t)>0\}}$ a free boundary problem that requires appropriate bulk-interface coupling techniques on ${\displaystyle \mathrm{\partial }\mathrm{\Omega }(t)}$ . There it turned out, with suitable choices of the bilinear forms ${\displaystyle a,b}$ in (4) and corresponding function spaces for ${\displaystyle q}$ and ${\displaystyle \xi }$ , that the mixed formulation is also suitable to study model hierarchies for vanishing dissipation or mobility and develop efficient discretization schemes for the emerging free boundary problems.

In [5], molecular dynamics (MD) predictions for droplets moving over rough surfaces were compared with continuum hydrodynamic models based on finite element method (FEM) computations; cf. Figure 5. The goal of this interdisciplinary research is to identify scaling regimes, where surface roughness leads to enhanced or reduced energy dissipation and, therefore, can be effectively treated using bulk-interface coupling techniques. For that reason, the gradient system contains dissipation potentials contributing in the bulk (3D), on interfaces (2D), and at contact lines (1D) and was combined with suitable arbitrary Lagrangian-Eulerian (ALE) techniques to efficiently treat the motion of moving meshes.

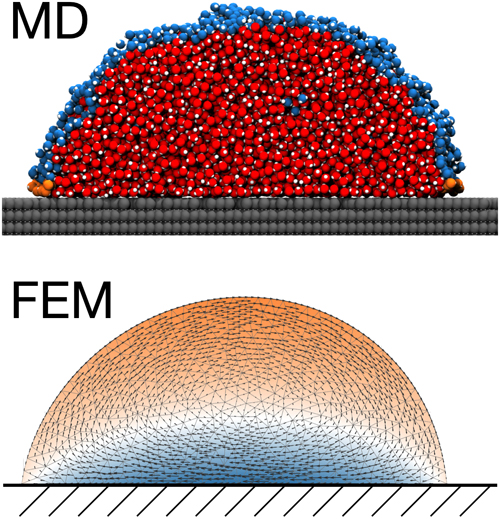
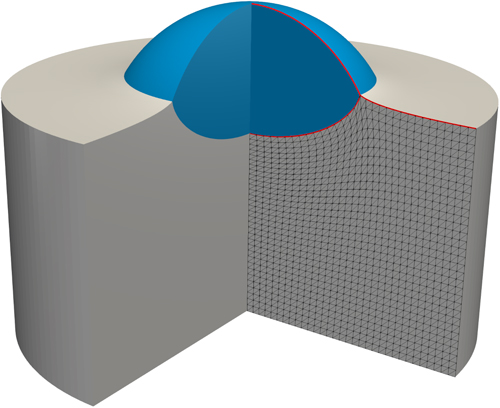
Similar axisymmetric models are also developed to investigate sharp-interface limits of phase field models for FSI with moving contact lines. One of the main observations is that scaling limits ${\displaystyle \epsilon \to 0}$ for coupled Navier–Stokes–Cahn–Hilliard systems depend on the scaling of the Cahn–Hilliard mobility ${\displaystyle m_{\epsilon }=m_0{\epsilon }^{\alpha }}$ and are valid in a certain range ${\displaystyle {\displaystyle \underset{\_}{\alpha }}<\alpha <{\displaystyle \overline{\alpha }}}$ only. Depending on the norm for the sharp-interface limit, this range narrows down for multiphase systems with contact lines; cf. Figure 6.

Propagation of delamination and fracture

Models to describe the propagation of delamination, i.e., crack growth along prescribed interfaces, provide an example for bulk-interface GENERIC where the evolution law of an additional variable ${\displaystyle q_{\mathrm{\Gamma }}}$ is prescribed on the interface. This delamination variable ${\displaystyle q_{\mathrm{\Gamma }}}$ characterizes the state of the material along the interface and evolves from the unbroken state ${\displaystyle q_{\mathrm{\Gamma }}(0,x)=1}$ to the fully broken state ${\displaystyle q_{\mathrm{\Gamma }}(t,x)=0}$ in a material point ${\displaystyle x\in \mathrm{\Gamma }}$ . A typical evolution law for ${\displaystyle q_{\mathrm{\Gamma }}}$ is given in terms of a subdifferential inclusion

$${\displaystyle -{\mathrm{D}}_{q_{\mathrm{\Gamma }}}{\mathcal{E}}_{\mathrm{\Gamma }}(q_{\mathrm{B}},q_{\mathrm{\Gamma }})\in \mathrm{\partial }\mathrm{\Psi }(q;{{\displaystyle \dot{q}}}_{\mathrm{\Gamma }}).}$$

This inclusion stems from the fact that for fracture problems the dissipation potential ${\displaystyle \mathrm{\Psi }(q;\cdot )}$ is typical nonsmooth with ${\displaystyle \mathrm{\Psi }(q;v_{\mathrm{\Gamma }})=\mathrm{\infty }}$ if ${\displaystyle v_{\mathrm{\Gamma }}>0}$ in order to exclude the healing of the material in the model. Typical interfacial energy densities ${\displaystyle E_{\mathrm{\Gamma }}(q_{\mathrm{B}},q_{\mathrm{\Gamma }})}$ depend on ${\displaystyle q_{\mathrm{\Gamma }}}$ and on functions of the jump of the displacement field across ${\displaystyle \mathrm{\Gamma }}$ and thus result by means of (1) in coupling conditions between the normal stresses from the bulk and the interfacial stresses. It was shown in [1] that typical delamination models, as they are used in engineering literature and as they have been investigated analytically, e.g., in [6], can be understood in a weak form of GENERIC (1). In particular, the analysis in a series of works on delamination related to [6] already makes use of this structure and provides structure-preserving approximations for different types of delamination models by means of suitable discretization schemes and variational convergence methods.

Conclusions and outlook

The weak form of GENERIC (1) and the weak saddle-point structure (4) for damped Hamiltonian systems have proven a versatile modeling framework for systems with bulk-interface interaction, which naturally takes into account interfacial coupling conditions between the different subsystems. These structures have been used as a basis for mathematical analysis and numerical implementations for models from different applications with the benefit that the structure can be preserved during approximation. Future investigations will be devoted, amongst others, to geophysical and biological applications such as FSI related to sea ice dynamics and biological hydrogels.

References

1. M. Thomas, M. Heida, GENERIC for dissipative solids with bulk–interface interaction, in: Research in Mathematics of Materials Science, M.I. Español, M. Lewicka, L. Scardia, A. Schlömerkemper, eds., vol. 31 of Association for Women in Mathematics Series, Springer, Cham, 2022, pp. 333–364.
2. D. Peschka, A. Zafferi, L. Heltai, M. Thomas, Variational approach to fluid-structure interaction via GENERIC, J. Non-Equilib. Thermodyn., 47:2 (2022), pp. 217–226.
3. A. Zafferi, D. Peschka, M. Thomas, GENERIC framework for reactive fluid flows, ZAMM Z. Angew. Math. Mech., 103:7 (2022), e202100254/1–e202100254/70.
4. L. Giacomelli, M.V. Gnann, D. Peschka, Droplet motion with contact-line friction: Long-time asymptotics in complete wetting, Proc. R. Soc. Lond. Ser. A, 479:2274 (2023), 20230090/1–20230090/23.
5. A.K. Giri, P. Malgaretti, D. Peschka, M. Sega, Resolving the microscopic hydrodynamics at the moving contact line, Phys. Rev. Fluids, 7 (2022), L102001/1–L102001/9.
6. R. Rossi, M. Thomas, From adhesive to brittle delamination in visco-elastodynamics, Math. Models Methods Appl. Sci., 27:08 (2017), pp. 1489–1546.