MATH+ Project EF3-9
Mathematical Framework for MR Poroelastography
| Project heads | Alfonso Caiazzo (WIAS), Karsten Tabelow (WIAS), Prof. Ingolf Sack (Charité), |

|
|---|---|---|
| Staff | Felipe Galarce | |
| Funding period | January 1st, 2021 - December 31st, 2021 | |
| Funding agency | MATH+ | |
BACKGROUND
Medical imaging of tissues based on MRI enables the non-invasive quantitative characterization of important biomarkers, and it is therefore a pillar of clinical diagnostic of tissue diseases. Biological tissues are by nature poroelastic and the understanding of biphasic aspects such as porosity and interstitial pressure might provide the identification of abnormal pressure increase in the cardiovascular system or cerebro-spinal fluid. To this purpose, the mechanical behavior of the tissue is modeled as a biphasic material. Due to the large number of unknowns, the quantification of poroelastic parameters requires additional knowledge about the tissue microstructure, typically beyond clinically available image resolution.
Magnetic resonance elastography (MRE) is an imaging technique sensitive to the stiffness properties of tissues. In MRE, the propagation of shear waves in the audible frequency range (10 - 1000 Hz) through the tissue - recorded as a three-dimensional image of the inner displacement field - is combined with suitable mathematical and computational tissue models [9, 4] in order to obtain elastograms, i.e., a 3D maps of tissue elastic parameters. The displacement data - with a typical resolution of the order of millimeters - currently allow the reconstruction of tissue models only at the effective scale, i.e., with mechanical parameters varying only at a coarse spatial resolution level. Therefore, in the context of poroelastic tissues, MRE shall be supported by advanced computational and mathematical models in order to bridge the gap between the scale of available data (tissue displacement) and the scale of the microstructural parameters.
Inversion recovery (IR) denotes a spin echo MR sequence with a 180-degree inverting pulse. The following relaxation of the MRI signal is governed by the T1 relaxation time which depends on the tissue properties. This observation motivated recent experiments performed at the Charit á Berlin (MRE Group of Prof. Sack) aimed at obtaining T1 and porosity maps in the tissue via IR, using different times for the inversion pulse and describing the MR signal via a bi-exponential model.
The project builds upon a recently started collaboration between WIAS and the MRE group at Charité. Within the project, this interaction will be also linked to the BIOQIC research training network, a research training network that aims at promoting multidisciplinary research in clinical imaging sciences.
PROJECT GOALS
The goal of this project is to support the development of efficient and high-resolution protocol for imaging poroelastic parameters of tissues via MRI, by combining data acquired with two image modalities - inversion recovery and MR elastography - with advanced statistical image processing and multiscale numerical methods. In particular, the main objectives of the research will be- to increase the robustness of the porosity map estimation via IR,
- to design an optimal acquisition sequence for the inversion recovery experiment,
- to develop efficient numerical methods for addressing the multiscale inverse problems of recovering poroelastic parameters from MRE data, and
- to validate the algorithms in realistic clinical settings.
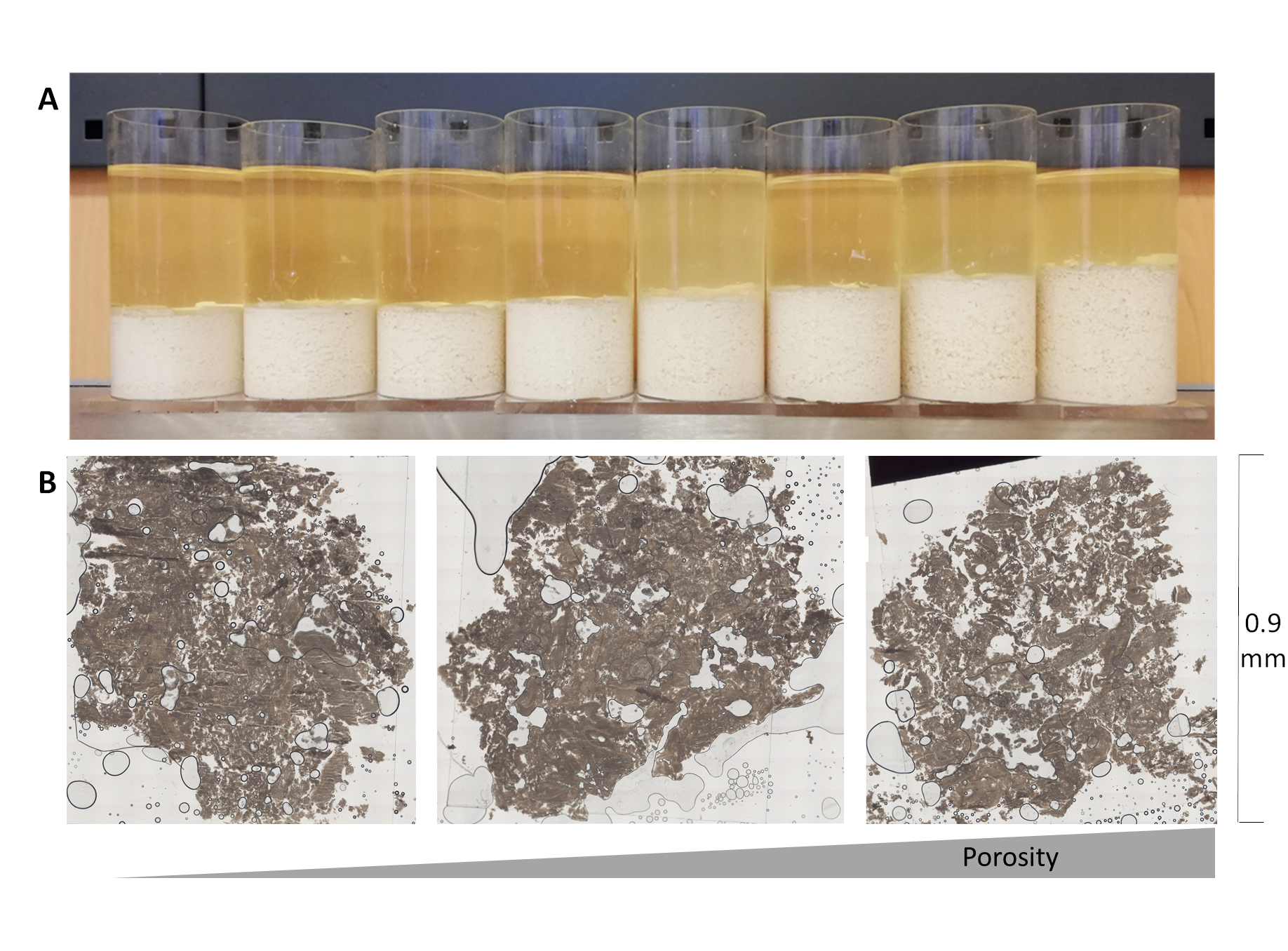
Tofu samples (top) and selected slices for the experimental evaluation (draining) of porosity
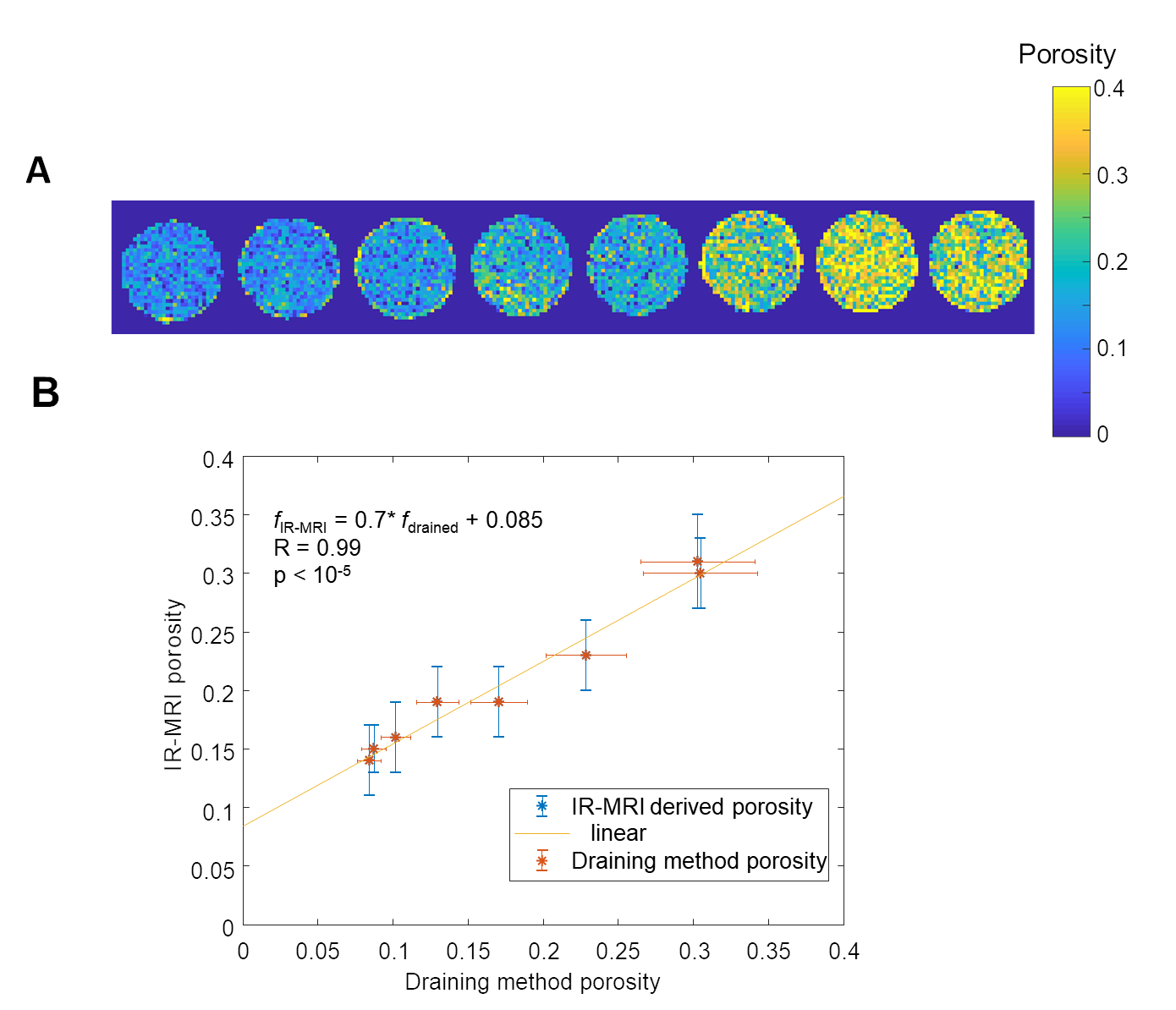
Porosity estimated via IR-MRI (top) and validation against experimental values
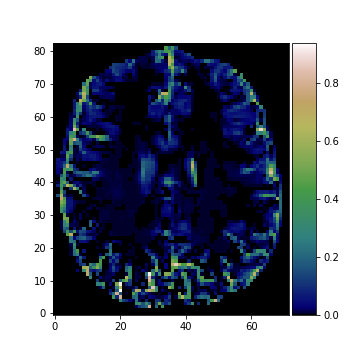
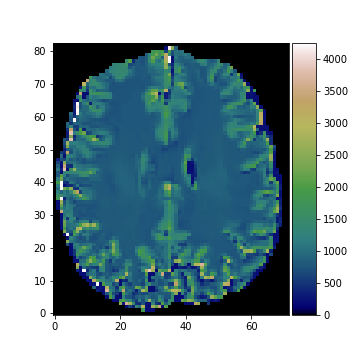
Porosity map and T1-map estimated using IR-MRI and adaptive smoothing
PUBLICATIONS
- (Lilaj et al. 2021) L. Lilaj, T. Fischer, J. Guo, J. Braun, I. Sack, S. Hirsch. Separation of fluid and solid shear wave fields and quantification of coupling density by
magnetic resonance poroelastography. Magn Reson Med. 2021 Mar;85(3):1655-1668. doi: 10.1002/mrm.28507.
REFERENCES
- [1] A. Caiazzo, R. Maier, and D. Peterseim. Reconstruction of quasi-local numerical effective models from low-resolution measurements. J. Sci. Comp. 85, 10 (2020).
- [2] J. Polzehl and K. Tabelow. Magnetic Resonance Brain Imaging: Modeling and Data Analysis Using R. Springer, 2019.
- [3] K. Tabelow, E. Balteau, J. Ashburner, M.F. Callaghan, B. Draganski, G. Helms, F. Kherif, T. Leutritz, A. Lutti, Ch. Phillips, E. Reimer, L. Ruthotto, M. Seif, N. Weiskopf, G. Ziegler, and S. Mohammadi. hMRI - a toolbox for quantitative MRI in neuroscience and clinical research. NeuroImage, 194:191-210, 2019.
- [4] I. Sack and T. Schäffter, editors. Quantification of Biophysical Parameters in Medical Imaging. Springer, 2018.
- [5] L. Blank, A. Caiazzo, F. Chouly, A. Lozinski, and J. Mura. Analysis of a stabilized penalty- free Nitsche method for the Brinkman, Stokes, and Darcy problems. ESAIM: Mathematical Modeling and Numerical Analysis (M2AN), 52(6):2149-2185, 2018.
- [6] L. Tan, M. D. J. McGarry, E. W. Van Houten, M. Ji, L. Solamen, W. Zeng, J.B. Weaver, and K. D. Paulsen. A numerical framework for interstitial fluid pressure imaging in poroelastic MRE. PLOS ONE, 12(6):1-22, 06 2017.
- [7] J. Polzehl and K. Tabelow. Low SNR in diffusion MRI models. J. Amer. Statist. Assoc., 111(516):1480-1490, 2016.
- [8] A. Caiazzo and J. Mura. M Multiscale modeling of weakly compressible elastic materials in the harmonic regime and applications to microscale structure estimation. SIAM Mult. Mod. Sim., 12(2):514-537, 2014.
- [9] I. Sack, B. Beierbach, U. Hamhaber, D. Klatt, and J. Braun. Non-invasive measurement of brain viscoelasticity using magnetic resonance elastography. NMR Biomed., 21(3):265-271, 2008.

