| Project head: | Uwe Bandelow | |
| Staff: | Alexander Pimenov, Markus Kantner (core support) | |
| Funding period: | January 2019 – December 2020 | |
| Application area: | Nano- and optoelectronics (WIAS), Materials, Light, Devices (MATH+) |
Project background
Semiconductor quantum optics is on the leap from the lab to real world applications. The currently unfolding “second quantum revolution” aims at the development of novel quantum technologies that exploit inherent quantum mechanical phenomena like entanglement and quantum superposition for communication and information processing tasks. Many applications, such as eavesdropping-secure encryption methods and optical quantum computers, rely on quantum light sources that emit single photons or entangled photon pairs on demand. Semiconductor quantum dots (QDs) have been identified as ideal optically active elements for such devices as they can be directly integrated into semiconductor-based photonic resonators. In the interest of compactness and scalability, electrical carrier injection is highly desirable, however, simple electrically driven quantum light emitting diodes have severe limitations as they do not allow for resonant excitation and intrinsically suffer from charge noise. This limits the indistinguishability of the emitted photons, which is required for emerging quantum technologies.
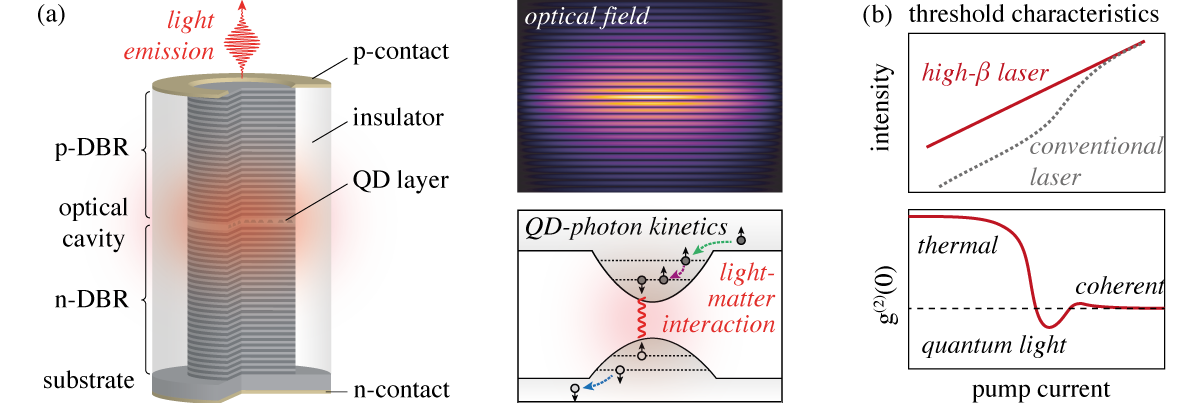
A promising solution to this problem are nanolasers (see Fig. 1), that are ultimately miniaturized coherent light sources, which can act as electrically triggered excitation sources. Such nanolasers employ only a few QDs as gain medium, embedded in a high quality optical micro-resonator with spatial dimensions down to the diffraction limit. This tremendous size reduction takes the concept of lasing to a completely new regime: If light is confined to such a small volume, the light-matter interaction is dominated by cavity quantum electrodynamic (cQED) effects. In this respect, nanolasers operate on the exciting crossroad between quantum light emitters and conventional diode lasers. The exploitation of cQED effects facilitates thresholdless lasing, increased modulation speed and significantly reduced energy consumption (“green photonics”). Beyond their usage in nanophotonic circuits, nanolasers are promising candidates for optical interconnects in data centers and supercomputers, where the demand for high power efficiency has evolved into a pressing economical and ecological problem over the last decade.
While the design principles of optically driven nanolasers are well understood, only little is known in the challenging case of electrically pumped devices. Currently, their improvement relies on heuristic and empirical optimization, which requires a huge employment of resources. The goal of this project is to support the development and optimization of nanolasers for emerging quantum technologies based on advanced mathematical modeling and numerical simulation.
Objectives
This project is focused on advanced mathematical modeling and numerical simulation of nanolasers and their optimization for applications in emerging quantum technologies. The particular goals and methods are described in the following.
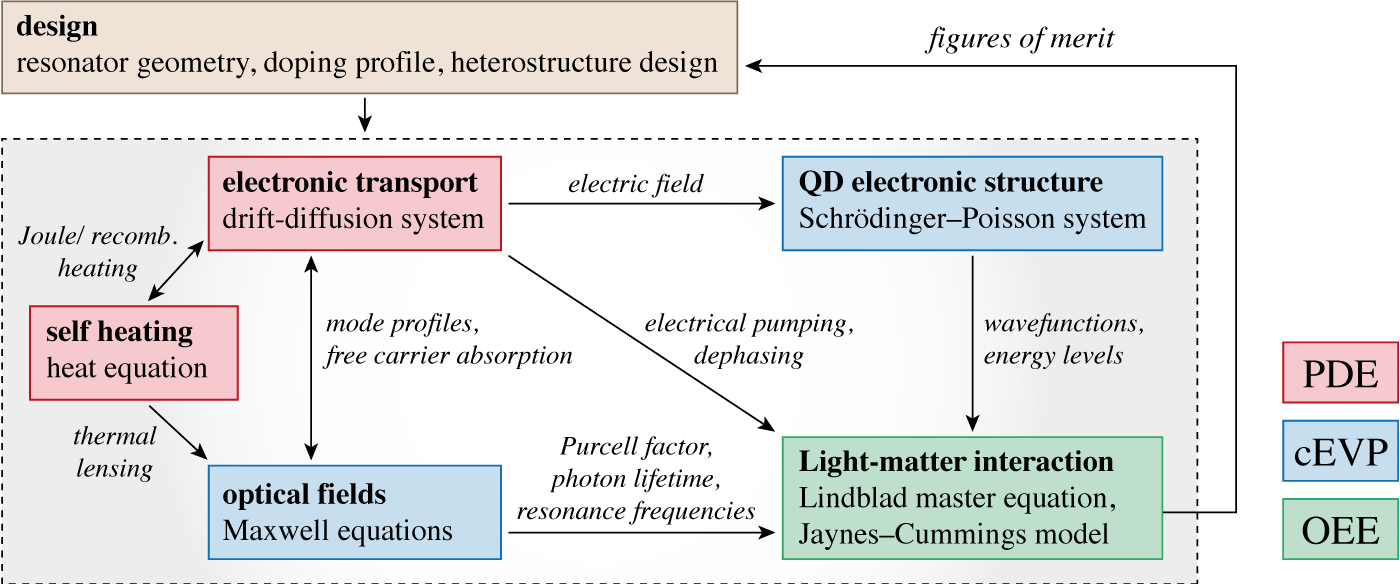
The mathematical modeling of nanolasers is a complex multi-physics problem, which requires a fully quantum mechanical description of the light-matter interaction in the optically active region. We employ a comprehensive hybrid quantum-classical modeling approach, that extends our previous work on single-photon sources and is far beyond standard simulation approaches on conventional laser diodes. It includes aspects of semi-classical transport theory in semiconductors, electromagnetic field theory and cQED in second quantization for the coupled QD-photon system. Mathematically, this involves systems of nonlinear partial differential equations (electronic transport, heat transport), complex non-Hermitian eigenvalue problems (optical fields in microcavities, Schrödinger–Poisson problem for QD electronics) and operator evolution equations for the quantum statistical operator describing the open quantum system (Lindblad master equation, Jaynes–Cummings model). Based on our comprehensive modeling framework, we will investigate the device characteristics under stationary, pulsed and noisy (stochastic) injection conditions.
We will implement a toolchain for the numerical simulation of the model sketched in Fig. 2. This includes state-of-the-art solvers for nonlinear transport problems (finite volumes Scharfetter–Gummel method) and complex non-Hermitian eigenvalue problems (finite element method, perfectly matched layers, collaboration within AA2 with S. Burger) for large 3D problems. For the solution of the quantum optical problem we will employ coupled cluster expansion techniques or tensor network methods to truncate the huge dimensionality of the underlying Hilbert space. We will develop an efficient and robust iteration scheme (multi-scale methods in space and time) for the self-consistent solution of the fully coupled problem (see Fig. 2).
Electrically driven nanolasers require highly efficient electrical carrier injection (low resistance) on the one hand, but a high-quality low-loss optical resonator on the other hand. In order to explore the theoretical performance limits, we address the complex interplay between various physical mechanisms (free carrier absorption, surface recombination, Purcell enhancement). Using problem-adapted optimization techniques and sensitivity analysis, we investigate the optimal configuration of the device parameters (resonator geometry, doping profile, heterostructure design) in view of the laser emission characteristics (modulation response, energy consumption, intensity, coherence).
Collaboration
Internal
Thomas Koprucki, Karsten Tabelow, Jürgen Fuhrmann, Alexander Mielke, Matthias Liero, Annegret Glitzky, Michael Hintermüller, Hans-Jürgen WünscheExternal
Sven Burger (ZIB), Stephan Reitzenstein (TUB), Andreas Knorr (TUB)Project related literature
- M. Kantner: “Generalized Scharfetter–Gummel schemes for electro-thermal transport in degenerate semiconductors using the Kelvin formula for the Seebeck coefficient,” Journal of Computational Physics 402, 109091 (2020). doi: 10.1016/j.jcp.2019.109091
- A. V. Kovalev, P. S. Dmitriev, A. G. Vladimirov, A. Pimenov, G. Huyet and E. A. Viktorov: “Bifurcation structure of a swept-source laser,” Physical Review E 101 (1), 012212 (2020). doi: 10.1103/PhysRevE.101.012212
- U. Gowda, A. Roche, A. Pimenov, A. G. Vladimirov, S. Slepneva, E. A. Viktorov, G. Huyet: “Turbulent coherent structures in a long cavity semiconductor laser near the lasing threshold,” WIAS Preprint no. 2724, Berlin (2020). doi: 10.20347/WIAS.PREPRINT.2724
- M. Heida, M. Kantner, A. Stephan: “Consistency and convergence for a family of finite volume discretizations of the Fokker–Planck operator,” WIAS Preprint no. 2684, Berlin (2020). doi: 10.20347/WIAS.PREPRINT.2684
- M. Kantner and T. Koprucki: “Non-isothermal Scharfetter–Gummel scheme for electro-thermal transport simulation in degenerate semiconductors,” In Finite Volumes for Complex Applications IX, Eds.: R. Klöfkorn R., E. Keilegavlen, F. Radu and J. Fuhrmann. Springer Proceedings in Mathematics and Statistics, Vol. 323, pp. 173–182, Springer, Cham (2020) doi: 10.1007/978-3-030-43651-3_14
- M. Kantner: “Electrically Driven Quantum Dot Based Single-Photon Sources: Modeling and Simulation.” Springer Theses, Springer, Cham (2020) doi: 10.1007/978-3-030-39543-8
- U. W. Pohl, A. Strittmatter, A. Schliwa, M. Lehmann, T. Niermann, T. Heindel, S. Reitzenstein, M. Kantner, U. Bandelow, T. Koprucki, H.-J. Wünsche: “Stressor-Induced Site Control of Quantum Dots for Single-Photon Sources,” In Semiconductor Nanophotonics, Chap. 3, pp. 53–90, Eds.: M. Kneissl, A. Knorr, S. Reitzenstein and A. Hoffmann, Springer (2020) doi: 10.1007/978-3-030-35656-9_3
- M. Kantner, T. Höhne, T. Koprucki, S. Burger, H.-J. Wünsche, F. Schmidt, A. Mielke and U. Bandelow: “Multi-dimensional modeling and simulation of semiconductor nanophotonic devices,” In Semiconductor Nanophotonics, Chap. 7, pp. 241–283, Eds.: M. Kneissl, A. Knorr, S. Reitzenstein and A. Hoffmann, Springer (2020) doi: 10.1007/978-3-030-35656-9_7
- S. Rodt, P.-I. Schneider, L. Zschiedrich, T. Heindel, S. Bounouar, M. Kantner, T. Koprucki, U. Bandelow, S. Burger and S. Reitzenstein: “Deterministic quantum devices for optical quantum communication,” In Semiconductor Nanophotonics, Chap. 8, pp. 285–359, Eds.: M. Kneissl, A. Knorr, S. Reitzenstein and A. Hoffmann, Springer, Cham (2020) doi: 10.1007/978-3-030-35656-9_8
- M. Kantner, T. Koprucki, H.-J. Wünsche and U. Bandelow: “Simulation of quantum dot based single-photon sources using the Schrödinger–Poisson-Drift-Diffusion-Lindblad system,” Proc. of the 24th International Conference on Simulation of Semiconductor Processes and Devices (SISPAD 2019), Ed.: F. Driussi, pp. 355–358 (2019) doi: 10.1109/SISPAD.2019.8870459
- M. Kantner: “Simulation of quantum light sources using the self-consistently coupled Schrödinger–Poisson-Drift-Diffusion-Lindblad system,” Proc. of the 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Eds.: J. Piprek, K. Hinzer, pp. 15–16 (2019) doi: 10.1109/NUSOD.2019.8806869
- M. Kantner: “A generalized Scharfetter–Gummel scheme for degenerate and non-isothermal semiconductors,” Proc. of the 19th International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Eds.: J. Piprek, K. Hinzer, pp. 7–8 (2019) doi: 10.1109/NUSOD.2019.8806839
- M. Kantner, M. Mittnenzweig, A. Mielke and N. Rotundo: “Mathematical modeling of semiconductors: From quantum mechanics to devices.” In Topics in Applied Analysis and Optimisation: Partial Differential Equations, Stochastic and Numerical Analysis, Eds.: M. Hintermüller and J. Rodrigues, pp. 269–293, Springer, Cham (2019). doi: 10.1007/978-3-030-33116-0_11
- M. Kantner: “Hybrid modeling of quantum light emitting diodes: Self-consistent coupling of drift-diffusion, Schrödinger–Poisson and quantum master equations,” Proc. SPIE Vol. 10912, Physics and Simulation of Optoelectronic Devices XXVII, 109120U (2019). doi: 10.1117/12.2515209
- M. Kantner, M. Mittnenzweig and T. Koprucki: “Hybrid quantum-classical modeling of quantum dot devices,” Phys. Rev. B 96, 205301 (2017). doi: 10.1103/PhysRevB.96.205301
- P. Farrell, N. Rotundo, D. H. Doan, M. Kantner, J. Fuhrmann and T. Koprucki: “Mathematical Methods: Drift-Diffusion Models,” in Handbook of Optoelectronic Device Modeling and Simulation (Ed. J. Piprek), Vol. 2, Chap. 50, pp. 731–771, CRC Press (2017) doi: 10.4324/9781315152318-25
- M. Kantner and T. Koprucki: “Numerical simulation of carrier transport in semiconductor devices at cryogenic temperatures,” Opt. Quant. Electron. 48, 543 (2016). doi: 10.1007/s11082-016-0817-2
- M. Kantner, U. Bandelow, T. Koprucki, J.-H. Schulze, A. Strittmatter and H.-J. Wünsche: ”Efficient Current Injection Into Single Quantum Dots Through Oxide-Confined PN-Diodes,“ IEEE Trans. Electron Dev. 63, 2036–2042 (2016). doi: 10.1109/TED.2016.2538561


