Matheon Project C9: Simulation and Optimization of Semiconductor Crystal Growth from the Melt Controlled by Traveling Magnetic Fields
(Project was called "Numerical simulation and control of sublimation growth of semiconductor bulk single crystals" during the second funding period (-05/2010) of the DFG Research Center Matheon "Mathematics for Key Technologies".)- Quick-Links
Research Team, Collaboration, Funding
- Head Persons of Research Team
-
Prof. Dr. Jürgen Sprekels,
Dr. Olaf Klein
(Weierstrass Institute for Applied Analysis and Stochastics (WIAS), Berlin, Germany),
Prof. Dr. Fredi Tröltzsch
(Department of Mathematics, Technical University (TU), Berlin, Germany). - Current Research Team and Topical Classification
-
Dr. Pierre-Etienne Druet,
Dr. Olaf Klein,
Prof. Dr. Jürgen Sprekels,
Prof. Dr. Fredi Tröltzsch,
Dr. Irwin Yousept,
Vili Dhamo (associated member).
Pierre-Etienne Druet, Olaf Klein, and Jürgen Sprekels are members of the research group Thermodynamic Modeling and Analysis of Phase Transition at WIAS;
Fredi Tröltzsch, Irwin Yousept and Vili Dhamo are members of the research group Modelling - Numerics - Differential Equations, Section: Optimization in PDEs at the Department of Mathematics of TU Berlin.
At WIAS, this project belongs to the application Crystal Growth, Especially under the Influence of Magnetic Fields in the Main Application Area Phase Transitions and Multi-functional Materials.
At Matheon, this project belongs to the Domains of Expertise Energy in the Application area C: Production. -
Related Projects:
- In Collaboration With
- Leibniz Institute of Crystal Growth (IKZ), Berlin, Germany
- Funding
- This project is currently supported by the
Deutsche Forschungsgemeinschaft (DFG)
within the
DFG Research Center Matheon "Mathematics for Key Technologies".

Crystal Growth Techniques
Semiconductor crystals like silicon (Si), silicon carbide (SiC), gallium arsenide (GaAs), and aluminum nitride (AlN) crystals have important applications in key technologies.
Industrial applications of these semiconductor crystals require the availability of large-diameter, low-defect crystals, and a high growth rate during the production process is desirable to reduce production time and costs.
-
The most important industrial technique for growth of Si and GaAs bulk single crystals is the growth from the melt, especially by the Czochralski method and their variants, i.e. Liquid Encapsulated Czochralski (LEC) and Vapor pressure controlled Czochralski (VCz).
In this kind of processes, a rotating crystal seed is dipped into the melt that is contained in a rotating crucible. The seed is then slowly pulled out of the melt, and a single crystal solidifies. Since the melt flow is turbulent, impurities may find their way into the growing crystal, and temperature oscillations with small frequencies may occur below the crystal. This should be avoided, since this would lower the quality of the grown crystal.
To achieve this aim, one applies time-dependent electromagnetic fields to the melt, which is electrically conducting so that a Lorentz force is induced into it in their presence. This Lorentz force can be used to influence the melt motion.
-
The state-of-the-art procedure for the production of SiC and AlN bulk single crystals is the Physical Vapor Transport (PVT) (also called Modified Lely Method), which involves sublimation of the source material. Even though substantial progress has been made in recent years, the technological problems remain challenging, and only partial solutions exist.
From 2002 to 2007, C9 dealt with modeling, simulating and optimizing the production of SiC and AlN bulk single crystals by PVT. These investigations were finished successfully both from the mathematical and the industrial viewpoint; the software WIAS-HiTNIHS developed in C9 was licensed to IKZ.
Further informations about activities on modeling and optimal control of sublimation growth can be found here.
This project is carried out in close cooperation with the Leibniz Institute of Crystal Growth (IKZ) in Adlershof.
Crystal Growth from the Melt
In 2007, C9 shifted its efforts to model variants of the Czochralski growth of bulk semiconductor crystals from the melt. The reason for this was that the use of traveling magnetic fields (TMF), a special kind of time-dependent magnetic fields to control the turbulent melt flow, has drawn increasing attention from crystal growing industry worldwide.
The interest in these problems was triggered by the project KRISTMAG of the Technologiestiftung Berlin (TSB). In this project, a WIAS group headed by O. Klein and J. Sprekels joined forces with IKZ and two industrial partners. A technological breakthrough was achieved by demonstrating that traveling magnetic fields can be successfully applied for this task. A special heater magnet module (HMM) was developed, and a number of patent applications were filed. The groundbreaking nature of these developments was recognized by the Innovationspreis (innovation prize) Berlin-Brandenburg 2008. The software WIAS-HiTNIHS played an important role in these investigations.
To model and simulate crystal growth from the melt unter the influence of TMFs, a PDE system modeling temperature-dependent magnetohydrodynamics coupled to the energy balance has been derived.
The PDE system features the following components:
- Maxwell's equations for the electromagnetic field,
- nonlinear heat equation, coupled to nonlocal radiation boundary conditions,
- a complicated domain composed of a multitude of subdomains having different material properties,
- strongly temperature-dependent and anisotropic physical coefficients,
- Boussinesq approximation of the Navier-Stokes equations for modeling thermally and electrically conducting fluids.
In a addition to modeling and performing simulations, one has to establish existence and uniqueness for solutions to this PDE system and one has to solve an optimal control problem for this PDE system with pointwise state and control constraints.
In accordance with the needs of our partners, we study optimal control problems arising from the use of traveling magnetic fields to influence melt flow during crystal growth from the melt. Issues of special interest are:
- Eddies in the melt flow should have a suitable form to keep impurities apart from the growing crystal.
- The amplitudes of temperature oscillations below the crystals should be minimized, while their frequencies must be kept sufficiently large.
- The solid-liquid interface ("free boundary") should have a special form in order to grow crystals of high quality.
Hence, one has to deal with new classes of control and state constrained optimization problems for the very difficult PDE system described above.
Analytical aspects of the PDE system
A mathematical breakthrough of considering the PDE system described above was achieved in the thesis by P.-E. Druet, who showed existence for this system. The Leibniz Association bestowed the Nachwuchspreis 2010 der Leibniz-Gemeinschaft in Naturwissenschaften und Technik on him for his dissertation, see press release 18/2010 of the Leibniz Association. In the stationary case, existence of weak solutions was obtained, and the uniqueness for small data; for the transient problem, a defect measure concentrated on the boundary of the heaters appears in the solution. Uniqueness follows only for strong solutions.
Corner stones of these results are, on the one hand, the advances made on the analysis of the nonlocal radiation operators in low-regularity situations; on the other hand, they rely on new regularity results for the Maxwell system that also play an important role in the treatment of optimal control problems.
Optimal control of the PDE system
To rigorously deal with optimal control problems related to the heating of the growth apparatus and the achievement of certain flow properties, we have to deal with PDE system described above, i.e., the complex coupled system of partial differential equations consisting of the Maxwell system, the Navier-Stokes system, and the heat equation with nonlocal and nonlinear terms,
Following the plans for the current funding period, and in accordance with the needs of our partners from IKZ and industry, we have studied optimal control problems arising from the use of traveling magnetic fields to influence the melt flow during crystal growth from the melt.
While good advance (see below) was made within the report period in general optimal control theory and the investigation of the solid-liquid free boundary, the problems concerning the occurrences of eddies in the melt flow and of the temperature oscillations have not yet been settled and will be studied later this funding period.
The groundbreaking existence results established in the thesis by P.-E. Druet, also paved the way for a mathematical analysis of control problems. However, as described above, the mathematical model for heating the melt is very complex; in particular, all equations are quasilinear. Consequently, it is currently far too ambitious to make an attempt to tackle optimal control problems for this system in its full generality. We therefore analyzed and numerically treated simplified versions thereof, with increasing degree of complexity and mathematical difficulty.
The analysis of necessary and sufficient optimality conditions was carried out for a coupled system consisting of a semilinear heat equation and Maxwell's equations. Moreover, an analysis of time-optimal control problems for linear evolution Maxwell equations was developed that applies to the optimal switching between magnetic fields of different polarization.
Also, in joint work with E. Casas, the difficulties arising from quasilinear equations were studied for the optimal control of quasilinear elliptic equations. We discovered that already this comparatively simple case leads to a highly technical analysis. An extension to systems of quasilinear systems of evolution equations will have to be substantially more complicated and technically delicate.
An optimal control problem of induction heating type with state constraints was solved numerically in a 3D domain. The problem was modeled by a weakly coupled nonlinear system for temperature and magnetic field.
Free Boundary
Moreover, important goals for crystal growth are the proximity of the solid-liquid interface to a desired interface or a slightly convex shape. Hence, it is very desirable that the solid-liquid interface itself, a free boundary, becomes part of the objective functional. Relevant model equations for the interface are the Stefan condition or the Stefan-Gibbs-Thomson condition
Anisotropic extensions of this relation can also be considered In a model for the crystal-melt system as part of a crystal growth system under study in this project, the temperature satisfies a stationary heat equation within the melt and a stationary heat equation with a different value for the heat conductivity in the crystal, coupled with continuity for the heat fluxes and a Stefan-Gibbs-Thomson condition.
New regularity results for this transmission problem could be proved, which guarantee that the classical formulation of this free boundary problem is well posed provided that the discontinuity of the heat conductivity on the interface is a small perturbation.
The Simulation Software and Simulation Results
The following software packages were licensed to the Leibniz Institute of Crystal Growth (IKZ).
-
WIAS-HiTNIHS (P. Philip and O. Klein) WIAS-HiTNIHS is a simulation tool for stationary and transient temperature distributions in axisymmetric technical systems that are subject to intense heating. The simulator accounts for heat transfer by radiation through cavities and allows for temperature-dependent material parameters and anisotropic thermal conductivity. It can be used to compute traveling magnetic fields and the resulting Lorentz forces acting on conducting liquids. WIAS-HiTNIHS was one of the foundations of the project KRISTMAG. and has also been used within the project AVANTSOLAR, see below
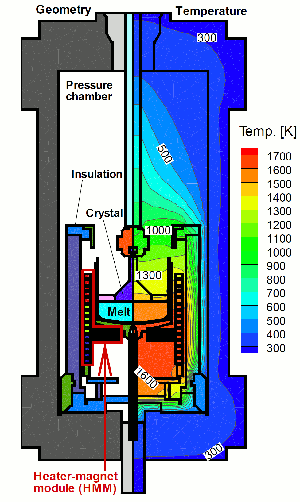
See description of WIAS-HiTNIHS for more informations.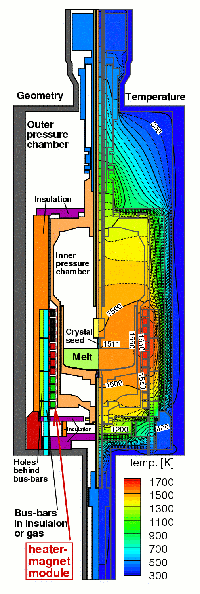
Configurations of Czochralski Type Growth Processes used for for growing GaAs crystals and corresponding temperature distributions computed by WIAS-HiTNIHS within the project KRISTMAG.
-
Left hand side: Vapor pressure controlled Czochralski (VCz)
-
Right hand side: Liquid Encapsulated Czochralski (LEC) with heater magnet module (HMM) following patent EP 2 162 571 B1 / DE patent 10 2007 028 548
-
-
WIAS-MatConE (O. Klein) WIAS-MatConE is a tool to provide prototypical GUIs for creating and editing files that are used as inputs for simulation software. Typical examples are material data files and control files. WIAS-MatConE provides a fast and flexible way to generate GUIs for prototypical software without having to deal with the details of GUI development.
In the years 2008-2011, the partners of the KRISTMAG-project joined forces with the SCHOTT Solar Wafer GmbH and two other research institutes for the project AVANTSOLAR, which was again funded by the Technologiestiftung Berlin (TSB). This project has dealt with using traveling magnetic fields to improve the growth of silicon for solar cells from the melt.
Within this project (in which none of the Matheon-paid researchers took part) the software package WIAS-HiTNIHS developed in the project C9 was used to compute temperature distribution and electromagnetic fields within an industrial directional solidification furnace for solar silicon.
Moreover, for a reduced model, which only comprises the energy balance with heat transport via radiation, an optimization problem was formulated that aims at choosing the heating powers applied to the different coils of the HMM to adjust the temperature values in some chosen points. This problem was formulated as a least squares problem with constraints for the applied powers. It was solved numerically by a combination of a modified Newtown method and of the method of steepest descent, using the antigradient as search direction.
Current and Future Tasks
Now that important questions of numerical analysis for optimal control problems related to our industrial background are settled, the applicability of the developed optimal control techniques will have to be confirmed for a model that is reasonably close to the real configuration, yet not overloaded with too many technical details. In the remainder of the funding period, we plan to determine traveling magnetic fields that drive the melt flow in an optimal way. Within the projects KRISTMAG and AVANTSOLAR, it has been shown that the melt can be strongly influenced by controlled traveling magnetic fields. However, a numerical treatment of the problem of optimizing melt flows has not yet been done.
Challenges for dealing with the optimization problem lie in the fact that one still has to consider pointwise state constraints and that the regularity theory of the forward problem will probably have to be improved. Even more challenging is the step of controlling the full system, including the hydrodynamic component, which is, ultimately, the goal from the point of view of the application. A subproblem lies in a suitable formulation of objective functionals that reflect the aim of reducing the amplitude while increasing the frequency of temperature oscillations in the vicinity of the growing crystal. Control parameters are given by the time-dependent heating power and by the time-dependent phase shifts between different induction coils.
From the point of view of the analysis, our plan is to continue the investigation of the free boundary problem for the solidification interface. We want to study the optimal control problem for the curvatures of the interface (slightly convex shape) in the situation that the temperature satisfies a stationary heat equation.
Publications
The following list restricts to the publications on crystal growth from the melt. The publications concerning the former topic of project C9, sublimation growth, are listed on the subpage sublimation growth of the project.Theses
-
W. Dhamo: Optimal boundary control of quasilinear partial differential equations: theory and numerical analysis. Doctoral thesis, Technical University of Berlin, Germany, submitted January 2012.
-
P-E. Druet: Analysis of a coupled system of partial differential equations modeling the interaction between melt flow, global heat transfer, and applied magnetic fields in crystal growth. Doctoral thesis, successfully defended at the Department of Mathematics, Humboldt University of Berlin, Germany, February, 2009.
Using the following link, you can download the thesis: thesis by P.-E. Druet
Submitted Articles
-
W. Dreyer, P.-E. Druet, O.Klein, J.Sprekels: Mathematical modeling of Czochralski type growth processes for semiconductor bulk single crystals, 2012.
The preprint of this article is available at Matheon Preprint 929 .
-
P.-E. Druet: Global Lipschitz continuity for elliptic transmission problems with a boundary intersecting interface, 2010.
The preprint of this article is available at Matheon Preprint 741 .
-
P.-E. Druet: The classical solvability of the contact angle problem for generalized equations of mean curvature-type, 2010.
The preprint of this article is available at Matheon Preprint 745 .
-
K. Altmann, S. Stingelin, F. Tröltzsch: On some optimal control problems for electric circuits, Int. Journal of Circuit Theory, submitted 20. Oct. 2010.
The preprint of this article is available at Matheon Preprint 959 .
Articles in Refereed Journals
-
P-E. Druet, O.Klein, J.Sprekels, F.Tröltzsch, I.Yousept: Optimal control of 3D state-constrainded induction heating problems with nonlocal radiation effects, SIAM Journal Contr. Optim., 49(2011), 1707-1736.
The preprint of this article is available at Matheon Preprint 579 .
-
I. Yousept: Optimal control of Maxwell's equations with regularized state constraints, Computational Optimization and Applications, 2011. Published online
-
F. Tröltzsch, I. Yousept: PDE-constrained optimization of time-dependent 3D electromagnetic induction heating by alternating voltages, ESAIM: M2AN, 2011. Published online
-
P. Merino, I. Neitzel, F. Tröltzsch: On linear-quadratic elliptic control problems of semi-infinite type, Applicable Analysis, 90(2011), 1047-1074.
-
P-E Druet, P. Philip: Noncompactness of integral operators modeling diffuse-gray radiation in polyhedral and transient settings , Integr. Equ. Oper. Theory, 69(2011), 101-111.
The preprint of this article is available at Matheon Preprint 740 .
-
E. Casas, F. Tröltzsch: A general theorem on error estimates with application to a quasilinear elliptic optimal control problem, Computational Optimization and Applications. Published online first
The preprint of this article is available at Matheon Preprint 961 .
-
E. Casas, F. Tröltzsch: Numerical analysis of some optimal control problems governed by a class of quasilinear elliptic equations, ESAIM: COCV, 17(2011), 771-800.
-
V. Dhamo and F. Tröltzsch: Some aspects of reachability for parabolic boundary control problems with control constraints , Computational Optimization and Applications, 50(2011), 75-110.
The preprint of this article is available at Matheon Preprint 551 .
-
I. Yousept: Optimal control of a nonlinear coupled electromagnetic induction heating system with pointwise state constraints, Mathematics and its Applications/Annals of AOSR, 2(2010), 45-77.
-
F. Tröltzsch: On finite-elemente error estimates for optimal control problems with elliptic PDEs, in I. Lirkov, S. Margenov and J. Wasniewski editors, Large Scale Scientific Computing, Lecture Notes in Computer Science, Springer, vol 5910(2010), 40-53.
-
P. Merino, F. Tröltzsch, B. Vexler: Error estimates for the finite-element approximation of a semilinear elliptic control problem with state contraints and finite dimensional control space, ESAIM: Mathematical Modeling and Numerical Analysis, 44(2010), 167-188.
-
P. Merino, I. Neitzel, F. Tröltzsch: Error estimates for the finite-element discretization of semi-infinite elliptic control problems, Discussiones Mathematica, 30(2010), 221-236.
-
M. Hinze, F. Tröltzsch: Discrete concepts versus error analysis in PDE-constrained optimization, GAMM-Mitteilungen, 33(2010), 148-162.
-
E. Casas, F. Tröltzsch: Recent advances in the analysis of pointwise state-constrained elliptic control problems, ESAIM: COCV, 16(2010), 581-600.
-
P-E Druet: Weak solutions to a time-dependent heat equation with nonlocal radiation boundary condition and arbitrary p-summable right-hand side, Applications of Mathematics, 55(2010), 111-149.
-
M. Hintermüller, I. Yousept: A sensitivity-based extrapolation technique for the numerical solution of state-constrained optimal control problems, ESAIM COCV, 16(2010), 503-522.
The preprint of this article is available at Matheon Preprint 421 .
-
O. Klein, Ch.Lechner, P-E.Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F-M. Kießling, W. Miller, U. Rehse, P. Rudolph: Numerical simulations of the influence of a traveling magnetic field, generated by an internal heater-magnet module, on liquid encapsulated Czochralski crystal growth, Magnetohydrodynamics, (45)2009, 557-567.
-
P-E Druet: Existence for the stationary MHD-equations coupled to heat transfer with nonlocal radiation effects , Cz. Math. J., 59(2009), 791-825.
-
E. Casas, F. Tröltzsch: First- and second-order optimality conditions for a class of optimal control problems with quasilinear elliptic equations, SIAM J. Control and Optimization, 48(2009), 688-718.
The preprint of this article is available at Matheon Preprint 474 .
-
C. Meyer, I. Yousept: Regularization of state-constrained elliptic optimal control problems with nonlocal radiation interface conditions, Comput. Optim. Appl., online published first .
-
C. Meyer, I. Yousept: State-constrained optimal control of semilinear elliptic equations with nonlocal radiation inteface conditions, SIAM J. on Control and Optimization, 48 (2009), 734-755.
-
F. Tröltzsch, I. Yousept: Source representation strategy for optimal boundary control problems with state constraints , J. Analysis and its Applications, 28 (2009), 189-203.
-
F. Tröltzsch, I. Yousept: A regularization method for the numerical solution of elliptic boundary control problems with pointwise state constraints, Comput. Optim. Appl., 42 (2009), 43-63.
-
P-E Druet, J. Naumann: On the existence of weak solutions to a stationary one-equation RANS model with unbounded eddy viscosities, Ann. Univ. Ferrara, 55 (2009), 67-87.
-
P-E Druet: Existence of weak solutions to the time-dependent MHD-equations coupled to heat transfer with nonlocal radiation boundary conditions, Nonlinear Analysis. Real World Applications, 10 (2009), 2914-2936.
-
P-E Druet: Weak solutions to a stationary heat equation with nonlocal radiation boundary condition and right-hand side in L-p (p>=1), Math. Meth. Appl. Sci., 32 (2009), 135-166.
-
J-C. de los Reyes, I. Yousept: Regularized state-constrained boundary optimal control of the Navier-Stokes equations, J. Math. Anal. Appl., 356 (2009), 257-279.
-
E. Casas, J-C de los Reyes, F. Tröltzsch: Sufficient second order optimality conditions for semilinear control problems with pointwise state constraints, SIAM J. Control and Optimization, 47(2008), 616-643.
The preprint of this article is available at Matheon Preprint 473 .
-
J-C. de los Reyes, P. Merino, J. Rehberg, F. Tröltzsch: Optimality conditions for state-constrained PDE control problems with time-dependent controls, Control and Cybernetics, 37(2008), 7-38.
The preprint of this article is available at Matheon Preprint 472 .
-
M. Hintermüller, I. Yousept: Mesh independence of semismooth Newton methods for Lavrentiev-regularized state constrained optimal control problems, Numerische Mathematik, 108 (2008), 571-603.
-
O. Klein, F. Luterotti, R. Rossi: Existence and asymptotic analysis of a phase field model for supercooling, Quarterly of Applied mathematics, 64 (2006), 291-319.
Articles in Conference Issues of Refereed Scientific Journals
-
N. Dropka, W. Miller, U. Rehse, P. Rudolph, F. Buellesfeld, U. Sahr, O. Klein, D. Reinhardt: Numerical study on improved mixing in silicon melts by double-frequency (TMF), J. Crystal growth, 318 (2011), 275-279. (Proceedings volume for the 16th International Conference on Crystal Growth (ICCG-16), August 2010, Beijing, China)
-
O. Klein, Ch. Lechner, P-E. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F-M. Kießling, W. Miller, U. Rehse, P. Rudolph: Numerical simulation of Czochralski crystal growth under the influence of a traveling magnetic field generated by an internal heater-magnet module (HMM), J. Crystal growth, 310 (2008), 1523-1532. (Proceedings volume for the 15th International Conference on Crystal Growth (ICCG-15), August 12-17, 2007, Salt Lake City, USA.)
-
O. Klein, Ch. Lechner, P-E. Druet: Development of a software for the numerical simulation of VCz growth under the influence of a traveling magnetic field, J. Crystal growth, 303 (2007), 161-164. (Proceedings volume for the 5th International Workshop on "Modeling in Crystal Growth" (IWMCG-5), September 10 - 13, 2006, Bamberg, Germany.)
Articles in Conference Proceedings and Collections
-
P-E Druet: Weak solutions to a model for crystal growth from the melt in changing magnetic fields, In Optimal Control of Coupled Systems of PDE, K. Kunisch, G. Leugering, J. Sprekels, F. Tröltzsch editors, Birkhäuser, Basel, International series of numerical mathematics, vol. 158, 2009, 123-137.
-
P. Rudolph, Ch. Frank-Rotsch, F-M. Kießling, W. Miller, U. Rehse, O. Klein, Ch. Lechner, J. Sprekels, B. Nacke, H. Kasjanow, P. Lange, M. Ziem, B. Lux, M. Czupalla, O. Root, V. Trautmann, G. Bethin: Crystal growth in heatermagnet modules - from concept to use, In Procedings of the International Scientific Colloquium Modelling for Electromagnetic Processing (MEP2008), E. Baacke and B. Nacke editors, Leibniz University of Hannover, 2008, 79-84.
The text of this article is available at http://www.modlab.lv/publications/MEP2008/pdfs/91-96.pdf.
-
O. Klein, Ch. Lechner, P-E. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F-M. Kießling, W. Miller, U. Rehse, P. Rudolph: Numerical simulations of the influence of a traveling magnetic field, generated by an internal heater-magnet module, on Czochralski crystal growth, In Procedings of the International Scientific Colloquium Modelling for Electromagnetic Processing (MEP2008), E. Baacke and B. Nacke editors, Leibniz University of Hannover, 2008, 91-96.
The text of this article is available at http://www.modlab.lv/publications/MEP2008/pdfs/103-108.pdf.
-
J-C. de los Reyes and I. Yousept: Boundary optimal flow control with state constraints, Proc. Appl. Math. Mech., 2007. Published online
The preprint of this article is available at Matheon Preprint 422 .
Miscellaneous Articles
-
M. Czupalla, F.-M. Kießling, O. Klein, R.-P. Lange, B. Lux, W. Miller, P. Rudolph, M. Ziem, F. Kirscht: Verfahren und Vorrichtung zur Züuchtung von Kristallen aus elektrisch leitenden Schmelzen, die in der Diamant- oder Zinkblendestruktur kristallisieren, Offenlegungschrift (Invention Disclosure) of patent application DE 10 2009 027 436 A1, German Patent and Trade Mark Office, January 13th, 2011.
-
Ch. Frank-Rotsch, P. Rudolph, O. Klein, R-P. Lange, B. Nacke: Vorrichtung und Verfahren zur Herstellung von Kristallen aus elektrisch leitenden Schmelzen (Device and Method for Producing Crystals from Electroconductive Melt) , Patentschrift (patent specification) of granted european patent EP 2 162 571 B1 (associated to granted german patent DE 10 2007 028 548), European Patent Office, Dez. 21st, 2011.
-
Ch. Frank-Rotsch, P. Rudolph, O. Klein, R-P. Lange, B. Nacke: Vorrichtung und Verfahren zur Herstellung von Kristallen aus elektrisch leitenden Schmelzen (Device and Method for Producing Crystals from Electroconductive Melt) , Patentschrift(patent specification) of granted patent DE 10 2007 028 548, German Patent and Trade Mark Office, July, 17th, 2009.
-
P-E Druet: Higher integrability of the Lorentz force for weak solutions to Maxwell's equations in complex geometries, Preprint No. 1270, Weierstrass Institute for Applied Analysis and Stochastics (WIAS), Berlin, Germany.
The preprint is available at Wias Preprint 1270 .
Presentations
The following list restricts to the presentations on crystal growth from the melt. The presentations about sublimation growth, the former topic of Project C9, are listed on the subpage sublimation growth of the project.International Conference Plenary Lectures and International Courses
-
J. Sprekels: Mathematical challenges in the industrial growth of semiconductor bulk crystals, 3rd International Riemann School of Mathematics, Verbania, Italy, 26/09/2011.
-
F. Tröltzsch: On some optimal control problems of electromagnetic fields, SIAM Conference on optimization, Darmstadt, Germany, 17/05/2011.
-
J. Sprekels: Optimal control of PDEs, Summer school (Short course, 4 lectures), Cortona, Italy, 12-17/07/2010.
-
F. Tröltzsch: Process control in magnetohydrodynamics, Workshop Coupled PDEs in multiphysics, Castro Urdiales, 23/06/2010.
-
J. Sprekels: Problems in the industrial growth of semiconductor crystals: Radiative heat transfer, convection, magnetic fields and free boundaries, Conference The legacy of John Crank - Developments in Time Dependent PDE's, Diffusion and Free Boundary Problems, Brunel University, Uxbridge, 07/10/2008.
Talks
-
J. Sprekels: Mathematical challenges in the industrial growth of semiconductor bulk single crystals, Universität Erlangen, 13/01/2012.
-
I. Yousept: Optimal control of Maxwell's system, MATHEON Workshop on Optimization with PDE constraints, Berlin, 19/12/2011.
-
I. Yousept: Optimal control of Maxwell's equations and its applications, Workshop on Optimal Control of Partial Differential Equations, Klaffenbach, Chemnitz, 31/11/2011.
-
F. Tröltzsch: A general theorem on error estimates with application to optimal control, International Workshop on Control and Optimization of PDEs, Graz, 10/10/2011.
-
I. Yousept: Control of Maxwell's equations, IFIP 2011, Berlin, 16/09/2011.
-
F. Tröltzsch: A posteriori error estimation for nonlinear parabolic boundary control, MMAR 2011, Miedzyzdroje, 23/08/2011.
-
F. Tröltzsch: On an optimal magnetization problem, Sino-German Workshop on Optimization, Modeling, Methods and Applications in Industry and Management, Konrad Zuse Center Berlin, 15/08/2011.
-
F. Tröltzsch: Optimality conditions and numerical solution for an optimal magnetization problem, ICIAM 2011, Vancouver, 22/07/2011.
-
I. Yousept: Optimal control of 3D induction heating, ICIAM 2011, Vancouver, 21/07/2011.
-
J. Sprekels: Real-life crystal growth: turbulence, magnetic fields, heat transfer via radiation, and free boundaries, Conference ''Interfaces and discontinuities in solids, liquids and crystals'' (INDI2011), Gargnano, 21/06/2011.
-
P-E Druet: Existence and regularity results for the equations of MHD in complex geometries, TU Darmstadt, 14/06/2011.
-
J. Sprekels: Technological and mathematical problems in the industrial growth of semiconductor bulk single crystals, Workshop ''Nonlinear diffusion: Algorithms, Analysis and Applications'', University of Warwick, 06/06/2011.
-
F. Tröltzsch: Aspects of numerical analysis in the optimal control of nonlinear PDEs, Workshop Inverse Problems and Optimal Control of PDEs, Warwick Institute of Mathematics, 25/05/2011.
-
F. Tröltzsch: Aspects of numerical analysis of elliptic optimal control problems, Workshop on Functional Analysis and Operator Theory, Altenberg, 01/04/2011.
-
J. Sprekels: Mathematical problems in industrial crystal growth: radiation, magnetic fields, and free boundaries, Czech Academy of Sciences, Prag, 15/03/2011.
-
F. Tröltzsch: A posteriori error estimation for nonlinear PDE constrained optimization with application to POD, Workshop on Model Order Reduction in Optimization and Control with PDEs, WIAS Berlin, 28/01/2011.
-
J. Sprekels: Mathematical problems in industrial crystal growth: radiation, magnetic fields, and free boundaries, Symposium zur Angewandten Mathematik anlässlich des 100. Geburtstags von L. Collatz, Universität Hamburg, 07/10/2010.
-
F. Tröltzsch: Some results in the optimal control of electro-magnetic fields, European Multi-Grid Conference EMG 2010, Ischia, 21/09/2010.
-
O. Klein: Modeling and simulations for directional solidification of solar-grade silicon under the influence of traveling magnetic fields, 16th International Conference on Crystal Growth (ICCG-16), Beijing, 10/08/2010.
-
F. Tröltzsch: Some aspects of numerical analysis for the optimal control of quasilinear partial differential equations, Summer School and Workshop on Analysis and Numerics of PDE Constrained Optimization, Lambrecht, 20/07/2010.
-
F. Tröltzsch: Numerical analysis of nonlinear elliptic optimal control problems of semi-infinite type, Workshop ''Nonlinear Optimization, Variational Inequalities and Equilibrium Problems'', Erice, 08/07/2010.
-
O. Klein (joined work with P.-E. Druet, J. Sprekels, Ch. Lechner (Vienna), P. Philip (LMU Munich), Ch. Frank-Rotsch, F.-M. Kießling, W. Miller, U. Rehse, P. Rudolph (IKZ, Berlin): Numerical simulation of the use of traveling magnetic fields to stabilize crystal growth from the melt, Warsaw Seminar on Industrial Mathematics (WSIM'10), Warsaw, Poland, 18/03/2010.
-
O. Klein (joined work with P.-E. Druet, J. Sprekels, Ch. Lechner (Vienna), P. Philip (LMU Munich), Ch. Frank-Rotsch, F.-M. Kießling, W. Miller, U. Rehse, P. Rudolph (IKZ, Berlin): Numerical simulation of Czochralski crystal growth stabilized by a traveling magnetic field generated by an internal heater-magnet module (HMM), EUROTHERM 84 - ''Thermodynamics of Phase Changes'', Namur, Belgium, 25/05/2009.
-
O. Klein (joined work with P.-E. Druet, J. Sprekels, Ch. Lechner (Vienna), P. Philip (LMU Munich), Ch. Frank-Rotsch, F.-M. Kießling, W. Miller, U. Rehse, P. Rudolph (IKZ, Berlin): Modellierung und Simulation der LEC GaAs Züchtung in Heizer-Magnetmodulen, 10. DGKK Kinetik-Seminar joinded with 6. DGKK Workshop "Angewandte Simulation in der Kristallzüchtung", Postdam, Germany, 02/04/2009.
-
F. Tröltzsch: On the verification of bang-bang properties for parabolic boundary control problems, Oberwolfach, Germany, 27/01/2009.
-
O. Klein (et al.): Numerical simulations of the influence of a traveling magnetic field, generated by an internal heater-magnet module, on Czochralski crystal growth , International scientific colloquium Modeling for electromagnetic processing (MEP 2008), Hannover, Germany, 26/10/2008.
-
F. Tröltzsch: On the optimal control of some heating processes, 60th birthday of J. Sprekels, Berlin, Germany, 22/10/2008.
-
I. Yousept: On a state-constrained optimal control problem involving nonlocal radiation interface conditions, DMV, Erlangen, Germany 16/09/2008.
-
I. Yousept: On a state-constrained optimal control problem involving nonlocal radiation interface conditions, SIAM conference on Optimization, Boston, USA, 11/05/2008.
-
P-E. Druet: Weak solutions to a model for crystal growth from the melt in changing magnetic fields, Conference Optimal Control of Coupled Systems of PDE, Oberwolfach, Germany, 04/03/2008.
-
P-E. Druet: On weak solutions to the system of MHD coupled to heat transfer including nonlocal radiation boundary conditions, Oberseminar analysis, TU Dresden, Germany, 31/01/2008.
-
O. Klein: Modeling Czochralski crystal growth under the influence of electromagnetic forces, Workshop ''Recent advances in free boundary problems and related topics'' (FBP 2006), Levico, Italy, 15/09/2006.
Poster Presentations
-
O. Klein (joined work with Ch. Lechner, P-E. Druet, P. Philip, J. Sprekels, Ch. Frank-Rotsch, F. M Kießling, W. Miller, U. Rehse and P. Rudolph): Numerical simulation of Czochralski crystal growth under the influence of a traveling magnetic field generated by an internal heater-magnet module (HMM), 15th International Conference on Crystal Growth (ICCG15), Salt Lake City, USA, 12-17/08/2007.
-
O. Klein (joined work with W.Dreyer, P-E. Druet, Ch. Lechner and J. Sprekels): Numerical simulation of VCz growth with a traveling magnetic field, 5th International Workshop on Modeling in Crystal Growth (IWMCG-5), Bamberg, Germany, 10-13/09/2006.
Send feedback concerning this page to
Pierre-Étienne Druet.
Last updates:
Pierre-Étienne Druet.
on February 17, 2012,
Olaf Klein
on February 27, 2012,

