An enumerative formula for the spherical cap discrepancy

Holger Heitsch & René Henrion

The spherical cap discrepancy is a widely used measure for how uniformly a sample of points on the sphere is distributed. Being hard to compute, this discrepancy measure is typically replaced by some lower or upper estimates when designing optimal sampling schemes for the uniform distribution on the sphere. We provide a fully explicit enumerative formula for the spherical cap discrepancy. Not surprisingly, this formula is of combinatorial nature and, thus, its application is limited to spheres of small dimension and moderate sample sizes. Nonetheless, it may serve as a useful calibrating tool for testing the efficiency of sampling schemes and its explicit character might be useful also to establish necessary optimality conditions when minimizing the discrepancy with respect to a sample of given size.

 

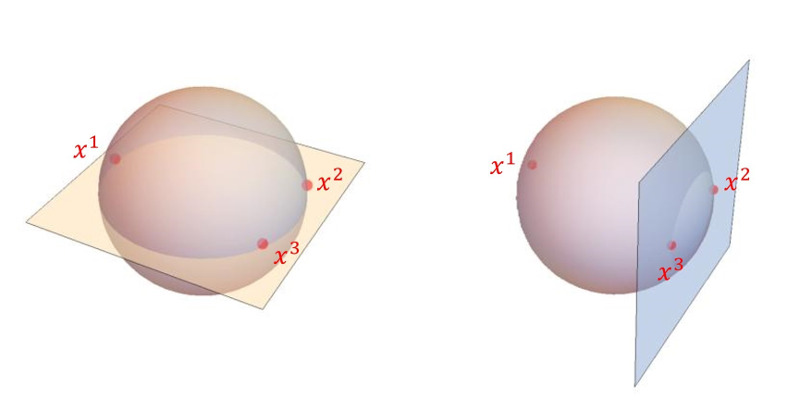
Example of spherical caps on the sphere in the Euclidian space

Matlab code

We provide a free accessible pure academical code of the enumeration formula written in Matlab language. Using the code for any commercial issue requires an explicit permission by the authors. By using the download link you accept the licensing agreement below.

Main function: cdiscr.m
Required subroutines: cap_measure.m, emp_measure.m
Example script: example.m

Licensing agreement: The code is free of charge but for academic purpose only. The code is provided with absolutely no warranty.

Reference

H. Heitsch and R. Henrion: An enumerative formula for the spherical cap discrepancy, Journal of Computational and Applied Mathematics 390 (2021), appeared online.