Publication on Large-scale stochastic simulation of open quantum systems in Nature Communications
A research team from Technische Universität München, Freie Universität Berlin, Helmholtz-Zentrum Berlin, Zuse Institute Berlin, and the Weierstrass Institute successfully publisehd a paper on Large-scale stochastic simulation of open quantum systems in Nature Communications.
Open quantum systems are essential for realistic physical models and robust quantum technologies, but they are numerically notoriously hard to simulate, because the parameters of the dynamics generated by the Lindblad master equation grow exponentially in system size.
In this work, we introduce the Tensor Jump Method (TJM) as an embarrassingly parallel stochastic approach that transfers the MCWF/quantum-trajectory ideas to a highly efficient matrix product states (MPS) algorithm. It combines dynamic TDVP time-evolution on rank adaptive tensor manifolds, with Strang-splitting of the effective non-Hermitian Hamiltonian and a sampling MPS strategy to drastically reduce the dimensionality of the simulation problem.
We warmly thank all collaborators for this highly productive joint effort (Jens Eisert (FU Berlin / HZB), Patrick Gelss (Zuse Institute Berlin), Richard Milbradt, Robert Wille (TU Munich), Christian Mendl (TU Munich)), and in particular Aaron Sander (TU Munich) for initiating and driving the project and for enabling our close involvement throughout.
WIAS researchers Maximilian Fröhlich, Martin Eigel, and Michael Hintermüller contributed the convergence results and error analysis as the basis for reliable simulations, the dissipative contraction and rank-adaptive manifold evolution for flexible and efficient entanglement representation and the complexity analysis.
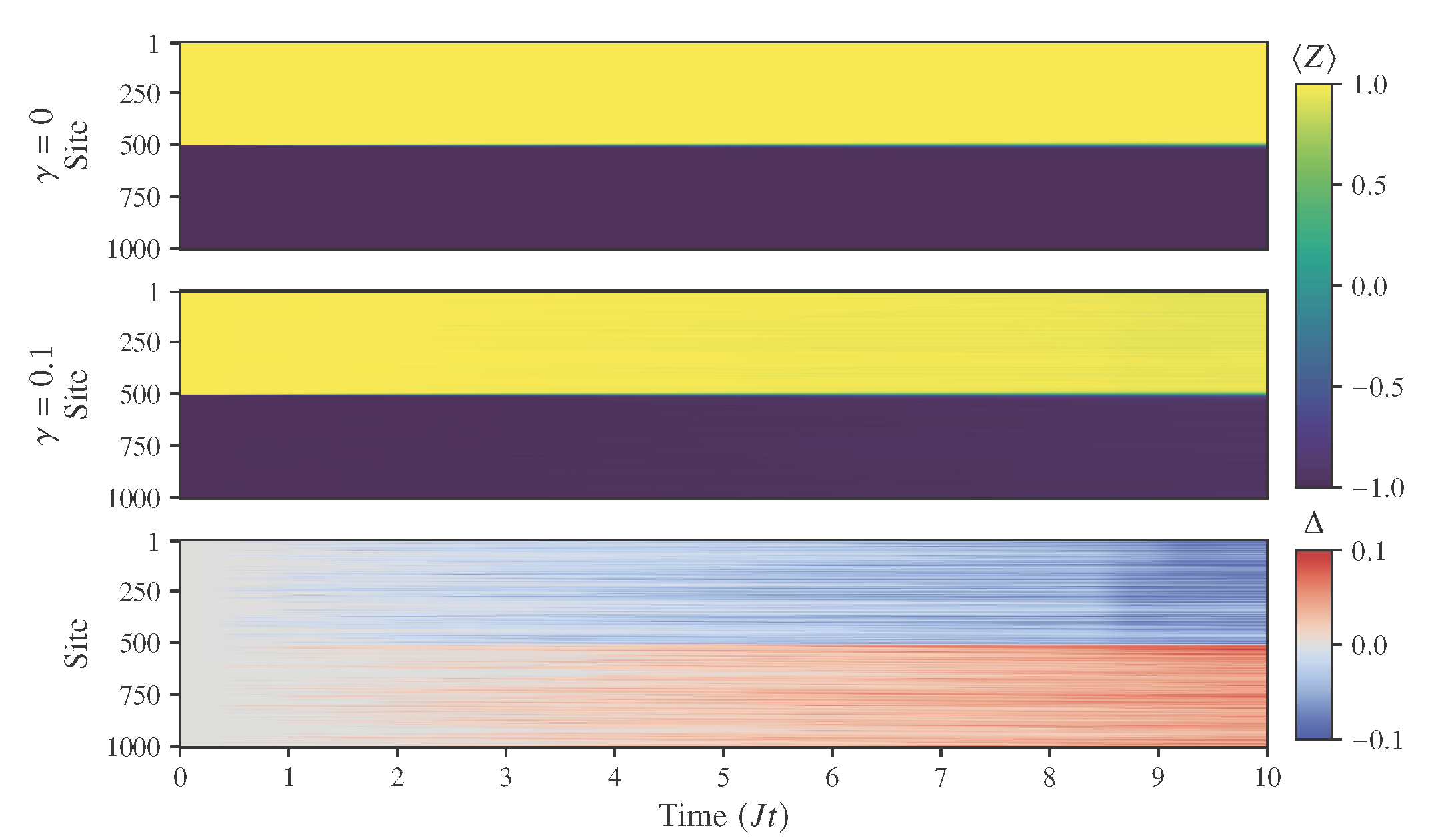
As a particular highlight, scalability up to 1.000 spins of a noisy XXX Heisenberg chain on consumer-grade hardware is demonstrated, opening the door to studying dissipative many-body dynamics at sizes that were previously practically out of reach.