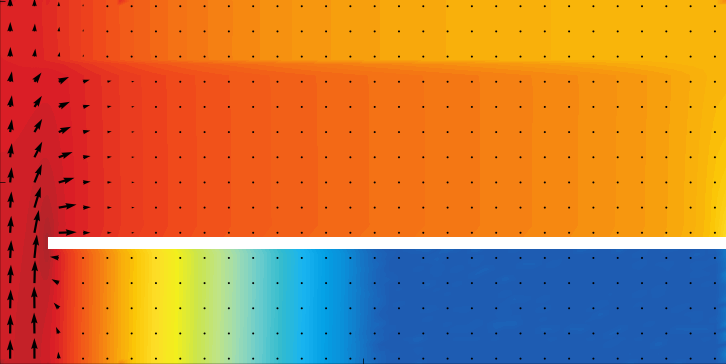
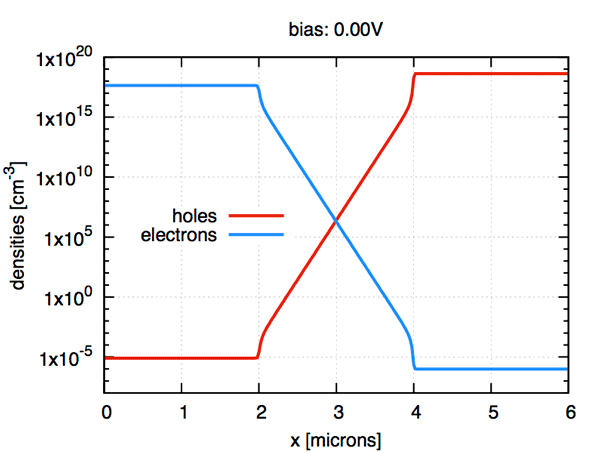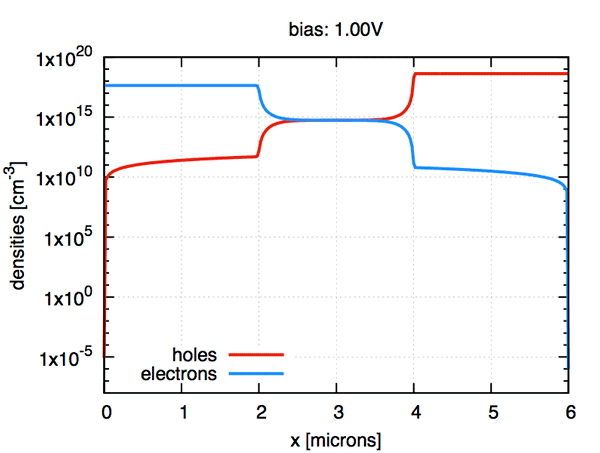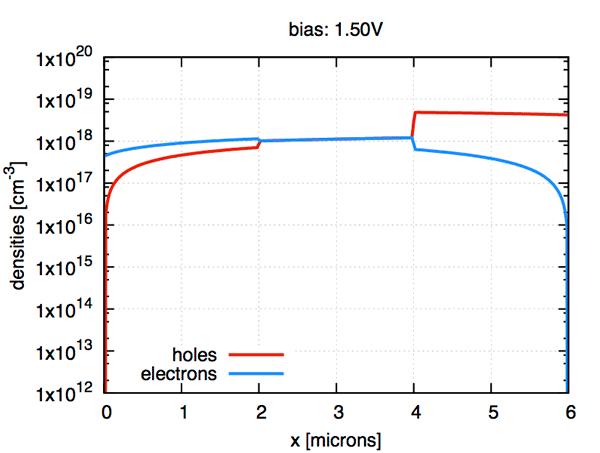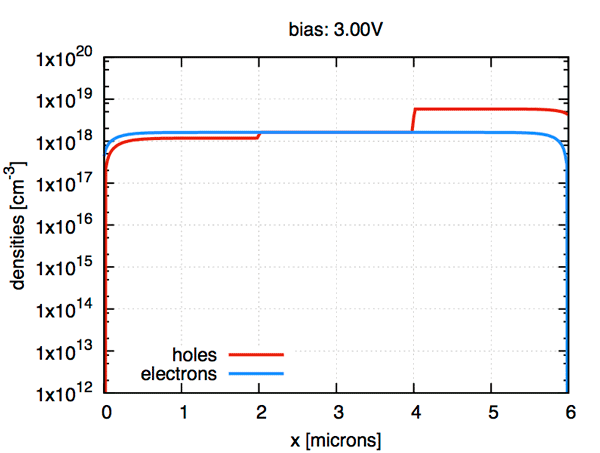
ddfermi is an open-source software prototype which simulates drift diffusion processes in classical and organic semiconductors.

Key features

  • finite volume discretization of the semiconductor equations (van Roosbroeck system)
  • thermodynamically consistent Scharfetter-Gummel flux discretizations
  • general statistics: Fermi-Dirac, Gauss-Fermi, Blakemore and Boltzmann
  • multidimensional devices
  • based on pdelib and interfaced via Python or Lua

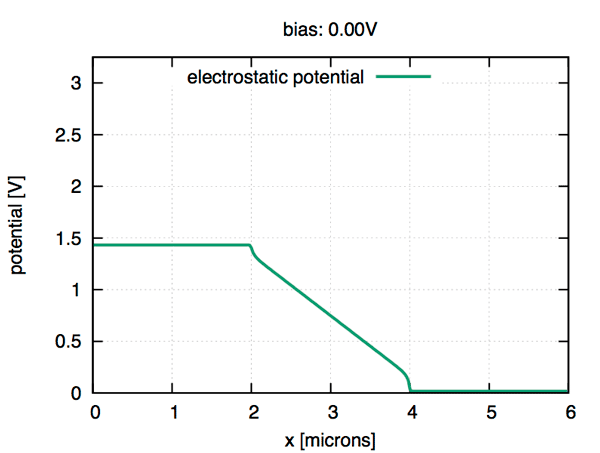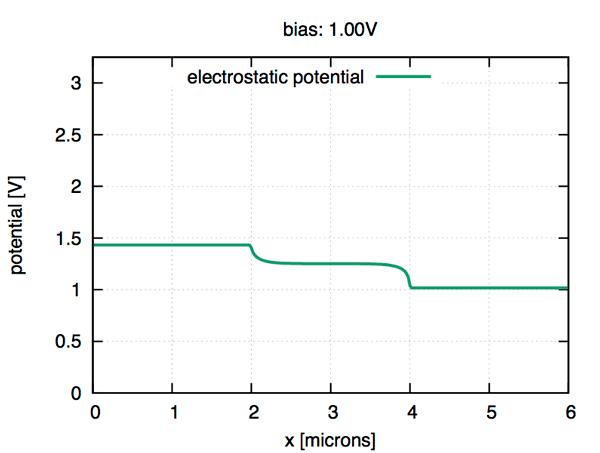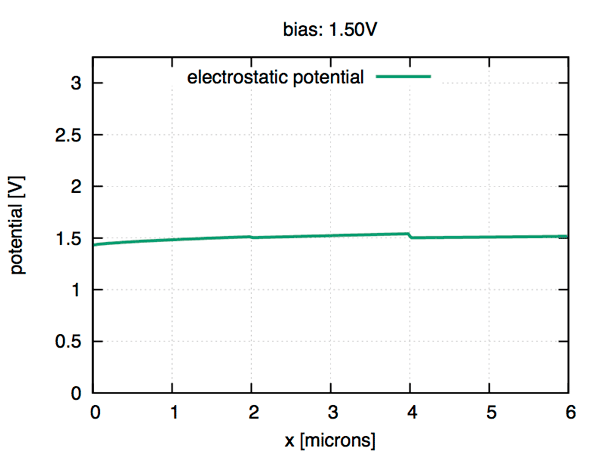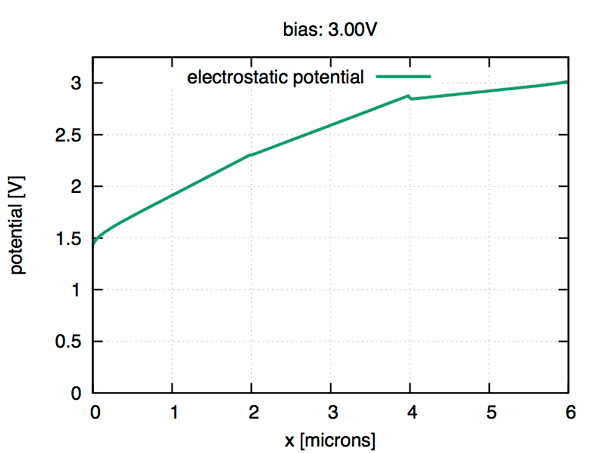
Developers


DOI for Citations and BibTex

http://doi.org/10.20347/WIAS.SOFTWARE.DDFERMI (also accessible via http://doi.org/10.20347/WIAS.SOFTWARE.14)

@article{ddfermi,
author = "Doan, D. H. and Farrell, P. and Fuhrmann, J. and Kantner, M. and Koprucki, T. and Rotundo, N.",
year = 2016,
title = "ddfermi -- a drift-diffusion simulation tool",
doi = {10.20347/WIAS.SOFTWARE.DDFERMI},
type = "Version 0.1.0",
institution = "Weierstrass Institute (WIAS)"
url = {http://doi.org/10.20347/WIAS.SOFTWARE.DDFERMI} }

Publications using ddfermi

  1. T. Koprucki, N. Rotundo, P. Farrell, H. Doan, J. Fuhrmann. On Thermodynamic Consistency of a Scharfetter-Gummel Scheme Based on a Modified Thermal Voltage for Drift-Diffusion Equations with Diffusion Enhancement, Optical and Quantum Electronics, 47-6 (2015), pp. 1327-1332, preprint, doi
  2. P. Farrell, J. Fuhrmann, T. Koprucki. Computational and Analytical Comparison of Flux Discretizations for the Semiconductor Device Equations beyond Boltzmann Statistics, Journal of Computational Physics 346 (2017), pp. 497-513, preprint, doi
  3. P. Farrell, N. Rotundo, H. Doan, M. Kantner, J. Fuhrmann, T. Koprucki. Drift-Diffusion Models, book chapter, Handbook of Optoelectronic Device Modeling and Simulation, J. Piprek (ed), Taylor & Francis, (2017), preprint, doi
  4. M. Patriarca, P. Farrell, J. Fuhrmann, T. Koprucki. Highly Accurate Quadrature-based Scharfetter-Gummel Schemes for Charge Transport in Degenerate Semiconductors, Computer Physics Communications 235 (2018), pp. 40-49, preprint, doi
  5. F. Sawatzki, D. Doan, H. Kleemann, M. Liero, A. Glitzky, T. Koprucki, K. Leo. Balance of Horizontal and Vertical Charge Transport in Organic Field-Effect Transistors, Physical Review Applied 10 (2018), pp. 034069, doi
  6. S. Kayser, P. Farrell and N. Rotundo. Detecting striations via the lateral photovoltage scanning method without screening effect. Optical and Quantum Electronics 53, (2021): 288, doi
  7. S. Kayser, N. Rotundo, N. Dropka, and P. Farrell. Assessing doping inhomogeneities in GaAs crystal via simulations of lateral photovoltage scanning method. Journal of Crystal Growth 571 (2021): 126248, doi
  8. M. O'Donovan, P. Farrell, T. Streckenbach, T. Koprucki and S. Schulz. Multiscale simulations of uni-polar hole transport in (In, Ga) N quantum well systems. Optical and Quantum Electronics 54 (2022), doi
  9. R. Finn, M. O'Donovan, P. Farrell, J. Moatti, T. Streckenbach, T. Koprucki, S. Schulz. Theoretical study of the impact of alloy disorder on carrier transport and recombination processes in deep UV (Al, Ga) N light emitters. Applied Physics Letters, 122 24 (2023), doi
  10. M. O'Donovan, P. Farrell, J. Moatti, T. Streckenbach, T. Koprucki, S. Schulz. Impact of random alloy fluctuations on the carrier distribution in multicolor (In,Ga)N/GaN quantum well systems. Phys. Rev. Applied, 21 024052 (2024), doi

Related publications

  1. M. Bessemoulin-Chatard. A finite volume scheme for convection-diffusion equations with nonlinear diffusion derived from the Scharfetter-Gummel scheme, Numerische Mathematik 121 (2012), pp. 637-670, doi
  2. J. Fuhrmann. Comparison and numerical treatment of generalised Nernst-Planck models, Computer Physics Communications 196 (2015), pp. 166-178, preprint, doi
  3. K. Gärtner. Existence of bounded discrete steady state solutions of the van Roosbroeck system with monotone Fermi-Dirac statistic functions, Journal of Computational Electronics 3 (2015), pp. 773-787, preprint, doi
  4. T. Koprucki, K. Gärtner. Discretization scheme for drift-diffusion equations with strong diffusion enhancement, Optical and Quantum Electronics 45 (2013), pp. 791-796, preprint, doi
  5. D. Scharfetter, H. Gummel. Large-signal analysis of a silicon Read diode oscillator, IEEE Transactions on Electron Devices 16 (1969), pp. 64-77

Contact

Phone, E-mail

Tel.: 030 20372-560
E-mail: ddfermi@wias-berlin.de


WIAS Software