We offer a course introducing the theoretical background of mesh
generation and the state-of-the-art methods and softwares for
generating meshes for scientific computing. The aim of this course is
to give the audience an introduction to the research and development
in the field of mesh and grid generation. The audience will also learn
to use some freely available meshing softwares which are based on the
introduced methods. This will allow the audience to develop advanced
methods or properly choose the right methods and tools in solving
challenging engineering problems in scientific computing.
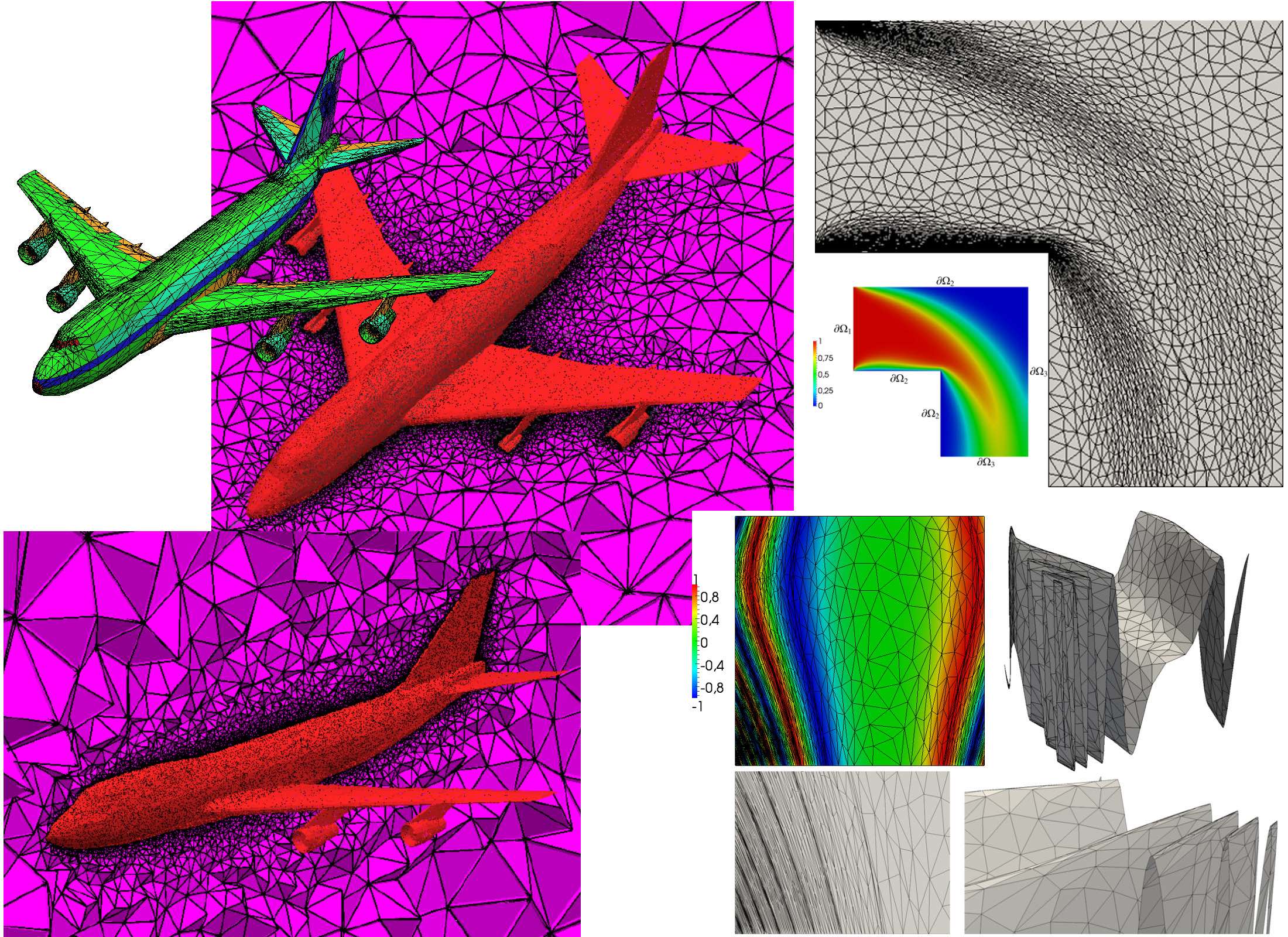
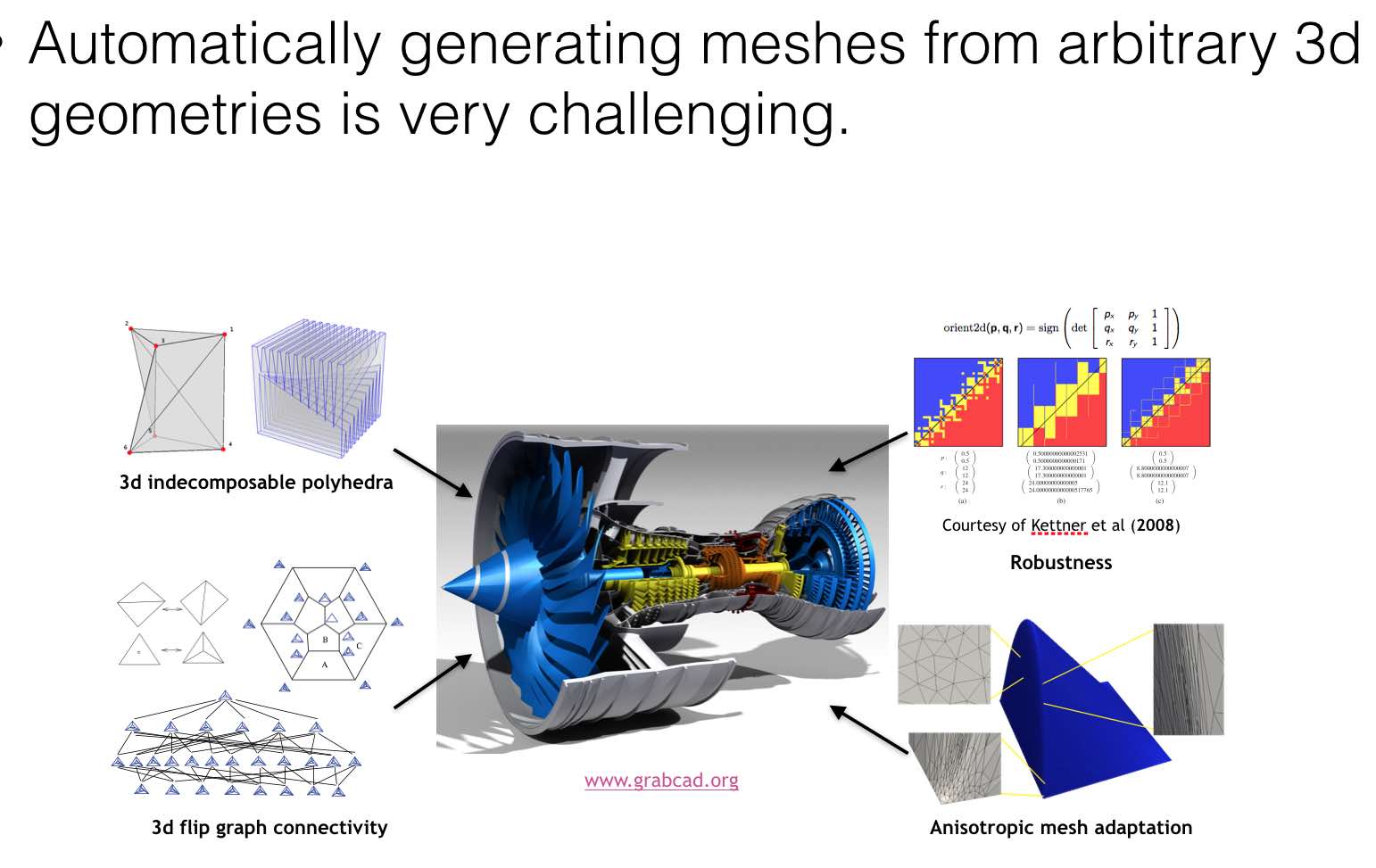
A main theme of this course is on the theory and algorithms of
generating unstructured meshes, such as like triangular and
tetrahedral meshes. They are well suited for complicated geometries,
can be generated fully automatically, and are feasible for locally
mesh adaption. Emphases are given on those methods which have solid
theoretical background and good heuristics.
Robust and efficient techniques for implementations are introduced.
| Date
| Time
| Topics
| Lecture Materials
| Home Work
|
| July 1
| 08:00 -- 11:30
| Introduction
| Lecture 1
|
|
|
|
| What is mesh generation?
about this course,
incremental construction,
the convex hull problem
| Fundamentals.pdf
|
|
|
|
| Triangulations in the plane
|
|
|
|
|
| Defnitions, simplicial complexes,
planar graphs, Euler's formula,
a sweepline algorithm
|
|
|
|
|
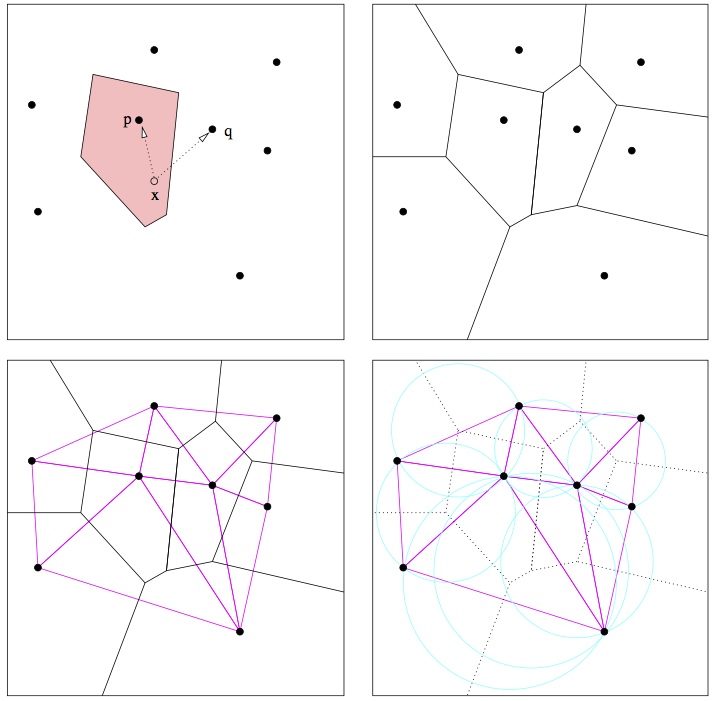
| Delaunay triangulations
|
|
|
|
|
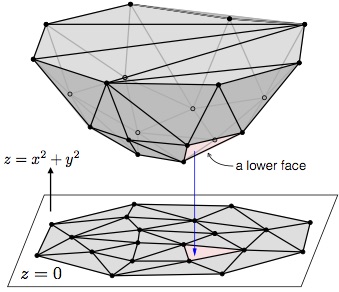
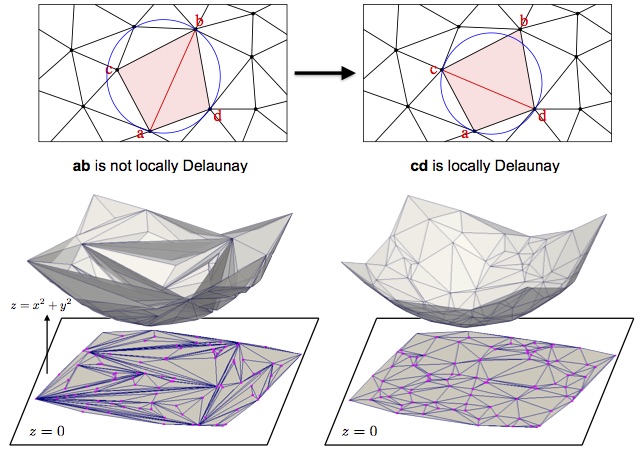
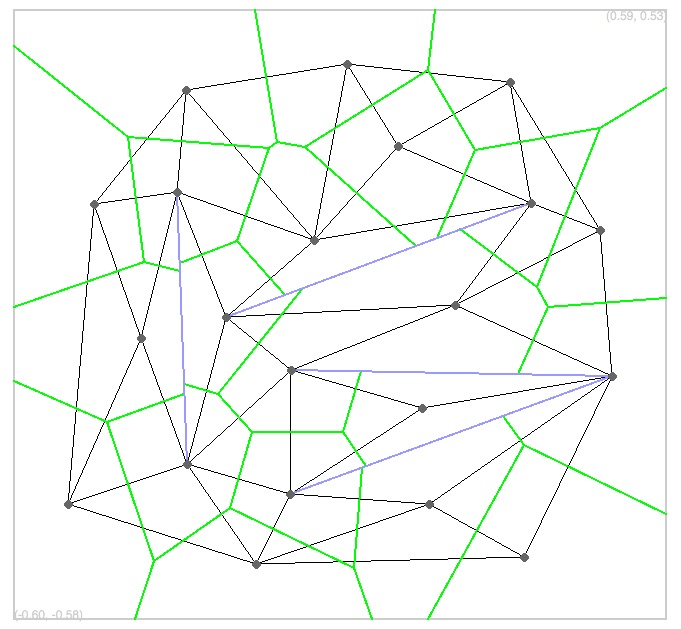
| Voronoi diagrams, empty circumcircle criterion
lifting transformation, the Delaunay lemma,
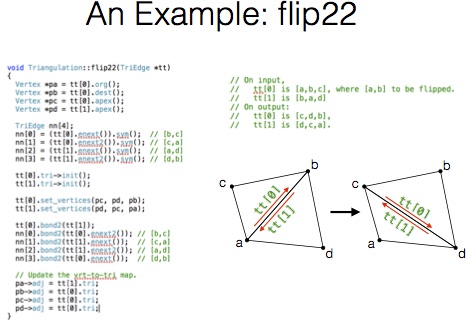
Lawson's flip algorithm
randomized incremental flip algorithm
|
|
|
|
|
| Software implementation
|
|
|
|
|
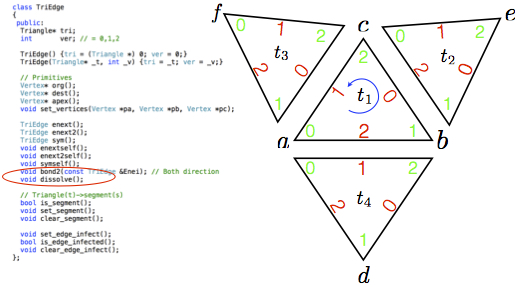
| Triangle-based data structure, point location
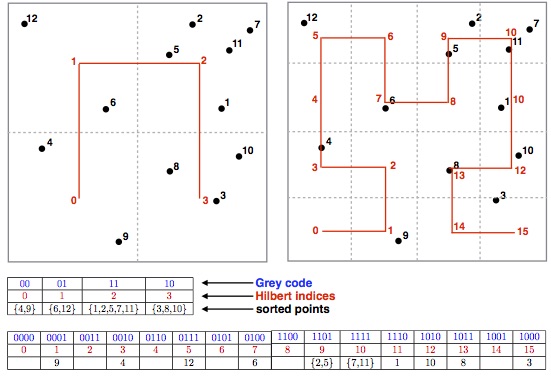
spatial sorting, hilbert curve sorting
exact filtered predicates
|
|
|
|
|
| Triangular Mesh Generation and Adaptation
|
|
|
|
|
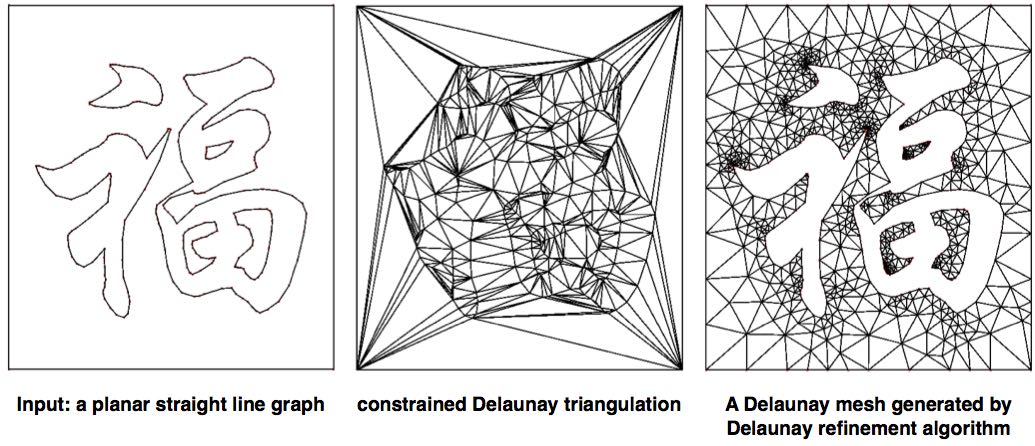
| Constrained Delaunay triangulation,
quality mesh generation, Delaunay refinement,
mesh adaptation,
optimal Delaunay triangulation,
centroidal Voronoi tessellation
|
|
|
|
|
| Weighted Delaunay triangulations
|
|
|
|
|
| Weighted points, weighted distance
Power diagram, orthogonality,
duality, regular subdivisons, Acyclic theorem
incremental flip construction
|
|
|
|
|
| Tetrahedral mesh generation and Adaptation
|
|
|
|
|
| The Schoenhardt polyhedron, Steiner points
Constrained Delaunay tetrahedralisations,
Shewchuk's CDT theorem, incremental CDT algorithm
Delaunay refinement, sharp features
mesh adaptation
|
|
|
|
|
| Review and further topics
|
|
|
|
|
|
|
|
|