Head:N.N.
Partners are:
The WIAS researchers of the research network form the Leibniz group 1.
Modeling of coupled flow processes is an urgent and largely unsolved interdisciplinary problem. They have eminent importance in energy research, geosciences, environmental and climate research, civil engineering and materials science.
Common topics of the network:
Mathematical models:
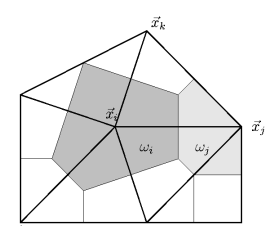 The discretization of species transport and reaction phenomena in coupled flow processes is a challenging and urgent problem, since they arise in many applications like energy research, and environmental sciences. Species transport and reaction phenomena are modeled by systems of coupled reaction-convection-diffusion equations. Their discretization with classical vertex-based finite volume methods on boundary-conforming Delaunay grids leads to discrete nonlinear equations with similar qualitative properties as the original continuous equations, e.g.,
The discretization of species transport and reaction phenomena in coupled flow processes is a challenging and urgent problem, since they arise in many applications like energy research, and environmental sciences. Species transport and reaction phenomena are modeled by systems of coupled reaction-convection-diffusion equations. Their discretization with classical vertex-based finite volume methods on boundary-conforming Delaunay grids leads to discrete nonlinear equations with similar qualitative properties as the original continuous equations, e.g.,
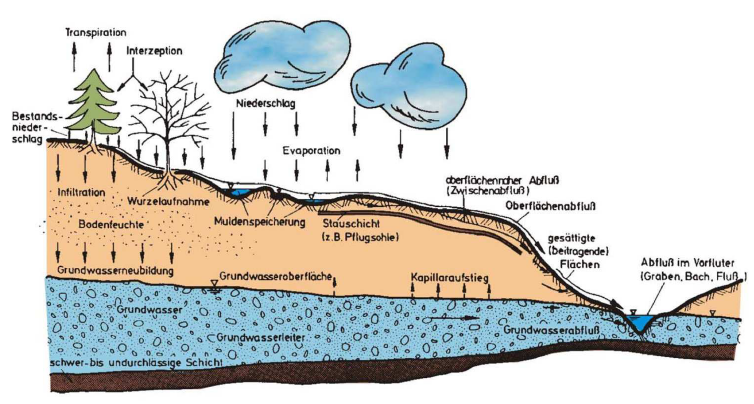
Additional challenges for an appropriate modeling of coupled flow processes arise, when porous media flows and flows obeying the Stokes and Navier-Stokes equations occur together in different parts of the underlying domain. Then, appropriate boundary conditions for the transition interface between the porous medium and the free flow region have to be used, e.g., the Beavers-Joseph condition.
This group existed from 2008 to 2010. It was led by Juergen Fuhrmann.
The research network "Coupled Flow Processes in Energy and Environmental Research" has been established in January 2008 as the result of a successful joint proposal in the framework of the competitive procedure of the Leibniz Association within the "Joint Initiative for Research and Innovation" launched in 2005 by the German Federal Ministry for Education and Research.Partners are:
- Weierstrass Institute for Applied Analysis and Stochastics, Head (and co-ordinator of the network): Dr. Jürgen Fuhrmann
- Potsdam Institute for Climate Impact Research, Head: Dr. Uwe Böhm
- Freie Universität Berlin, Heads: Prof. Dr. Rupert Klein & Prof. Dr. Ralf Kornhuber
- Friedrich-Alexander-Universität Erlangen-Nürnberg, Head: Prof. Dr. Eberhard Bänsch
The WIAS researchers of the research network form the Leibniz group 1.
Modeling of coupled flow processes is an urgent and largely unsolved interdisciplinary problem. They have eminent importance in energy research, geosciences, environmental and climate research, civil engineering and materials science.
Common topics of the network:
- reactive transport of dissolved species
- interaction between free flow and flow in porous media
- exchange processes in multi-phase flows
 |  |
Mathematical models:
- free flow: (incompressible) Navier-Stokes equations
- porous media flow: Darcy and Brinkman model
- soil hydrology: (stochastic) Richards equation
- species transport: reaction-diffusion-convection equation
- interface conditions: boundary layer theory, Beavers-Joseph, ...
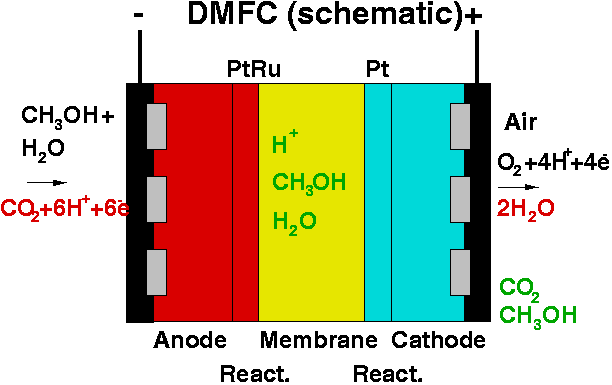
- flow and transport processes in fuel cells
- estimation of the impact of near-surface hydrological processes on the regional climate
Leibniz group 1
The focus of the Leibniz group 1 is on:- Numerical analysis: Discretization schemes for the Navier-Stokes equation on unstructured grids which preserve qualititive mathematical properties of the continuous model
- Modelling: interface conditions between free flow and porous media flow

- a local maximum principle and
- positivity.
- using appropriate projections of classical flow discretizations like, e.g., FE methods or
- an appropriate direct discretization of the flow equations by edge-based finite volume methods.
 |  |
Additional challenges for an appropriate modeling of coupled flow processes arise, when porous media flows and flows obeying the Stokes and Navier-Stokes equations occur together in different parts of the underlying domain. Then, appropriate boundary conditions for the transition interface between the porous medium and the free flow region have to be used, e.g., the Beavers-Joseph condition.
Aims
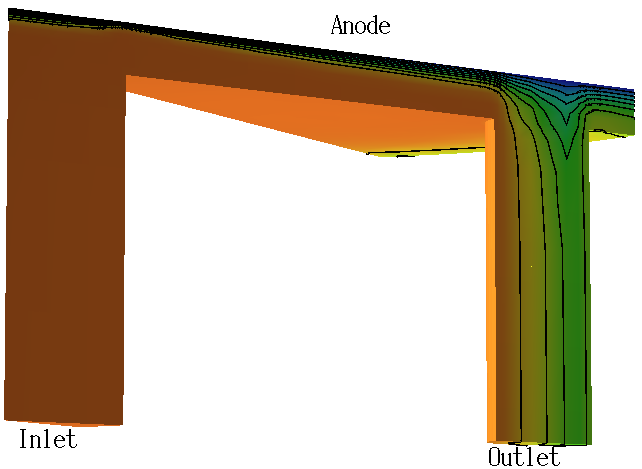
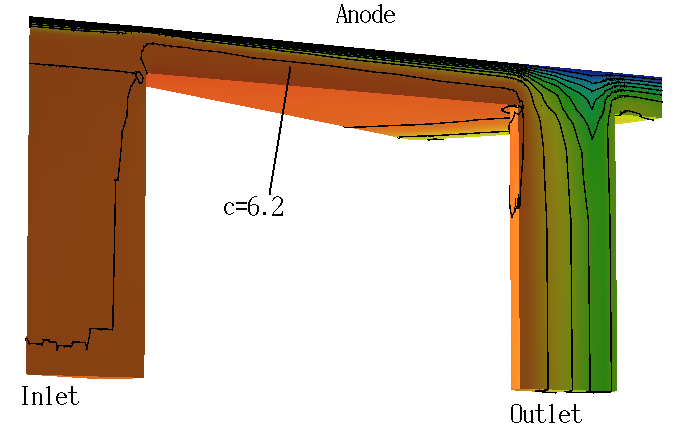
Simulation of flow cell experiments in electrochemistry:
The Darcy and Navier-Stokes equations are coupled with a convection-diffuson equation for the species transport by the convective flux.
Electro-convective instability and electro-dialysis:
The Nernst-Planck-Poisson equations are coupled with the Stokes or Navier-Stokes equations by the convective flux and by the momentum transfer from the moving ions onto the fluid particles.