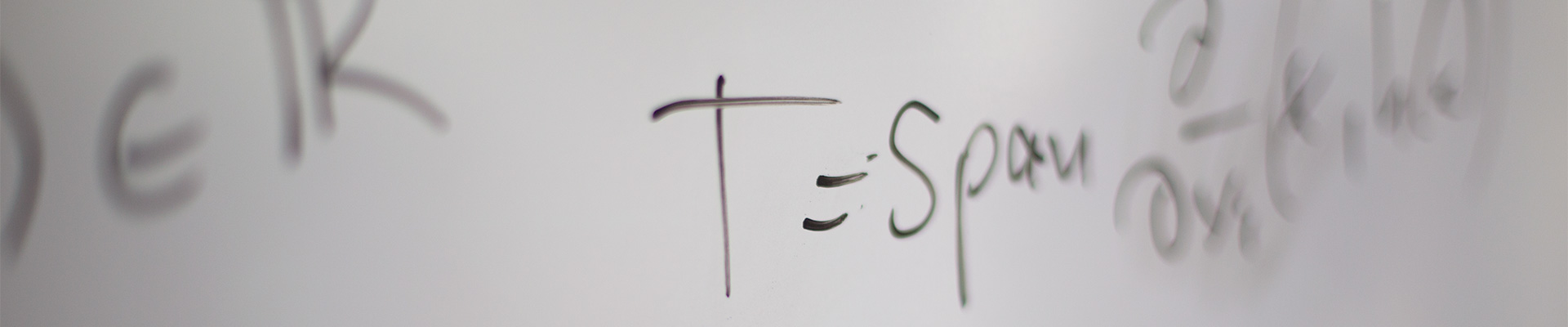A rigorous numerical method for the optimal design of binary gratings
Authors
- Elschner, Johannes
- Schmidt, Gunther
2010 Mathematics Subject Classification
- 78-05 78A45 35J20 65N30 49J20
Keywords
- Diffraction problems, Helmholtz equation, transmission problem, strongly elliptic variational formulation, generalized FEM, gradient methods
DOI
Abstract
In this paper we describe recent developments in the application of mathematical and computational techniques to the problem of designing binary gratings on top of a multilayer stack in such a way that the propagating modes have a specified intensity or phase pattern for a chosen range of wavelengths or incidence angles. This optimal design problem is solved by a minimization algorithm based on gradient descent, the exact calculation of gradients of certain functionals with respect to the parameters of the grating profile and the thickness of the layers. For the computation of diffraction efficiencies and of the gradients we use a reliable finite element method which originates from variational formulations of the diffraction problems. We provide several numerical examples including polarisation gratings and beam splitters to demonstrate the efficiency of the algorithm.
Appeared in
- J. Comput. Physics 146 (1998), pp. 603-626
Download Documents