Project: Modeling and analysis of suspension flows (AA2-4)
MATH+ Application Area: Materials, Light, Devices
Acknowledgement: This research is carried out in the framework of the DFG funded
Cluster of Excellence EXC 2046
MATH+: The Berlin Mathematics Research Center
within the Application Area Materials, Light and Devices.
The funding period of the project is from January 2019 until December 2020.
Background and goals
|
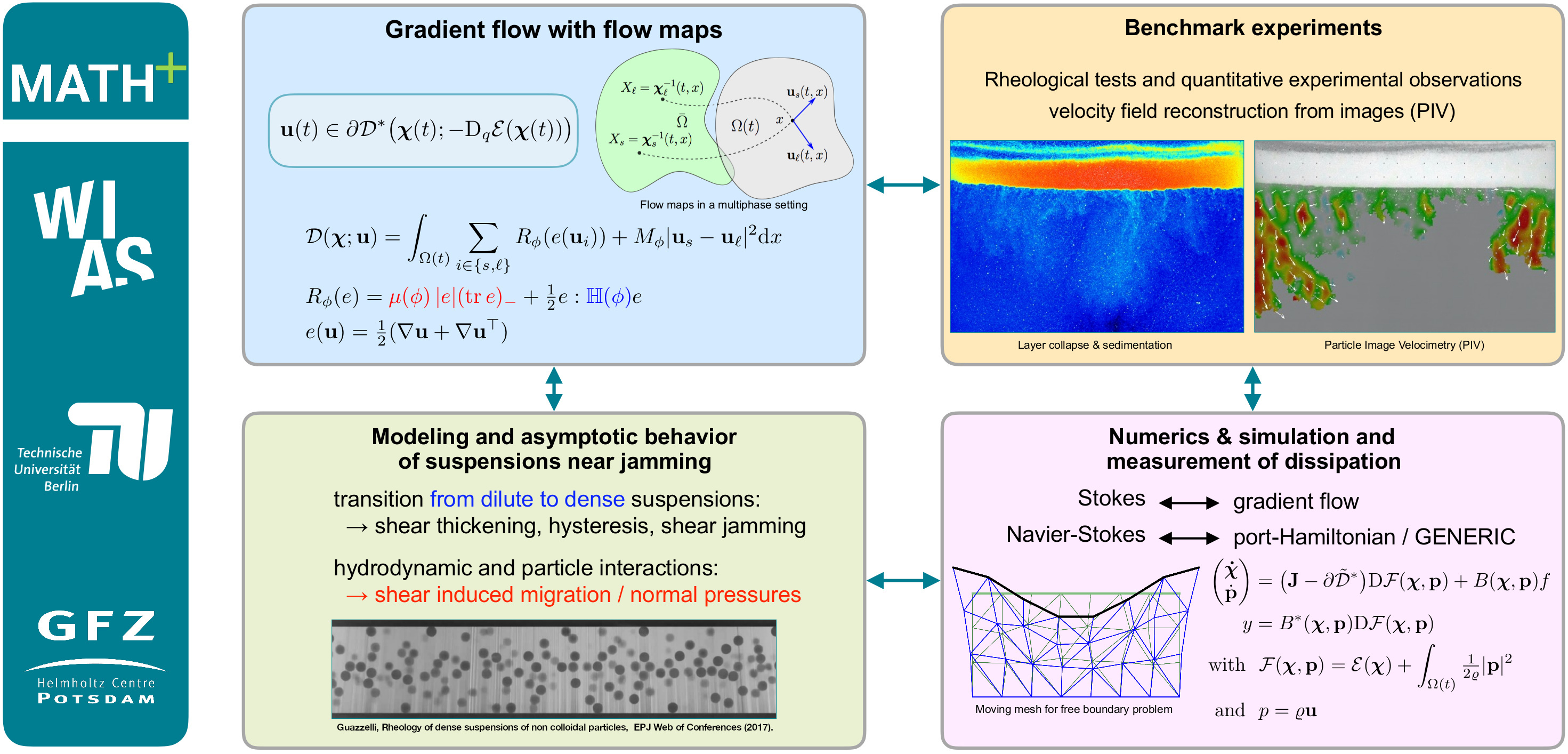
The goal of the MATH+ project AA2-4 Modeling and analysis of suspension flows is to derive a unified continuum model applicable from dilute to dense, jammed suspensions.
Their mathematical description
provides an ongoing challenge since suspensions show much different behavior in different concentration regimes: While dilute suspensions, i.e., mixtures with low volume fraction and large
particle distances, have small or negligible interparticle interaction, concentrated or dense suspensions have strong interactions that lead to constitutive material laws not present in standard fluids: Here, interparticle interactions generate a normal pressure, which is a major driving force
for shear induced particle migration.
While the effective material laws for
dilute suspensions are satisfactorily captured by the thesis of Albert Einstein, these laws clearly
fail for the transition to the dense or jammed regime. For the prediction of suspension behavior
in applications it would be a major success to establish a single model that captures all these
different effects and thus allows for the transition between the different regimes.
It is a joint project with the Technische Universität Berlin (V. Mehrmann) and the Weierstrass Institute (D. Peschka, M. Thomas, B. Wagner), that also involves the close collaboration with the German Research Centre for Geosciences, GFZ (M. Rosenau).
|
|
The mathematical model, i.e., the partial differential equation (PDE) in the preliminary work [5], is constructed using a generalized gradient flow approach based on an energy generating forces and a non-smooth convex dissipation functional which generates the PDE dynamics from these forces.
In this way, we deduce one possible model to describe flows of two-phase mixtures with free, evolving boundaries and we provide the underlying construction for gravity-driven and surface-tension driven flows, see [5].
It is the goal of this project to extend this model by conservative effects thus leading to a port-Hamiltonian or GENERIC system in the spirit of [4] and to investigate the resulting system analytically and numerically.
Mathematical challenges of such a two-phase mixture flow model are:
- the presence of additional non-smooth terms in the viscous stress tensor,
- a-priori unknown domains with moving boundaries, and
- regions of vaccum/degeneracy.
The resulting model will be compared and adjusted to suitably tailored experiments carried out by M. Rosenau at the GFZ Potsdam.
|

|
|
Project related events
- Workshop: PDE 2019: "Partial Differential Equations in Fluids and Solids", Weierstrass Institute Berlin, 9-13 September 2019.
- Minisymposium: ``Recent advances in understanding suspensions and granular media flow'' organized by A. Münch (Oxford) and D. Peschka at 9th International Congress on Industrial and Applied Mathematics (ICIAM 2019) in Valencia, July 15-19, 2019.
- Upcoming Thematic Einstein Semester WS2020/21: ``Energy-based mathematical methods for reactive multiphase flows'' organized by M. Thomas, B. Wagner, A. Mielke, V. Mehrmann, D. Peschka
|
Guests
- Prof. Luca Heltai (long term), SISSA, Trieste, May 29-July 31, 2019.
- Prof. Uwe Thiele (jointly with RG7, talk Material Modeling Seminar), Münster, February 27-28, 2019.
|
Publications and preliminary work
| [6] |
M.H. Farshbaf-Shaker, M. Thomas, Analysis of a compressible Stokes-flow with degenerating and singular viscosity, pdf file, 2020.
|
| [6] |
D. Peschka, M. Rosenau, Two-phase flows for sedimentation of suspensions, WIAS Preprint 2743, 2020.
|
| [5] |
D. Peschka, M. Thomas, T. Ahnert, A. Münch, and B. Wagner, Gradient structures for flows of concentrated suspensions, Springer-CIM Series, 2019.
|
| [4] |
A. M. Badlyan, B. Maschke, C. Beattie, and V. Mehrmann, Open physical systems: from GENERIC to
port-Hamiltonian systems, MTNS Hong Kong, 2018.
|
| [3] |
T. Ahnert, A. Münch, B. Niethammer, and B. Wagner, Stability of concentrated suspensions under Couette
and Poiseuille flow, J. Eng. Math., 2018.
|
| [2] |
T. Ahnert, A. Münch, and B. Wagner, Models for the two-phase
flow of concentrated suspensions, Eur. J. Appl. Math., 2018.
|
| [1] |
M.C. Ritter, T. Santimano, M. Rosenau, K. Leever, and O. Oncken, Sandbox rheometry: Co-evolution of
stress and strain in riedel-and critical wedge-experiments, Tectonophysics, 2018.
|
|
Talks and posters
- Poster: M.H. Farshbaf Shaker, D. Peschka, M. Thomas, Modeling and analysis of syspension flows, Visit of the scientific advisory board of MATH+, November 11, and MATH+ Day, December 13, 2019.
- Invited Talk: M. Thomas, GENERIC structures with bulk-interface interaction, SFB 910 Symposium "Energy based modeling, simulation and control", TU Berlin, October 25, 2019.
- Invited Talk: M. Thomas, "Gradient structures for flows of concentrated suspensions", Thematic Minisymposium MS ME-0-75 "Recent advances in understanding suspensions and granular media flow", ""9th International Congress on Industrial and Applied Mathematics" (ICIAM 2019, Valencia), July 15-19, 2019.
- Invited Talk: D. Peschka, Dynamic contact angles via generalized gradient flows, Modelling of Thin Liquid Films - Asymptotic Approach vs. Gradient Dynamics, Banff International Research Station, Banff, Canada, April 30, 2019.
- Invited Talk: D. Peschka, Gradient formulations with flow maps - mathematical and numerical approaches to free boundary problems, Kolloquium des Graduiertenkollegs 2339, Universität Regensburg, May 24, 2019.
- Talk: D. Peschka, Modeling, simulation, and experiments for flows of concentrated suspensions, Langenbach-Seminar, WIAS Berlin, April 24, 2019.
- Poster: D. Peschka, Dynamic Contact Angles via Gradient Flows, 694. Heraeus seminar on "Wetting on soft or microstructured surfaces", Bad Honnef, Germany, April 11-13, 2019.
- Talk: D. Peschka, Gradient structures for flows of concentrated suspensions - jamming and free boundaries, 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2019), Section S11 ``Interfacial Flows", Technische Universität Wien, Austria, February 20, 2019.
- Invited Talk: D. Peschka, Mathematical modeling of fluid flows using gradient systems, Seminar in PDE and Applications, Delft University of Technology, Netherlands, May 28, 2019.
|



