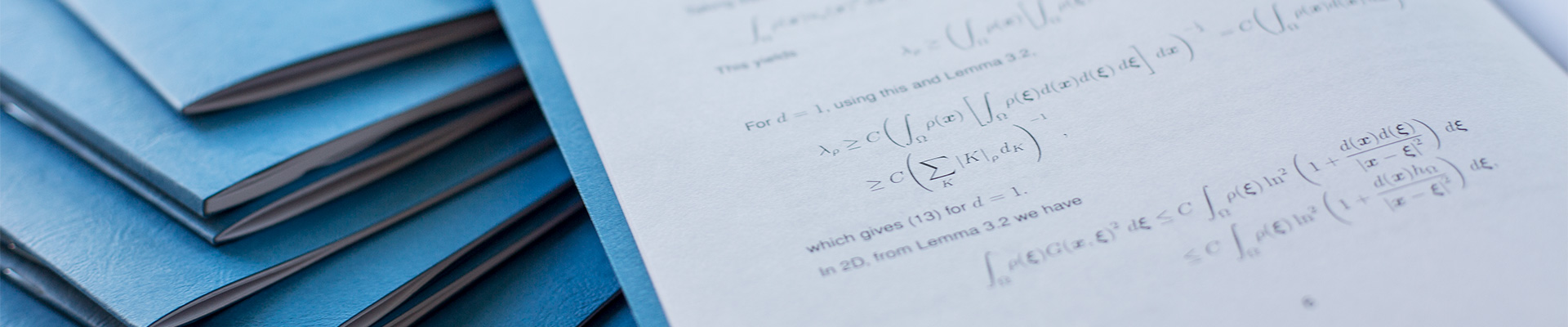Stochastic models in kinetic theory
Authors
- Wagner, Wolfgang
2010 Mathematics Subject Classification
- 60J28 82C40
Keywords
- Kinetic equations, stochastic models, finite number of states, fluctuations
DOI
Abstract
The paper is concerned with some aspects of stochastic modelling in kinetic theory. First, an overview of the role of particle models with random interactions is given. These models are important both in the context of foundations of kinetic theory and for the design of numerical algorithms in various engineering applications. Then, the class of jump processes with a finite number of states is considered. Two types of such processes are studied, where particles change their states either independently of each other (mono-molecular processes), or via binary interactions (bi-molecular processes). The relationship of these processes with corresponding kinetic equations is discussed. Equations are derived both for the average relative numbers of particles in a given state and for the fluctuations of these numbers around their averages. The simplicity of the models makes several aspects of the theory more transparent.
Appeared in
- Phys. Fluids, 23 (2011) pp. 030602: 1--14.
Download Documents