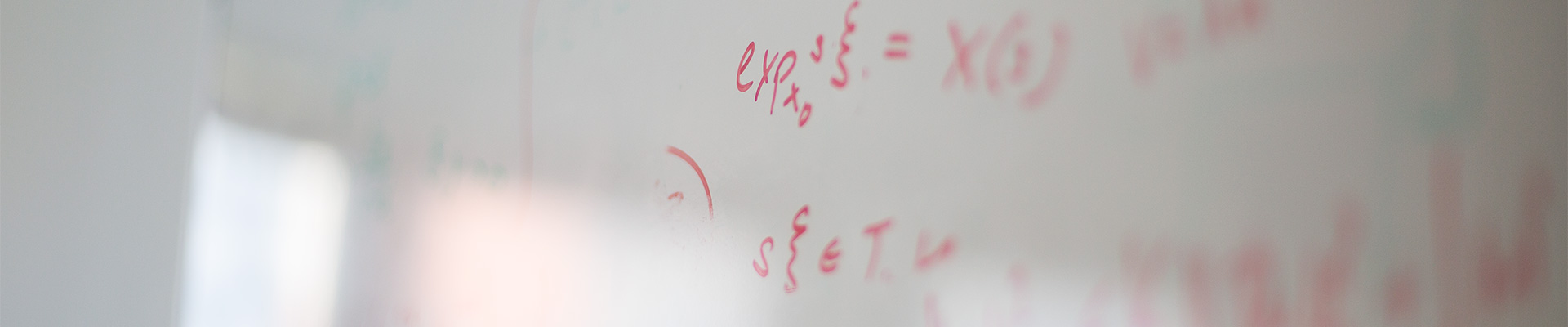Exponential dichotomies for solitary-wave solutions of semilinear elliptic equations on infinite cylinders
Authors
- Peterhof, Daniela
- Sandstede, Björn
- Scheel, Arnd
2010 Mathematics Subject Classification
- 35J65 35B32 35B40
Keywords
- dynamical system treatment of elliptic equations
DOI
Abstract
In applications, solitary-wave solutions of semilinear elliptic equations Δu + g(u,∇u) = 0 (x,y) ∈ ℝ × Ω in infinite cylinders frequently arise as travelling waves of parabolic equations. As such, their bifurcations are an interesting issue. Interpreting elliptic equations on infinite cylinders as dynamical systems in x has proved very useful. Still, there are major obstacles in obtaining, for instance, bifurcation results similar to those for ordinary differential equations. In this article, persistence and continuation of exponential dichotomies for linear elliptic equations is proved. With this technique at hands, Lyapunov-Schmidt reduction near solitary waves can be applied. As an example, existence of shift dynamics near solitary waves is shown if a perturbation µ h(x,u,∇u) periodic in x is added.
Appeared in
- J. Differential Equations, 140 (1997), pp. 266-308
Download Documents