Project: Variational methods for viscoelastic flows and gelation (AA2-9)
MATH+ Application Area: Materials, Light, Devices
Acknowledgement: This research is carried out in the framework of the DFG funded
Cluster of Excellence EXC 2046
MATH+: The Berlin Mathematics Research Center
within the Application Area Materials, Light and Devices.
The funding period of the project is from January 2021 until December 2022.
Summary
|
We study continuum formulations for flows of elastic particles immersed in a liquid and their gelation by variational modeling, mathematical analysis, and structure-preserving discretizations. The resulting models will be calibrated using experimental data.
|
|
Description
|
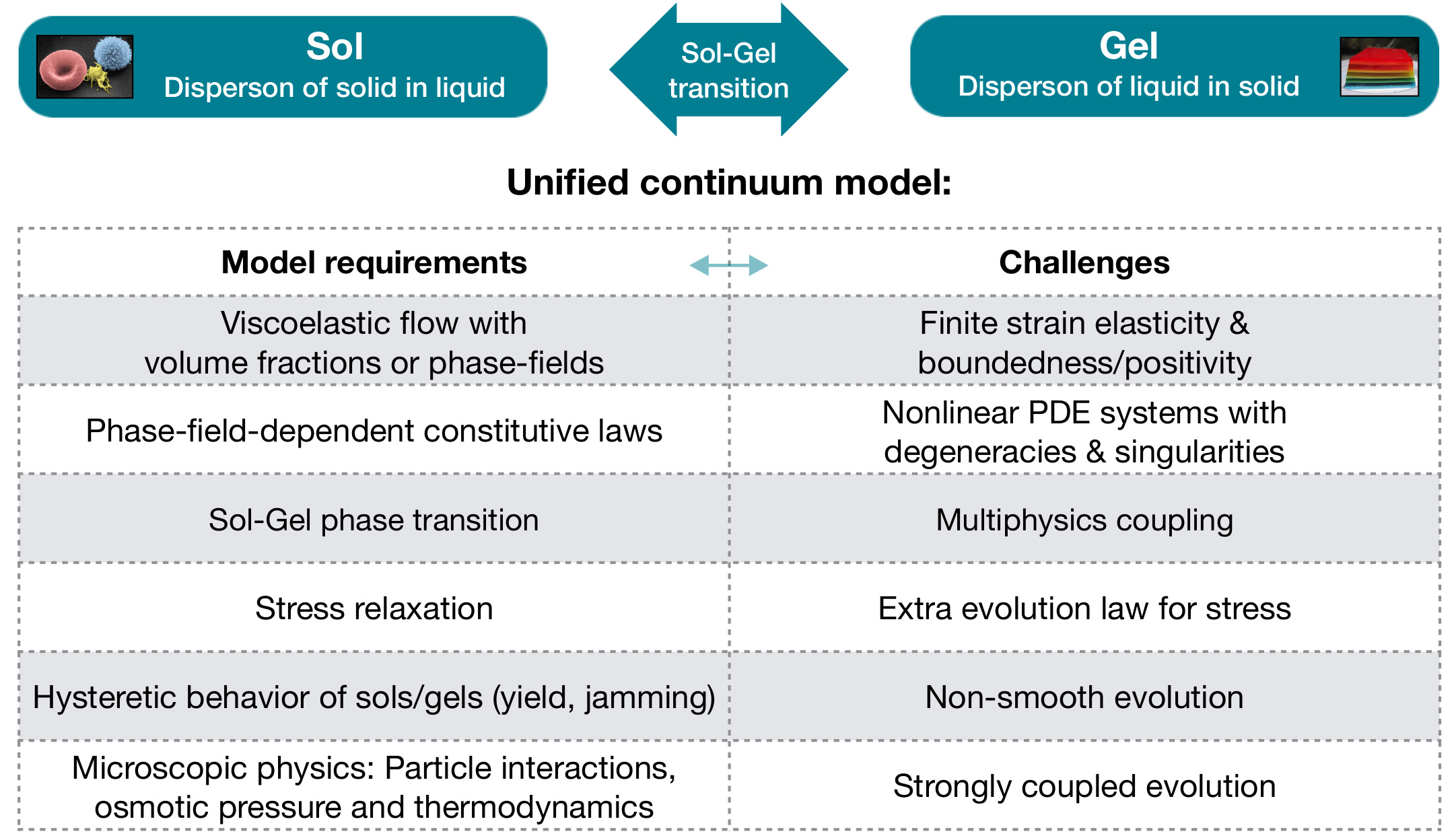
Flows of soft elastic particles suspended in viscous fluids play a fundamental role in biological and geological systems. In microgel suspensions, they offer promising future prospects for engineering and pharmaceutical industries. The viscoelastic properties of these systems vary depending on the particle density: At low densities (dilute regime) mixtures have an effective viscosity and elastic properties are negligible, while for moderate densities (dense regime) particles interact and deform so that the effective flow becomes viscoelastic; such a viscous or viscoelastic suspension is called sol. As the suspension exceeds the dense regime, solid particles become so densely packed that elastic links are formed between them; such a mixture is called gel.
Although this sol-gel transition is not yet well-understood, its vital impact on soft matter, biological or medical applications is evident: Examples are plaque formation and drying blood, where platelets enter a condensed aggregate phase, or suspensions of proteins in electrolyte solutions that are prone to form gels by clustering. For these systems the elasticity enters the models via the elastic properties of the particles themselves and via the rheology of the assembled gel. From a mathematical point of view, these models have an intriguing interplay of Lagrangian and Eulerian descriptions, where the availability of corresponding transformation maps is a central open question. In the proposed project we will develop a unified continuum model based on phase indicators for the fluid and the solid phase that encompasses the behavior of both regimes sol and gel and captures the phase transition from one to the other.
|
|
Goals
|
For both regimes sol and gel it is the goal of the project i) to deduce a unifying continuum model in terms of a gradient, GENERIC or port-Hamiltonian structure, ii) to carry out mathematical analysis based on this structure and to develop structure-preserving numerical methods. This is the basis iii) to validate the model for the different regimes and to identify physical parameters through experimental data generated by the project. The GFZs experimental tectonics laboratory is equipped with particle image velocimetry (PIV) systems and rheometric setups, from which we will investigate material properties and measure dynamic observables directly comparable to simulations.
|
|
Related Publications
| [9] |
Schmeller, L. and Peschka, D. Gradient flows for coupling order parameters and mechanics, WIAS Preprint 2909, 2022, DOI 10.20347/WIAS.PREPRINT.2909
|
| [8] |
Peschka, D., & Heltai, L. (2022). Model hierarchies and higher-order discretisation of time-dependent thin-film free boundary problems with dynamic contact angle. Journal of Computational Physics, 111325, DOI 10.1016/j.jcp.2022.111325
|
| [7] |
Zafferi, A., Peschka, D., & Thomas, M. (2022). GENERIC framework for reactive fluid flows. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, pp. 1-70, DOI 10.1002/zamm.202100254 .
|
| [6] |
Peschka, D., Zafferi, A., Heltai, L., & Thomas, M. (2022). Variational approach to fluid-structure interaction via GENERIC. Journal of Non-Equilibrium Thermodynamics, 47(2), pp. 217-226, DOI 10.1515/jnet-2021-0081
|
| [5] |
Liu, X., Thomas, M., & Titi, E. S. (2022). Well-Posedness of Hibler's Dynamical Sea-Ice Model. Journal of Nonlinear Science, 32(4), pp. 1-31, DOI 10.1007/s00332-022-09803-y
|
| [4] |
M. G. Hennessy, A. Münch, and B. Wagner, Phase separation in swelling and deswelling hydrogels with a free boundary, Physical Review E, 101(3):032501, 2020.
|
| [3] |
D. Peschka, M. Rosenau, Two-phase flows for sedimentation of suspensions, WIAS Preprint 2743, 2020.
|
| [2] |
M.H. Farshbaf-Shaker, M. Thomas, Analysis of a compressible Stokes-flow with degenerating and singular viscosity, WIAS Preprint 2786, 2020.
|
| [1] |
D. Peschka, M. Thomas, T. Ahnert, A. Münch, and B. Wagner, Gradient structures for flows of concentrated suspensions, Springer-CIM Series, 2019.
|
|
Related events
|