Project head:	Thomas Koprucki, Alexander Mielke
Staff:	Oliver Marquardt
Funding period:	January 2019 – December 2020
Application area:	Nano- and optoelectronics (WIAS), Materials, Light, Devices (MATH+)

Introduction

The development of novel electronic devices and light sources requires efficient techniques to model the physical properties of semiconductor nanostructures as accurate as possible. Such models commonly include elastic, piezo– and pyroelectric, electronic, and optical properties which requires the application of a wide range of formalisms during the design process. Continuum formalisms such as linear elasticity theory and six– or eight–band k·p models in combination with envelope functions represent the back bone of semiconductor device modelling for two decades now and were employed to study semiconductor nanostructures of a wide range of shapes, dimensions, and material compositions [1–4]. Despite the great successes of these formalisms in the past, they suffer from different shortcomings, such as so–called spurious solutions [5] or the incapability to describe indirect–gap semiconductors.

Description

We outline a novel tool kit consisting of a finite–element method (FEM), a multi–band k·p model, and a fitting scheme to obtain the respective parameters from up–to–date ab initio band structures. The FEM–based continuum elasticity module allows us to compute the elastic properties of nanostructures of arbitrary material composition, shape, and crystal structure at low computational costs. Once the elastic properties of the system are known, built–in electrostatic potentials are computed by solving the Poisson equation including piezo– and pyroelectric effects. Strain and built–in electrostatic potentials enter a multi–band k·p model implemented within a plane–wave framework [7]. The number of bands involved and thus the level of sophistication on the one hand and the computational effort on the other can be chosen according to the required accuracy and available computational capabilities. As material parameters for models beyond the eight-band k·p formalism are rare, we also introduce a parameter fitting scheme for high–dimensional parameter spaces employing Sobol sequences [8,9] that can employ up–to–date ab initio band structures. This fitting scheme will be generalized and automatized such that it allows to generate electronic band structure parameters for novel materials and k·p models of arbitrary level of sophistication in a computationally efficient manner [10,11].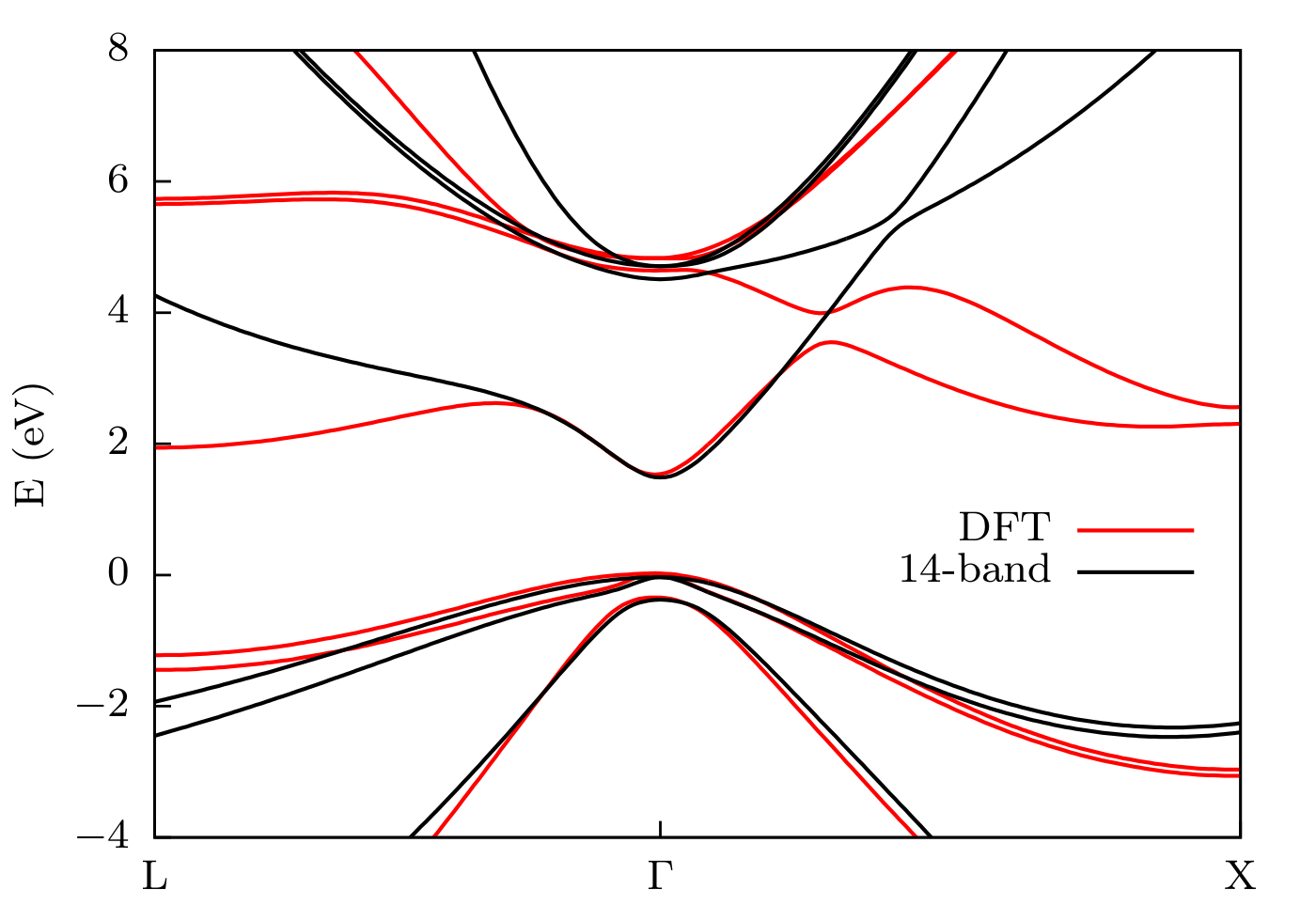

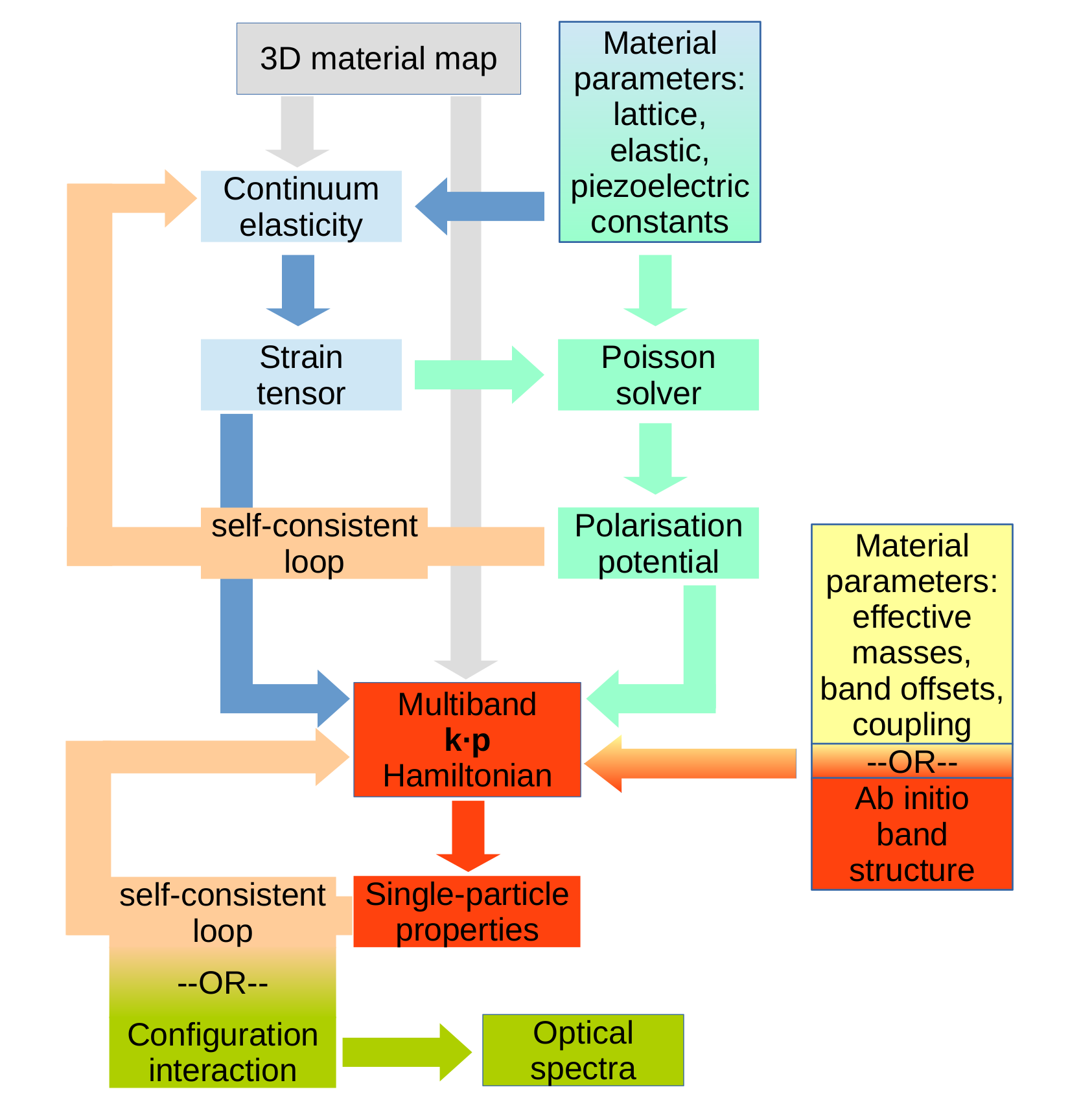
The work flow of a complete simulation of a semiconductor nanostructure is then as follows (cf. Fig. 3): First, a nanostructure of arbitrary shape, size, and material composition is defined in a 3D material map file. Second, the elastic properties are computed using continuum elasticity theory within either a plane–wave or a finite–elements framework. Built–in electrostatic potentials are then computed from the resulting strain distributions, piezo– and pyroelectric constants by solving the Poisson equation. At this point, it is intended to also consider electromechanical coupling, i.e. the influence of such polarization potentials on the elastic properties, within a self–consistent simulation.
Once the elastic properties and built–in potentials are known, they enter a multiband k·p model. Here, the complexity of the model and together with this the accuracy as well as the computational effort are determined by the number of bands involved. The respective Hamiltonian operator is defined by the user in a human–readable meta–language. The required electronic band structure parameters are given in material files for each material involved. At this point, some or all of these parameters can be fitted to most modern ab initio band structures using the above fitting scheme.
With all these ingredients, the Schrödinger equation is solved for a number of electrons and holes. On top of this, excitonic properties can be obtained either using a self–consistent Hartree approach or a configuration–interaction scheme. The output of the final simulation are the optical spectra of the nanostructure.
The combination of the above tools allows us to access a much wider range of possible material systems, crystal structures, and heterostructures for the design of novel devices for optoelectronic applications.

Electronic properties of In(As,Sb,P) graded–composition quantum dots

Graded-composition quantum dots grown using liquid-phase epitaxy techniques in the In(As,Sb,P) material system cover the mid-infrared spectrum (wavelengths of 3 to 5 μm), which is important for a wide range of applications, e.g. in gas sensing or energy harvesting. The particular strength of the growth process from the liquid phase is here that composition gradients through a nanostructure can be intentionally achieved, facilitating the fine-tuning of the optoelectronic properties together with a significant improvement of the crystal quality. In collaboration with researchers from PDI and IKZ Berlin as well as Prof. Karen M. Gambaryan from Yerevan State University, Armenia, who visited WIAS in Summer 2019 funded by DAAD, we have investigated nucleation process and electronic properties of In(As,Sb,P) graded-composition quantum dots in a systematic study. We have computed the electronic properties for different heights and diameters, as observed in the ensemble and combined these results with the experimentally observed diameter distribution to simulate ensemble absorption spectra at room temperature. The simulated absorption peak wavelength (3.829 μm) is in excellent agreement with the experimentally observed one (3.83 μm), facilitating the application of our simulation framework in theory-driven design of In(As,Sb,P) graded-composition quantum dots that fulfill the requirements of specific devices.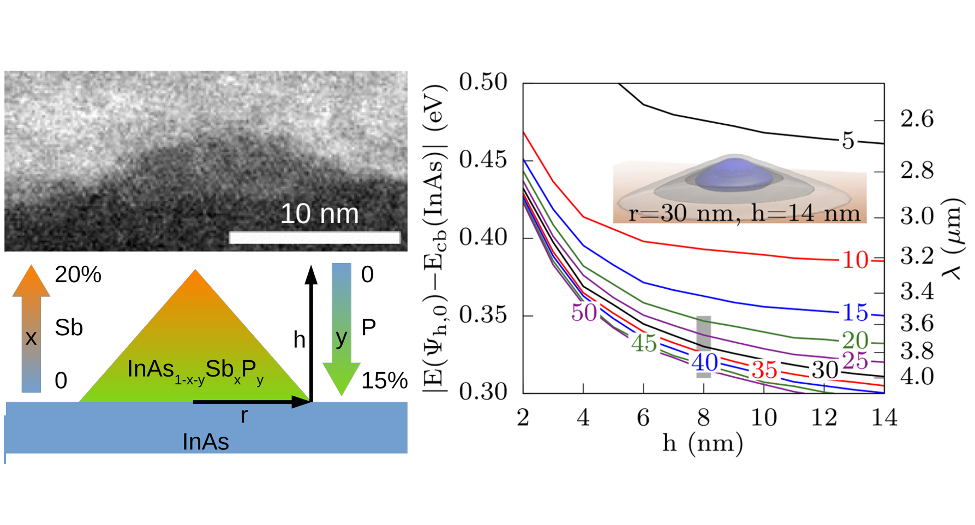

Collaborations

Internal

Timo Streckenbach (RG3),
Jürgen Fuhrmann (RG3),
Peter Mathé (RG6)

External

Jonas Lähnemann, Oliver Brandt, Lutz Geelhaar, Achim Trampert (Paul–Drude–Institut für Festkörperelektronik Berlin),
Torsten Boeck (Institut für Kristallzüchtung Berlin),
Christoph Freysoldt, Jörg Neugebauer (Max–Planck–Institut für Eisenforschung Düsseldorf),
Morten Willatzen (Technical University of Denmark, Lyngby, Denmark and Beijing Institute of Nanoenergy and Nanosystems, Beijing, China),
Migel A. Caro (Aalto University, Finland),
Stefan Schulz (Tyndall National Institute, Cork, Ireland),
Karen M. Gambaryan (Yerevan State University, Armenia)

Project related literature

1. A. D. Andreev and E. P. O'Reilly, “Theory of the electronic structure of GaN/AlN hexagonal quantum dots” Phys. Rev. B 62, 15851 (2000). doi: 10.1103/PhysRevB.62.15851
2. V. A. Fonoberov and A. A. Balandin, “Excitonic properties of strained wurtzite and zinc-blende” J. Appl. Phys. 94, 7178 (2003). doi: 10.1063/1.1623330
3. M. Winkelnkemper, A. Schliwa, and D. Bimberg, “Interrelation of structural and electronic properties in (In,Ga)N/GaN quantum dots using an eight–band k·p model” Phys. Rev. B 74, 155322 (2006). doi: 10.1103/PhysRevB.74.155322
4. M. Ehrhardt and T. Koprucki, eds. Multi–Band Effective Mass Approximations: Advanced Mathematical Models and Numerical Techniques, Lecture Notes Comput. Science Engineering Vol. 94. Springer (2014).
5. R. G. Veprek, S. Steiger, and B. Witzigmann, “Ellipticity and the spurious solution problem of k·p envelope equations” Phys. Rev. B 76, 165320 (2007). doi: 10.1103/PhysRevB.76.165320
6. A.W. Achtstein, O. Marquardt, R. Scott, M. Ibrahim, T. Riedl, A.V. Prudnikau, A. Antanovich, N. Owschimikow, J.K.N. Lindner, M. Artemyev, and U. Woggon: “Impact of shell growth on recombination dynamics and exciton–phonon interaction in CdSe–CdS core–shell nanoplatelets,” ACS Nano 12, 9476–9483 (2018). doi: 10.1021/acsnano.8b04803
7. O. Marquardt, S. Boeck, C. Freysoldt, T. Hickel, S. Schulz, J. Neugebauer, and E. P. O'Reilly “A generalized plane-wave formulation of k·p formalism and continuum elasticity approach to elastic and electronic properties of semiconductor nanostructures” Comp. Mat. Sci. 95, 280 (2014). doi: 10.1016/j.commatsci.2014.06.047
8. I. M. Sobol, “Distribution of Points in a Cube and Approximate Evaluation of Integrals” Zh. Vych. Mat. Mat. Fiz. 7, 784 (1967).
9. H. Niederreiter, “Random Number Generation and Quasi-Monte Carlo Methods”, Society for Industrial and Applied Mathematics (1992).
10. O. Marquardt, P. Mathé, T. Koprucki, M. A. Caro, and M. Willatzen: “Data–driven electronic structure calculations in semiconductor nanostructures – beyond the eight–band k·p formalism”, IEEE, Proceedings of the International Conference on Numerical Simulation of Optoelectronic Devices (2018) doi: 10.1109/NUSOD.2018.8570274
11. O. Marquardt: “Data-driven Electronic Structure Calculations for Nanostructures” NUSOD blog
12. O. Marquardt, P. Mathé, T. Koprucki, M. A. Caro, and M. Willatzen: “Multiband k·p model and fitting scheme for ab initio–based electronic structure parameters for wurtzite GaAs”, Phys. Rev. B 101, 235147 (2020) doi: 10.1103/PhysRevB.101.235147
13. K. M. Gambaryan, T. Boeck, A. Trampert, and O. Marquardt: “Nucleation Chronology and Electronic Properties of In(As,Sb,P) Graded Composition Quantum Dots Grown on an InAs(100) Substrate”, ACS Applied Electronic Materials 2, 646 (2020) doi: 10.1021/acsaelm.9b00739