ECMath Project SE8:
Stochastic methods for the analysis of lithium-ion batteries

Project heads	Wolfgang Dreyer and Peter Friz
Staff	Paul Gajewski and Mario Maurelli
Internal cooperation	SE4 (Kraus, Kutyniok, Wagner)
External cooperation	Clemens Guhlke (WIAS), Michael Herrmann (Uni Saarbrücken), Virtual Vehicle Compentence Center, Graz

This research is carried out in the framework of Matheon supported by Einstein Foundation Berlin.

---

Project background

Currently lithium-ion batteries are the most promising storage devices to store and convert chemical energy into electrical energy and vice versa. An important class of modern lithium batteries contain electrodes that consist of a powder of 10¹⁰ - 10¹⁷ nano-particles on a substrate. During the charging process of a battery, lithium atoms are reversibly stored in the ensemble of nanosized storage particles which undergo a phase transition. However, the kind of phase transition was unclear until 2010. The MATHEON project C26 confirmed that the phase transition occurs within the particle ensemble and not, as previously assumed, in the single particles. The original model of C26 is a single nonlinear and nonlocal Fokker-Planck equation for a probability density, while in the current project SE8 a related coupled system of stochastic differential equations is proposed. From the technological point of view the research project addresses the improvement of many-particle electrodes of lithium-ion batteries.

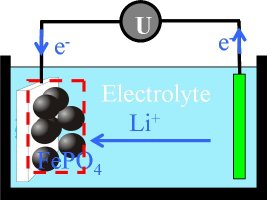Figure 1: Sketch of a lithium-ion battery (LiFePO4).

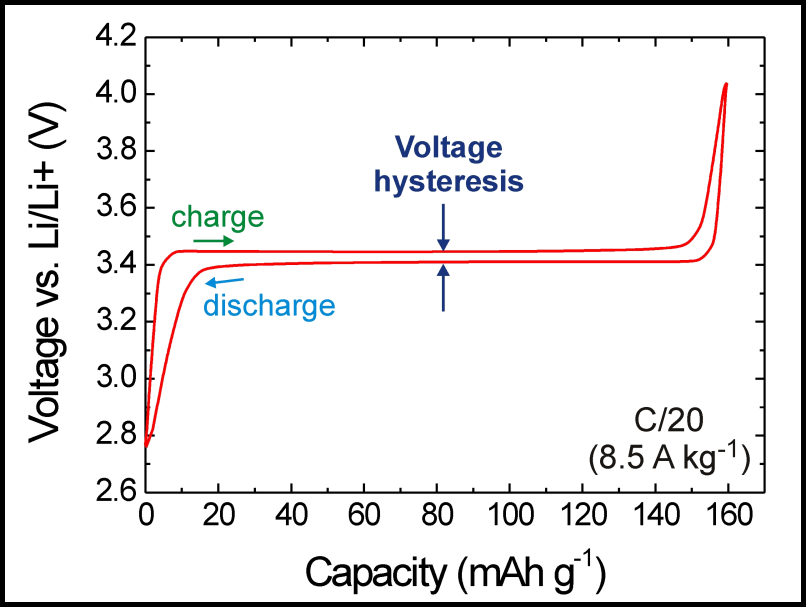Figure 2: Typical voltage-capacity-diagram of a lithium-ion battery [R4].

Advantages of the SDE-model

A detailed study of the Fokker-Planck equation has led to the conjecture that the corresponding SDE system has better properties to predict the intricate phenomena during the charging process.

(FP)

(SDE)

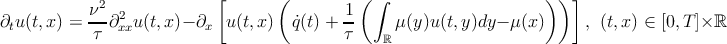
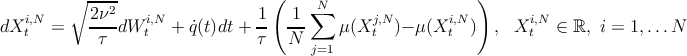
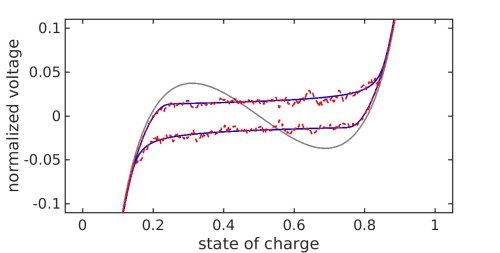
Figure 3: Simulation of the voltage-capacity-diagram. blue: Fokker-Planck-model, red: SDE-Model, grey: chemical potential single particle.

• The two small parameters τ and ν induce numerical difficulties which can be avoided in the SDE setting.
• The Fokker-Planck equation describes the slow charging process. An extension of the model to charging in seconds is very involved for Fokker-Planck but simple in the SDE case.
• Coupling of electrolyte and cathode is easier with the SDE model.
• Typical cathodes contain storage particles with variable size. This important feature can be included into the model by introducing a dependence on particle size for τ and ν. This modification is relatively easy to implement for the SDE system and the corresponding simulations done in the project are in good agreement with experimental observations.

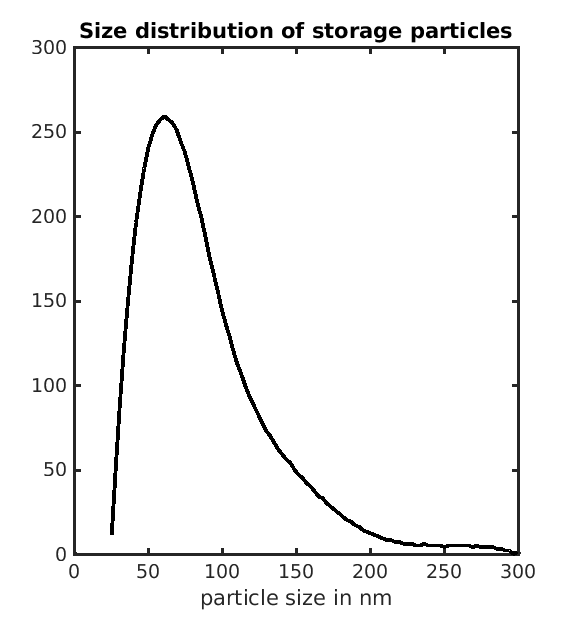
Figure 4: Realistic particle size distribution used in the simulation.

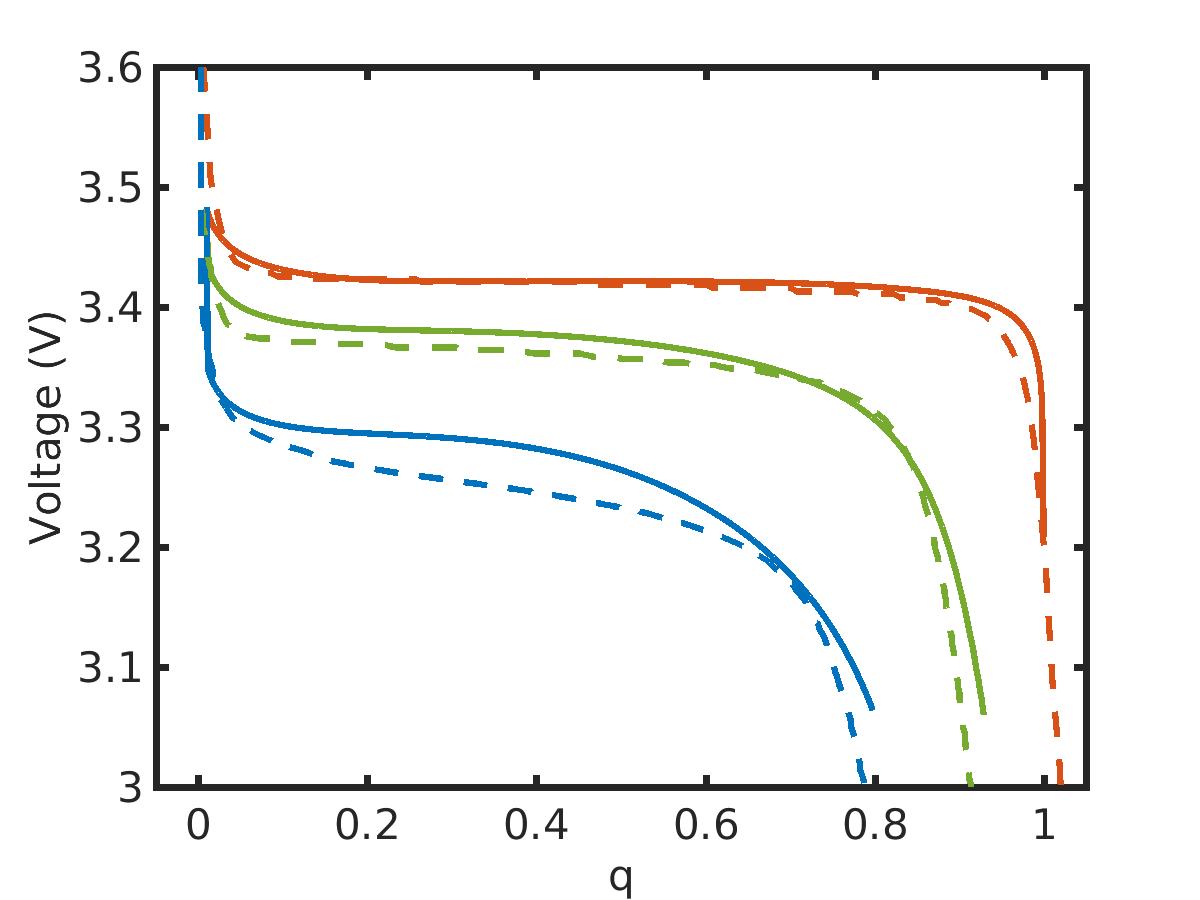
Figure 5: Comparison with experiments. Continuous line: simulations, dashed line: experiments. Charging rates 1/25C (red), 1C (green), 3C (blue).

Simulations reproduce the experimental observation that small particles are filled with Lithium before larger particles are filled.

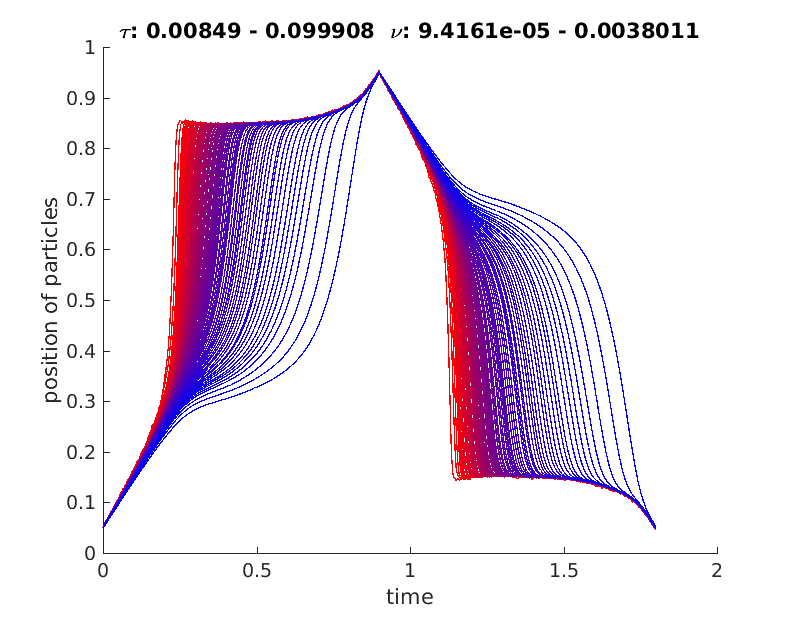
Figure 6: Loading path of 100 sample particles. red: smallest particles (25 nm), blue: largest particles (300 nm)

It was also observed in simulations that a shift or stretch the distribution of the particle size and a change in the charging rate have relevant impact on the capacity and the efficiency of the battery [R0].

Mathematical details

In the case of single size particles (τ and ν fixed), well-posedness of both the Fokker-Planck equation and of the SDE system, and convergence of the SDE system to the Fokker-Planck equation, in a suitable sense, hold (see e.g.[R7]). More precisely, the (random) empirical measure

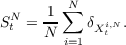
converges (weakly in space) to the solution to the Fokker-Planck equation, as the number of particles N tends to ∞. This brings the so-called “propagation of chaos” (asymptotic independence of two particles) and can be enforced including a large deviation result. The case with boundary conditions is to be investigated.

The convergence statement is relevant because it implies the convergence of the voltage coming from the SDE system to the voltage from the Fokker-Planck equation. This allows to use the SDE system as approximation to the Fokker-Planck equation, and implies also stability of simulations for the SDE system, for large number of particles. Simulations to SDE system are performed easily through Euler scheme.

This framework can be suitably extended to the case of variable size particles. In this case the SDE modelling can also provide justification of the dependence of the noise on the particle size.

An interesting phenomenon observed in simulations is the phase transition that occurs for small τ and ν (see [R5,R6]): different ratios between these two parameters bring different behaviours of the voltage (this depends actually also on the size distribution). We aim at analyze this phenomenon through the SDE system.

References

[R0]	Dreyer, Friz, Gajewski, Guhlke, and Maurelli. Stochastic model for LFP-electrodes, WIAS preprint 2329 (2016).
[R1]	Dreyer, Gaberšček, Guhlke, Huth, and Jamnik. Phase transition and hysteresis in a rechargeable lithium battery revisited. European J. Appl. Math., 22:267-290, 2011.
[R2]	Dreyer, Guhlke, and Herrmann. Hysteresis and phase transition in many-particle storage systems. Contin. Mech. Thermodyn., 23(3):211-231, 2011.
[R3]	Dreyer, Guhlke, and Huth. The behavior of a many particle cathode in a lithium-ion battery. Phys. D, 240:1008-1019, 2011.
[R4]	Dreyer, Jamnik, Guhlke, Huth, Moškon, and Gaberšček. The thermodynamic origin of hysteresis in insertion batteries. Nat. Mater., 9:448-453, 2010.
[R5]	Herrmann, Niethammer and Velázquez. Kramers and non-Kramers phase transitions in many-particle systems with dynamical constraint. Multiscale Model. Simul. 10(3):818–852, 2012.
[R6]	Herrmann, Niethammer and Velázquez. Rate-independent dynamics and Kramers-type phase transitions in nonlocal Fokker-Planck equations with dynamical control. Arch. Ration. Mech. Anal. 214(3):803–866, 2014.
[R7]	Sznitman, Topics in propagation of chaos. École d’Été de Probabilités de Saint-Flour XIX – 1989, 165–251, Lecture Notes in Math., 1464, Springer, Berlin, 1991.