ECMath project SE18 "Models for heat and charge-carrier flow in organic electronics"
Project heads
Annegret Glitzky and Matthias Liero
Staff
Collaboration
Jürgen Fuhrmann, Thomas Koprucki
External Cooperation
Axel Fischer,
Reinhard Scholz,
Michael Sawatzki, Hans Kleemann
from Dresden Integrated Center for Applied Physics and Photonic Materials (IAPP, TU Dresden)
Internal Cooperation
- SE23: Multilevel adaptive sparse grids for parametric stochastic simulation models of charge transport (Sebastian Matera)
- SE20: Exciton dynamics in organic semiconductors (Rupert Klein)
- OT8: Modeling, analysis, and optimization of optoelectronic semiconductor devices driven by experimental data (Marita Thomas)
- CH11: Sensing with nanopores (Jürgen Fuhrmann, Clemens Guhlke)
- OT-AP1: Multi-dimensional modeling and simulation of electrically pumped semiconductor-based emitters (Uwe Bandelow, Thomas. Koprucki, Alexander Mielke, Frank Schmidt (B4 of CRC 787))
- Effective models for interfaces with many scales (C05 of CRC 1114 Alexander Mielke)
This research is carried out in the framework of Matheon supported by Einstein Foundation Berlin


Project background
Organic electronics using carbon-based semiconductor materials surround us in our everyday life, e.g., in smartphone displays or solar cells. On the one hand, the technological adaption to other applications such as advanced lighting applications and thin-film transistors is still at an early stage. On the other hand, the tremendously fast pace in the development of new organic materials with fine-tuned properties yields the potential for smart 3D vertical structures with the desired electronic behavior.
A characteristic property of all organic semiconductor materials is the carrier flow by means of a temperature-activated hopping (cf. [Kordt et al. 2015] between adjacent molecules. This leads in connection with Joule self-heating to a strong positive feedback loop between power dissipation, temperature, conductivity, and current flow, resulting in a complicated nonlinear behavior in devices such as hysteresis, see [Fischer et al. 2014] and [Fischer et al. 2013]. In Matheon project D-SE2 , we developed a PDE thermistor model with effective material laws (cf. [Liero et al. 2015] and [Fuhrmann et al. 2017]) to describe the interplay of the total electrical current and the heat flow. However, electronic details such as electron and hole flow, recombination, and energy barriers at material interfaces are neglected.
Aims of the project
To be more predictive with respect to diode behavior of advanced OLED concepts or current paths in small scale devices like organic transistors (cf. [Kaschura et al. 2016]), a more microscopic description incorporating electron and hole currents, recombinations (cf. [van der Holst et al. 2009]), and heterostructures is needed. A characterization of the behavior should be entirely based on the geometric structure and on the individual properties of each material layer.
The aim of the project is to develop a thermodynamically correct energy-drift-diffusion model for organic semiconductor devices and its discretization and implementation in a simulation tool. The outcome of the project is a fundamental building block for a more efficient multi-scale and multi-physics description and simulation of organic devices.
First, the transport of charge carriers in the isothermal case will be described on the basis of a drift-diffusion model, taking the distinctive features of organic materials into account. Second, the model will be extended in a thermodynamically consistent way to include the self-heating and the resulting feedback as well. In both points, the aspects of modeling, analysis, numerics, and simulation are considered.
The approximation of drift-diffusion fluxes should be based on generalized Scharfetter-Gummel schemes for problems with diffusion enhancement (cf. [Koprucki et al. 2014] and [Farrell et al. 2016]).
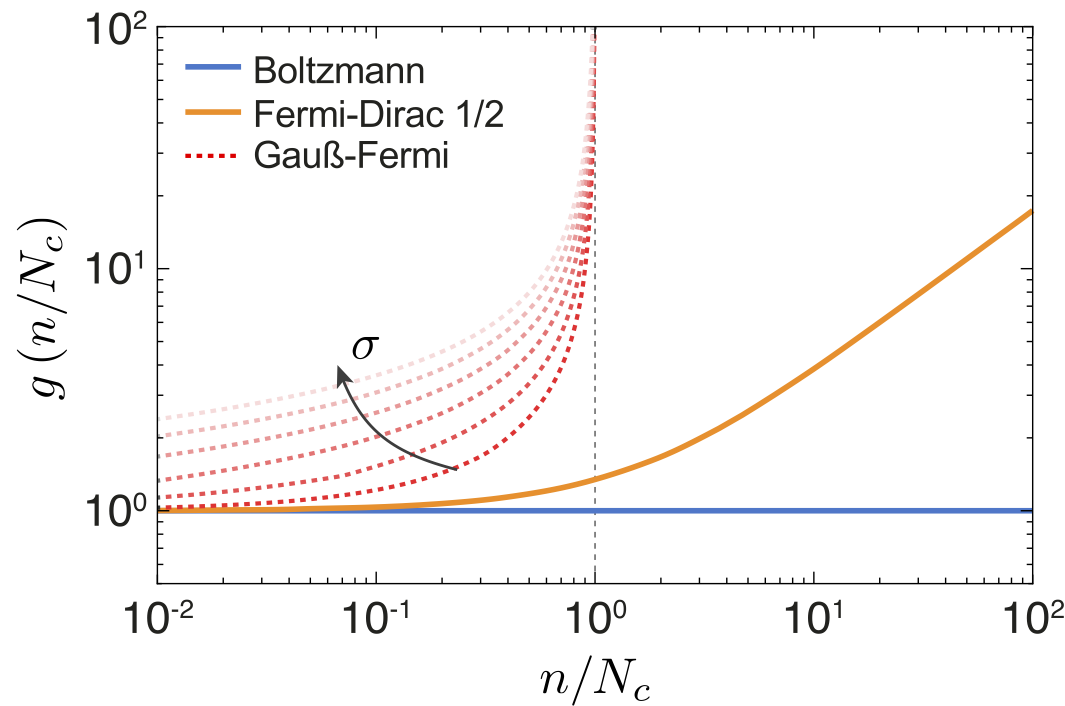
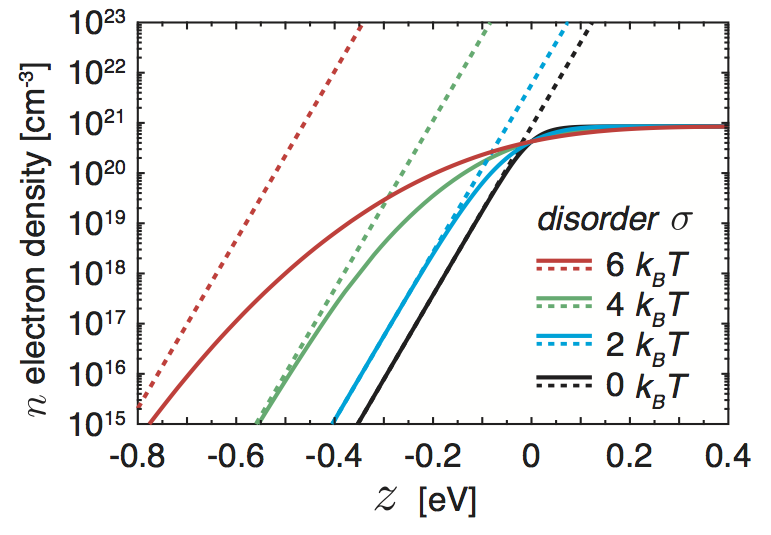
There are several mathmatical challenges regarding a drift-diffusion description of organic devices: In organic semiconductors, the energy levels are Gaussian-distributed with disorder parameter σ such that the densities of electrons and holes are described by the Gauss-Fermi integrals (cf. [Paasch et al. 2010]) . This leads to a generalized Einstein relation and results in a nonlinear diffusion enhancement (cf. [van Mensfoort et al. 2008]) in the relation between drift and diffusion current. Moreover, the mobility functions for organic semiconductor materials with Gaussian disorder are increasing with respect to temperature, carrier density, and electrical field strength.
Highlights
We organized the workshop AMaSiS 2018 — Applied Mathematics and Simulation for Semiconductors at WIAS Berlin from October 8-10, 2018. The workshop homepage is here: Link. We gratefully acknowledge the support by ECMath and DFG.
Project related literature
Recent results of project
- Full electrothermal OLED model including nonlinear self-heating effects, Phys. Rev. Applied, Volume 10, pp. 014023, 2018, DOI: 10.1103/PhysRevApplied.10.014023
- Balance of horizontal and vertical charge transport in organic field-effect transistors, Phys. Rev. Applied, Volume 10, pp. 034069, 2018
- Instationary drift-diffusion problems with Gauss-Fermi statistics and field-dependent mobility for organic semiconductor devices, Preprint 2523, WIAS Berlin, 2018, to appear in Comm. Math. Sci.
- Drift-diffusion modeling, analysis and simulation of organic semiconductor devices, Preprint 2493, WIAS Berlin, 2018.
- Hybrid finite-volume/finite-element schemes for p(x)-Laplace thermistor models, Finite Volumes for Complex Applications VIII - Hyperbolic, Elliptic and Parabolic Problems: FVCA 8, Lille, France, pp. 397-405, 2017, DOI: 10.1007/978-3-319-57394-6
- 3D electrothermal simulations of organic LEDs showing negative differential resistance, Opt. Quantum Electron., Volume 49, pp. 330/1-330/8, 2017, DOI: 10.1007/s11082-017-1167-4
- Modeling and simulation of electrothermal feedback in large-area organic LEDs 2017 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Copenhagen, 2017, pp. 105-106, DOI: 10.1109/NUSOD.2017.8010013
Further references
- Operation mechanism of high performance organic permeable base transistors with an insulated and perforated base electrode, J. Appl. Phys., 120, pp. 094501/1–094501/8, 2016, DOI: 10.1063/1.4962009
- Mathematical Methods: Drift-Diffusion Models. In J. Piprek (ed.), Handbook of Optoelectronic Device Modeling and Simulation, volume 2, chapter 50, pp. 733–771. CRC Press, 2017, WIAS preprint 2263
- OLEDs: light-emitting thin film thermistors revealing advanced self-heating effects, Proc. SPIE, 9566, 95661A–95661A-7, 2015, DOI: 10.1117/12.2186940
- p-Laplace thermistor modeling of electrothermal feedback in organic semiconductors, Zeitschrift für angewandte Mathematik und Physik, Volume 66, pp. 2957–2977, 2015, DOI: 10.1007/s00033-015-0560-8
- Modeling of Organic Light Emitting Diodes: From Molecular to Device Properties, Adv. Funct. Mater., Volume 25, pp. 1955–1971, 2015, DOI: 10.1002/adfm.201403004
- On thermodynamic consistency of a Scharfetter-Gummel scheme based on a modified thermal voltage for drift-diffusion equations with diffusion enhancement, Optical and Quantum Electronics, Volume 47, pp. 1327–1332, 2015, DOI: 10.1007/s11082-014-0050-9
- Feel the heat: Nonlinear electrothermal feedback in Organic LEDs, Advanced Functional Materials, Volume 24, pp. 3367–3374, 2014, DOI: 10.1002/adfm.201303066
- Self-heating, bistability, and thermal switching in organic semiconductors, Phys. Rev. Lett., Volume 110, pp. 126601, 2013, DOI: 10.1103/PhysRevLett.110.126601
- Charge carrier density of organics with Gaussian density of states: Analytical approximation for the Gauss-Fermi integral, Journal of Applied Physics, Volume 107, pp. 104501, 2010, DOI: 10.1063/1.3374475
- Electron-hole recombination in disordered organic semiconductors: Validity of the Langevin formula, Phys. Rev. B, Volume 80, pp. 235202, 2009, DOI: 10.1103/PhysRevB.80.235202
- Effect of Gaussian disorder on the voltage dependence of the current density in sandwich-type devices based on organic semiconductors, Phys. Rev. B, Volume 78, pp. 085207, 2008, DOI: 10.1103/PhysRevB.78.085207


