

ECMath Project SE17:
Stochastic methods for the analysis of lithium-ion batteries
| Project heads | Jean-Dominique Deuschel, Wolfgang Dreyer, Peter Friz, Clemens Guhlke |
| Staff | Mario Maurelli |
Project background
Currently lithium-ion batteries are the most promising storage devices to store and convert chemical energy into electrical energy and vice versa. An important class of modern lithium batteries contain electrodes that consist of a powder of 10 10 - 1017 nano-particles on a substrate. During the charging process of a battery, lithium atoms are reversibly stored in the ensemble of nanosized storage particles which undergo a phase transition. The phase transition occurs within the particle ensemble and not, as previously assumed, in the single particles [DJGHMG10]. In the original model the phase transition is described by a single nonlinear and nonlocal Fokker-Planck equation for a probability density [DGHe11]. In the previous project SE8 a related coupled system of stochastic differential equations is derived. From the technological point of view the research project addresses the improvement of many-particle electrodes of lithium-ion batteries.
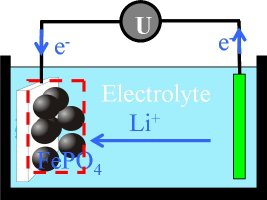 Figure 1: Sketch of a lithium-ion battery (LiFePO4). |
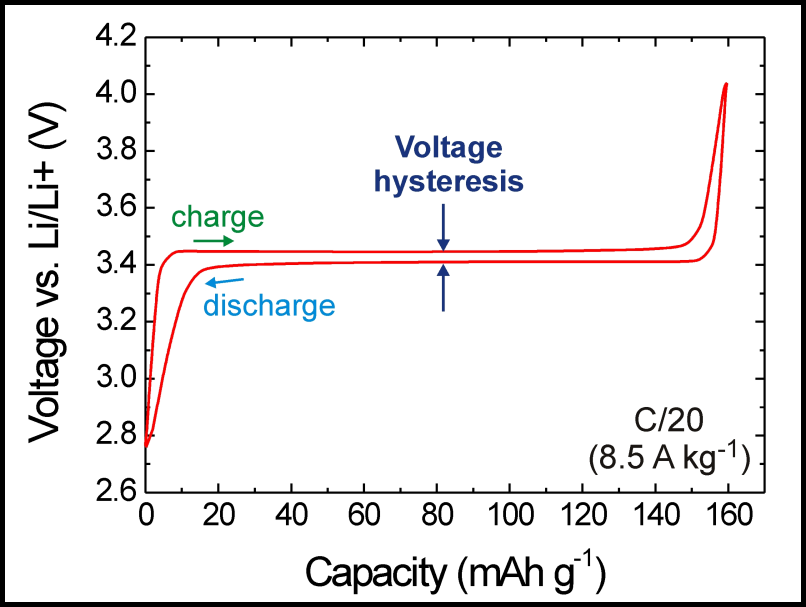 Figure 2: Typical voltage-capacity-diagram of a lithium-ion battery [DJGHMG10]. |
Achievements of previous ECMath SE8 project
The main achievement of the previous ECMath SE8 project (June 2014 - May 2017) was the derivation of mathematical model for a many particle electrodes within the context of non-equilibrium thermodynamics, which generalized the Fokker-Planck model [GGMFD16+]. Prominent features of this model are:
- The model fits (qualitatively) the experimental data, at least for slow and moderate charging regime, by using only two constant parameters.
- The model gives an explanation for the hysterical behavior observed in lithium-ion batteries.
- The model allows to study particle size distribution on the rate dependent capacity and efficiency of the battery.
From the mathematical perspective, the main tool for the project was the passage from the Fokker-Planck (PDE) setting to the stochastic differential equation (SDE) setting, more precisely to a so-called McKean-Vlasov SDE and related mean field interacting particle system (see [S91]). This is particularly useful here: 1) It allows fast simulations, compared to standard parabolic PDE numerical tools due to small viscosity. This simulations proved to be stable even for a relatively low number of particles, which made them easily treatable. 2) The interacting particle system is capable to incorporate further physical phenomena and to extend the electrode model to a full battery model, e.g. coupling to the electrolyte, surface reaction, elastic deformation and heat production and transport. The McKean-Vlasov SDE theory has given input for further theoretical research on asymptotic analysis, see [DFMS16+] on a large deviations analysis.
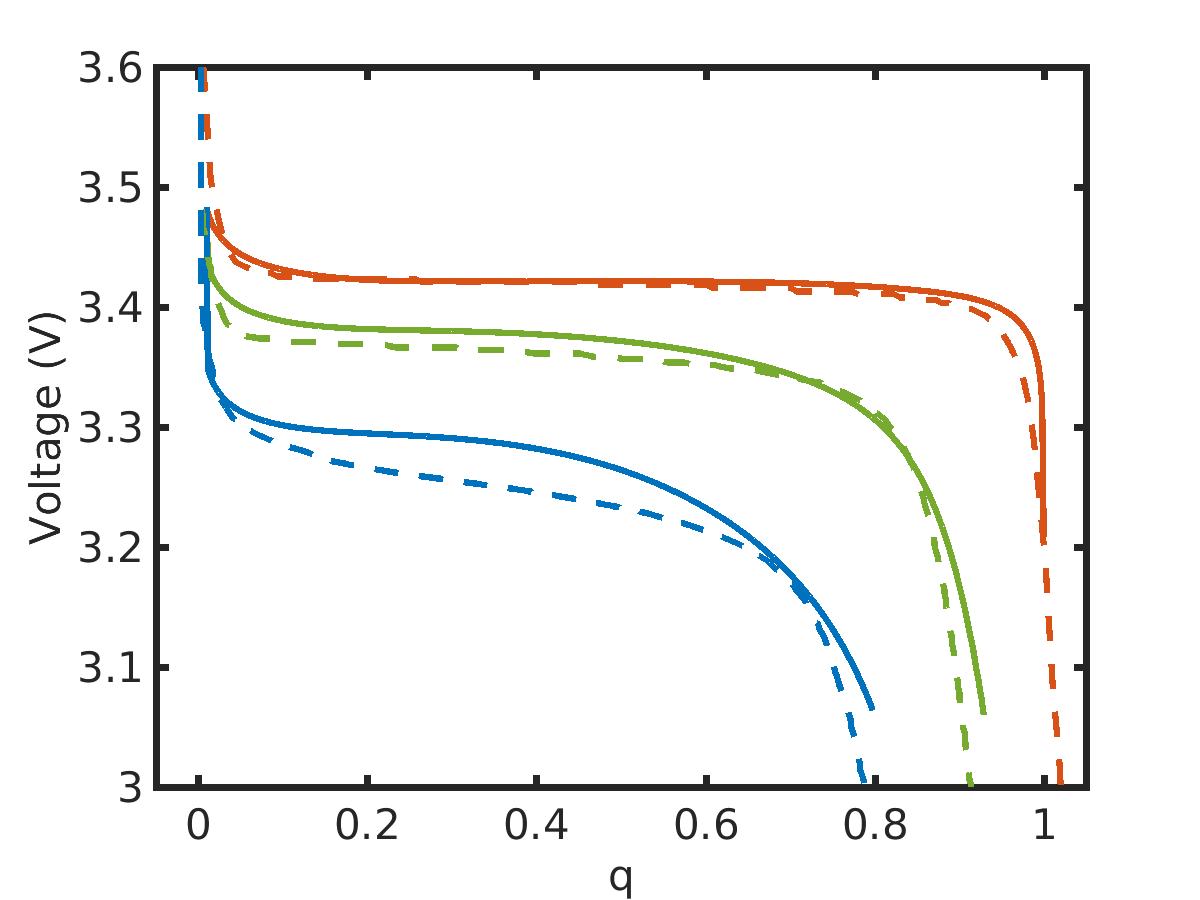 Figure 3: Comparison with experiments. Continuous line: simulations, dashed line: experiments. Charging rates 1/25C (red), 1C (green), 3C (blue) [GGMFD16+]. |
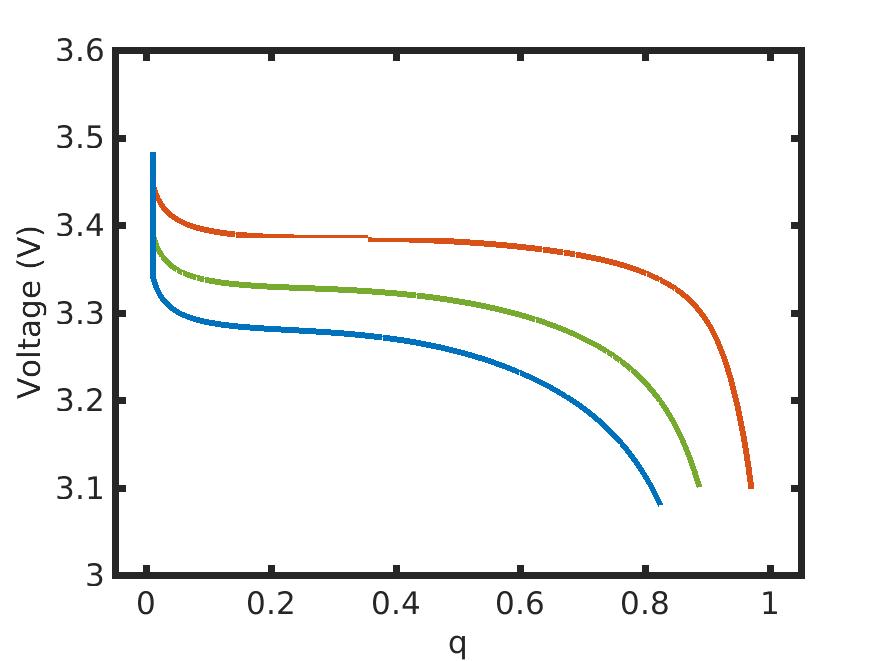 Figure 4: Impact of particle size distribution on battery voltage. Particle size distribution: 25-400nm (red), 25-1000nm (green), 25-1500nm (blue) [GGMFD16+]. |
The many-particle model
We focus on a lithium-ion battery cathode, which contains of many iron phosphate (FePO4) particles. During the discharge (resp. charge) process, these particles get filled (resp. depleted) with lithium atoms. The description of the filling degree Xi∈(0,1) in the i-th particle is the object of the model, as the output voltage of the battery can be related to the average filling degree q∈(0,1). Each Xi filling degree evolves accordingly to
dXi = (τi)-1 (-μ(Xi) +μs)dt +2νi(τi)-1/2 dWi -(τi)-1dZ
with the constraintq(t) = ∑ υi Xi(t) .
Here μ(Xi) is the chemical potential in the bulk of the particle, υi, τi and νi are numbers related to the particle size distribution and to two constant parameters τ0 and ν0, which can be tuned. The parameter τ0 is related to the intercalation rate of lithium into the particles and ν0 controls the strength of microscopic fluctuations within the particle system. Here μs is the surface chemical potential and plays the role of a Lagrange multiplier for the constraint. The noise is modeled via independent real Wiener processes. Z is needed for the constraints. The current is linked to the time derivative of the average filling degree and the voltage is determined by the surface chemical potential μs. The full model is described in [GGMFD16+].Aims of ECMath SE17 project
The previous model have some drawbacks in the fast charging regime, namely: it does not fit well the experimental data and simulations are not easily accessible, due to the fact that electrode is almost filled or empty. Note that this regime is relevant for applications for example in the automotive industry. The aim of SE17 project is to investigate the fast charging regime and get a more realistic model, which helps understanding the behavior of lithium-ion batteries in this regime.- We aim at a theoretical and numerical study for the system close to boundaries, that is Xi close to 0 or 1. that is X^i close to 0 or 1 rather than q. A related question is the specific form of the noise close to the boundaries, as we would like to understand the influence of the noise.
- We aim at incorporating new features, like volume expansion of the particles due to the lithium intercalation process, non-linear constitutive relations of Butler-Volmer type, and comparing the simulations results with the ones from the previous model and experiments.
Mathematical details
From the simulation viewpoint, the main challenge is how to simulate the process when the filling degrees Xi come close to the boundaries 0 or 1. This is an issue even without noise, when the system is easily well-posed. From the theoretical viewpoint, we have to combine the interaction term built in the model and the boundary terms. This does not fall in previously studied case in [S84].References
| [DFMS16+] | Deuschel, Friz, Maurelli, Slowik. The enhanced Sanov theorem and propagation of chaos. To appear on Stoch. Proc. Appl., arXiv preprint 1602.08043 (2016). |
| [DGGHJ11] | Dreyer, Gaberšček, Guhlke, Huth, and Jamnik. Phase transition and hysteresis in a rechargeable lithium battery revisited. European J. Appl. Math., 22:267-290, 2011. |
| [DGHe11] | Dreyer, Guhlke, and Herrmann. Hysteresis and phase transition in many-particle storage systems. Contin. Mech. Thermodyn., 23(3):211-231, 2011. |
| [DGHu11] | Dreyer, Guhlke, and Huth. The behavior of a many particle cathode in a lithium-ion battery. Phys. D, 240:1008-1019, 2011. |
| [DJGHMG10] | Dreyer, Jamnik, Guhlke, Huth, Moškon, and Gaberšček. The thermodynamic origin of hysteresis in insertion batteries. Nat. Mater., 9:448-453, 2010. |
| [GGMFD16+] | Guhlke, Gajewski, Maurelli, Friz, Dreyer. Stochastic model for LFP-electrodes. To appear on Contin. Mech. Thermodyn., WIAS preprint 2329 (2016). |
| [S91] | Sznitman, Topics in propagation of chaos. École d’Été de Probabilités de Saint-Flour XIX – 1989, 165–251, Lecture Notes in Math., 1464, Springer, Berlin, 1991. |
| [S84] | Sznitman, Nonlinear reflecting diffusion process, and the propagation of chaos and fluctuations associated. J. Funct. Anal. 56(3), 311-336, 1984. |

