
DFG Priority Programme 1748:
Reliable Simulation Techniques in Solid Mechanics. Development of Non-standard Discretisation Methods, Mechanical and Mathematical AnalysisSubproject BV-FEM:
Finite element approximation of functions of bounded variation
and application to models of damage, fracture, and plasticity
Project Head: Dr. Marita Thomas (in collaboration with Prof. Dr. Sören Bartels, U Freiburg)
Investigator: Marijo Milicevic
Funding period: October, 2014 - September, 2017
Description
The aim of this project is to establish reliable and efficient numerical methods for models of solids with spatial discontinuities caused by the evolution of dissipative processes such as plasticification, damage or fracture. In particular, the project focuses on such prototypical models that use the class of BV-functions to mathematically describe the discontinuities, that are guaranteed to converge to a solution of the infnite-dimensional model and for which iterative solution methods can be constructed. Emphasis is on unregularized numerical approaches that lead to sharp approximations of discontinuities on coarse grids and rigorous convergence proofs. Some typical and guiding principles can be seen in the following examples:
- A hardening regularization of perfectly plastic materials leads to a strong regularization of shear bands:
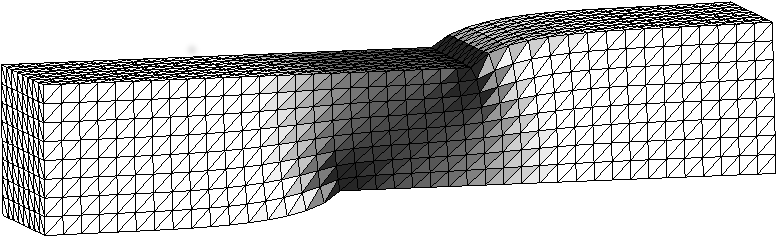
(Figure from: S. Bartels, Numerical methods for nonlinear partial differential equations, Springer Series in Computational Mathematics, 47, Springer, 2015.)
- local, adaptive refinement strategies allow accurate approximations of discontinuities:

(Figure from: S. Bartels: Error control and adaptivity for a variational model problem defined on functions of bounded variation,
Math. Comp. (accepted))
- subdifferential flows define discontinuous evolutions:
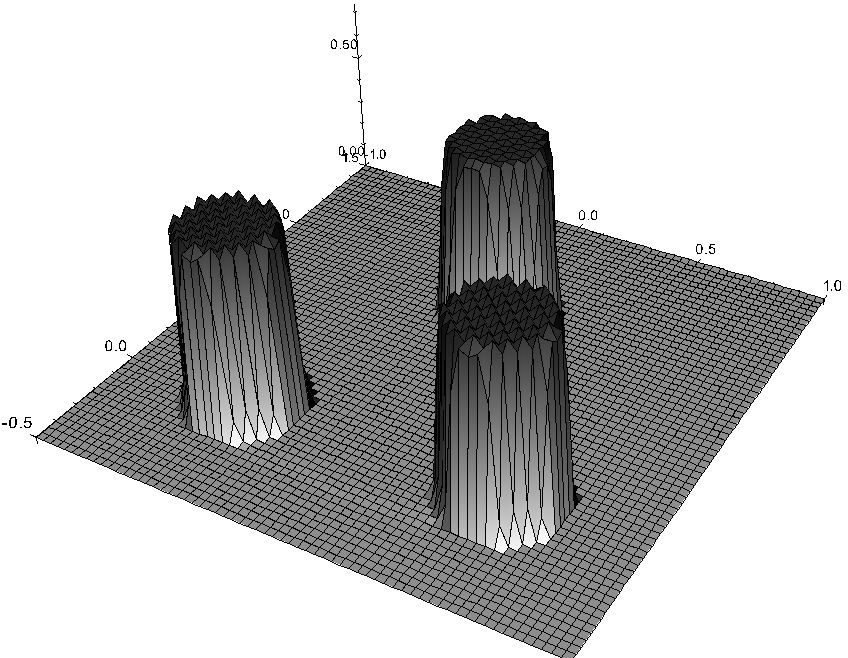
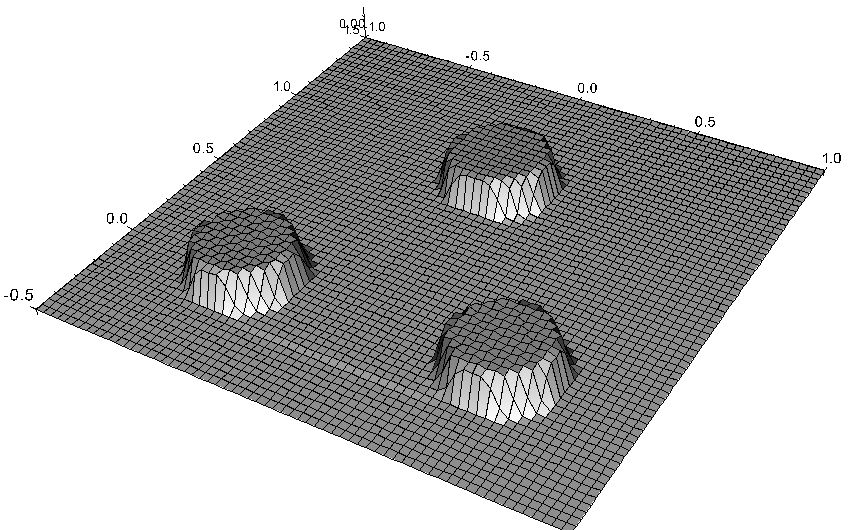
(Figure from: S. Bartels, R. H. Nochetto, and A. J. Salgado: Discrete total variation flows without regularization.
SIAM J. Numer. Anal. 52(1), 363-385, 2014.)
The main objectives of the research project are the development, analysis, and implementation of finite element methods for model problems describing discontinuities in BV. This includes the derivation of a priori and a posteriori error estimates as well as the construction of adaptive and extended approximation methods for BV-prototype models such as the Rudin-Osher-Fatemi and the Mumford-Shah model.
The techniques will be transferred to analytically justified and closely related models for the description of rate-independent inelastic processes, in particular perfect plasticity, damage and fracture. The methods and results will be applied to particular model scenarios and benchmark problems in mechanics.
Publications
- M. Thomas, C. Bilgen and K. Weinberg: Analysis and simulations for a phase-field fracture model at finite strains based on modified invariants
(WIAS Preprint 2456).- R. Rossi and M. Thomas: From nonlinear to linear elasticity in a coupled rate-dependent/independent system for brittle delamination. (WIAS-Preprint 2409).
- M. Thomas: A comparison of delamination models: Modeling, properties, and applications Appeared in: Mathematical Analysis of Continuum Mechanics and Industrial Applications II, Proceedings of the International Conference CoMFoS16, P. van Meurs, M. Kimura, H. Notsu, eds., vol. 30 of Mathematics for Industry, Springer, Singapore, pp. 27--38, 2017.
- S. Bartels, M. Milicevic, and M. Thomas: Numerical approach to a model for quasistatic damage with spatial BV-regularization. (WIAS-Preprint 2388).
- M. Thomas and C. Zanini: Cohesive zone-type delamination in visco-elasticity. Discr. Contin. Dyn. Syst. Ser. S 10:1487--1517, 2017. (WIAS-Preprint 2350).
- R. Rossi and M. Thomas: From adhesive to brittle delamination in visco-elastodynamics. Math. Models Methods Appl. Sci., 27:1489--1546, 2017. (WIAS-Preprint 2259).
- R. Rossi and M. Thomas: Coupling rate-independent and rate-dependent processes: Existence results. SIAM J. Math. Anal., 49(2):1419--1494, 2017. (WIAS-Preprint 2123).
- S. Bartels and Marijo Milicevic: Alternating direction method of multipliers with variable step sizes. ArXiv e-print 1704.06069, 2017.
- S. Bartels and Marijo Milicevic: Iterative solution of a constrained total variation regularized model problem. Discr. Contin. Dyn. Syst. Ser. S (accepted), 2016. (pdf)
- S. Bartels and Marijo Milicevic: Stability and experimental comparison of prototypical iterative schemes for total variation regularized problems, Computational Methods in Applied Mathematics 16(3):361-388. (pdf)
Events
- July 18-22, 2016: Minisymposium Nonsmooth PDEs in the modeling damage, delamination, and fracture
at the 7ECM: 7th European Congress of Mathematics (Berlin, Germany).- July 1-5, 2016: Special Session Rate-dependent and rate-independent evolution problems in continuum mechanics: Analytical and numerical aspects at the 11th AIMS Conference on Dynamical Systems, Differential Equations and Applications (Orlando, USA).
- September 7-11, 2015: 2nd Summer School of the GAMM-Juniors, SAMM 2015 -- Materials with disconinuities, U Stuttgart.
- August 10-14, 2015: Minisymposium Analysis of nonsmooth PDE systems with applications to material failure
at the ICIAM 2015 (Beijing, China).
Preliminary Work
- M. Thomas: Uniform Poincaré-Sobolev and relative isoperimetric inequalities for classes of domains.
To appear in Discrete Continuous Dynamical Systems, Series A 35:2741--2761, 2015. (WIAS Preprint 1797)- R. Rossi and M. Thomas: From an adhesive to a brittle delamination model in thermo-visco-elasticity.
ESAIM Control Optim. Calc. Var., 21:1--59, 2015. (WIAS Preprint 1692)- M. Thomas: Quasistatic damage evolution with spatial BV-regularization. DCDS-S 6:235--255, 2013, AIMS. (WIAS Preprint 1638)
- T. Roubíček, M. Thomas and C. Panagiotopoulos: Stress-driven local solution approach to quasistatic brittle delamination.
Nonlinear Analysis: Real World Applications 22(2015)645-663. (WIAS Preprint 1889)- A. Mielke, T. Roubíček and M. Thomas: From Damage to Delamination in Nonlinearly Elastic Materials at Small Strains,
J. of Elasticity, 109(2):235--273, 2012, Springer. (WIAS Preprint 1542)- P. Gruber, D. Knees, S. Nesenenko and M. Thomas: Analytical and numerical aspects of time-dependent models with internal variables, ZAMM Z. Angew. Math. Mech., 90 (2010) pp. 861--902. (WIAS Preprint 1460)
- M. Thomas and A. Mielke: Damage of nonlinearly elastic materials at small strain --- Existence and regularity results,
ZAMM Z. Angew. Math. Mech., 90 (2010) pp. 88--112. (WIAS Preprint 1397)- S. Bartels: Error control and adaptivity for a variational model problem defined on functions of bounded variation,
Math. Comp. 84(293):1217--1240,2015.- S. Bartels: Total variation minimization with finite elements: convergence and iterative solution,
SIAM J. Numer. Anal., 50(3):1162--1180, 2012.- S. Bartels: Broken Sobolev space iteration for total variation regularized problems.
IMA Journal of Numerical Analysis 36(2):493, 2016.- S. Bartels: Quasi-optimal error estimates for implicit discretizations of rate-independent evolutions,
SIAM J. Numer. Anal. 52(2), 708--716, 2014.- S. Bartels, A. Mielke, and T. Roubíček: Quasi-static small-strain plasticity in the limit of vanishing hardening and its numerical approximation, SIAM J. Numer. Anal., 50(2):951--976, 2012.
- S. Bartels, R. H. Nochetto, and A. J. Salgado: Discrete total variation flows without regularization,
SIAM J. Numer. Anal. 52(1), 363--385, 2014.- S. Bartels, R. H. Nochetto, and A. J. Salgado: A total variation diminishing interpolation operator and applications,
Math. Comp. to appear 2015, available online at http://aam.uni-freiburg.de/abtlg/ls/lsbartels/publ, 2013.
Last modified: 2018-01-23 by Marita Thomas