Quasilinear parabolic systems with discontinuous coefficients

[Next]:

Numerical simulation and optimization of SiC

[Up]:

Project descriptions

[Previous]:

Hysteresis phenomena

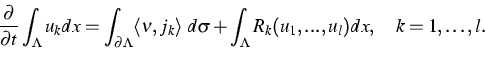
[Contents]

[Index]

Quasilinear parabolic systems with discontinuous coefficients and mixed boundary conditions on two-dimensional space domains

Collaborator: H.-Chr. Kaiser , H. Neidhardt , J. Rehberg

Supported by: DFG: ``Kopplung von van Roosbroeck- und Schrödinger-Poisson-Systemen mit Ladungsträgeraustausch'' (Coupling between van Roosbroeck and Schrödinger-Poisson systems including exchange of carriers)

Description:

The work of 2002 continued that reported in 2000; our aim was to prove a theorem on (local) existence for quasilinear parabolic systems on an L^p space which should enable the treatment of the van Roosbroeck system and similar reaction-diffusion systems in heterogeneous media in an L^p context. The motivation for this is the following: The natural formulation of balance laws is

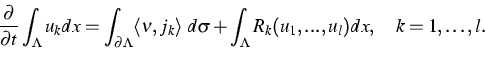$\begin{displaymath} \frac{\partial}{\partial t} \int_\Lambda u_k dx = \int_{\par... ...sigma + \int_{\Lambda} R_k(u_1,...,u_l) dx, \quad k=1,\ldots,l.\end{displaymath}$ (1)

Here u_k is the particle density of the k-th species, j_k is the corresponding flux, R_k a reaction term and $\Lambda$ any (suitable) subdomain of the whole domain under consideration. However, generally such equations are treated by substituting the boundary integral of the normal component of the current by the volume integral of the divergence of the corresponding current. The problem whether the thus obtained solutions in fact also satisfy the original equations remains completely unsolved. The mathematical reason is that in the calculi used up to now indicator functions of sets are not admissible as test functions. Hence, Gauss' theorem, which underlies the above-mentioned reformulation, is not applicable. Even worse, the notion of the normal component of the flux cannot be strictly defined when operating in negatively indexed Sobolev spaces. With the aim of coupling van Roosbrock's system with an open quantum system (describing nanosubstructures within the device under consideration) it is unavoidable to have the normal component of the current through interfaces at hand because current coupling is the most natural way to combine both systems (cf. [5]).

Apart from that, space discretization of such systems is often performed using finite volume schemes, cf. [4]. In order to compare such a scheme with the original equations these equations have to be valid in the space of integrable functions on the simulation domain.

Mathematically, the main results are as follows:

Theorem 1 Spatially two-dimensional quasilinear systems of the type

$\begin{displaymath} \frac {\partial {\bf w}}{\partial t} + \left( \begin{array}... ...a \mu_l \nabla w_l \end{array} \right )= {\bf f}(t,{\bf w}(t)),\end{displaymath}$ (2)

${\bf w}(T_0)={\bf w}_0$ ,admit exactly one (local) classical solution in a (suitably chosen) L^p space provided the data satisfy the following conditions:

1.: Each J_k maps a suitable interpolation space between the domain of $(-\nabla \mu_1 \nabla,..., -\nabla \mu_l \nabla)$ and $\bigl (L^p\bigr )^l$ into $L^\infty$ and additionally satisfies some continuity conditions.
2.: The mappings Z_1,1,...,Z_l,l take their values in a set of compact operators on L^p and also satisfy some continuity conditions.
3.: The coefficients $\mu_k$ may be discontinuous and the operators $-\nabla \mu_k \nabla$ are complemented by mixed boundary conditions.

This theorem rests heavily on classical results for abstract quasilinear parabolic equations in a Banach space [7], [10], interpolation results for function spaces which carry a trace condition on part of the boundary [2] and resolvent estimates for elliptic operators in divergence form including discontinuous coefficients and mixed boundary conditions [1].

Having the above theorem at hand, one succeeds in proving:

Theorem 2 The spatially two-dimensional van Roosbroeck system admits (locally in time) a classical solution in L^p. Hereby a broad class of recombination terms, including nonlocal ones, are admissible.

This theorem is derived from the first one by reformulating van Roosbroeck's system in a rather cumbersome procedure: One expresses the densities in terms of the electrostatic potential and the quasi-Fermi levels, then eliminates the time derivative of the electrostatic potential and afterwards the electrostatic potential itself via the nonlinear Poisson equation. This way, one ends up with a quasilinear system as above for the quasi-Fermi levels. The authors believe that the consistent treatment of the equations in much more regular spaces as before is not accidental but caused by the physical expectation that the quasi-Fermi levels should be the most regular objects within a heterogeneous context.

Finally, we will give a short outlook on the 3D case, which in our opinion should also be treated in a concept which provides as much regularity as possible (strong differentiability of the solution, the divergence of the currents being L^p functions....). The cornerstone to carry out the same program for the 3D case would be a result that the operators $\nabla \mu_k \nabla$ --including nonsmooth coefficients $\mu_k$ and mixed boundary conditions--provide isomorphisms between spaces $H^{1,q}_\Gamma$ , H^-1,q for a summability index q greater than 3. Unfortunately, this is known to be false in general (cf. [9]). In a forthcoming paper [8] it will be shown that it is true, however, in case of pure Dirichlet conditions and restrictions on the domain and the--discontinuous--coefficient functions. Further, it is expected that the same is true for smooth domains and the Laplace operator including mixed boundary conditions [3]. The task would be to prove that the latter assertion is really true, further to prove the analogous assertion in case of pure Neumann conditions and discontinuous coefficients and fit all these things together.

References:

J.A. GRIEPENTROG, H.-CHR. KAISER, J. REHBERG, Heat kernel and resolvent properties for second order elliptic differential operators with general boundary conditions on L^p, Adv. Math. Sci. Appl., 11 (2001), pp. 87-112.
J.A. GRIEPENTROG, K. GRÖGER, H.-CHR. KAISER, J. REHBERG, Interpolation for function spaces related to mixed boundary value problems, Math. Nachr., 241 (2002), pp. 110-120.
J. FREHSE, private communication.
H. GAJEWSKI, Analysis und Numerik von Ladungstransport in Halbleitern, GAMM-Mitteilungen, 16 (1993), pp. 35-57.
H.-CHR. KAISER, H. NEIDHARDT, J. REHBERG, Macroscopic current-induced boundary conditions for Schrödinger operators, to appear in: Integral Equations Operator Theory.
$\dito$ ,Classical solutions of quasilinear parabolic systems on two-dimensional domains, WIAS Preprint no. 765, 2002.
A. LUNARDI, Analytic Semigroups and Optimal Regularity in Parabolic Problems, Progr. in Nonlinear Differential Equations Appl., 16, Birkhäuser, Basel, 1995.
V. MAZ'YA, J. ELSCHNER, J. REHBERG, G. SCHMIDT, Solutions for nonsmooth quasilinear evolution systems, in preparation.
N.G. MEYERS, An L^p-estimate for the gradient of solutions of second order elliptic divergence equations, Ann. Scuola Norm. Sup. Pisa, 17 (1963), pp. 189-206.
P.E. SOBOLEVSKII, On equations of parabolic type in Banach spaces, Trudy Moskov. Mat. Obshch., 10 (1961), pp. 297-350.