Hysteresis phenomena

[Next]:

Quasilinear parabolic systems with discontinuous coefficients

[Up]:

Project descriptions

[Previous]:

Optimal control of surface heat treatments

[Contents]

[Index]

Hysteresis phenomena

Collaborator: Th. Jurke , O. Klein , J. Sprekels , D. Tiba

Cooperation with: P. Krejcí (Academy of Sciences of the Czech Republic, Prague), U. Stefanelli (Università di Pavia, Italy)

Supported by: DFG: ``Hysterese-Operatoren in Phasenfeld-Gleichungen'' (Hysteresis operators in phase-field equations)

Description:

To be able to deal with phase transitions, one has to take into account hysteretic phenomena that are modeled by hysteresis operators.

a) The modeling of uniaxial nonlinear thermo-visco-plastic developments leads to the system

	$\displaystyle{}\rho u_{tt} - \mu u_{xxt} = \sigma_x + f(x,t),$		(1)
	$\displaystyle{}\sigma = {\mathcal H}_1 [u_x,w] + \theta {\mathcal H}_2 [u_x,w],$		(2)
	$\displaystyle{}\left( C_V \theta + {\mathcal F} [u_x,w]\right)_t - \kappa \theta_{xx} = \mu u_{xt}^2 + \sigma u_{xt} + g(x,t,\theta),$		(3)
	$\displaystyle{}\nu w_t + {\mathcal H}_3[u_x,w] + \theta {\mathcal H}_4[u_x,w] = 0,$		(4)

where u, $\theta$ , $\sigma$ , and w are the unknowns displacement, absolute temperature, elastoplastic stress, and freezing index, respectively, $\rho$ , $\mu$ , C_V, and $\nu$ are positive constants, f, g are given functions, and ${\mathcal H}_1, \dots, {\mathcal H}_4$ , and ${\mathcal F}$ are hysteresis operators. In [4], this system has been derived, its thermodynamic consistency has been proved, and the existence of a unique strong solution to an initial-boundary value problem for this system has been shown. In [1], this existence result has been generalized to the case of a more general boundary condition for u and a weaker assumption for ${\mathcal H}_2$ and ${\mathcal H}_4$ . More precisely, the assumption that these operators are bounded has been replaced by the assumption that the clockwise admissible potential connected to these operators can be bounded from below by $- C {\mathcal F}$ ,with some positive constant C.

A large-time asymptotic result for this system has been derived in [2]. An approach used therein to derive uniform estimates for the solutions to partial differential equations involving hysteresis operators has been further investigated in [3], leading to the notion of ``outward pointing hysteresis operators''. Moreover, in [3], generalizations of scalar Prandtl-Ishlinskii operators have been introduced and investigated with respect to their thermodynamic consistency.

b) In [5], a control problem for an ordinary differential system with hysteresis has been investigated. For controls $u : [0,T] \to \IR^m$ ,one considers the system

z'	=	$\displaystyle{}f(t,z,y,u), \quad \text{in} \quad [0,T], \quad z(0) = z_0 \in \IR^m,$	(5)
y(t)	=	$\displaystyle{}{\mathcal W}\,(g\circ z)(t) \qquad \text{in} \quad [0,T]$	(6)

with $f : [0,T] \times \IR^N \times \IR \times \IR^m \to \IR^N$ and $g : \IR^N \to \IR$ being continuous functions, and $\mathcal W : C[0,T] \to C[0,T]$ being a hysteresis operator. Under appropriate conditions, the existence of at least one global solution has been proved. Moreover, $u(t) \in U$ for all $t\in [0,T]$ , for a bounded, closed, convex set $U \subset \IR^m$ . For such controls u and the corresponding solutions (z, y) to (5), (6) we associate the cost functional

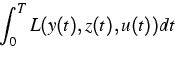$\begin{displaymath} \int_0^T L(y(t),z(t),u(t)) dt\end{displaymath}$

(7)

with $L : \IR \times \IR^N \times U$ continuous in y, z, convex and lower semicontinuous with respect to u. It has been proved that the corresponding optimal control problem has at least one solution.

An approximation method and a conceptual algorithm are discussed as well.

References:

TH. JURKE, O. KLEIN, Existence results for a phase-field model in one-dimensional thermo-visco-plasticity involving unbounded hysteresis operators, in preparation.
O. KLEIN, Asymptotic behaviour for a phase-field model with hysteresis in one-dimensional thermo-visco-plasticity, WIAS Preprint no. 734, 2002, submitted.
O. KLEIN, P. KREJCI, Outwards pointing hysteresis operators and asymptotic behaviour of evolution equations, WIAS Preprint no. 748, 2002, Nonlinear Anal. TMA, in print.
P. KREJCI, J. SPREKELS, U. STEFANELLI, Phase-field models with hysteresis in one-dimensional thermo-visco-plasticity, WIAS Preprint no. 655, 2001, submitted.
J. SPREKELS, D. TIBA, Optimization of ordinary differential systems with hysteresis, WIAS Preprint no. 747, 2002, submitted.