|
|
|
|
[Contents] | [Index] |
Collaborator: O. Klein , P. Philip , J. Schefter , J. Sprekels
Cooperation with: Ch. Meyer, A. Rösch, F. Tröltzsch (Technische Universität Berlin) , K. Böttcher, D. Schulz, D. Siche (Institut für Kristallzüchtung (IKZ), Berlin)
Supported by: BMBF: ``Numerische Simulation und Optimierung der Züchtung von SiC-Einkristallen durch Sublimation aus der Gasphase'' (Numerical simulation and optimization of SiC single crystal growth by sublimation from the gas phase);
DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien'' (Research Center ``Mathematics for Key Technologies'')
Owing to numerous technical applications in electronic and optoelectronic devices, such as lasers, diodes, and sensors, the industrial demand for high quality silicon carbide (SiC) bulk single crystals remains large. It is still a challenging problem to grow sufficiently large SiC crystals with a low defect rate. Sublimation growth of SiC bulk single crystals via physical vapor transport (PVT), also known as the modified Lely method, has been one of the most successful and most widely used growth techniques of recent years. It is the goal of this project to use mathematical modeling and numerical simulation to help optimizing the PVT method.
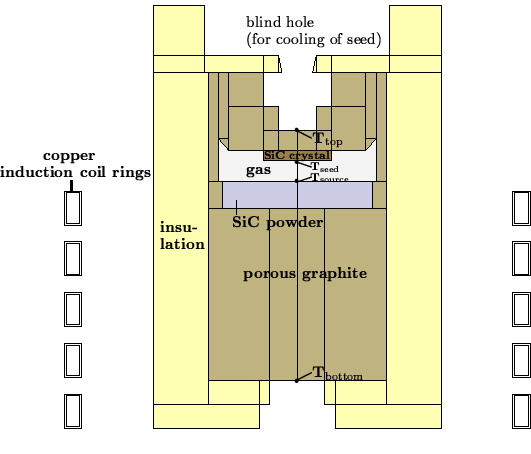
During PVT, a graphite crucible (see Figure 1) is placed in a low-pressure inert gas atmosphere consisting of argon. The crucible is then intensely heated, e.g., by induction heating, to temperatures up to 3000 K. Inside the crucible, polycrystalline SiC source powder sublimates, adding molecules made up of silicon and carbon to the gas phase. For the moment, we abuse notation to denote the total of the added species as the SiC gas, notwithstanding the fact that it consists predominantly of other molecules than SiC. The SiC gas diffuses through the cavity from the powder to the SiC seed. As the single crystalline seed is kept at a temperature below that of the SiC source, SiC gas crystallizes on the seed, which thereby grows into the reactor.

|
The physical and mathematical modeling of the growth process leads to a highly nonlinear system of coupled partial differential equations. In addition to the kinetics of a rare gas mixture at high temperatures, one has to consider heat transport by conduction and radiation, reactive matter transport through porous and granular media, and different kinds of chemical reactions and phase transitions. Moreover, several free boundaries occur in the model, e.g., due to the growing crystal and due to the sublimating source powder. The main control parameters with respect to an optimization of the crystal growth process are the design of the growth apparatus, the position of the induction coil, the heating power, and the inert gas pressure.
Within the research year 2002,
the conditions for the growth of the crystal have been further investigated.
As a first approximation, one can assume that
the pressure ![]() of the SiC gas
at the surface of the crystal is identical to the
corresponding equilibrium pressure
of the SiC gas
at the surface of the crystal is identical to the
corresponding equilibrium pressure ![]() .
At the powder surface, one would then make the corresponding
assumption. However, this approach supposes that
the growth process is limited by the transport
through the gas phase and it omits the influence of the growth kinetics.
.
At the powder surface, one would then make the corresponding
assumption. However, this approach supposes that
the growth process is limited by the transport
through the gas phase and it omits the influence of the growth kinetics.
To take into account the influence of the growth kinetics,
one can use a Hertz-Knudsen formula to determine the mass flux
from the gas to the crystal:
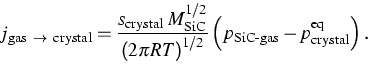 |
(1) |
If the model is to include the observed graphitization of the powder
source, it becomes necessary to consider the different constituents of
the ``SiC gas'', consisting of Si, ![]() ,
,
![]() ,
,
![]() , SiC, etc. Instead of simple sublimation, one has to
consider several chemical reactions occurring at the surfaces.
Then, instead of equilibrium pressures for the different
components, one merely has relations between the different
partial pressures in the equilibrium, resulting from
the mass action laws of the considered chemical reactions.
For example, from the reactions
, SiC, etc. Instead of simple sublimation, one has to
consider several chemical reactions occurring at the surfaces.
Then, instead of equilibrium pressures for the different
components, one merely has relations between the different
partial pressures in the equilibrium, resulting from
the mass action laws of the considered chemical reactions.
For example, from the reactions
![]()
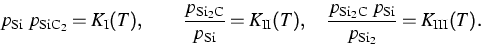
Further research is ongoing to formulate the corresponding mass action laws for reactions changing the composition of the surface, to model the kinetics of the chemical reactions, and to determine the involved material parameters.
The heat sources caused by induction heating are computed via an axisymmetric complex-valued magnetic scalar potential that is determined as the solution of an elliptic PDE using the imposed voltage as input data. The scalar potential enables one to calculate the resulting current density and thus the heat sources [2, 3, 4].
The transient nonlinear and nonlocal heat transport equations are
discretized using an implicit Euler scheme in time and a finite volume
method in space. Within the period covered by this report, existence
and uniqueness results for the solution to the resulting
nonlinear and nonlocal discrete scheme
have been established. Moreover, discrete ![]() -L1 a priori
estimates have been proved [6].
-L1 a priori
estimates have been proved [6].
Within the covered research period, the simulation software
WIAS-HiTNIHS (see page ![]() )
has been installed at
the IKZ. Figure 2 depicts results of a
numerical simulation of the heating process for the configuration of
Figure 1 which we published in [5].
The angular frequency used for the induction heating is
)
has been installed at
the IKZ. Figure 2 depicts results of a
numerical simulation of the heating process for the configuration of
Figure 1 which we published in [5].
The angular frequency used for the induction heating is
![]() , where f=10 kHz. The average
total power P is prescribed according to the following linear ramp:
, where f=10 kHz. The average
total power P is prescribed according to the following linear ramp:
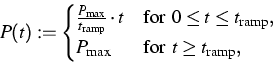 |
(2) |
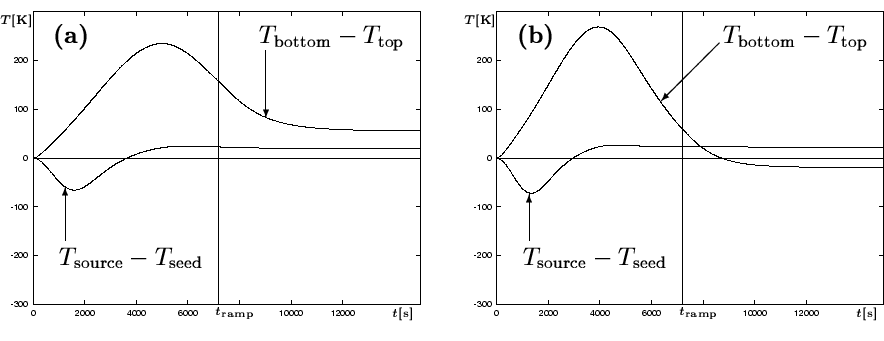
|
We investigate the
relation between the temperature differences
![]() and
and
![]() . The relation between
. The relation between
![]() and
and
![]() is of importance,
as in physical growth experiments
is of importance,
as in physical growth experiments ![]() and
and
![]() are measured, and
are measured, and ![]() is often used as an indicator for
is often used as an indicator for
![]() which is not accessible to direct
measurements, but crucial for the growth process.
Figure 2 shows that in
both cases,
which is not accessible to direct
measurements, but crucial for the growth process.
Figure 2 shows that in
both cases, ![]() is no
indicator for
is no
indicator for ![]() before
before ![]() has reached its
quasi-stationary final state, but, more
importantly, even in the stationary state at growth temperature,
has reached its
quasi-stationary final state, but, more
importantly, even in the stationary state at growth temperature,
![]() is almost three times as large as
is almost three times as large as
![]() for
for ![]() , and
, and
![]() and
and ![]() have different signs
for
have different signs
for ![]() .The numerical experiments show that for the considered configuration,
there is generally no easy relation between
.The numerical experiments show that for the considered configuration,
there is generally no easy relation between ![]() and
and ![]() .Even though there might be configurations where the situation is
better, for each real growth system, the validity of using
.Even though there might be configurations where the situation is
better, for each real growth system, the validity of using ![]() as an indicator for
as an indicator for ![]() needs to be
verified by some other method (e.g., numerical simulation).
needs to be
verified by some other method (e.g., numerical simulation).
References:
|
|
|
[Contents] | [Index] |