Phasenfeldgleichungen und Stefan-Probleme

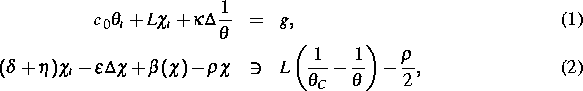
Bearbeiter: O. Klein, J. Sprekels  

Kooperation: P. Colli, Universität Turin,

M. Grasselli, Polytechnikum Mailand

Beschreibung der Forschungsarbeit:

In Fortführung der Untersuchungen vom Vorjahr wurden Phasenfeldgleichungen vom Penrose-Fife-Typ und Stefan-Probleme untersucht, mit denen diffusive Phasenübergänge modelliert werden. Neben der numerischen Implementation der im Vorjahr (siehe [5]) hergeleiteten Semidiskretisierung der Phasenfeldgleichungen wurden neue Existenzresultate bewiesen. So konnte unter anderem gezeigt werden (siehe [6]), daß eine Anfangsrandwertaufgabe für ein Penrose-Fife-System der Form

wobei 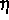eine vom Ort abhängige Funktion ist, eine Lösung hat, die mit Hilfe der Semidiskretisierung approximiert werden kann. Das System (1), (2), vervollständigt mit geeigneten Anfangs- und Randbedingungen, stellt ein vereinfachtes Modell zum anisotropen Kristallwachstum dar.

Die numerische Implementation der Semidiskretisierung baut auf KASKADE, einer am ZIB entwickelten Toolbox für adaptive Multilevelmethoden, auf. Die Semidiskretisierung in [5] führt in jedem Zeitschritt auf ein System nichtlinearer elliptischer Gleichungen. Zur näherungsweisen Lösung dieses Systems wurde, siehe [6], ein Ansatz übertragen, der für bestimmte nichtlineare skalare elliptische Gleichungen von Kornhuber in [7, 8] beschrieben wurde. Mit einer geeigneten Wahl für die Funktion konnte dendritisches Wachstum simuliert werden (siehe Abbildung 1). Mit Unterstützung von G. Reinhardt (Forschungsgruppe Numerische Mathematik und Wissenschaftliches Rechnen) wurden die numerischen Resultate in Form eines Videos visualisiert.

Weiterhin wurden Stefan-Probleme (siehe [1]) und Phasenfeldgleichungen untersucht, die sich für Materialien mit thermischer Erinnerung ergeben. So konnte in [2] gezeigt werden, daß Anfangsrandwertaufgaben für Penrose-Fife-Systeme der Form

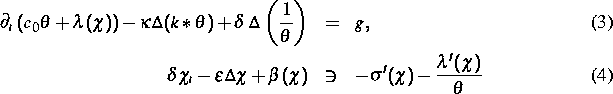
unter schwachen Voraussetzungen an 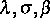und den Memory-Kern k eine eindeutig bestimmte (schwache) Lösung besitzen. Durch dieses Resultat sind erstmalig diffusive Phasenübergänge in einer weiten Klasse von Materialien mit thermischer Erinnerung der mathematischen Behandlung zugänglich gemacht worden.

Das Thema wurde im Rahmen des EU-Projektes ,,Phase Transitions and Surface Tension`` bearbeitet.

Projektliteratur:

1.   P. COLLI, M. GRASSELLI, J. SPREKELS, Automatic control via thermostats of a hyperbolic Stefan problem with memory, WIAS-Preprint No. 282, Berlin 1996, eingereicht.

2.   P. COLLI, J. SPREKELS, Weak solution to some Penrose--Fife phase-field systems with temperature-dependent memory, WIAS-Preprint No. 290, Berlin 1996, eingereicht.
3.  

   , On a Penrose-Fife model with zero interfacial energy leading to a phase-field system of relaxed Stefan type, Ann. Mat. Pura Appl. , CLXIX (1995), pp. 269--289.

4.  

   , Stefan problems and the Penrose-Fife phase field model, WIAS-Preprint No. 127, Berlin 1994, erscheint in: Adv. Math. Sci. Appl.

5.   O. KLEIN, A semidiscrete scheme for a Penrose-Fife system and some Stefan problems in , Adv. Math. Sci. Appl., Vol. 7, No. 1 (1997), pp. 489--521.

6.  

   , Some approximation results for phase-field systems of Penrose-Fife type and Stefan problems, Dissertation, in Vorbereitung.

7.   R. KORNHUBER, Adaptive monotone multigrid methods for some non-smooth optimization problems , WIAS-Preprint No. 156, Berlin 1995.

8.   , Adaptive monotone multigrid methods for nonlinear variational problems, erscheint 1997 in: Advances in Numerical Mathematics, John Wiley & Sons and B. G. Teubner.

9.   O. PENROSE, P. C. FIFE, Thermodynamically consistent models of phase-field type for the kinetics of phase transitons. Physica D, 43 (1990), pp. 44--62.