DFG-Forschungszentrum Matheon Berlin - TU Berlin - WIAS

Project C10: Modelling, Asymptotic Analysis and Numerical Simulation
of Interface Dynamics on the Nanoscale

[PROJECT DATA]
Project head: Prof. Dr. Barbara Wagner , TU Berlin/WIAS. 
Support: Matheon, DFG, Research Center
Research Team: Dr. Dirk Peschka, WIAS (since June 2010) and
Dr. Maciek Korzec, TU Berlin (August 2006-April 2011 at WIAS, now TU Berlin) 
Former Project Members: PD Dr. Andreas Münch co-head of the project until September 2008; HU Berlin; now at the Mathematical Insitute, Oxford, U.K.
Dr. Peter Evans, HU Berlin until May 2010, now at German Research Center for Geosciences, Potsdam
Publications: see below
Contact: For further information about this project, please contact Prof. Dr. Barbara Wagner.
nanoscale heterostructures produced by epitaxy rim formed in a slipping thin liquid film

Background

Liquid or solid thin films are ubiquitous in nature and technology. They are typically used as coatings to define the functionality of surfaces. The dynamics and morphology during production depend, apart from their material properties, largely on properties of the interfaces they make with e.g. a rigid or deformable substrate and the surrounding air or gas. When the thickness of the thin films are in micro- or nanometer scale the conditions at the interfaces play the dominant role in the morphological evolution during production of the film.

Apart from intermolecular and capillary forces, for liquid films, the wetting or dewetting dynamics may e.g. be controlled by interfacial slip. For solid films, apart from surface diffusion and elastic properties, substrate-film crystal lattice mismatch and elastic anisotropy have a major impact on self-organization of nanostructures during processess such as epitaxial growth or solid phase "dewetting".

Even though the underlying mathematical models that describe these processes are very different for liquid and solid films, what unifies our approach results from the scale separation of the thickness of the film to the lateral morphological scales, the ratio of which is generally small. In the asymptotic limit of the small scale ratio a reduction of the free boundary problems to thin film equations for the interfaces can be achieved. The resulting nonlinear partial differential equations are typically of high (4th or 6th) order, of parabolic type and often degenerate at the three-phase contact line of the evolving nanostructures.

The derivation of such model equations has significant advantages, where mathematical investigations only deal with equations for the interface profile which live on a dimension-reduced space. As a result large-scale and long-time numerical simulation of the underlying 3D free-boundary problems are possible and needed for comparison with experimental results of our collaborators in the applied fields and industry.

Apart from developing mathematical models that arise in various thin-film coating and growth proceses, a focus of this project is also the mathematical analysis and numerical simulation of these high-order partial differential equations.

In the past we have investigeted problems that concern thin-(liquid)-film problems that include effects of gravity, Marangoni shear stresses and intermolecular forces or non-Newtonian rheology. The interplay of these effects leads to rich phenomena, which include nonlinear wave motion such as new types of nonclassical shock waves, pinch-off and hole formation, or pattern formation such as the fingering at the front of a driven liquid film [Mue03], [ESR04], [MW04], [JAM05], [ME05], [AMW08], [AMW07]. The development of thin film models that take account of various orders of magnitude of interfacial slip could successfully explain a number of nanofluidic effects observed in experiments and resulted in a number of significant contributions in Nanofluidics, [FMWRJ07], [FJMWW05], [MWW05], [RMWB05], [BMRW06], [KMW09] and more, see publication list. Moreover, our expertiese lead to additional industrial funding for the development of new models and numerical software for roll coating processes.

Concepts and methodologies from our invesitgations in liquid films were also used to develop dimension-reduced thin film models, of Cahn-Hilliard type, for the epitaxial growth of crystal layers (such as Germanium) on top of a crystal surface (e.g. silicon). The susceptability of such systems to morphological instabilities, most notably of Asaro-Tiller-Grinfeld type, leads to the self-assembly of so-called quantum dots. In our dimension-reduced models we are able to follow the long-time dynamics such as coarsening effects for large arrays of quantum dots, which represents the groundwork for applications for the design of superlattices of quantum dots, having defined optoelectronic properties, see e.g. [KEMW08], [KE10], [K10].

Current Research

The key aspects of the project are

Dynamics of thin-solid film growth

On the more theoretical side we have been extending further fundamental aspects such as existence results or long-time dynamics of high-order nonlinear PDEs (collaboration with Piotr Rybka, Warsaw University). For a sixth order Cahn-Hilliard type equation that describes the faceting of a growing surface, results have already been established. For the 1+1D problem a Galerkin approach has been used to prove the global existence and uniqueness of solutions [KE10], while the same result has been obtained for the 2+1D problem with a completely different method, a fix-point approach, Fourier-expansions and semi-group theory [KR10,KRN10]. Further cooperation with the analysis of the omega-limit sets of related equations are in progress.

Regarding modeling aspects of thin crystalline growth, we have reviewed certain classes of surface energy formulations that have been used in the literature and by us. We show in [KMW11] that certain symmetry properties in these mathematical descriptions of the physical processes are equivalent. The understanding and the ability to deal with complicated (highly nonlinear) expressions for the surface energy is crucial when it comes to applications for realistic set-ups. As a result of our investigations we obtained a highly complex description for the anisotropic surface energies and corresponding sixth order partial differential equation that captures the self-assembly of strongly anisotropic patterns. We have formulated and implemented different time-stepping schemes for our Fourier collocation method to find an optimal algorithm in terms of stability and accuracy. The numerical results show how coarsening can be slowed down dramatically when the anisotropy is strong.

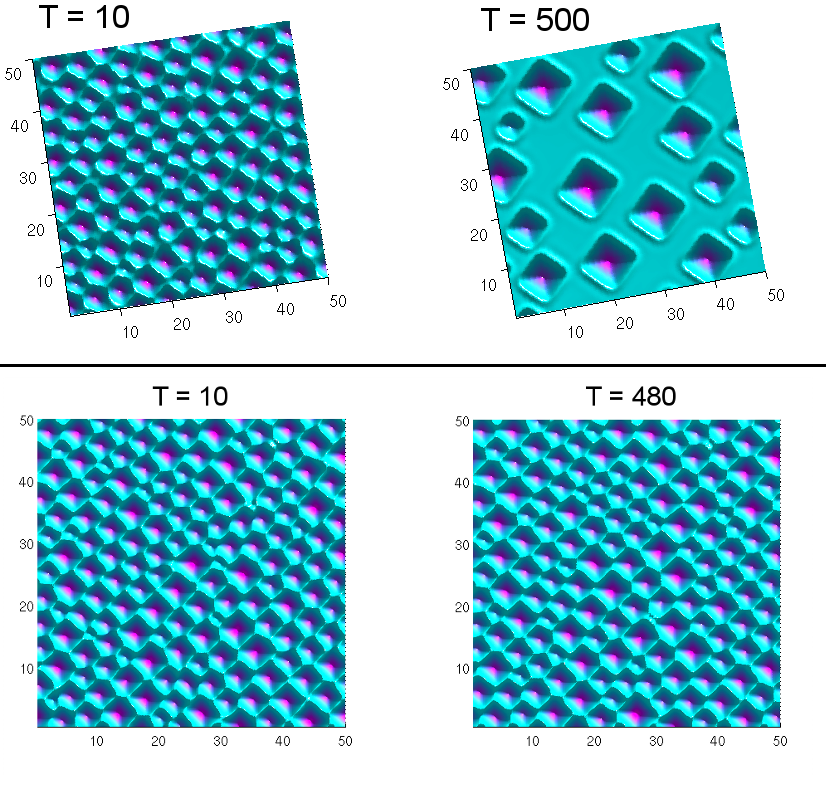
Figure 1: Slow down of the coarsening by increasing the anisotropy from (top G=0.5) to (bottom G=1) in numerical simulation [KMW11] Figure 2: An example of our numerical simulation of stacked quantum dots in 2-D for different spacer thicknesses shows that anti-correlated stacking is observed for the smallest value of the spacer thickness.
Our numerical simulations are based on a pseudospectral method, where we use a third order semi-implicit backward differentiation formula (SBDF) time-stepping procedure and an exponential time-differencing (ETD) method with a fourth order Runge-Kutta (RK4) time-integration.

One of our goals was to use our models and numerical schemes for applications in the designs for 3rd generation solar cell such as stacked layers of quantum dots. For such systems we extended our previously derived models [KE10,KMW11] with a new elasticity term that arises from a buried layer of quantum dots. For small mismatch between film and substrate linear elasticity was used. We then derived a reduced expression for the strain energy density evaluated on top of the surface taking account of the buried dots. The problem greatly simplifies if instead appropriate boundary conditions, that optimally reflect the buried nanostructures are constructed. In this way the energy landscape can be altered such that correlations between successive layers are possible.

Continuum models with microstructure

Our past investigations of dewetting of thin films of liquid polymer or polymer solutions from hydrophobic substrates has shown that interfacial slip may dominate the dynamics and morphology of the film. In the meantime our thin film models have been validated experimentally in many publications [FJMWW05]. In addition existence of weak solutions for the new thin film models has been established [KLN12].From the modeling aspects and to better understand the dynamics of polymers in confinement, one focus of this project was to understand the microscopic origins of effective quantities such as slip. The problem is how to incorporate the underlying nonuniform distribution and dynamics of the polymer chains. We basically followed two main appoaches for appropriate mathematical models in a continuum framework. One was to look at a simple problem of a thin film, consisting of tiny objects (e.g. particles) immersed in a Newtonian liquid undergoing shear. For this simple situation a new model has been developed by Bertozzi (UCLA), Murisic (Princeton U.) and Pausader (Courant Institute) and Peschka. That model describes the transport of the volumetric particle density and its interaction with the flow including shear induced migration. For that model a lubrication approximation was applied and for the resulting system of hyperbolic conservation laws numeric and asymptotic solutions were compared with experiments and good agreement was found [MPPB12].

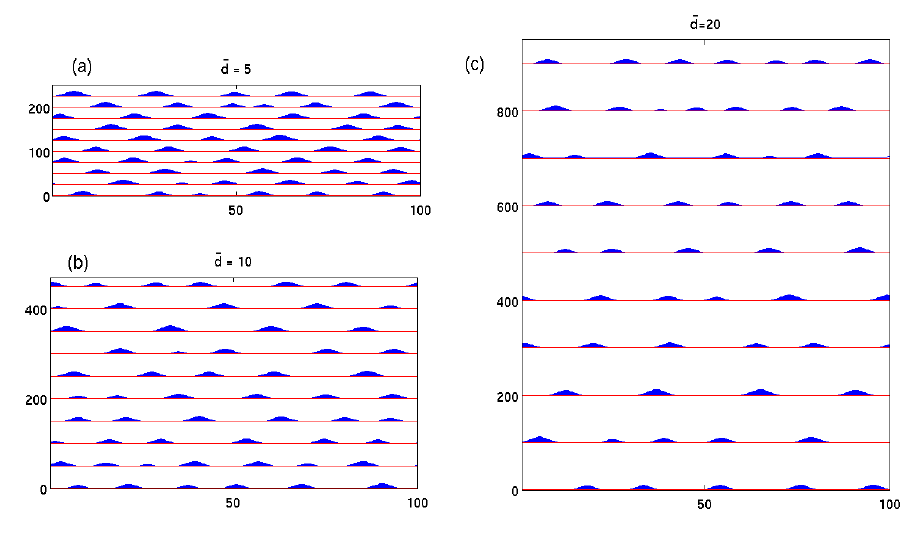
Figure 3: Motion of suspension flow fronts (particles and liquid) on an incline with different inclination angles (left 10deg, right 20deg) and comparison of experiment (symbols) with theory (lines) shows good agreement [MPPB12]
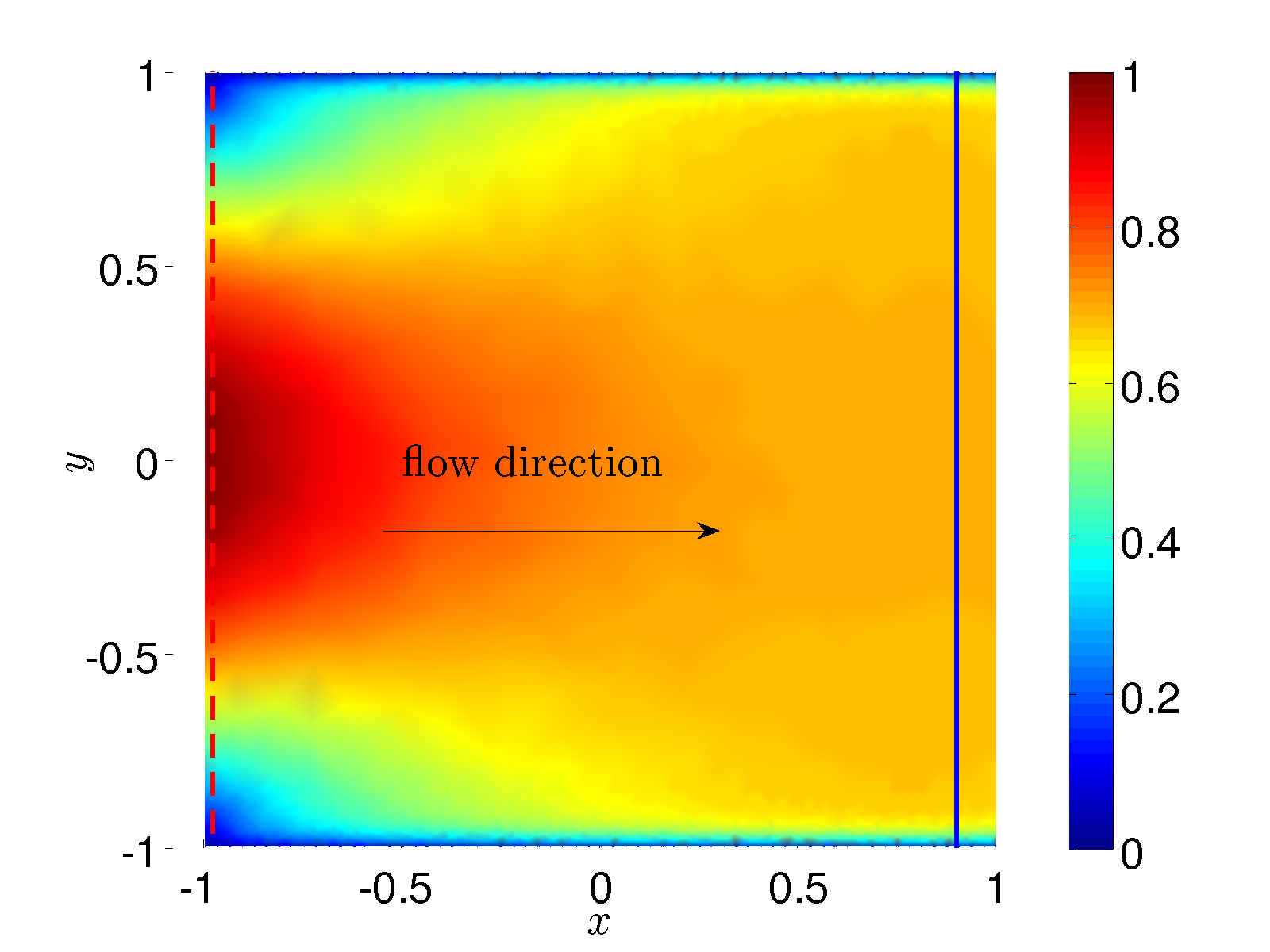
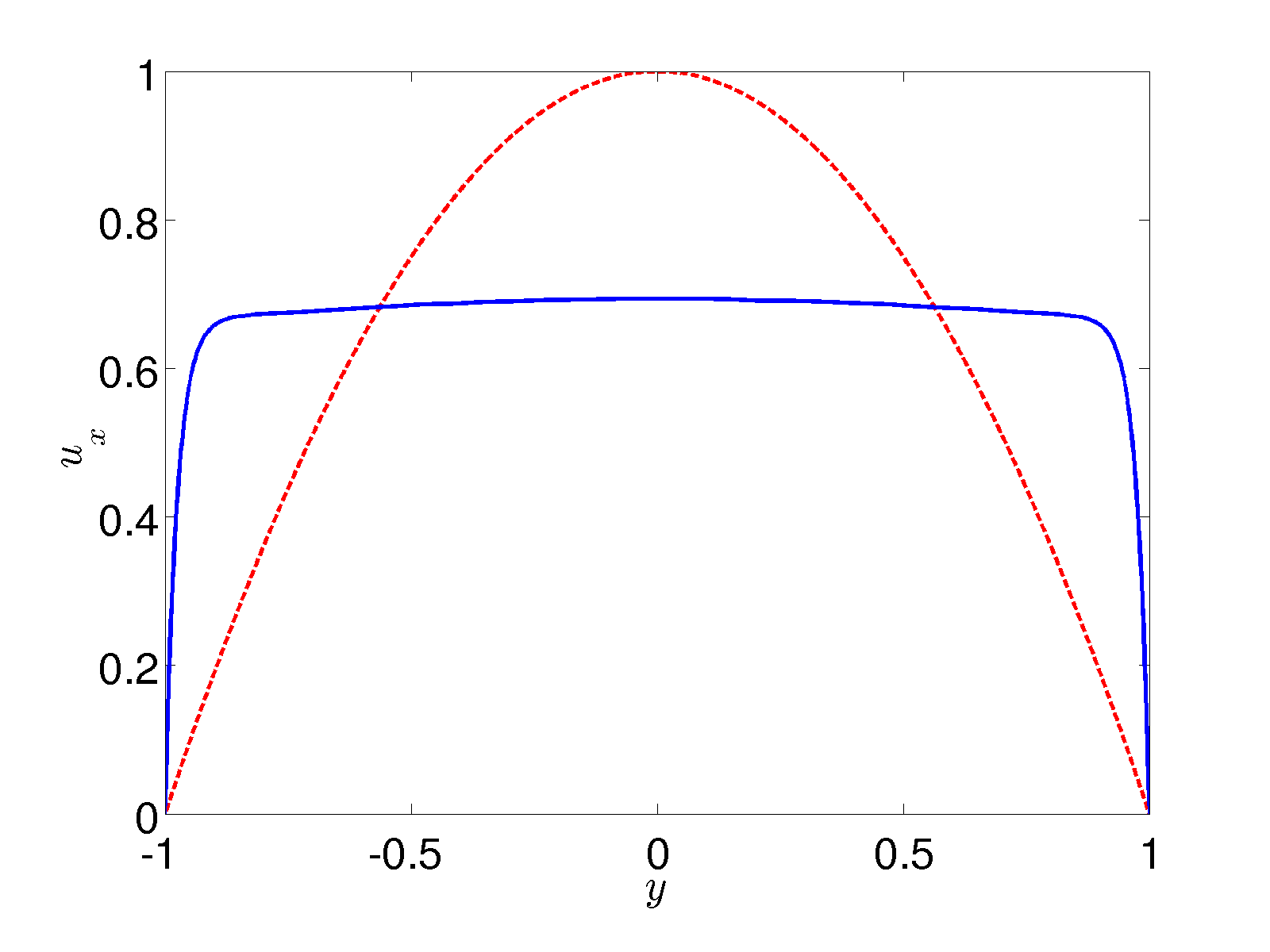
The other approach is to consider novel rheological models that incoporate spatially nonuniform stress distributions evolving in time. At first we neglect the coupling to the evolution equation for the concentration of the microscopic objects (particle, polymer chains). In collaboration with Cook and Braun (U. Delaware) we considered only the simplest case of an upper-convected Maxwell fluid allowing in addition for stress diffusion. Surprisingly, we found that already this simple model produces boundary layers in a shearing flow from which we derived an effective Navier-slip condition. Moreover, we derived sharp-interface models that correspond to lubrication models we found previously.
Figure 4: Flow from an upper-convected Maxwell model with parabolic inflow at x=-1. Behind the inflow a boundary layer forms and the velocity profile can be described with an effective Navier-slip condition. Figure 5: cross section through the velocity profile in Figure 4 at x=0.9 (blue full line) compared to the inflow (red dashed line) shows a significant boundary layer.

Impact

Further applications of our work in C10 were undertaken within the recently established ``Ausbau PVcomB''. In a collaboration with the Helmholtz Center Berlin (HZB) we investigate the solid phase ``dewetting'' of silicon layers on silicon dioxide surfaces.

We have developed finite element toolbox in MATLAB, suited for the simulation of flows of viscous liquids with a complex rheology and also with free capillary boundaries. At the moment we have implementations of the Navier-Stokes equations and coupling to upper-convected Maxwell fluid equations, Cahn-Hilliard equations with non-constant mobility, Stokes equation coupled to Nernst-Planck-Poisson (or general convection-diffusion problems) equations. We use our software to numerically investigate a model we have developed for electrorheological/-chemical flow of nonpolar liquids coupled to equations for discrete particles. The industry-funded research is in collaboration with the groups of Peukert and Baensch (University Erlangen) supplying experimental and numerical support.
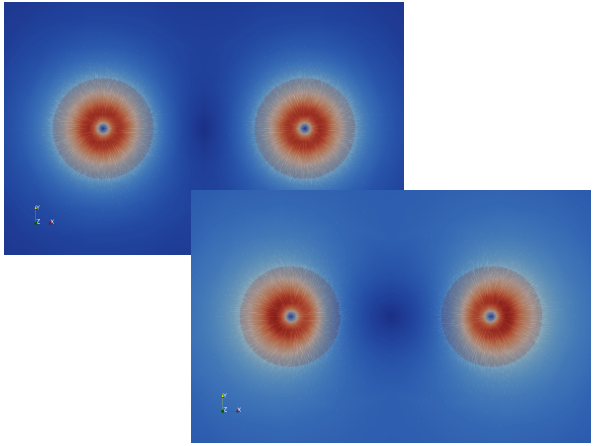Figure 6: Charged particles are shielded in a charged liquid (top=with charge, bottom=without charge)

Collaboration and partners

Publications

NOTE: Articles posted on this page are subject to copyright restrictions. They may be downloaded for personal use only. Any other use requires prior permission of the authors and the relevant publishers.

Matheon third funding round (since June 2010)

Theses

[K10] M. D. Korzec.
Continuum modeling, analysis and simulation of the self-assembly of thin crystalline films.
Ph.D. thesis, TU Berlin 		PDF ABS

Submitted articles

[KMW11] M. D. Korzec, A. Münch and B.  Wagner.
Anisotropic surface energy formulations and their effect on stability of a growing thin film.
submitted (also: Matheon preprint number 839 (2012).) 		PDF
[MPPB12] N. Murisic, B. Pausader, D. Peschka, A. L. Bertozzi.
Dynamics of particle settling and resuspension in viscous liquids.
submitted (Also WIAS preprint number 1679, (2012); Matheon preprint number 865, (2012)) 		PDF
[KRW12] G. Kitavtsev, L. Recke and B. Wagner.
Asymptotics for the spectrum of a thin film equation in a singular limit.
submitted (Also WIAS preprint number 1555, (2011)) 		PDF
[KRN10] M. D. Korzec, P. Rybka and P. Nayar.
Global weak solutions to a sixth order Cahn-Hilliard type equation.
submitted (Also WIAS preprint number 1581.) 		PDF

Papers published or accepted in peer-reviewed journals

[KW11] G. Kitavtsev and B. Wagner.
Coarsening dynamics of slipping droplets.
J. Engin. Math., 66:271-292, 2010. (Also WIAS preprint number 1381.) 		PDF
[KR10] M. D. Korzec and P. Rybka.
On a higher order convective Cahn-Hilliard type equation.
(accepted for publication in SIAP) (Also WIAS preprint number 1582.) 		PDF
[KRW11] G. Kitavtsev, L. Recke and B. Wagner.
Centre manifold reduction approach for the lubrication equation.
Nonlinearity, 34:2347-2369, 2011. (Also WIAS preprint number 1554.) 		PDF
[KPMWHS11] K. Kostorou, D. Peschka, A. Münch, B. Wagner, S. Herminghaus and R. Seemann.
Interface morphologies in liquid/liquid dewetting.
Chemical Engineering and Processing: Process Intensification, 50:531-536, 2011. (Also WIAS preprint number 1560.) 		PDF
[MW11] A. Münch and B. Wagner.
Impact of slippage on the morphology and stability of a dewetting rim.
Journal of Physics: Condensed Matter, 23:184101, 2011. (Also WIAS preprint number 1556.) 		PDF
[MPW11] A. Münch, C. P. Please and B. Wagner.
Spin coating of an evaporating polymer solution.
Physics of Fluids, 23:1021101, 2011.(Also WIAS preprint number 1558.) 		PDF
[KMN10] D. Peschka, A. Münch and B. Niethammer.
Self-similar rupture of viscous thin films in the strong-slip regime.
Nonlinearity, 23, 2010.(Also WIAS preprint number 1418.) 		PDF
[KE10] M. D. Korzec and P. L. Evans.
From bell shapes to pyramids: A reduced continuum model for self-assembled quantum dot growth.
Physica D, 239(8): 465-474, 2010. Matheon preprint #583. (Also WIAS preprint number 1434.) 		PDF ABS

Proceedings

[K11] M. D. Korzec.
The effect of deposition in a model for quantum dot self-arrangement.
PAMM, Proc. of GAMM 2011, 397.398, 2011. 		PDF

Matheon second funding round (2006-May 1010)

Papers published or accepted in peer-reviewed journals

[AMW07] K. Afanasiev, A. Münch, and B. Wagner.
On the Landau-Levich problem for non-Newtonian liquids.
Phys. Rev. E, 76:036307, 2007. (Also WIAS preprint number 1215.) 		PDF ABS
[AMW08] K. Afanasiev, A. Münch, and B. Wagner.
Thin film dynamics on vertically rotating disks.
Applied Mathematical Modelling, 32:1894-1911, 2008. (Also WIAS preprint number 1074.) 		PDF ABS
[BMRW06] R. Blossey, A. Münch, M. Rauscher and B. Wagner.
Slip vs. viscoelasticity in dewetting thin films.
European Phys. J. E - Soft Matter, 20(3): 267-271, 2006. (Also WIAS preprint number 1192.) 		PDF ABS
[DW05] W. Dreyer and B. Wagner.
Sharp-interface model for eutectic alloys. Part I: Concentration dependent surface tension.
Interfaces and Free Boundaries, 7(2):199-227, 2005. (Also WIAS preprint number 885.) 		PDF ABS
[EKM06] P. L. Evans, J. R. King, and A. Münch.
Intermediate-asymptotic structure of a dewetting rim with strong slip.
AMRX Appl. Math. Res. Express, vol. 2006, Article ID 25262, 2006. 		PDF ABS
[EM06] P. L. Evans and A. Münch.
Interaction of advancing fronts and meniscus profiles formed by surface-tension-gradient-driven liquid films.
SIAM J. Appl. Math., 66(5):1610-1631, 2006. 		PDF ABS
[FMWRJ07] R. Fetzer, A. Münch, B. Wagner, M. Rauscher and K. Jacobs.
Quantifying hydrodynamic slip: A comprehensive analysis of dewetting profiles.
Langmuir, 23(21):10559-10566, 2007. 		PDF ABS
[FRMWJ06] R. Fetzer, M. Rauscher, A. Münch, B. Wagner, and K. Jacobs.
Slip-controlled thin film dynamics.
Europhys. Lett., 75(4):638-644, 2006. 		PDF ABS
[KMW09] J. King, A. Münch, and B. Wagner.
Linear stability analysis of a sharp-interface model for dewetting thin films.
J. Engrg. Math., 63:177-195, 2009. (Also WIAS preprint number 1248.) 		PDF
[KMW06] J. R. King, A. Münch, and B. Wagner.
Linear stability of a ridge.
Nonlinearity, 19:2813-2831, 2006. (Also WIAS preprint number 1070.) 		PDF ABS
[KW09] G. Kitavtsev and B. Wagner.
Coarsening dynamics of slipping droplets.
J. Engrg. Math., , 2009. (Also WIAS preprint number 1381.) 		PDF ABS
[KEMW08] M. D. Korzec, P. L. Evans, A. Münch, and B. Wagner.
Stationary solutions of driven fourth- and sixth-order Cahn-Hilliard type equations.
SIAM J. Appl. Math., 69(2):348-374, 2008.
Preprint arXiv:0712.2482v1 [math-ph] available at http://arxiv.org/abs/0712.2482		 PDF ABS
[MW08] A. Münch and B Wagner.
Galerkin method for feedback controlled Rayleigh-Benard convection.
Nonlinearity, 21:2625-2651, 2009. (Also WIAS preprint number 907.) 		PDF ABS
[MWRB06] A. Münch, B. Wagner, M. Rauscher and R. Blossey.
A thin film model for corotational Jeffreys fluids under strong slip.
European Phys. J. E, 20(4):365-368 2006. 		PDF ABS
[PMN09] D. Peschka, A. Münch and B. Niethammer.
Thin film rupture for large slip.
J. Engrg. Math., 66(1):33-51, 2010. (Also WIAS preprint number 1417.) 		PDF ABS
[RBMW08] M. Rauscher, R. Blossey, A. Münch and B Wagner.
Spinodal dewetting of thin films with large interfacial slip: implications from the dispersion relation.
Langmuir, 24: 12290-12294, 2008. (Also WIAS preprint number 1380.) 		PDF ABS

Matheon first funding round

Submitted articles

First funding round: Submitted articles
[Mue04] A. Münch.
Fingering instability in dewetting films induced by slippage, 2004. 		PDF ABS
[WM04] B. Wagner and A. Münch.
Galerkin approximation for Rayleigh-Bénard convection.
Appeared in Nonlinearity (see above). (Also WIAS preprint number 907.) 		PDF ABS

Papers published in peer-reviewed journals

First funding round: Papers published in peer-reviewed journals
[ESR05] P. L. Evans, L. W. Schwartz and R. V. Roy.
Three-dimensional solutions for coating flow on a rotating horizontal cylinder: theory and experiment.
Phys. Fluids, 17(7):072102, 2005		 PDF ABS
[FJMWW05] R. Fetzer, K. Jacobs, A. Münch, B. Wagner, and T. P. Witelski.
New slip regimes and the shape of dewetting thin liquid films.
Phys. Rev. Lett., 95(12):127801, 2005.		 PDF ABS
[JAM05] B. Jin, A. Acrivos, and A. Münch.
The drag-out problem in film coating.
Phys. Fluids, 17:103603, 2005		 PDF ABS
[Mue05b] A. Münch.
Dewetting rates of thin liquid films.
Journal of Physics: Condensed Matter, 17:S309-S318, 2005.		 PDF ABS
[ME05] A. Münch and P. L. Evans.
Marangoni-driven liquid films rising out of a meniscus onto a nearly horizontal substrate.
Physica D, 209(1-4):164-177, 2005.		 PDF ABS
[MWW05] A. Münch, B. Wagner, and T. P. Witelski.
Lubrication models with small to large slip lengths.
J. Engrg. Math., 53(3-4):359-383, 2005. (Also WIAS preprint number 1069.) 		PDF ABS
[RMWB05] M. Rauscher, A. Münch, B. Wagner, and R. Blossey.
A thin-film equation for viscoelastic liquids of Jeffreys type.
European Phys. J. E - Soft Matter, 17:373-379, 2005.		 PDF ABS
[ESR04] P. L. Evans, L. W. Schwartz and R. V. Roy.
Steady and unsteady solutions for coating flow on a rotating horizontal cylinder: Two-dimensional theoretical and numerical modeling.
Phys. Fluids, 16(8): 2742-2756, 2004.		 PDF ABS
[MW04] A. Münch and B. Wagner.
Contact-line instability of dewetting thin films.
Physica D, 209(1-4):178-190, 2005.		 PDF ABS
[Mue03] A. Münch.
Pinch-off transition in Marangoni-driven thin films.
Phys. Rev. Lett., 91(1):016105, 2003.		 PDF ABS
[Mue02] A. Münch.
The thickness of a Marangoni-driven thin liquid film emerging from a meniscus.
SIAM J. Appl. Math, 62(6):2045-2063, 2002.		 PDF ABS
C10 project, Feb 2012