Wave propagation in porous and granular

[Next]:

Thermodynamic modeling of porous and granular

[Up]:

Project descriptions

[Previous]:

Stability and relaxation of flows in

[Contents]

[Index]

Wave propagation in porous and granular materials

Collaborator: K. Wilmanski , B. Albers

Cooperation with: I. Edelman (Alexander von Humboldt fellow in WIAS, Russian Academy of Sciences, Moscow), S. Foti, R. Lancellotta (Università di Torino, Italy), C. Lai (Studio Geotecnico Italiano, Milano)

Description: Aims and results of the project

The project is the continuation of the research devoted to a theoretical analysis of weak discontinuity waves on the basis of the own model (e.g., [1, 2]), as well as practical geotechnical applications particularly in a nondestructive testing of soils. Two main topics are in the process of investigation:

1.: Long-wave and low-frequency approximations of surface waves on the interface: vacuum/porous body;
2.: Gassmann relations and estimations of porosity by means of measurements of speeds of bulk waves.

It has been found out that results are different in the case when the problem of monochromatic waves is formulated in the space of real wave numbers, k (initial value problems), and in the case of real frequencies, $\omega$ (boundary value problems). For this reason a new asymptotic approximation has been developed by I. Edelman [3, 4, 5, 6]. She has shown that the P2 wave possesses a limit of the wave length beyond which this wave cannot propagate, i.e. the frequency becomes purely imaginary. The value of this limit depends on the bulk permeability coefficient. As the existence of Stoneley waves is coupled with the existence of P2 waves these waves possess a similar property. In the work [7] this property has been illustrated by a few numerical examples and compared with the properties of solutions for real $\omega$ .

In the subsequent works [8, 9] the properties of bulk and surface waves defined on the space of real $\omega$ have been investigated for the small frequency limit and it has been found out that the singularity discovered by Edelman does not exist in this formulation. The limits $\omega \rightarrow 0$ for P1 and S waves are regular and they give relations for the speeds of propagation:

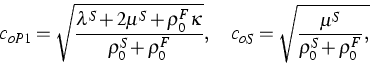
$\begin{displaymath} c_{oP1}=\sqrt{\frac{\lambda ^{S}+2\mu ^{S}+\rho _{0}^{F}\kap... ...uad c_{oS}=\sqrt{\frac{\mu ^{S}}{\rho _{0}^{S}+\rho _{0}^{F}},}\end{displaymath}$

where $\lambda ^{S},\mu ^{S},\kappa$ are Lamé constants and the compressibility of the fluid, respectively, while $\rho _{0}^{S},\rho _{0}^{F}$ are partial mass densities of the skeleton and of the fluid, respectively. These results agree with those of geophysicists. They show that the body reacts as if it was a composite of two elastic systems in a synchronized motion. Simultaneously, the limit for P2 waves is singular and it behaves as if the system were parabolic in connection with that mode which means that the speed limit of this wave goes to zero as $\sqrt{\omega}$ .

Similar asymptotic analysis shows that the speed of the Stoneley wave becomes zero as $\omega$ goes to zero. The Rayleigh wave satisfies the following relation for the speed of propagation

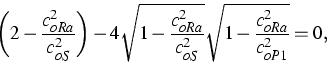
$\begin{displaymath} \left( 2-\frac{c_{oRa}^{2}}{c_{oS}^{2}}\right) -4\sqrt{1-\fr... ...}^{2}}{c_{oS}^{2}}}\sqrt{1-\frac{c_{oRa}^{2}}{c_{oP1}^{2}}}=0, \end{displaymath}$

which is identical with the classical Rayleigh equation except that speeds of bulk waves were replaced by the low-frequency limit counterparts.

The second topic arises in connection with a transition from microscopic to macroscopic relations for granular materials. As reported in the last year a nondestructive testing of soils by means of analysis of the field data for bulk and surface waves requires the transformation of microscopic compressibility properties into macroscopic parameters. This can be achieved by analysis of three simple tests:

jacketed drained gedankenexperiment (left figure with open tap);
jacketed undrained gedankenexperiment (left figure with closed tap);
unjacketed gedankenexperiment (right figure).

$\begin{figure} \makeatletter \@ZweiProjektbilderNocap[h]{0.4\textwidth}{jb1bildlinks.ps.gz}{jb1bildrechts.ps.gz} \makeatother\end{figure}$

All these tests must satisfy the following set of equations relating a macroscopic equilibrium state to a microscopic equilibrium state.

1.

Geometric compatibility:

$\begin{displaymath} e=n_{0}\varepsilon ^{R}+\left( 1-n_{0}\right) e^{R}, \end{displaymath}$

where $e,\varepsilon ^{R},e^{R}$ denote macroscopic volume changes of the skeleton, microscopic volume changes of the fluid and of the grains, respectively, and n₀ is the porosity.

2.

Dynamic compatibility:

$\begin{displaymath} p^{F}=n_{0}p^{FR},\quad p^{S}=\left( 1-n_{0}\right) p^{SR}, \end{displaymath}$

where p^F,p^S denote macroscopic partial pressures, p^FR is a pore pressure, and p^SR -- pressure in the grains.

3.

Constitutive relations:

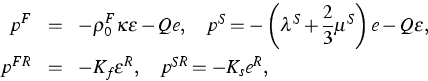
$\begin{eqnarray*} p^{F} &=&-\rho _{0}^{F}\kappa \varepsilon -Qe,\quad p^{S}=-\le... ...n , \ p^{FR} &=&-K_{f}\varepsilon ^{R},\quad p^{SR}=-K_{s}e^{R},\end{eqnarray*}$

where $\varepsilon$ is the macroscopic volume change of the fluid, K_f,K_s denote microscopic (real) compressibilities, and Q is a coupling constant.

4.

Equilibrium condition:

p=p^S+p^F,

where p is an external excess pressure.

The definitions of three gedankenexperiments lead to a system of equations which allows to determine the dependence of macroscopic parameters and microscopic parameters on porosity. These are the so-called Gassmann-type relations. Derivation of those relations shows that the method of micro-macro transition must be considerably improved in order to describe such properties of the porous material as a degree of saturation or capillarity effects. In spite of its flaws the above-described method yields results which agree quite well with the field experiments. This has been demonstrated in the works of the Italian partners of the project (e.g., [10]).

References:

K. WILMANSKI, On weak discontinuity waves in porous materials, in: Trends in Applications of Mathematics to Mechanics, M. Marques, J. Rodrigues, eds., Longman Scientific & Technical, Essex, 1995, pp. 71-83.
K. WILMANSKI, K. HUTTER, eds., Kinetic and Continuum Theories of Granular and Porous Media, vol. 400 of CISM Courses and Lectures, Springer, Wien, New York, 1999.
I. EDELMAN, On the bifurcation of the Biot slow wave in a porous medium, WIAS Preprint no. 738, 2002 .
$\dito$ , Asymptotic analysis of surface waves at vacuum/porous medium interface: Low-frequency range, WIAS Preprint no. 745, 2002 .
$\dito$ , On the velocity of the Biot slow wave in a porous medium: Uniform asymptotic expansion, WIAS Preprint no. 775, 2002 .
$\dito$ , Existence of the Stoneley surface wave at vacuum/porous medium interface: Low-frequency range, WIAS Preprint no. 789, 2002 .
K. WILMANSKI, Note on weak discontinuity waves in linear poroelastic materials. Part I: Acoustic waves in saturated porous media, WIAS Preprint no. 730, 2002 .
K. WILMANSKI, B. ALBERS, Acoustic waves in porous solid-fluid mixtures, to appear in: Deformation and Failure of Granular and Porous Continua, N. Kirchner, K. Hutter, eds., Lecture Notes in Applied Mechanics, Springer, Berlin.
B. ALBERS, K. WILMANSKI, Sound and surface waves in poroelastic media, WIAS Preprint no. 757, 2002 .
S. FOTI, C. LAI, R. LANCELLOTTA, Porosity of fluid-saturated porous media from measured seismic wave velocity, submitted.