[Next]:

Wave propagation in porous and granular

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index] 

Stability and relaxation of flows in porous materials

Collaborator: B. Albers

Cooperation with: B. Straughan (University of Durham, UK)

Description:

The aim of the project is the linear stability analysis of flow processes without and with mass exchange in porous media, especially in soils. Last year we reported already about the relaxation properties of a 1D flow disturbed by longitudinal (1D) disturbances. We have shown that the 1D steady state flow through a porous material is stable with respect to a linear longitudinal disturbance without and with mass exchange in the whole range of control permeability parameters $\pi$ and $\alpha$. These parameters are two important model parameters: the bulk permeability coefficient $\pi$, and the surface permeability $\alpha$. While the first one enters the field equations and describes the effective resistance of the skeleton to the flow of the fluid, the latter enters the model through the boundary conditions of the third type, and accounts for properties of the surface. It is one of the material parameters which determine the fluid velocity. Consequently the two important parameters control two competing mechanisms responsible for the stability of the flow.

This year we investigated another disturbance, namely a transversal (2D) disturbance of the 1D base flow following from the set of equations

$$\dfrac{\partial \rho ^{F}}{\partial t}+\dfrac{\partial \rho ... ...\partial p^{F}}{\partial x}-\pi v_{x}^{F},\hspace{1.5cm}0<x<l,$$

which are the mass and momentum balances of the fluid. Here, $\rho ^{F}$ is the mass density of the fluid component and v_x^F is the fluid velocity in x-direction. The partial pressure in the fluid is denoted by p^F. We investigate solely steady-state processes. Consequently the base flow does not contain any influence from mass exchange.

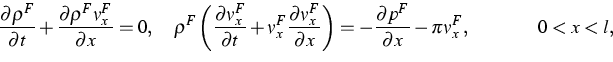
For the stability analysis a regular perturbation method is employed, but restricted to zeroth and first-order contributions. This means that the fields are viewed as a superposition of the base solution (indicated by 0) and a small perturbation (indicated by 1):

$$\begin{eqnarray*} & \rho ^{F}=\overset{0}{\rho }\left( x\right) +\varepsilon \ov... ...d v_{z}^{F}=\varepsilon \overset{1}{v}_{z}\left( x,z,t\right) . &\end{eqnarray*}$$

Here, c denotes the concentration of the adsorbate in the fluid component, $\xi$ is the fraction of occupied sites on the inner surface of the skeleton, and v_z^F is the velocity of the fluid/adsorbate mixture in z-direction. The disturbances follow in the first step of perturbation from the adsorption/diffusion model (see, e.g., [1])

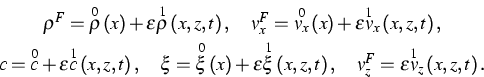
$$\begin{eqnarray*} & & \frac{\partial \rho ^{L}}{\partial t}+\rho ^{L}\left( \fra... ...L}}{p_{0}}\left( 1-\xi \right) -\xi \right] \frac{1}{\tau _{ad}},\end{eqnarray*}$$

$$\begin{eqnarray*} \rho ^{L}\left[ \frac{\partial v_{x}^{F}}{\partial t}+v_{x}^{F... ...z}\right] & = & -\frac{\partial p^{L}}{\partial z}-\pi v_{z}^{F}.\end{eqnarray*}$$

The following boundary conditions are assumed

$$\begin{array} {r} -\left. \rho ^{F}v_{x}^{F}\right\vert _{x=... ...t] ,\end{array}\qquad \left. v_{z}^{F}\right\vert _{z=\pm b}=0.$$

After insertion of a wave ansatz for the disturbances, the eigenvalue problem for $\omega$ is numerically solved by using a second-order finite difference scheme in an equidistant mesh. Results show that with respect to a transverse disturbance without mass exchange similarly to the 1D disturbance an instability does not appear, but for transverse disturbances with mass exchange there appears a region of parameters $\pi ,\alpha ,$ and $\rho _{ad}^{A}$ in which the base flow is unstable (see figure below). $\rho _{ad}^{A}$ is an additional parameter entering the model through the mass source: the mass density of the adsorbate on the internal surface. It is proportional to the size of the internal surface which plays an enormous role for the global rate and amount of adsorption. For different soils it may vary a few orders of magnitude.

Not only the distinction in 1D and 2D disturbances plays an important role, but also the comparison of results for disturbances without and with mass exchange is an important result of this work. While already for 1D disturbances adsorption decreases the maximum values of the real parts of $\omega$ by orders of magnitude, for the 2D disturbances it even decides whether the base flow is stable or unstable. For small values of $\pi$ the border of the instability region strongly varies with the surface permeability parameter $\alpha .$ On the side of large $\pi ,$ the unstable region is bounded from below by a single value of $\pi .$ For sufficiently small $\alpha$ and $\rho _{ad}^{A}$, the base flow is unconditionally stable.

References:

1. B. ALBERS, Relaxation analysis and linear stability vs. adsorption in porous materials, WIAS Preprint no. 721, 2002 , Contin. Mech. Thermodyn., Online: http://dx.doi.org/10.1007/s00161-002-0105-1, 2002.
2. , Linear stability analysis of a 1D flow in a poroelastic material under disturbances with adsorption, in: Proceedings of the 11th Conference ``Waves and Stability in Continuous Media'', Porto Ercole, Italy, June 3-9, R. Monaco, M.P. Bianchi, S. Rionero, eds., World Scientific, Singapore, 2002, pp. 1-7.
3. , Linear stability of a 1D flow in porous media under transversal disturbance with adsorption, Arch. Mech., 54 (2002), pp. 589-603.

[Next]:

Wave propagation in porous and granular

[Up]:

Project descriptions

[Previous]:

Project descriptions

 [Contents] 

 [Index]