Large-scale static and dynamic process simulation

[Next]:

Simulation of microwave and semiconductor laser

[Up]:

Project descriptions

[Previous]:

Two- and three-dimensional unsteady melt-flow simulation

[Contents]

[Index]

Large-scale static and dynamic process simulation

Collaborator: J. Borchardt , F. Grund , D. Horn

Cooperation with: D. Zeitz (Alstom (Switzerland) Ltd., Baden)

Supported by: Alstom (Switzerland) Ltd., Baden

Description:

The more and more integrated modeling in process engineering leads to large-scale problems in static and dynamic process simulation. The complex real-world process models used in this field usually depend on numerous parameters, are in general highly nonlinear and often involve discontinuities. Using concentrated physical models, high-dimensional systems of nonlinear and differential-algebraic equations (DAEs) have to be solved in static and dynamic process simulation, respectively. For that purpose robust and efficient numerical simulation tools are needed. They are urgently necessary to improve process design, analysis, as well as operation in process industries.

Fig. 1: Unit-oriented modular model of a gas turbine
(ALSTOM (Switzerland) Ltd.)
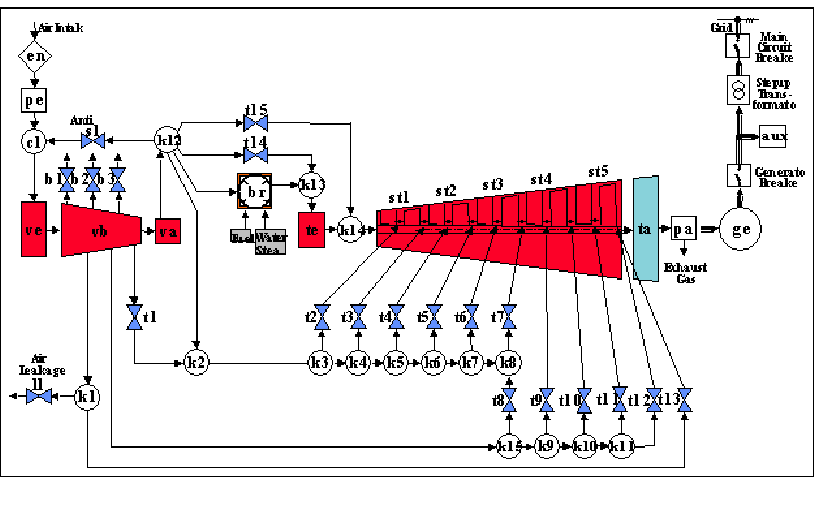
$\ProjektEPSbildNocap {0.92\textwidth}{alstom_slide2.eps.gz} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

The simulation concept developed at WIAS is based on divide-and-conquer techniques and exploits the modular structure of the process, which in most cases is defined by the hierarchical unit structure of the underlying plant (see, e.g., Figure 1). With it the corresponding system of equations is structured into subsystems according to the units and can be partitioned into blocks, which can then be treated almost concurrently within appropriately modified numerical methods. The approach has been implemented in the Block Oriented Process simulator BOP that uses an own compiler to generate a hierarchically structured data interface from a process description with its modeling language MLPE (Modeling Language for Process Engineering).

In the period under report, the homogeneous hierarchical simulation approach of BOP has been extended from chemical engineering to more general process engineering problems, and a steady-state solver for static process simulation problems has been added. Within this approach a block-partitioned system of equations

$\begin{eqnarray*} F_j(t,Y_j(t),\dot{Y}_j(t),U_j(t),\dot{U}_j(t),u(t)) = 0, ~~j=1(1)p,\end{eqnarray*}$

$\begin{displaymath} F_j : \mathbb{R}\times\mathbb{R}^{m_j}\times\mathbb{R}^{m_... ...hbb{R}^{m_j}, ~~~\sum_{i=1}^{p}m_j=n, ~~~t \in [t_0,t_{end}] \end{displaymath}$

has to be solved, where the vectors Y_j(t) and U_j(t) denote the unknown and coupling variables of the blocks, respectively, and u(t) the parameter functions. For static problems the system of DAEs degenerates to a system of nonlinear equations. Efficiently parallelizable block-structured Newton-type methods [2] can be applied in both cases. While these methods have shown to be successful in the dynamic simulation mode [1], a completely new static simulation mode based on these methods has now been added to the simulator. It combines the well-known globalized Newton method with block-structured Newton-type techniques and some special features resulting from real-world process engineering. The new steady-state solver within BOP has shown first promising results in industrial applications of gas turbine process engineering.

The numerical methods realized within BOP require a repeated solution of linear systems with the same pattern structure of sparse, unsymmetric coefficient matrices. Our direct solver GSPAR solves these linear systems by using advanced direct methods based on Gaussian elimination. Within this approach a new dynamic column reordering algorithm is used to minimize the number of fill-ins, and a modified partial pivoting technique maintains the numerical stability of the method.

GSPAR2 WSMP V1.7

First Fac- Second Fac- Analy- Factori-

Matrix N NNZ Condition torization torization sis zation

bayer01

lhr34c

circuit_4

shermanACb

57 735

35 152

80 209

18 510

277 774

764 014

307 604

145 149

4.4* 10¹⁵

4.5* 10⁹

4.7* 10⁹

2.6* 10⁶

0.840

6.260

1.430

3.020

0.160

1.460

0.050

0.730

2.640

2.710

1.980

0.460

0.460

0.470

0.300

0.110

This modified approach has been implemented in our new linear solver GSPAR2. It has been compared with the solver WSMP (Watson Sparse Matrix Packages) (Anshul Gupta, IBM Research Division, Yorktown Heights, New York, USA) concerning computing time. The results for linear systems with matrices arising from different real-world applications are given in Table 1. Here N denotes the order and NNZ the number of nonzeros of the matrices. The computations have been performed on an IBM 7040-681, pSeries 690 with 64-bit Power4 processors.

We have both ported the simulator BOP to PCs operating under Windows 2000 and realized some extensions in the process description. In particular, the process description language MLPE has been expanded with a so-called global section, which allows to identify variables of different units and to define global constraint equations. Additionally, the implementation of a subset of the language of the Aspen Custom Modeler^TM has been started.

References:

J. BORCHARDT, Newton-type decomposition methods in parallel process simulation of chemical plants, AIDIC Conference Series, 5 (2002), pp. 57-64.
$\dito$ , Newton-type decomposition methods in large-scale dynamic process simulation, Computers and Chemical Engineering, 25 (2001), pp. 951-961.
F. GRUND, K. EHRHARDT, J. BORCHARDT, D. HORN, Heterogeneous dynamic process flowsheet simulation of chemical plants, to appear in: Mathematics -- Key Technology for the Future II, K.-H. Hoffmann, W. Jäger, T. Lohmann, H. Schunck, eds., Springer, Berlin.