[Next]:

Large-scale static and dynamic process simulation

[Up]:

Project descriptions

[Previous]:

Finite element methods for surface diffusion

 [Contents] 

 [Index] 

Two- and three-dimensional unsteady melt-flow simulation in Czochralski crystal growth

Collaborator: E. Bänsch , D. Davis , H. Langmach , G. Reinhardt , N. Scurtu , M. Uhle

Cooperation with: K. Böttcher, W. Miller, U. Rehse (Institut für Kristallzüchtung (IKZ), Berlin)

Description: Semiconductor single crystals and their properties are of central importance in the fields of computer technology and communication. An important application is the production of large crystals with homogeneous and low defect concentration. A well-established processing technique for this purpose is the vapor-pressure-controlled Czochralski method, which is used extensively at IKZ to grow gallium arsenide (GaAs) crystals. This method is characterized by crystal extraction from a crucible containing semiconductor (GaAs) melt, with a viscous encapsulant of relatively large Prandtl number surrounding the crystal and melt, and serving to minimize heat loss. The crucible is heated from the side and below, thereby provoking heat and mass transfer within the melt, and reducing the impurities therein. Furthermore, the crystal and the crucible are rotated since this can directly influence the shape of the liquid-solid interface at the crystal/melt surface, as has been demonstrated at IKZ; in particular, it has been shown that a desired convex interface is best achieved through iso-rotation, i.e. with the crystal and crucible rotated in the same direction.

The liquid mechanics are governed by the Navier-Stokes equations with Boussinesq approximation, together with equations for mass conservation and heat transport (and relevant boundary and initial conditions), i.e.

Navier-Stokes-Boussinesq equations

$$\partial_t \vec{u} + \vec{u}\cdot\nabla\vec{u} -\frac{1}{Re... ...c{Gr}{Re^2}T\nabla x_3 \quad\mbox{in $\Omega\times[t_0,t_1]$};$$

continuity equation

$$\nabla\cdot\vec{u}=0 \quad\mbox{in $\Omega\times[t_0,t_1]$};$$

heat transport equation

$$\partial_t T + \vec{u}\cdot\nabla T -\frac{1}{Re\;Pr}\Delta T = 0 \quad\mbox{in $\Omega\times[t_0,t_1]$}.$$

Here, $\vec{u}$, p, T denote the dimensionless velocity, pressure and temperature (zeroed on the crystal melt temperature), while Re, Pr and Gr denote the (rotational) Reynolds, Prandtl and Grashof numbers, in turn. Also, $\Omega$ is the melt zone, while [t₀, t₁] indicates an arbitrary time interval and x₃ is the axial coordinate.

There are three (disjoint) boundary sections: the crystal/melt interface ($\Gamma_X$), the encapsulant/melt interface ($\Gamma_E$) and the crucible surface ($\Gamma_C$) with $\partial\Omega = \Gamma_X\cup\Gamma_E\cup\Gamma_C$.The boundary conditions for the temperature play a pivotal rôle in determining the form of the flow and the thermal distribution within the melt. The simplest version of these is to impose a constant temperature on $\Gamma_C$(which naturally differs from the constant melt value imposed on $\Gamma_X$)together with an adiabatic condition on $\Gamma_E$. For the axisymmetric flow simulations, more realistic conditions for temperature, based on global temperature simulation results obtained at IKZ, have also been used, as described below. For the velocity, straightforward Dirichlet conditions, based on the rotational speeds of the crystal and crucible are used.

For this project, we have adapted our finite element code NAVIER for the simulation of the velocity field and the temperature distribution in the melt. This has been applied in a two-dimensional (2D) axisymmetric setting as well as for full three-dimensional (3D) flow simulations. The code uses Taylor-Hood elements (P², P¹) for the spatial discretization and a fractional-$\theta$ operator-splitting method for the temporal discretization. The numerical procedure, which favorably decouples the incompressibility condition from the treatment of the nonlinearity, is accurate and stable for a wide range of Reynolds numbers.

In simulating axisymmetric flows, we compared the time-averaged results of our unsteady simulations with results obtained at IKZ, where a commercial finite element program, simulating the quasi-stationary behavior of the flow, was employed. For moderate Reynolds numbers (up to 7500), excellent qualitative agreement has been obtained. Despite this, we generally observed the flow to be unsteady in nature, and hence, we believe that unsteady simulation is invaluable for a more precise understanding of the melt flow. Figure 1 shows a time-averaged result arising from the application of a linear temperature distribution on the crucible (with values 0.4, 1.0 and 0.9 at the lowest point, the junction of the curved and straight sections, and the highest point of the crucible, respectively, and interpolation with respect to the radial and axial coordinate on the curved and straight sections, in turn). Very similar qualitative solutions were obtained at critical locations in the melt zone (such as directly beneath the crystal) using constant temperature distributions on the crucible.

Fig. 1: Time-averaged results for axisymmetric flow simulation

In Figure 2, a time-history curve for the temperature at a given observation point (based on the linear temperature distribution) is shown. The given results were obtained using a rotation rate of 5 revolutions per minute, for both crystal and crucible, and furthermore the buoyancy parameter Gr/Re²=1.36, Pr=0.068 and Re=6365.

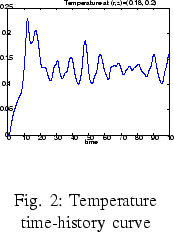For this given buoyancy parameter, axisymmetric computations performed in a cylindrical melt zone predict a switch from steady to unsteady motion at a critical Reynolds number $Re^* \approx 2200$.To allow for possible 3D flow structures beyond this critical value, the 3D version of NAVIER (applied to the same melt-zone geometry) has been implemented.

For weakly supercritical cases, the flow is initially dominated by a linear instability mode with azimuthal wave number 4, but eventually the flow becomes fully asymmetric due, we believe, to weakly-nonlinear growth effects leading to a modified (and fully 3D) basic flow.

Figure 3 depicts an asymmetric 3D flow for Reynolds number Re=2500 (with Gr/Re²=1.36). The corresponding time-averaged values can be seen in Figure 4. They suggest that for moderate Reynolds numbers, 2D effects still dominate over larger time scales, and moreover, that only negligible distortions of the temperature field are observed beneath the crystal.

Fig. 3: Asymmetric temperature distribution

Fig. 4: Time-average temperature distribution

Planned future work in cooperation with IKZ:

-

3D simulations using realistic geometry plus the influence of variable aspect ratio;

-

3D and 2D simulations for several regimes of buoyancy and rotation, especially for larger Reynolds numbers, that is O(10⁴);

-

2D simulations incorporating a model for the phase transition at the crystal/melt interface.

[Next]:

Large-scale static and dynamic process simulation

[Up]:

Project descriptions

[Previous]:

Finite element methods for surface diffusion

 [Contents] 

 [Index]