[Next]:  Multiscale systems  
 [Up]:  Project descriptions  
 [Previous]:  Project descriptions  
 [Contents]   [Index] 

Subsections

Dynamics of semiconductor lasers

Collaborator: M. Radziunas , K.R. Schneider , J. Sieber (until 9/02), D.V. Turaev , M. Wolfrum , S. Yanchuk (since 10/02)

Cooperation with: B. Sartorius, D. Hoffmann, H.-P. Nolting, O. Brox, S. Bauer (Heinrich-Hertz-Institut für Nachrichtentechnik, Berlin (HHI)), H.-J. Wünsche (Institut für Physik, Humboldt-Universität zu Berlin (HU)), L. Recke (Institut für Mathematik, Humboldt-Universität zu Berlin (HU)), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin (FBH)), M. Umbach (u2t Photonics AG, Berlin), U. Bandelow (WIAS: Research Group 1)

Supported by: BMBF: ``Hochfrequente Selbstpulsationen in Mehrsektions-Halbleiterlasern: Analysis, Simulation und Optimierung'' (High frequency self-pulsations in multi-section semiconductor lasers: Analysis, simulations, and optimization),

DFG: SFB 555 ``Komplexe Nichtlineare Prozesse''

(Collaborative Research Centre ``Complex Non-linear Processes''), DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien'' (DFG Research Center ``Mathematics for Key Technologies''),

Description:

Semiconductor laser devices play a key role in modern telecommunication systems for generating, transforming, and processing data at high speed. For optical networks they provide special components working in complicated nonlinear dynamical regimes (high frequency pulsations, synchronization, short pulses, fast switching).



Fig. 1: 3-section DFB laser for all optical clock recovery (Heinrich Hertz Institute, Berlin).
\ProjektEPSbildNocap {0.6\textwidth}{fig2_mr_1} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}

The mathematical research performed in this project includes

Project 1: Lasers with delayed and amplified delayed feedback.

Optical feedback is one of the main possibilities in a laser system to generate instabilities and complex dynamical phenomena. Based on the Lang-Kobayashi model

\begin{displaymath} \frac{dE}{dT}= \frac{1}{2}({\cal G}(N,\vert E(T)\vert^2) - ... ...}) \cdot E(T) + \kappa e^{-i\omega_0\tau_f} \cdot E(T-\tau_f),\end{displaymath}

\begin{displaymath} \frac{dN}{dT}=I - \frac{N}{\tau_c} - \mbox{Re}\left[ {\cal G}(N,\vert E(T)\vert^2) \right] \cdot \vert E(T)\vert^2,\end{displaymath}

a system of delay differential equations, we studied in [16] analytically the instabilities of lasers under the influence of moderate delayed feedback. A local center-manifold theorem has been proved in [14]. Using scaling methods, analytic expressions for different types of Hopf instabilities have been derived, leading to different types of pulsations of the laser. Moreover, the dependence of the pulsation frequency on the feedback parameters has been analyzed.

Based on this theoretical insight, a new device concept has been developed at the HHI: An additional amplifying section allows higher and tunable feedback strength. This lead to a new optical microwave source, the Amplified Feedback Laser, which is tunable from 10 to 40 GHz ([18]).

The main tuning (or bifurcation) parameters of this device are the current injection IA into the amplifier section and the current injection IP into the phase tuning section which is equivalent to the phase $\phi$ of the feedback.

In order to understand the dependence of the dynamics of the Amplified Feedback Laser on IA and $\phi$, a complete bifurcation analysis of the two-mode approximation ([19]) of the traveling wave equations ([1]) has been performed. Figure 2 reveals the regions of self-pulsations of different types and their borders in the parameter plane $\phi$-IA. A point of particular interest for applications is the widening of the region of mode-beating pulsations compared to the setup with passive feedback ([19]).


Fig. 2: Bifurcation diagram for the Amplified Feedback Laser in the parameter plane $\phi$-IA
\ProjektEPSbildNocap {0.6\textwidth}{fig2_js_1} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}

A further important dynamical regime occurring in lasers with delayed optical feedback is excitability. The theoretical background in the context of homoclinic bifurcations for excitability in different laser systems has been studied in [17]. Corresponding experimental results for the case of lasers with delayed feedback and corresponding numerical simulation results have been presented in [6].

Project 2: Software LDSL-tool.

The software LDSL-tool has been developed for the simulation and analysis of longitudinal dynamics in multisection semiconductor lasers. The underlying laser model is based on the traveling wave (TW) equations for the optical field propagating along the longitudinal axis of the laser ([1, 5]).

The agreement between simulations by LDSL-tool and experimental results is demonstrated in Figure 3 (see also [7, 8]), where the maximal field intensity of periodic solutions or stationary states in a 3-section DFB laser is represented in dependence on some parameter $\varphi$.Moreover, this figure can serve as an illustration of more advanced possibilities of LDSL-tool which are discussed below. Dashed brown and green lines show stable solutions observed in experiments (above) and in simulations of the TW model (below) for increasing and decreasing parameter $\varphi$.Solid red and blue lines show stable and unstable solutions of the system representing a two-mode approximation. Different bifurcations and regions where excitable behavior of a laser can be expected are indicated by thick symbols and yellow shading.



Fig. 3: Bifurcation diagrams
\ProjektEPSbildNocap {0.48\textwidth}{fig2_mr_2n.eps} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}

 
Fig. 4: A schema of LDSL-tool
\ProjektEPSbildNocap {0.48\textwidth}{fig2_mr_3n.eps} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}

The structure of LDSL-tool is discussed in [8, 10] and is represented by a brief schema in Figure 4. Here, blue, green and yellow boxes indicate the hierarchy of models, computational efforts and different data representation/processing procedures, respectively. Blue arrows show transitions which can be done only for some simplified models under some additional assumptions.

The potentialities of LDSL-tool are extended continuously. Besides of numerical integration of different TW models, LDSL-tool performs some post-processing procedures on the computed data stream ([5, 9]), solves spectral problems defining longitudinal modes of the optical field, and allows to study the dynamics of these modes ([3, 6]). Under some assumptions, the software can be used to perform model reductions, to integrate reduced mode approximation (MA) systems ([13]), and to compare their solutions with the solutions of the full TW model ([6, 8]). Moreover, a bifurcation analysis of MA systems allows to identify different types of the transition between dynamical regimes in the TW model [7]. After finding a good agreement between experiments and simulations by LDSL-tool (see [3, 5, 10] and comparing brown/green dashed lines in upper and lower diagrams of Figure 3), one is able not only to explain the origin of dynamics in the lasers (see bifurcations indicated in lower part of Figure 3), but also to predict some dynamical effects, such as excitable behavior of lasers (yellow shaded regions in Figure 3) realized later in experiments [4, 6].

At present, the software is successfully used by coworkers of the Department of Physics of the Humboldt University, of the Heinrich Hertz Institute, and of the Ferdinand Braun Institute to simulate and to analyze the behavior of different lasers. In particular, LDSL-tool is applied to study excitability in lasers with short external cavity ([4, 6]), self-pulsations in lasers with amplified feedback ([11, 12]), in DFB lasers with dispersive feedback ([1, 5, 7]), in lasers with two active DFB sections ([3, 9, 10]), and high power pulse generation in DBR lasers ([15]).

Project 3: Research of effects degrading high-frequency self-pulsations.

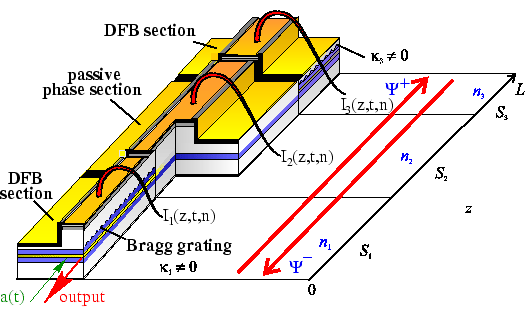
In the frame of the BMBF project ``Hochfrequente Selbstpulsationen in Mehrsektions-Halbleiterlasern: Analysis, Simulation und Optimierung'' (High-frequency self-pulsations in multi-section semiconductor lasers: Analysis, simulations, and optimization), in cooperation with the Heinrich Hertz Institute, Berlin, and the company u2t Photonics, Berlin, the behavior of a three-section laser with two active DFB sections (see Figure 1) has been investigated.

It was demonstrated experimentally and theoretically ([3]) that such a laser can operate at high frequency ($\sim$20-160 GHz) self-pulsations (SP) due to mutual action of two modes. Nevertheless, only some of the produced nominally identical devices could operate at the required pair of modes. The identification of possible reasons for this failure is one of the most important tasks in this project. By extensive numerical simulations of the impact of several possible limiting effects it was possible to avoid a lot of time-consuming and expensive experiments and measurements.

Finally, in [10] we have suggested that such problems can arise due to non-vanishing reflectivities for the counter-propagating fields at the junctions of the laser sections S1/S2 and S2/S3. Since the phases of the complex reflectivity coefficients r1 and r2 can not be controlled during the production of the devices, it is important to estimate the reflectivity amplitudes |r1,2| permitting the same type of SP for any phase of reflectivity in order to find conditions which guarantee a robust behavior under the requirements of the production process.


Fig. 5: Dependence of SP frequency on two internal reflectivity coefficients r1 and r2 at two slightly different operating conditions of self-pulsating laser
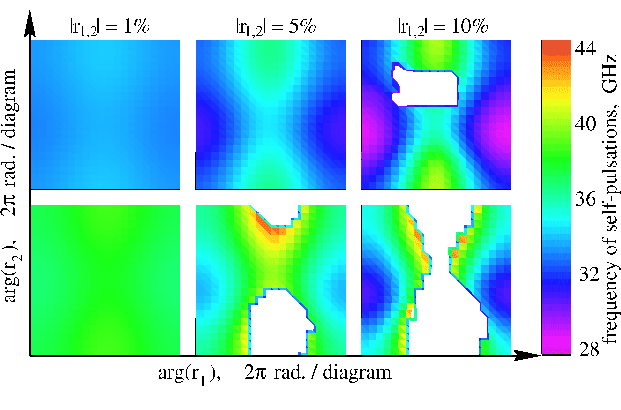
\ProjektEPSbildNocap {0.7\textwidth}{fig2_mr_4n.eps.gz} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}

The diagrams in Figure 5 represent a study of the effect of internal reflectivity on two slightly different self-pulsations at 33.5 and 38 GHz frequency. The SP represented in the upper diagrams are chosen from the middle of the area of similar self-pulsations in the parameter space, while the lower diagrams indicate similar SP closer to the border of the same area. In both cases we have applied the same reflectivity amplitudes for both of the junctions (fixing them at 1, 5, and 10 $\%$reflectivity) and have varied the reflectivity phases.

The white areas within the colored diagrams indicate totally different operational regimes. Therefore, 5 $\%$ amplitude reflectivity (which, actually, was present in the lasers made at the Heinrich Hertz Institute) do not degrade self-pulsations dramatically if we are in the middle of the SP area in the parameter plane, but can cause trouble if we are operating close to the border of the same area.

These simulations have shown the importance of a control of internal reflectivities. Our partners now are producing a new generation of multi-section lasers with reduced level of reflectivities.

References:

  1. U. BANDELOW, M. RADZIUNAS, J. SIEBER, M. WOLFRUM, Impact of gain dispersion on the spatio-temporal dynamics of multi-section lasers, WIAS Preprint no. 597 , 2000, IEEE J. Quantum Electron., 37 (2001), pp. 183-189.
  2. U. BANDELOW, H. WENZEL, H.-J. WÜNSCHE, Influence of inhomogeneous injection on sidemode suppression in strongly coupled DFB semiconductor lasers, Electronics Letters, 28 (1992), pp. 1324-1326.
  3. M. MÖHRLE, B. SARTORIUS, C. BORNHOLDT, S. BAUER, O. BROX, A. SIGMUND, R. STEINGRÜBER, M. RADZIUNAS, H.-J. WÜNSCHE, Detuned grating multi-section-RW-DFB lasers for high speed optical signal processing, IEEE J. Selected Topics Quantum Electron., 7 (2001), pp. 217-223.
  4. H.-J. W¨UNSCHE, O. BROX, M. RADZIUNAS, F. HENNEBERGER, Excitability of a semiconductor laser by a two-mode homoclinic bifurcation, Phys. Rev. Lett., 88 (2002), pp. 023901/1-023901/4.
  5. M. RADZIUNAS, H.-J. WÜNSCHE, B. SARTORIUS, O. BROX, D. HOFFMANN, K.R. SCHNEIDER, D. MARCENAC, Modeling self-pulsating DFB lasers with an integrated phase tuning section, WIAS Preprint no. 516 , 1999, IEEE J. Quantum Electron., 36 (2000), pp. 1026-1034.
  6. M. RADZIUNAS, H.-J. WÜNSCHE, O. BROX, F. HENNEBERGER, Excitability of a DFB laser with short external cavity, WIAS Preprint no. 712 , 2002, SPIE Proceedings Series, 4646 (2002), pp. 420-428.
  7. M. RADZIUNAS, H.-J. WÜNSCHE, Dynamics of multi-section DFB semiconductor laser: Traveling wave and mode approximation models, WIAS Preprint no. 713 , 2002, SPIE Proceedings Series, 4646 (2002), pp. 27-37.
  8. M. RADZIUNAS, H.-J. WÜNSCHE, LDSL-tool: A tool for simulation and analysis of longitudinal dynamics in multisection semiconductor laser, in: Proceedings of NUSOD-02, 2002, pp. 26-27.
  9. M. RADZIUNAS, Sampling techniques applicable for the characterization of the quality of self-pulsations in semiconductor lasers, WIAS Technical Report no. 2, 2002.
  10. M. RADZIUNAS, H.-J. WÜNSCHE, B. SARTORIUS, Simulation of phase-controlled mode-beating lasers, submitted.
  11. S. BAUER, O. BROX, J. KREISSL, G. SAHIN, B. SARTORIUS, Optical microwave source, Electronic Letters, 38 (2002), pp. 334-335.
  12. O. BROX, S. BAUER, M. RADZIUNAS, M. WOLFRUM, J. SIEBER, J. KREISSL, B. SARTORIUS, H.-J. W¨UNSCHE, High-frequency pulsations in DFB lasers with amplified feedback, submitted.
  13. J. SIEBER, Longitudinal dynamics of semiconductor lasers, PhD thesis, Humboldt-Universität zu Berlin, WIAS Report no. 20, 2001.
  14. \dito , Numerical bifurcation analysis for multi-section semiconductor lasers, WIAS Preprint no. 683 , 2001, SIAM J. Appl. Dyn. Syst., 1 (2002), pp. 248-270.
  15. K.-H. HASLER, H. WENZEL, A. KLEHR, G. ERBERT, Simulation of the generation of high-power pulses in the GHz range with three-section DBR lasers, IEE Proceedings Optoelectronic, Special Issue on Simulation of Semiconductor Optoelectronic Devices, 149 (2002), pp. 152-160.
  16. D. TURAEV, M. WOLFRUM, Instabilities of lasers with moderately delayed optical feedback, Optics Communications, 212 (2002), pp. 127-138.
  17. B. KRAUSKOPF, K.R. SCHNEIDER, J. SIEBER, S. WIECZOREK, M. WOLFRUM, Excitability and self-pulsations near homoclinic bifurcations in semiconductor laser systems, Optics Communications, 215 (2003), pp. 367-379.
  18. S. BAUER, O. BROX, J. SIEBER, M. WOLFRUM, Novel concept for a tunable optical microwave source, in: Proc. Conf. Optical Fiber Communication, Anaheim (USA), 2002, pp. ThM5.I158.
  19. J. SIEBER, Longtime behavior of the traveling-wave model for semiconductor lasers, WIAS Preprint no. 743 , 2002, to appear in: SIAM J. Appl. Dyn. Syst.


 [Next]:  Multiscale systems  
 [Up]:  Project descriptions  
 [Previous]:  Project descriptions  
 [Contents]   [Index] 

LaTeX typesetting by I. Bremer
5/16/2003